Cross Products

Sometimes people don’t want to hear the truth because they don’t want their illusions destroyed, the truth is too hard to bear, they don’t have the time or just don’t care or some unfathomable combination of the above, JustToThePoint, Anawim, #justtothepoint.

Recall

Definition. A vector $\vec{AB}$ is a geometric object or quantity that has both magnitude (or length) and direction. Vectors in an n-dimensional Euclidean space can be represented as coordinates vectors in a Cartesian coordinate system.

Definition. The magnitude of the vector $\vec{A}$, also known as length or norm, is given by the square root of the sum of its components squared, $|\vec{A}|~ or~ ||\vec{A}|| = \sqrt{a_1^2+a_2^2+a_3^2}$, e.g., $||< 3, 2, 1 >|| = \sqrt{3^2+2^2+1^2}=\sqrt{14}$, $||< 3, -4, 5 >|| = \sqrt{3^2+(-4)^2+5^2}=\sqrt{50}=5\sqrt{2}$, or $||< 1, 0, 0 >|| = \sqrt{1^2+0^2+0^2}=\sqrt{1}=1$.

• The sum of two vectors is the sum of their components, $\vec{A}+ \vec{B} = (a_1+b_1)\vec{i}+(a_2+b_2)\vec{j}+(a_3+b_3)\vec{k}$ = < (a₁+b₁), (a₂+b₂), (a₃+b₃) >.

• The subtraction of two vectors is similar to addition and is also done component-wise, it is given by simply subtracting their corresponding components (x, y, and z in 3D), $\vec{A} - \vec{B} = (a_1-b_1)\vec{i}+(a_2-b_2)\vec{j}+(a_3-b_3)\vec{k}$ = < (a₁-b₁), (a₂-b₂), (a₃-b₃) >.

• Scalar multiplication is the multiplication of a vector by a scalar, a real number, changing its magnitude without altering its direction. It is effectively multiplying each component of the vector by the scalar value, $c\vec{A} = (ca_1)\vec{i}+(ca_2)\vec{j}+(ca_3)\vec{k} = < ca_1, ca_2, ca_3>$.

• The dot or scalar product is a fundamental operation between two vectors. It produces a scalar quantity that represents the projection of one vector onto another. The dot product is the sum of the products of their corresponding components: $\vec{A}·\vec{B} = \sum a_ib_i = a_1b_1 + a_2b_2 + a_3b_3.$, e.g. $\vec{A}·\vec{B} = \sum a_ib_i = ⟨2, 2, -1⟩·⟨5, -3, 2⟩ = a_1b_1 + a_2b_2 + a_3b_3 = 2·5+2·(-3)+(-1)·2 = 10-6-2 = 2.$

It is the product of their magnitudes multiplied by the cosine of the angle between them, $\vec{A}·\vec{B}=||\vec{A}||·||\vec{B}||·cos(θ).$

Determinant in space

Let $\vec{A}, \vec{B},~\text{and} \vec{C}$ be three vectors in ℝ³ with components,

$\vec{A} = (\begin{smallmatrix}a_1\\a_2\\a_3\end{smallmatrix}), \vec{B} = (\begin{smallmatrix}b_1\\b_2\\b_3\end{smallmatrix}), \vec{C} = (\begin{smallmatrix}c_1\\c_2\\c_3\end{smallmatrix})$.

The determinant of the matrix formed by these three vectors, denoted as $det(\vec{A}, \vec{B}, \vec{C})$, is given by

$det(\vec{A}, \vec{B}, \vec{C}) = |\begin{smallmatrix}a_1 & a_2 & a_3\\ b_1 & b_2 & b_3\\ c_1 & c_2 & c_3\end{smallmatrix}| = a_1det(\begin{smallmatrix}b_2 & b_3\\ c_2 & c_3\end{smallmatrix})-a_2det(\begin{smallmatrix}b_1 & b_3\\ c_1 & c_3\end{smallmatrix})+a_3det(\begin{smallmatrix}b_1 & b_2\\ c_1 & c_2\end{smallmatrix})$

Where the 2 × 2 determinants (also called minors) are calculated as follows:

$det(\begin{smallmatrix}b_2 & b_3\\ c_2 & c_3\end{smallmatrix}) = b_2c_3-b_3c_2, det(\begin{smallmatrix}b_1 & b_3\\ c_1 & c_3\end{smallmatrix}) = b_1c_3 -b_3c_1, det(\begin{smallmatrix}b_1 & b_2\\ c_1 & c_2\end{smallmatrix})=b_1c_2-b_2c_1$

In conclusion, $det(\vec{A}, \vec{B}, \vec{C}) = a_1(b_2c_3-b_3c_2) -a_2(b_1c_3 -b_3c_1) + a_3(b_1c_2-b_2c_1)$

Geometric Interpretation

Geometrically, the determinant $det(\vec{A}, \vec{B}, \vec{C})$ represents the volume of the parallelepiped spanned or formed by the vectors $\vec{A}, \vec{B},and~ \vec{C}$ (Figure ii). The sign of the determinant indicates the orientation of the three vectors. If the determinant is positive, the vectors form a right-handed system (if when you extend the fingers of your right hand along the direction of vector $\vec{A}$ and close them (middle finger) in the direction of $\vec{B}$, the thumb points roughly in the direction of $\vec{C}$); if negative, they form a left-handed system, e.g., $\vec{i}, \vec{j}, \vec{k}$ form a right handed system.

Cross Product

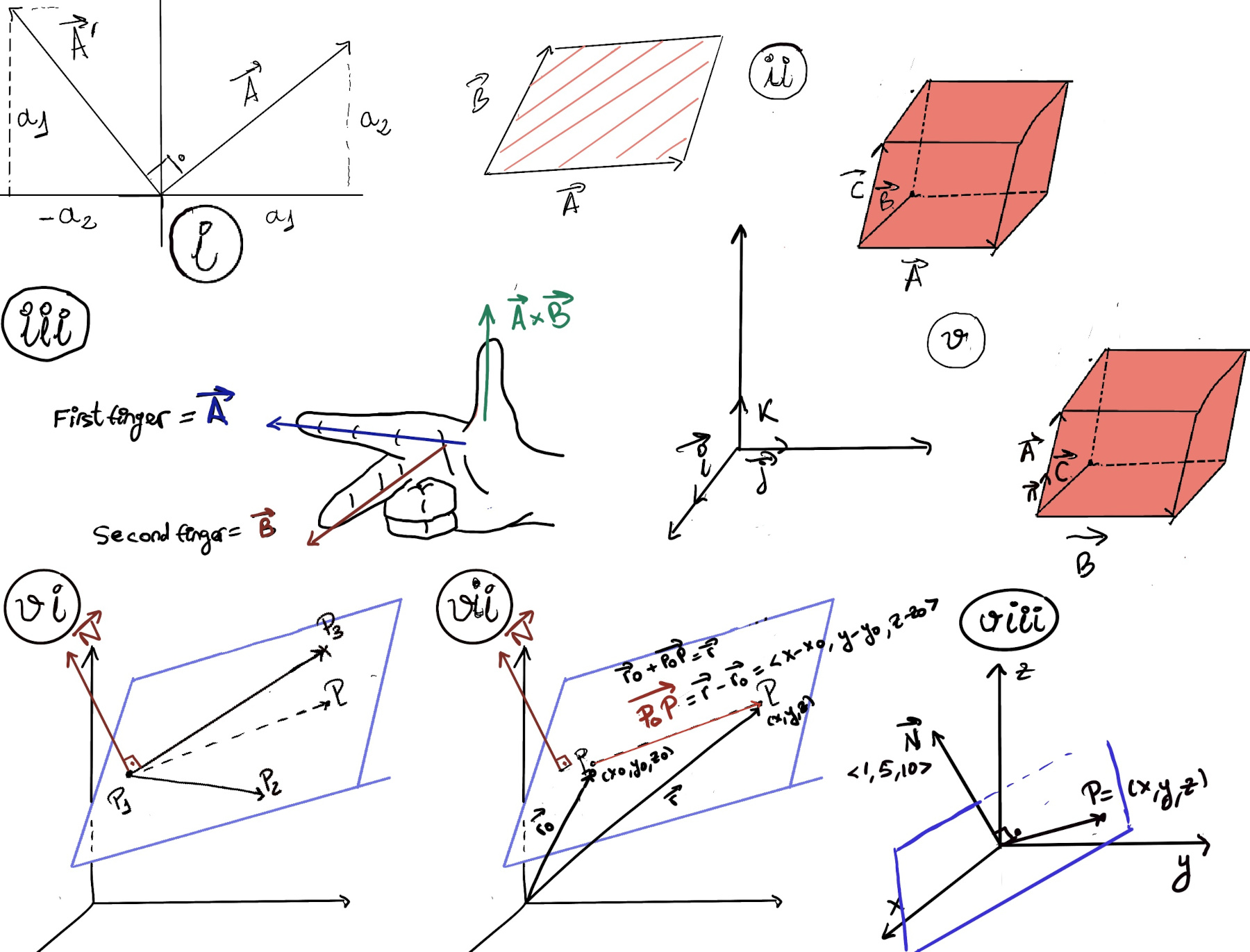
Definition. The cross product, denoted by $\vec{A}x\vec{B}$, is a binary operation on two vectors in three-dimensional space. It results in a vector that is perpendicular to both of the input vectors and has a magnitude equal to the area of the parallelogram formed by the two input vectors.

The direction of the resulting vector is determined by the right-hand rule: if you curl the fingers of your right hand from $\vec{A}$ to $\vec{B}$ (first finger points in the direction of $\vec{A}$, second finger points to $\vec{B}$), your thumb points in the direction of $\vec{A} \times \vec{B}$ (Figure iii).

The cross product $\vec{A}x\vec{B}$ can be computed using the following formula,

$\vec{A}x\vec{B} = det(\begin{smallmatrix}i & j & k\\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3\end{smallmatrix}) =|\begin{smallmatrix}a_2 & a_3\\ b_2 & b_3\end{smallmatrix}|\vec{i}-|\begin{smallmatrix}a_1 & a_3\\ b_1 & b_3\end{smallmatrix}|\vec{j}+|\begin{smallmatrix}a_1 & a_2\\ b_1 & b_2\end{smallmatrix}|\vec{k}$

Where the 2×2 determinants (minors) are calculated as follows:

$|\begin{smallmatrix}a_2 & a_3\\ b_2 & b_3\end{smallmatrix}| = a_2b_3-a_3b_2, |\begin{smallmatrix}a_1 & a_3\\ b_1 & b_3\end{smallmatrix}| = a_1b_3-a_3b_1, |\begin{smallmatrix}a_1 & a_2\\ b_1 & b_2\end{smallmatrix}| = a_1b_2-a_2b_1.$

In conclusion, $\vec{A}x\vec{B} = (a_2b_3-a_3b_2)\vec{i}-(a_1b_3-a_3b_1)\vec{j}+(a_1b_2-a_2b_1)\vec{k}$

Examples

• $\vec{i}x\vec{j} = det(\begin{smallmatrix}i & j & k\\ 1 & 0 & 0\\ 0 & 1 & 0\end{smallmatrix}) = (0·0-0·1)\vec{i}-(1·0-0·0)\vec{j}+(1·1-0·0)\vec{k} = \vec{k}$

• $⟨1,0,2⟩x⟨−1,−2,4⟩ = det(\begin{smallmatrix}i & j & k\\ 1 & 0 & 2 \\ -1 & -2 & 4\end{smallmatrix})=4\vec{i}-6\vec{j}+-2\vec{k}=⟨4, -6, -2⟩$.

• $⟨−2,1,3⟩x⟨5,2,−1⟩ = det(\begin{smallmatrix}i & j & k\\ -2 & 1 & 3 \\ 5 & 2 & -1\end{smallmatrix})=-7\vec{i}+13\vec{j}+-9\vec{k}=⟨-7, 13, -9⟩$.

Another way of calculating the volume of a parallelepiped spanned by the vectors $\vec{A}, \vec{B},and~ \vec{C}$ (Figure v) is using the base times heigh formula. This can be expressed as:

Volume = $|\vec{B}x\vec{C}|(\vec{A}·\vec{n})$ where $\vec{n}$ is a unit vector perpendicular to the parallelogram formed by $\vec{B} ~\text{and}~ \vec{C}$:

$\vec{n} = \frac{\vec{B}x\vec{C}}{|\vec{B}x\vec{C}|}$

Volume = $|\vec{B}x\vec{C}|(\vec{A}·\frac{\vec{B}x\vec{C}}{|\vec{B}x\vec{C}|}) = \vec{A}·(\vec{B}x\vec{C}) = det(\vec{A},\vec{B},\vec{C})$  

Verification

To verify this, let’s look at the determinant form:

$det(\vec{A}, \vec{B}, \vec{C}) = |\begin{smallmatrix}a_1 & a_2 & a_3\\ b_1 & b_2 & b_3\\ c_1 & c_2 & c_3\end{smallmatrix}| = a_1|\begin{smallmatrix}b_2 & b_3\\ c_2 & c_3\end{smallmatrix}|-a_2|\begin{smallmatrix}b_1 & b_3\\ c_1 & c_3\end{smallmatrix}|+a_3|\begin{smallmatrix}b_1 & b_2\\ c_1 & c_2\end{smallmatrix}|$

Expanding $\vec{A}·(\vec{B}x\vec{C})$

$\vec{A}·(\vec{B}x\vec{C}) =\vec{A}·(|\begin{smallmatrix}b_2 & b_3\\ c_2 & c_3\end{smallmatrix}|\vec{i}-|\begin{smallmatrix}b_1 & b_3\\ c_1 & c_3\end{smallmatrix}|\vec{j}+|\begin{smallmatrix}b_1 & b_2\\ c_1 & c_2\end{smallmatrix}|\vec{k}) = a_1|\begin{smallmatrix}b_2 & b_3\\ c_2 & c_3\end{smallmatrix}|-a_2|\begin{smallmatrix}b_1 & b_3\\ c_1 & c_3\end{smallmatrix}|+a_3|\begin{smallmatrix}b_1 & b_2\\ c_1 & c_2\end{smallmatrix}|$ ∎

Properties of the Cross Product

Let $\vec{u}, \vec{v}$, and $\vec{w}$ be vectors in space, and let c be a scalar, the following statements hold true (Credits: The Cross Product -Mathematics Libre Texts),

1. Anticommutative property: $\vec{u}x\vec{v}=-(\vec{v}x\vec{u})$
2. Distributive property: $\vec{u}x(\vec{v}+\vec{w})=(\vec{u}x\vec{v})+(\vec{u}x\vec{w})$
3. Multiplication by a constant: $c(\vec{u}x\vec{v})=(c\vec{u})x\vec{v}=\vec{u}x(c\vec{v})$
4. Cross product of the zero vector: $\vec{u}x\vec{0} = \vec{0}x\vec{u} = \vec{0}$
5. Cross product of a vector with itself: $\vec{u}x\vec{u}=\vec{0}$
6. Triple scalar product: $\vec{u}·(\vec{v}x\vec{w})=(\vec{u}x\vec{v})·\vec{w}$
7. Triple cross product: $\vec{u}x(\vec{v}x\vec{w})=(\vec{u}·\vec{w})\vec{v}-(\vec{u}·\vec{v})\vec{w}$

Find the Equation of a Plane Given Three Points

To find the equation of a plane given three points P₁, P₂, and P₃ in the plane, we need to determine a condition that ensures a fourth point P lies in the same plane.

Consider the vectors $\vec{P_1P}, \vec{P_1P_2},and~ \vec{P_1P_3}$. For point P to be in the planed defined by P₁, P₂, and P₃, the parallelepiped spanned by these vectors must be flat. This condition is mathematically represented by the determinant being zero: (Figure vi) $det(\vec{P_1P}, \vec{P_1P_2},~ \vec{P_1P_3})$ = 0

Definition. A normal vector to a plane is a vector that is perpendicular to the plane., A normal vector is perpendicular (orthogonal) to every vector that lies in the plane.

An alternative way to find the equation of the plane is by using a normal vector. For point P to be in the plane, the vector $\vec{P_1P}$ must be perpendicular to the normal vector $\vec{N}$, $\vec{P_1P}⊥\vec{N}$ where $\vec{N}$ is a normal vector to our plane. This can be expressed as $\vec{P_1P}·\vec{N}=0$ [🚀]

Finding the Normal Vector

A normal vector $\vec{N}$ to the plane can be found using the cross product of the vectors $\vec{P_1P_2}$ and $\vec{P_1P_3}$: $\vec{N}=\vec{P_1P_2}x\vec{P_1P_3}$

Thus, the condition that the point P lies in the plane can be rewritten as:

$\vec{P_1P}·\vec{N}=0 [🚀] ⇒ \vec{P_1P}·(\vec{P_1P_2}x\vec{P_1P_3})=0$ (In the accompanying figure vi, the vectors and the plane can be visualized to better understand the geometric relationships and the conditions derived). This shows that the dot product of $\vec{P_1P}$ with the normal vector $\vec{N}$ must be zero for P to lie in the plane.

Solved exercises

• Determine the equation of the plane that contains the points P₁ = ⟨1, −2, 0⟩, P₂ = ⟨3, 1, 4⟩, and P₃ = ⟨0, -1, 2⟩.

Recall that if P₁ has coordinates (x₁, y₁, z₁) and P₂ has coordinates (x₂, y₂, z₂), then the componentes of $\vec{P_1P_2}$ are ⟨x₂-x₁, y₂-y₁, z₂-z₁⟩, i.e., we subtract the coordinates of P₁ from the coordinates of P₂.

$\vec{P_1P_2} = ⟨2, 3, 4⟩, \vec{P_1P_3} = ⟨-1, 1, 2⟩$

$\vec{N}=\vec{P_1P_2}x\vec{P_1P_3} = [\begin{smallmatrix}i & j & k\\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3\end{smallmatrix}] = [\begin{smallmatrix}i & j & k\\ 2 & 3 & 4\\ -1 & 1 & 2\end{smallmatrix}] = 2\vec{i}-8\vec{j}+5\vec{k}$

P is in the plane ↭ $\vec{P_1P}⊥\vec{N}$ where N is a normal vector to our plane ↭ $\vec{P_1P}·\vec{N}=⟨x-1, y+2, z-0⟩·2\vec{i}-8\vec{j}+5\vec{k} = (x-1)2-8(y+2)+5z = 0 ↭ 2x -2 -8y -16+5z = 0 ↭ 2x -8y +5z = 18$, and this is the equation of the plane.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus and Calculus 3e (Apex). Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.