Vectors

Irony is wasted on the stupid, Oscar Wilde.

I have yet to see any problem, however complicated, which, when looked at in the right way did not become still more complicated, Paul Anderson.

Definition. A vector $\vec{AB}$ is a geometric object or quantity that has both magnitude (or length) and direction. Vectors in an n-dimensional Euclidean space can be represented as coordinates vectors in a Cartesian coordinate system. In the context of mathematics, physics, and engineering, vectors are used to describe various physical quantities, such as force, velocity, acceleration, fluid flow, momentum, electric and magnetic fields, etc.

The point A from where the vector starts is called its initial point, and the point B where it ends is called its terminal point. The distance between initial and terminal points of a vector is called the magnitude of the vector, denoted as $|\vec{AB}|$ or $||\vec{AB}||$. The magnitude of a vector represents its size or length. The arrow indicates the direction of the vector, $\vec{AB}$ represents a vector that starts from point A and ends at point B.

Typically, the standard basis vectors are often denoted as $\vec{i},~\vec{j},~\vec{k}$, thus $\vec{A} = a_1\vec{i}+a_2\vec{j}+a_3\vec{k}$ = < a₁, a₂, a₃ > (Figure i). Each component of the vector corresponds to the magnitude of the vector in the respective direction. $\vec{A} = a_1\vec{i}+a_2\vec{j}+a_3\vec{k}$ represents a vector with components a₁, a₂, and a₃ along the x, y, and z axes respectively.

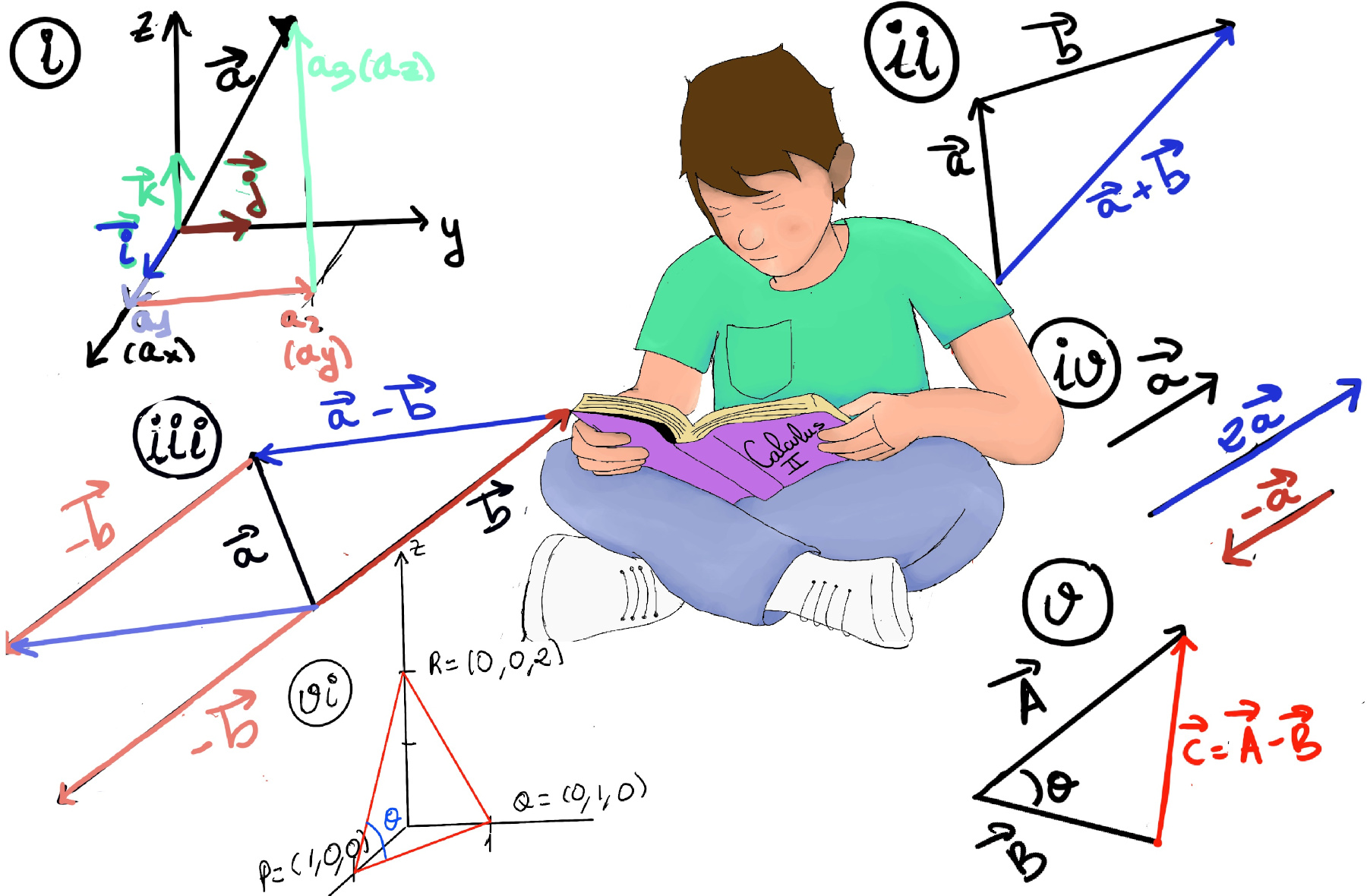  Definition. The magnitude of the vector $\vec{A}$, also known as length or norm, is given by the square root of the sum of its components squared, $|\vec{A}|~ or~ ||\vec{A}|| = \sqrt{a_1^2+a_2^2+a_3^2}$, e.g., $||< 3, 2, 1 >|| = \sqrt{3^2+2^2+1^2}=\sqrt{14}$, $||< 3, -4, 5 >|| = \sqrt{3^2+(-4)^2+5^2} = \sqrt{9+ 16 + 25} = \sqrt{50}=5\sqrt{2}$, or $||< 1, 0, 0 >|| = \sqrt{1^2+0^2+0^2}=\sqrt{1}=1$.

Definition. Any vector with magnitude of 1, i.e., $|\vec{A}|~ or~ ||\vec{A}|| = \sqrt{a_1^2+a_2^2+a_3^2} = 1$, is called a unit vector.

Vector Arithmetic

• The sum of two vectors is the sum of their components, $\vec{A}+ \vec{B} = (a_1+b_1)\vec{i}+(a_2+b_2)\vec{j}+(a_3+b_3)\vec{k}$ = < (a₁+b₁), (a₂+b₂), (a₃+b₃) >, e.g., $\vec{A}+\vec{B} = ⟨3, 2⟩ + ⟨5, 6⟩ = ⟨8, 8⟩, \vec{A}+\vec{B} = ⟨2,−1,3⟩ + ⟨−3,4,1⟩ = ⟨−1,3,4⟩, \vec{A}+\vec{B} = <3, 3, 3> + <1, 0, −1> = <4, 3, 2>$.

• The subtraction of two vectors is similar to addition and is also done component-wise, it is given by simply subtracting their corresponding components (x, y, and z in 3D), $\vec{A} - \vec{B} = (a_1-b_1)\vec{i}+(a_2-b_2)\vec{j}+(a_3-b_3)\vec{k}$ = < (a₁-b₁), (a₂-b₂), (a₃-b₃) >, e.g., $\vec{A}-\vec{B} = ⟨2,−1,3⟩ - ⟨−3,4,1⟩ = ⟨5, -5, 2⟩, \vec{A}-\vec{B} = ⟨6, -2, -5⟩ - ⟨-4, 7, -8⟩ = ⟨10, -9, 3⟩, \vec{B}-\vec{A} = ⟨-4, 7, -8⟩ - ⟨6, -2, -5⟩ = ⟨-10, 9, -3⟩.$

It may be represented graphically by placing the tail of the second vector $\vec{b}$ at the head of the first vector $\vec{a}$, and then drawing an arrow from the tail of the first vector to the head of the second. The new arrow drawn represents the vector $\vec{a+b}$ (Figure ii) and this is called the parallelogram rule because $\vec{a}$ and $\vec{b}$ form the sides of a parallelogram and $\vec{a+b}$ is one of the diagonals.

To subtract $\vec{B}$ from $\vec{A}$, place the tails of $\vec{A}$ and $\vec{B}$ at the same point, and then draw an arrow from the head of $\vec{B}$ to the head of $\vec{A}$ (Figure iii).

• Scalar multiplication is the multiplication of a vector by a scalar, a real number, changing its magnitude without altering its direction. It is effectively multiplying each component of the vector by the scalar value, $c\vec{A} = (ca_1)\vec{i}+(ca_2)\vec{j}+(ca_3)\vec{k} = < ca_1, ca_2, ca_3>$, e.g., $2\vec{A} = 2⟨3, 1, 1⟩ = ⟨6, 2, 2⟩; -3\vec{A} = -3⟨3, 2, -1⟩= (-9)\vec{i}+(-6)\vec{j}+(3)\vec{k} = < -9, -6, 3>$.

Intuitively, multiplying a vector by a scalar r stretches it out by a factor of r. Geometrically, this can be visualized as placing r copies of the vector in a line where the endpoint of one vector is the initial point of the next vector. If r is negative, then the vector changes direction or flips around (by an angle of 180°).

• Properties addition and scalar multiplication, ∀$\vec{v},\vec{u},\vec{w}$ vectors, ∀a, b ∈ ℝ:

1. Commutative property of vector addition, the order in which you add vectors does not matter, $\vec{v}+\vec{w}=\vec{w}+\vec{v}$.
2. Associative property of vector addition. It states that when adding three arbitrary vectors, the result is the same regardless of how the additions are grouped, $\vec{v}+(\vec{u}+\vec{w})=(\vec{v}+\vec{u})+\vec{w}$.
3. Additive Identity property. It states that adding the zero vector $\vec{0}$ to any vector $\vec{v}$, leaves the vector unchanged: $\vec{v}+\vec{0}=\vec{v}$.
4. Multiplicative Identity property. It states that multiplying a vector $\vec{v}$ by the scalar 1, leaves the vector unchanged, $1\vec{v} = \vec{v}$
5. Distributive property of scalar multiplication over vector addition. It states that multiplying a vector sum by a scalar is the same as multiplying each vector by the scalar and then adding the results, $a(\vec{v}+\vec{w})=a\vec{v}+a\vec{w}$.
6. Distributive property of scalar addition over vector multiplication. It states that multiplying a vector by the sum of two scalars is the same as multiplying the vector by each scalar separately and then adding the results, $(a+b)\vec{v} = a\vec{v}+b\vec{v}.$

• Dot product.

The dot or scalar product is a fundamental operation between two vectors. It produces a scalar quantity that represents the projection of one vector onto another. The dot product is the sum of the products of their corresponding components: $\vec{A}·\vec{B} = \sum a_ib_i = a_1b_1 + a_2b_2 + a_3b_3.$

Examples: $\vec{A}·\vec{B} = \sum a_ib_i = ⟨2, 2, -1⟩·⟨5, -3, 2⟩ = a_1b_1 + a_2b_2 + a_3b_3 = 2·5+2·(-3)+(-1)·2 = 10-6-2 = 2; \vec{A}·\vec{B} = ⟨3, 5, 2⟩·⟨-1, 3, 0⟩ = 3·(-1)+5·3+2·0 = -3 + 15 + 0 = 12, \vec{A}·\vec{B} = ⟨-3, 2, 2⟩·⟨-4, 2, 1⟩ = (−3)⋅(−4)+ 2⋅2 +2⋅1 = 12 + 4 + 2 = 18.$

Properties:

1. Distributive property of the dot product over vector addition. The dot product of a vector $\vec{u}$ with the sum of two vectors, say $\vec{v}$ and $\vec{w}$, is equal to the sum of the dot products of $\vec{u}$ with $\vec{v}$ and $\vec{w}$ individually: $\vec{u}·(\vec{v}+\vec{w})=\vec{u}·\vec{v}+\vec{u}·\vec{w}$
2. Scalar multiplication property. The dot product of a scalar multiple of a vector $\vec{v}$ with another vector $\vec{w}$ is equal to the scalar multiple of the dot product of $\vec{v}$ and $\vec{w}, (c\vec{v})·\vec{w} = \vec{v}·(c\vec{w})=c·(\vec{v}·\vec{w})$
3. Commutative property of the dot product, the order of the vectors does not affect the result, $\vec{v}·\vec{w}=\vec{w}·\vec{v}$.
4. Dot product of any vector with the zero vector is always zero, $\vec{u}·\vec{0} = 0$.
5. The dot product of a vector with itself is equal to the square of its magnitude, $\vec{u}·\vec{u}=|\vec{u}|^2.$
6. If the dot product of a vector with itself is zero, then the vector must be the zero vector. $\text{If}~ \vec{u}·\vec{u} = 0⇒ \vec{u} = \vec{0}$.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus and Calculus 3e (Apex). Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.