Vector fields in 3D

Mistakes are a great educator when one is honest enough to admit them and willing to learn from them, Aleksandr Solzhenitsynv.

Work hard in silence, let your success be your noise, Anonymous.

Vector fields in 3D

Scalar fields represent quantities such as temperature or pressure, while vector fields represent quantities with both magnitude and direction. Vector fields represent quantities (the electric field, fluid velocity, etc.) with both magnitude and direction that vary continuously throughout a three-dimensional space.

A vector field assigns a vector to each point in space, $\vec{F} = ⟨P, Q, R⟩$ where P, Q, and R are functions of the coordinates x, y, and z.

In Physics, a force field is a map of the force fell over a particular area of space. Examples are magnetic fields, electric fields, velocity fields, gradient fields, and gravitational fields.

The gravitational attraction is the attractive force that objects with mass exert on each other. Newton’s law of universal gravitation says that every particle (a small object with can be described by several properties such as volume, density, or mass) in the universe attracts every other particle in the universe with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.

It is expressed as $\vec{F} = -\frac{G·M·m}{r^2}\hat{\mathbf{r}}$ where G is the gravitational constant, M is the mass of the gravitating object (e.g., a planet, a comet, or a star), m is the mass of the object experiencing the gravitational force, r is the distance between the centers of mass of both objects, and $\hat{\mathbf{r}}$ is the unit vector pointing from the object experiencing the force to the gravitating object.

It can also be expressed as $|\vec{F}| ∝ \frac{c}{r^2}$ where $|\vec{F}|$ is the magnitude of the gravitational force, c is a constant representing the strength of the gravitational force and r is the distance between both objects.

In particular, the gravitational attraction of a solid mass m at the origin (0, 0, 0) on a mass M at (x, y, z), $\vec{F}$ is directed towards the origin and its magnitude $|\vec{F}| ∝ \frac{c}{ρ^2}$ (Figure A)

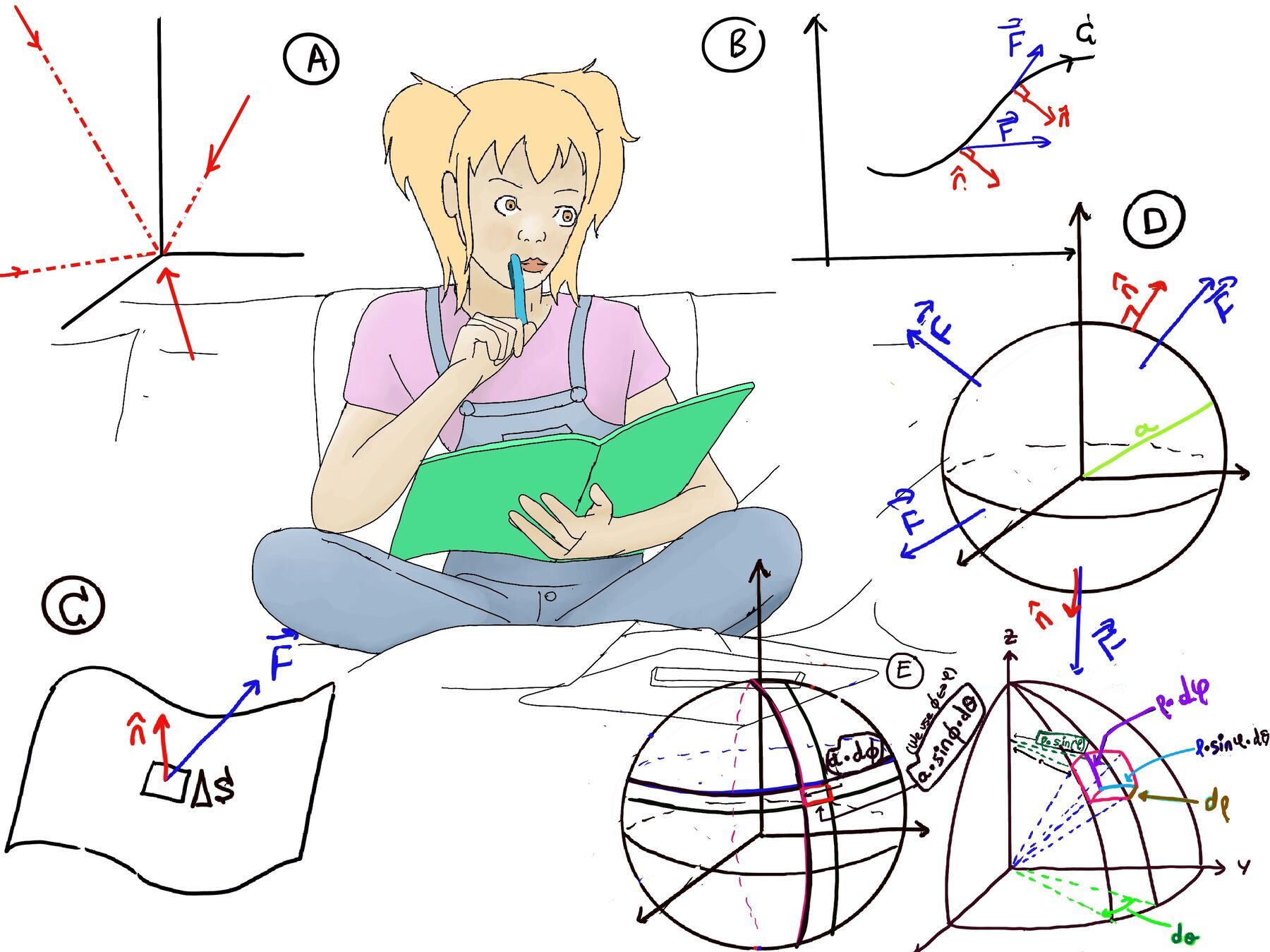
More specifically, $\vec{F} = \frac{-G·M·m⟨x, y, z⟩}{ρ^3} = \frac{-c⟨x, y, z⟩}{ρ^3}$ where we divide by ρ³ because we are taking into consideration the unit vector $\hat{\mathbf{r}} = \frac{⟨x, y, z⟩}{ρ}$ and c = G·M·m is considered a constant.

Recall that flux is another line integral, more precisely, the flux of a vector field $\vec{F}$ across a curve C is defined as the dot product of the vector field and the unit normal vector n to the surface S, that is, $\oint_{C} \vec{F}·\hat{\mathbf{n}}·ds$ where $\hat{\mathbf{n}}$ is the unit normal vector to the curve C (perpendicular to the curve and has length 1) pointing 90° in clockwise direction and ds represents an infinitesimal area element on the surface S (Figure B).

If $\vec{F}$ is a velocity field, it describes the velocity of a fluid (such as water) at every point in space and let’s say we have a surface S through which the fluid is flowing. We want to know how much fluid passes through S per unit time (Figure 5).

The way to see it is by taking a small area element dS and trying to figure out the stuff that flows per unit of time. The amount of fluid passing through dS per unit time is given by the velocity of the fluid at dS multiplied by the area of dS. $\vec{F}·\hat{\mathbf{n}}$ gives us the component of the vector field that is perpendicular to the surface. Multiplying this by the area of dS give us the volume of fluid passing through dS per unit time.

In the context of vector fields in space, flux will be a surface integral, not a line integral. It refers to how much my vector field is going across the surface.

Let’s say that we have a vector field $\vec{F}$ and a surface in space S and $\hat{\mathbf{n}}$ is the unit normal vector, Flux = $\oint_{S} \vec{F}·\hat{\mathbf{n}}·dS$ (Figure C) where dS stands for a surface area element and $d\vec{S} = \hat{\mathbf{n}}·dS$ is a vector which points perpendicular to the surface and whose length corresponds to the surface element.

The ease case is where the vector field is tangent to the surface, flux is zero.

• Let’s calculate the flux of $\vec{F} = ⟨x, y, z⟩$ (this vector field is pointing radially away from the origin) through a sphere of radius a located at the origin.

$\int \int_{S} \vec{F}·\hat{\mathbf{n}}·dS = \int \int_{S} \vec{F}· \vec{dS}$.

We can see (Figure D) that our normal vector and our vector field are parallel to each other.

$\hat{\mathbf{n}} = \frac{⟨x, y, z⟩}{|⟨x, y, z⟩|}$ =[Considering that we are in a sphere a = $\sqrt{x^2+y^2+z^2}$] $\frac{1}{a}·⟨x, y, z⟩$

$\vec{F}·\hat{\mathbf{n}} = |\vec{F}|·|\hat{\mathbf{n}}|·cos(0) = |\vec{F}|·1·1 = |\vec{F}| = a.$

Therefore, $\int \int_{S} \vec{F}·\hat{\mathbf{n}}·dS = \int \int_{S} adS = a\int \int_{S} dS = a ·area(S) = a·4πa^2 = 4πa^3$.

• Let’s calculate the flux of $\vec{F} = z\vec{k}$ through a sphere of radius a located at the origin.

Our previous argument, $\hat{\mathbf{n}} = \frac{⟨x, y, z⟩}{|⟨x, y, z⟩|}$ =[Considering that we are in a sphere a = $\sqrt{x^2+y^2+z^2}$] $\frac{1}{a}·⟨x, y, z⟩$ is still valid.

$\vec{F}·\hat{\mathbf{n}} = ⟨0, 0, z⟩·\frac{⟨x, y, z⟩}{a} = \frac{z^2}{a}$.

Therefore, $\int \int_{S} \vec{F}·\hat{\mathbf{n}}·dS = \int \int_{S} \frac{z^2}{a}·dS$

Using sphere coordinates (Figure E), dS = (adφ)·(a·sin(φ)·dθ) = a²sin(φ)dφdθ and we know that z = acos(φ)

$\int \int_{S} \frac{z^2}{a}·dS = \int_{0}^{2π} \int_{0}^{π} \frac{a^2cos^2(φ)}{a}a^2sin(φ)dφdθ = a^3\int_{0}^{2π} \int_{0}^{π} cos^2(φ)sin(φ)dφdθ =$

$\int_{0}^{π} cos^2(φ)sin(φ)dφ = -\frac{1}{3}cos^3(φ)\bigg|_{0}^{π} =\frac{2}{3}$

$\int \int_{S} \frac{z^2}{a}·dS = a^3\int_{0}^{2π} \frac{2}{3}dθ = \frac{a^3·2}{3}·θ\bigg|_{0}^{2π} = \frac{4}{3}πa^3.$

Let’s see some scenarios.

• We have a surface H that is an horizontal plane, say z = a (Figure 1), and $\hat{\mathbf{n}}$ the unit normal vector has two choices $\hat{\mathbf{n}} = ± \vec{k}$ and dS = dx·dy.

• We may have a vertical plane parallel to yz-plane, say x = a (Figure 2), and $\hat{\mathbf{n}}$ the unit normal vector has two choices $\hat{\mathbf{n}} = ± \vec{i}$ and dS = dy·dz.

• If we have as a surface a sphere of radius a centered at the origin, we have already computed that $\hat{\mathbf{n}} = ± \frac{⟨x, y, z⟩}{a}$ and dS = a²sin(φ)dφdθ

• If we have as a surface a cylinder of radius a centered at the z-axis (Figure 3, 3b), the unit normal vector has two choices $\hat{\mathbf{n}} = ± \frac{1}{a}⟨x, y, 0⟩$, dS = adzdθ.

• Let’s say that we have the graph of a function z = f(x, y) and this is how we describe the surface (Figure 4).

$\hat{\mathbf{n}}dS = ±⟨-f_x, -f_y, 1⟩dxdy$ (🚀)

The last equation is a bit trick (Figure 0, 01, 02). $\vec{u}≈⟨ Δx, 0, f_xΔx⟩ = Δx⟨1, 0, f_x⟩, \vec{v}≈⟨0, Δy, f_yΔy⟩ = Δy⟨0, 1, f_y⟩$

Recall that the magnitude of the cross product of two vectors is the area of the parallelogram they enclose, and its direction is perpendicular to the plane containing those vectors, $\vec{u}x\vec{v} = ±\hat{\mathbf{n}}dS.$

$±\hat{\mathbf{n}}dS = \vec{u}x\vec{v} = (\begin{smallmatrix}\vec{i} & \vec{j} & \vec{k}\\ 1 & 0 & f_x\\ 0 & 1 & f_y\end{smallmatrix})ΔxΔy = ⟨-f_x, -f_y, 1⟩ΔxΔy$, and in the infinitesimal we got the previous formula (🚀). Notice that is ± because it is up to us to decide the direction of the normal vector (up or down).

• Exercise. $\vec{F} = z\vec{k}$ through the portion of paraboloid z = f(x, y) = x²+y² about the unit disk (Figure 03).

$\int \int_{S} \vec{F}·\hat{\mathbf{n}}·dS$ =[$\hat{\mathbf{n}}dS = ±⟨-f_x, -f_y, 1⟩dxdy$] $\int \int_{S}⟨0, 0, z⟩·⟨-2x, -2y, 1⟩dxdy = \int \int_{S} zdxdy = \int \int_{S} (x^2+y^2)dxdy$ =[Polar coordinates, the integral is really in the shadow region below the surface as it only involves x and y. We are also going to use a change from Cartesian to polar coordinates x = r·cos(θ), y = r·sin(θ), x²+y² = r², dA = rdrdθ] $\int_{0}^{2π} \int_{0}^{1} r^2·rdrdθ = \int_{0}^{2π}\frac{r^4}{4}\bigg|_{0}^{1} = $

$ = \int_{0}^{2π} \frac{1}{4}dθ = \frac{1}{4}θ\bigg|_{0}^{2π} = \frac{π}{2}.$

• Given a parametric description of a surface S, x = x(u, v), y = y(u, v), and z = z(u, v) or, alternatively, the position vector $\vec{r} = ⟨x, y, z⟩ = \vec{r}(u, v)$, let’s focus our attention in a small section of our section dS, then its sides will be defined (in terms of u, v) Δu, Δv, and we know that $\frac{∂\vec{r}}{∂u}Δu = ⟨\frac{∂\vec{x}}{∂u}Δu, \frac{∂\vec{y}}{∂u}Δu, \frac{∂\vec{z}}{∂u}Δu⟩$ and $\frac{∂\vec{r}}{∂v}Δv = ⟨\frac{∂\vec{x}}{∂v}Δv, \frac{∂\vec{y}}{∂v}Δv, \frac{∂\vec{z}}{∂v}Δv⟩$

$\frac{\partial \vec{r}}{\partial u}$ represents the partial derivative of the position vector $\vec{r}$ with respect to the parameter $u$. It describes how the position vector changes as the parameter $u$ changes, while keeping $v$ constant. $\Delta u$ corresponds to the change in the parameter that describes the surface S, their product is a vector that describes the change in position along the surface S in the direction of “u”. This vector is decomposed into its x, y, and z components, which represent the changes in the coordinates of a point on the surface as “u” changes.

$±\hat{\mathbf{n}}dS = $[By a similar argument as before, the cross product of the two vectors is the area of the parallelogram they enclose, and its direction is perpendicular to the plane containing those vectors] = $(\frac{∂\vec{r}}{∂u}Δu)x(\frac{∂\vec{r}}{∂v}Δv) =(\frac{∂\vec{r}}{∂u})x(\frac{∂\vec{r}}{∂v})ΔuΔv$

• If we know a normal vector $\vec{N}$ to the surface (not necessarily a unit vector), e.g., a plane give by the equation ax + by + cz = d, has a normal vector $\vec{N}$ = ⟨a, b, c⟩; a surface S given by an equation g(x, y, z) = 0, $\vec{N} = ∇g$. We want to relate ΔS to the area in the xy-plane (a projection in the xy-plane), ΔA = ΔS·cos(α) (Figure A).

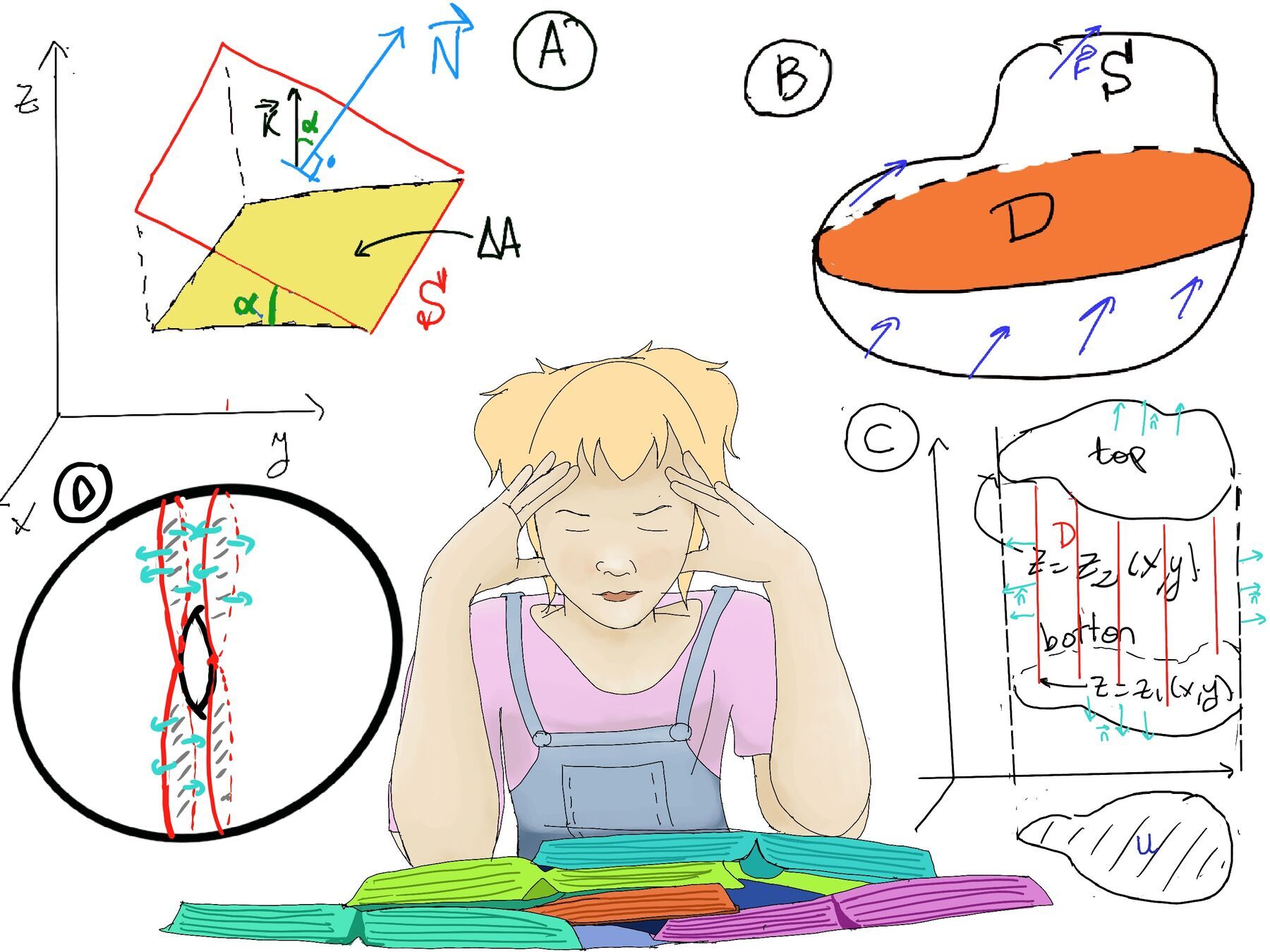
Notice that the angle α is also the angle between the two vectors perpendiculars to S and the plane xy, that is, $\vec{N}$ and $\vec{k}$ respectively ⇒ cos(α) = $\frac{\vec{N}\vec{k}}{|\vec{N}||\vec{k}}|=\frac{\vec{N}\vec{k}}{|\vec{N}|}$, hence ΔS = $\frac{|\vec{N}|}{\vec{N}\vec{k}}ΔA$ and what we are looking for, $\hat{\mathbf{n}}\frac{|\vec{N}|}{\vec{N}\vec{k}}ΔA$ [Recall that $\hat{\mathbf{n}}$ is a unit vector perpendicular to the surface] ±$\frac{\vec{N}}{\vec{N}\vec{k}}ΔA$. Finally, $\hat{\mathbf{n}}dS = ±\frac{\vec{N}}{\vec{N}\vec{k}}dxdy.$

Let’s see it in a example S where z -f(x, y) = 0 (Another way of putting it is g(x, y, z) = z -f(x, y)), $\vec{N} = ∇g = ⟨-f_x, -f_y, 1⟩$ ⇒ $\hat{\mathbf{n}}dS = \frac{\vec{N}}{\vec{N}\vec{k}}dxdy = \frac{⟨-f_x, -f_y, 1⟩}{⟨-f_x, -f_y, 1⟩\vec{k}}dxdy = \frac{⟨-f_x, -f_y, 1⟩}{1}dxdy = ⟨-f_x, -f_y, 1⟩dxdy.$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus and Calculus 3e (Apex). Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.