Triple Integrals

Without pain, without sacrifice, we would have nothing, Fight Club

Triple Integrals

Triple integrals are used in calculus to find the volume of a region in three-dimensional space bounded by surfaces. In other words, the triple integral of a function f(x, y, z) over a region R in three-dimensional space is expressed as or denoted by $\int \int \int f(x, y, z)dV$ where

1. f(x, y, z) is a function of three variables over a three-dimensional region.
2. dV represents an infinitesimal volume, dV = dx·dy·dz.
3. The integral is calculated over the region R and represents the volume of a solid region in three dimensonal spaces (Figure 1).

• Calculate the region between the paraboloids z = x² + y², z = 4 -x² -y², then the volume equals $\int \int \int 1dV$ (Figure 2 and 3)

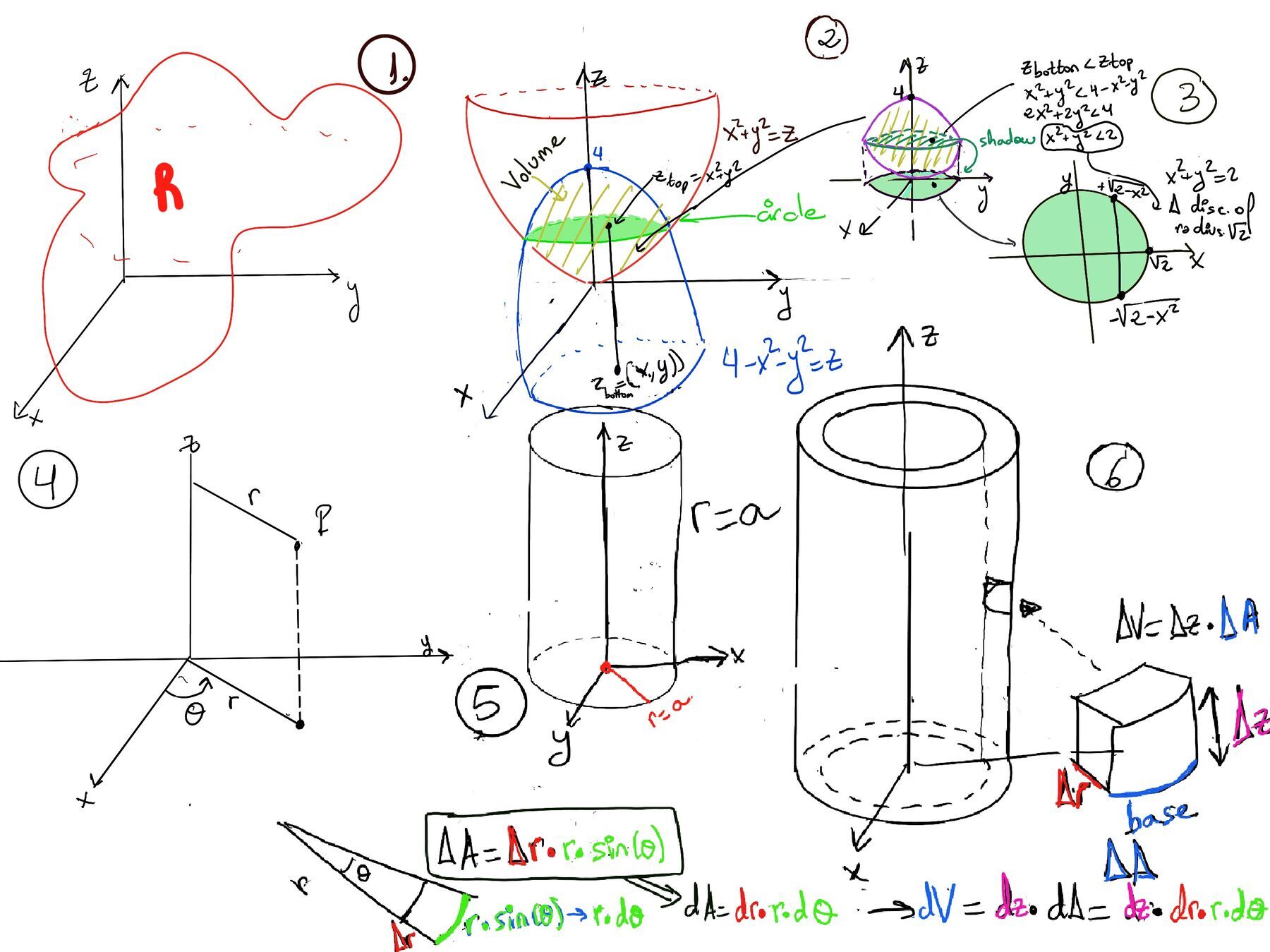
We first need to determine the limits of integration for the triple integral in Cartesian coordinates where the volume element dV is given by dx·dy·dz, are determined by the intersection of the two surfaces.

$\int \int \int 1dV = \int_{-\sqrt{2}}^{\sqrt{2}} \int_{-\sqrt{2-x^2}}^{+\sqrt{2-x^2}} \int_{x^2+y^2}^{4-x^2-y^2} dz·dy·dx$

$\int_{4-x^2-y^2}^{x^2+y^2} dz = z\bigg|_{4-x^2-y^2}^{x^2+y^2} = 4-2x^2-2y^2$

$\int \int \int 1dV = \int \int 4-2x^2-2y^2$

Evaluating triple integrals can be complex, so some techniques are used to simplify calculations.

In cylindrical coordinates, a Point (x, y, z) in a three-dimensional space is described using three coordinates (r, θ, z) (Figure 4 and 5 where r = a is a cylindrical surface that lies at a fixed radial distance a from the z-axis), where

1. r is the radial distance from the z-axis to the Point. It ranges between 0 to the radius of the intersection circle x²+y² = 2, that is, $\sqrt{2}.$
2. θ is the angle measured counterclockwise from the positive x-axis to the projection of P onto the xy plane. It ranges from 0 to 2π since we want to cover the entire circle, x²+y² = 2.
3. z is the height of P above (or below) the xy plane. It ranges from ${x^2+y^2} ~\text{to}~{4-x^2-y^2} ↭ r^2 ~\text{to}~ 4-r^2$

Recall z = z, x = rcos(θ), y = rsin(θ) ⇒ Combining these contributions together, we get the volume element dV in cylindrical coordinates: dV = rdrdθdz (see Figure 6).

$\int \int \int 1dV = \int_{0}^{2π} \int_{0}^{\sqrt{2}} \int_{r^2}^{4-r^2} dz·r·dr·dθ = $

$\int_{r^2}^{4-r^2} dz·r = r(4-r^2-r^2)=r(4-2r^2)$

$\int_{0}^{\sqrt{2}} r(4-2r^2)dr = \int_{0}^{\sqrt{2}}4rdr -\int_{0}^{\sqrt{2}}2r^3dr = 2r^2-\frac{1}{4}·2·r^4 = 2r^2-\frac{1}{2}r^4\bigg|_{0}^{\sqrt{2}} = 2·2-\frac{1}{2}·2^2 = 4-2 =2$

$\int \int \int 1dV = \int_{0}^{2π} 2dθ = 2θ\bigg|_{0}^{2π}=4π$

Hence, the volume of the region between the two paraboloids is just 4π.

Applications

Triple integrals have numerous applications in physics, engineering, and other fields and are used to calculate properties such as mass, moments of inertia, electric charge, etc. or volumes of three-dimensional objects.

Density offers a convenient means of obtaining the mass of a body from its volume or vice versa, $δ = \frac{m}{V}⇒dm = δ·dV.$ If we want to calculate the mass of a three-dimensional solid object, you will calculate the triple integral $\int \int \int_{R} δ·dV$. Of course, if δ = 1, the mass is just the volume.

The average value of a function of three variables f(x, y, z) in a region R, say occupied by a three-dimensional solid, is calculated $\overline {f} = \frac{1}{Vol(R)}·\int \int \int_{R} f·dV$. Besides, if this solid has a density, then the calculation varies a little, $\frac{1}{Mass(R)}·\int \int \int_{R} f·δ·dV$

The center of mass of a body or three-dimensional solid is the point where the entire mass of the body can be considered to be concentrated. It is an average of the masses factored by their distances from a reference point. It is denoted by $(\overline {x}, \overline {y}, \overline {z})$ and is calculated using the following formulas $\overline {x} = \frac{1}{Mass(R)}·\int \int \int_{R} x·δ·dV, \overline {y} = \frac{1}{Mass(R)}·\int \int \int_{R} y·δ·dV, \overline {z} = \frac{1}{Mass(R)}·\int \int \int_{R} z·δ·dV$. It will allow us to describe the position of the object as a whole, where the body would balance if it were placed on a perfectly frictionless support, e.g., the point where you would put your finger to balance your ruler. For a uniform body, the center of mass coincides with its geometric center.

Moment of Inertia is the tendency of a body to maintain its state of rotation or rest. If the body is in rest, it tries to remain at rest and resist any force trying to bring it into motion. If the body is in rotational motion, it is the tendency which opposes the change in its rotational motion due to external forces, the body tries to continue in motion and resist any force trying to bring it to change its motion.

The moment of inertia of a body about a given axis is a measure of the body’s resistance to rotational motion about that axis. The general formula is I = mr² where m is the mass of the object and r the distance from the axis of rotation. It is calculated using the formula $\int \int \int_{R} (distanceToAxis)^2·δ·dV$. Higher moment of inertia implies that it is harder to change the body’s rotational motion about that axis.

The moment of inertia of a body about the z-axis, $I_z = \int \int \int_{R} r^2·δ·dV$ =[Cartesian coordinates] $\int \int \int_{R} (x^2+y^2)·δ·dV$. By symmetry, $I_y = \int \int \int_{R} (x^2+z^2)·δ·dV, I_x = \int \int \int_{R} (u^2+z^2)·δ·dV$

• I_z of a solid cone between z = ar and z = b with no density (δ = 1) (Figure A).

$I_z = \int \int \int_{R} r^2·δ·dV = \int \int \int_{R} r^2·dV = \int \int \int_{R} r^2·rdrdθdz = \int_{0}^{b} \int_{0}^{2π} \int_{0}^{\frac{z}{a}} r^3drdθdz$

$\int_{0}^{\frac{z}{a}} r^3dr = \frac{r^4}{4}\bigg|_{0}^{\frac{z}{a}} = \frac{(\frac{z}{a})^4}{4}$

$\int_{0}^{2π} \frac{(\frac{z}{a})^4}{4} dθ = \frac{(\frac{z}{a})^4}{4}θ\bigg|_{0}^{2π} $

$= \frac{(\frac{z}{a})^4}{4}θ \bigg|_{0}^{2π} = \frac{z^4}{a^4}2π\frac{1}{4} = \frac{z^4π}{2a^4}$

$I_z = \int_{0}^{b} \frac{z^4π}{2a^4}dz = \frac{z^5π}{5·2·a^4}\bigg|_{0}^{b} = \frac{πb^5}{10a^4}$

• Calculate the volume for the region z > 1 -y inside the unite ball (x²+ y²+z² = 1, Figure B).

$I_z = \int_{0}^{1} \int_{-\sqrt{2y -2y^2}}^{\sqrt{2y -2y^2}} \int_{1-y}^{\sqrt{1-x^2-y^2}} dzdxdy$, this is not an easy integral, so it will be wise to use symmetry and it is left to the reader to do so.

Notice that y fixed ⇒ z ranges between touching the sphere $\sqrt{1-x^2-y^2}$ and the plane z = 1-y. Similarly, x are elements that ranges inside $1-y < \sqrt{1-x^2-y^2}⇒ (1-y)^2 < 1-x^2-y^2 ⇒ 1 +y^2 -2y < 1-x^2-y^2 ⇒x^2 < 2y -2y^2$,

so x ranges between $\sqrt{2y -2y^2}$ and $-\sqrt{2y -2y^2}$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, Andrew Misseldine, and MathMajor, YouTube’s channels.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. MIT OpenCourseWare, 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007, YouTube.
8. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.