Spherical coordinates

Life is a math equation. In order to gain the most, you have to know how to convert negatives into positives, Anonymous.

Pure mathematics is, in its way, the poetry of logical ideas, Albert Einstein.

Spherical coordinates

Spherical coordinates are a system for representing points in three-dimensional space (P) using three parameters: radial distance r, polar angle θ, and azimuthal angle ϕ. In other words, it describes or specifies the position of a point in three-dimensional space by three numbers (r, θ, φ) (Figure i)

• r (ρ) is the radial distance from the origin to the point. It values range from 0 to infinity.
• φ is the polar angle, measured between the z-axis and the radial line r. It values increases from 0 (positive z-axis), π/2 (xy-plane), and π (negative z-axis), that is, 0 ≤ θ ≤ π.
• θ is the azimuthal angle, measured between the projection of the radial line on the xy-plane and the positive x-axis.

They make it simple to describe a sphere (ρ = a are spheres of radius a centered at the origin), just as cylindrical coordinates make it easy to describe a cylinder (Figure ii).

Let’s consider the plane of the visual field as being a representation of the xy plane, Figure 3, and we get z = ρcos(φ), r = ρsin(φ) ⇒[Cylindrical conversion formulas, x = rcos(θ), y = rsin(θ), z = z] x = rcos(θ) = ρsin(θ)cos(θ), y = rsin(θ) = ρsin(θ)sin(θ), and z = ρcos(φ).

φ = ^π⁄₄ is a cone (Figure iv), φ = ^π⁄₂ is the xy plane.

We are trying to calculate triple integral, so we need to know dV (Figure v), and we obtain dV = ρ²sin(φ)dρdφdθ.

• Calculate the volume of the unit sphere above z = $\frac{1}{\sqrt{2}}$ (Figure A)

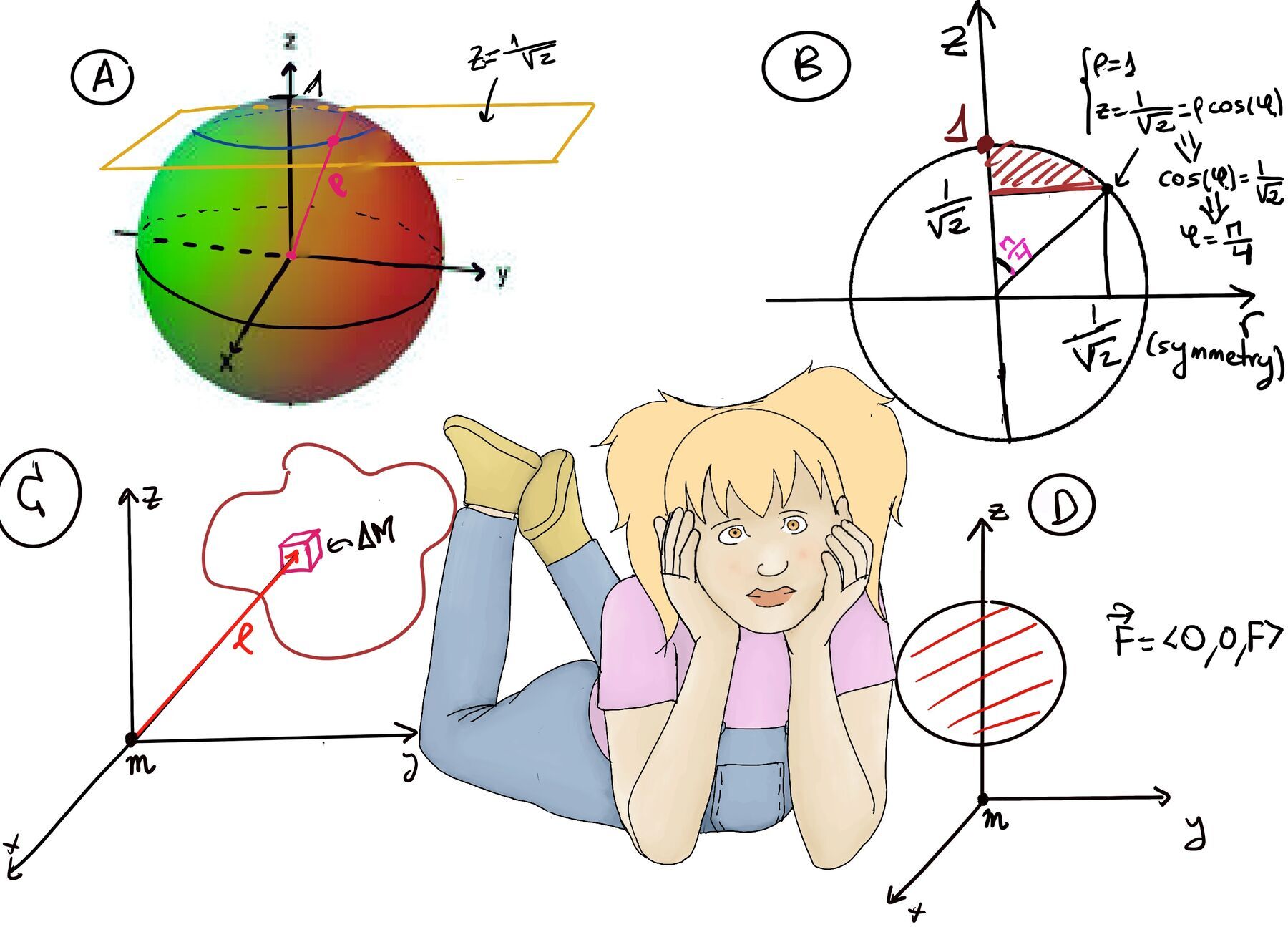
V = $\int \int \int 1·dV = \int \int \int 1·ρ^2sin(φ)dρdφdθ = $[We leave the sphere when ρ = 1 and enter the region where we enter the plane ↭ $z = \frac{1}{\sqrt{2}}⇒ ρcos(φ) = \frac{1}{\sqrt{2}} ⇒ ρ = \frac{1}{cos(φ)\sqrt{2}} = \frac{sec(φ)}{\sqrt{2}} $ ]$ = \int \int \int_{\frac{sec(φ)}{\sqrt{2}}}^{1} ρ^2sin(φ)dρdφdθ$ = The lower bound for φ is easy as we start at the North Pole when φ = 0, Figure B illustrates the other bound. $\int \int_{0}^{\frac{π}{4}} \int_{\frac{sec(φ)}{\sqrt{2}}}^{1} ρ^2sin(φ)dρdφdθ$ = [As we move all move all around the z axis, θ ∈ [0, 2π]] $\int_{0}^{2π} \int_{0}^{\frac{π}{4}} \int_{\frac{sec(φ)}{\sqrt{2}}}^{1} ρ^2sin(φ)dρdφdθ = \frac{2π}{3}-\frac{5π}{6\sqrt{2}}$

$ \int_{0}^{2\pi} \int_{0}^{\frac{\pi}{4}} \int_{\frac{\sec(\phi)}{\sqrt{2}}}^{1} \rho^2 \sin(\phi) , d\rho , d\phi , d\theta = \int_{0}^{2\pi} \int_{0}^{\frac{\pi}{4}} \left[ \frac{1}{3} \rho^3 \sin(\phi) \right]_{\frac{\sec(\phi)}{\sqrt{2}}}^{1} d\phi d\theta \quad =$

$\int_{0}^{2\pi} \int_{0}^{\frac{\pi}{4}} \left( \frac{1}{3} \sin(\phi) - \frac{1}{3·2·\sqrt{2}} \sec^3(\phi) \sin(\phi) \right) \ d\phi \ d\theta$

$\int_{0}^{2\pi} \left[ -\frac{1}{6\sqrt{2}} \int_{0}^{\frac{\pi}{4}} \sec^3(\phi) \sin(\phi) d\phi + \frac{1}{3} \int_{0}^{\frac{\pi}{4}} \sin(\phi) d\phi \right] d\theta \quad$

$\frac{1}{3} \int_{0}^{\frac{\pi}{4}} \sin(\phi) d\phi = -cos(\phi)\bigg|_{0}^{\frac{\pi}{4}} = -cos(\frac{\pi}{4})+cos(0)=-\frac{\sqrt{2}}{2}+1$

$\int_{0}^{\frac{\pi}{4}} \sec^3(\phi) \sin(\phi) d\phi$ =[… Left to the Reader, but it will be long and painful like a kick to the groin+]a

Calculation of Gravitational Force Exerted by an object

The gravitational force is a force that attracts any two objects with mass. Newton’s law of universal gravitation states that every particle in the universe attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers.

The equation for universal gravitation thus takes the form, $F = G\frac{m_1m_2}{r^2}$ where F is the gravitational force acting between the two objects (masses), m₁ and m₂ are the masses of the two objects, r is the distance between the centers of their masses, and G is the gravitational constant.

We want to calculate the gravitational force $\vec{F}$ exerted by an object on a mass m located at the origin. To calculate the gravitational force exerted by a small differential mass ΔM located at coordinates (x, y, z) on a mass m located at the origin we use the formula:

$|\vec{F}| = G\frac{ΔM·m}{ρ^2}, dir(\vec{F}) = \frac{⟨x, y, z⟩}{ρ}$ where $|\vec{F}|$ is the magnitude of the gravitational force, ρ is the distance from the differential mass to the origin, ⟨x, y, z⟩ is the position vector of the differential mass, and the direction of the force is a unit vector. Therefore, $\vec{F} = \frac{G·ΔM·m}{ρ^3}⟨x, y, z⟩$ (Figure C).

To calculate the gravitational force exerted by the entire object, we integrate the gravitational force over the entire volume occupied by the object.

Recall that ΔM = δ· ΔV, where δ is the density, and ΔV is the volume element.

$\vec{F} = \int \int \int \frac{G·m·⟨x, y, z⟩}{ρ^3}δdV$ =[It is complex enough, so it is very useful to simplify by using spherical coordinates and place the solid in a way that the z-axis is an axis of symmetry, so the gravitational force will be directed along the z-axis -Figure D-, that is, $\vec{F}=⟨0, 0, z⟩$] =$\int \int \int \frac{G·m·z}{ρ^3}δdV = \int \int \int \frac{G·m·ρcos(φ)}{ρ^3}δ·ρ^2sin(φ)dρdφdθ = Gm \int \int \int δ·cos(φ)sin(φ)dρdφdθ$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus and Calculus 3e (Apex). Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.