T de Student, correlaciones y regresión lineal

Pruebas T para una y dos muestras independientes

Las pruebas T de dos muestras independientes se emplean cuando se obtienen dos grupos de muestras aleatorias, independientes (no relacionados o no emparejados) e idénticamente distribuidas. Se utilizan para comparar las medias de los dos grupos.

Por ejemplo, usemos rnorm para generar dos vectores de números aleatorios distribuidos normalmente (x = rnorm (100), y = rnorm (100), si no se especifican argumentos, media = 0, sd = 1). t.test (x, y) realiza una prueba t de dos muestras independientes comparando las medias de los dos grupos (x, y, H₀: mx = my or mx - my = 0 ). Por defecto, alternative=“two.sided” H_a: mx - my ≠ 0. p-value = 0.2162 no es inferior o igual al nivel crítico o de significancia 0.05, por lo que no podemos rechazar la hipótesis nula.

Sin embargo, x₂=rnorm(100, 2), generamos otro vector de números aleatorios pero, en esta ocasión, distribuidos normalmente con media = 2 y sd = 1. t.test(x, x₂) realiza una prueba t de dos muestras independientes comparando las medias de x y x₂. El valor p <2.2e-16 es inferior al nivel de significación 0.05, por lo que podemos rechazar la hipótesis nula. Dicho de otro modo, podemos concluir que las medias de x e x₂ son significativamente diferentes.

Sin embargo, vayamos más despacio y seamos un poco más rigurosos. En primer lugar, definimos los vectores:

x=rnorm(100)
y=rnorm(100)

Debemos considerar que la prueba t de dos muestras independientes requiere que los dos grupos de observaciones estén distribuidos normalmente (shapiro_test(x) devuelve p.value = 0.8622367 > 0.05 y shapiro_test(y) devuelve p.value = 0.1753192> 0.05), por lo que la distribución de los datos no es significativamente diferente a una distribución normal. Por tanto, podemos asumir la normalidad. Además, ambas varianzas deben ser iguales.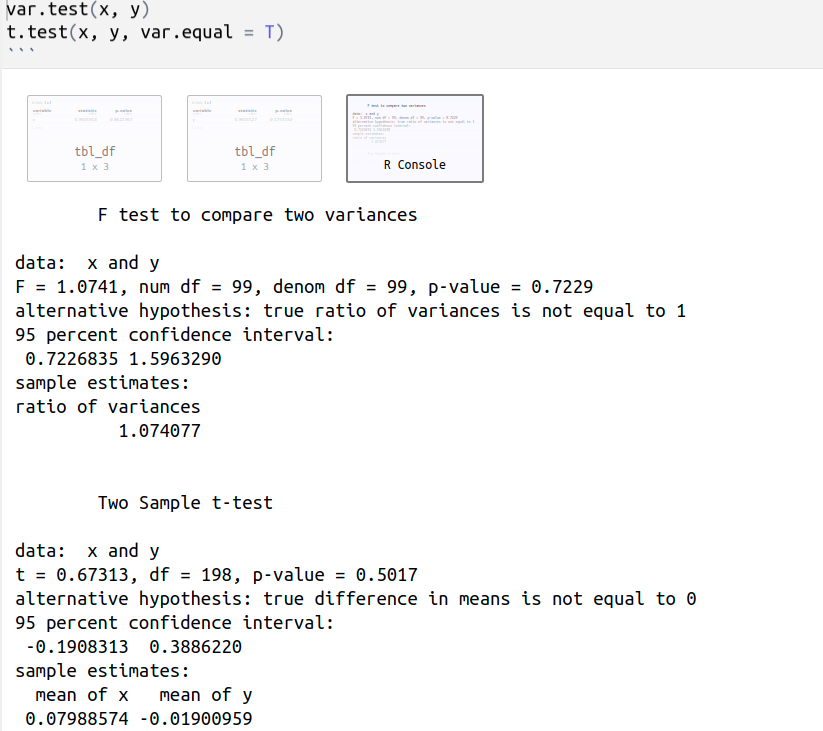

var.test(x, y) realiza una prueba F para comparar las varianzas de las dos muestras. El valor p de la prueba F = 0,7229> 0,05, por lo que no hay una diferencia significativa entre las varianzas de ambas muestras, podemos asumir la igualdad de las dos varianzas.

t.test(x, y, var.equal = T) realiza una prueba t de dos muestras asumiendo varianzas iguales, p-value = 0.5017 > 0.05, por lo que no podemos rechazar la hipótesis nula, H₀: mx = my or mx - my = 0.

x=rnorm(100)
y=rnorm(100, mean=2)
var.test(x, y)
t.test(x, y, var.equal = T)

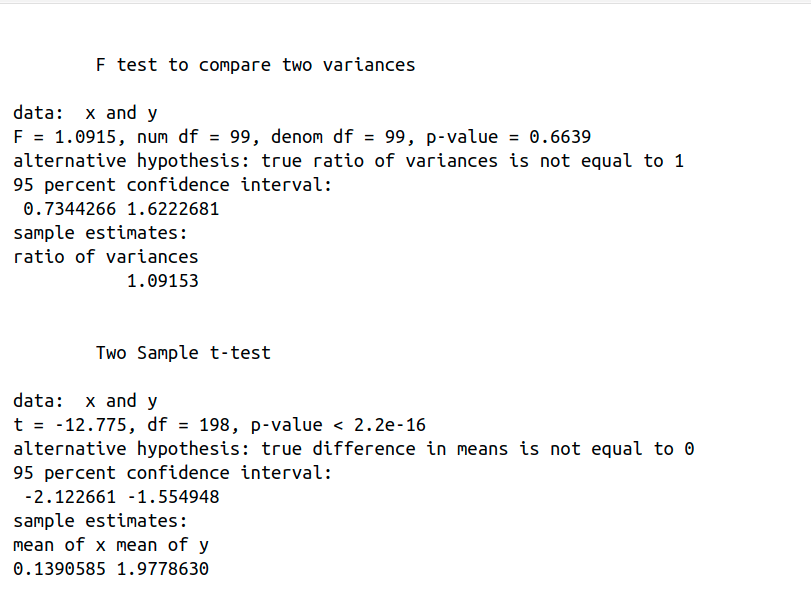
var.test(x, y) realiza una prueba F para comparar las varianzas de las dos muestras. El valor p de la prueba F = 0,6639> 0,05, por lo que no hay una diferencia significativa entre las varianzas de ambas muestras y podemos asumir igualdad de varianzas.

Tal como previamente comentamos, t.test (x, y, var.equal = T) realiza una prueba t de dos muestras independientes. Obtenemos que p-value < 2.2e-16, por lo que podemos rechazar la hipótesis nula y concluir que las medias de los grupos x e y son significativamente diferentes.

Tomemos datos del libro Probability and Statistics with R: install.packages(“PASWR”) (install.packages instala un paquete determinado), library(“PASWR”) (library carga un paquete determinado, es decir, lo añade y lo pone disponible a la lista de búsqueda en tu espacio de trabajo en R). Fertilize muestra un data frame o marco de datos de las alturas de las plantas, en pulgadas, de dos grupos de semillas, una obtenida por fertilización cruzada y la otra por auto fertilización.

   cross   self
1  23.500 17.375
2  12.000 20.375
3  21.000 20.000
4  22.000 20.000
5  19.125 18.375
6  21.500 18.625
7  22.125 18.625
8  20.375 15.250
9  18.250 16.500
10 21.625 18.000
11 23.250 16.250
12 21.000 18.000
13 22.125 12.750
14 23.000 15.500
15 12.000 18.000

> names(Fertilize) # names es una función que devuelve los nombres de las variables del data frame o marco de datos 
Fertilize [1] "cross" "self"

> summary(self) # summary es otra función que calcula resúmenes estadísticos de self: Min (el valor mínimo), 1st Qu. (el primer cuartil), Median (el valor de la mediana), Mean (Media), 3er Qu. (el tercer cuartil) y Max (el valor máximo)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  12.75   16.38   18.00   17.57   18.62   20.38

library(ggpubr) 
ggboxplot(self, xlab = "Self", ylab = "Heights", # Visualicemos nuestros datos 
ggtheme = theme_light()) # Lo usamos para modificar o personalizar el tema o la apariencia del gráfico 

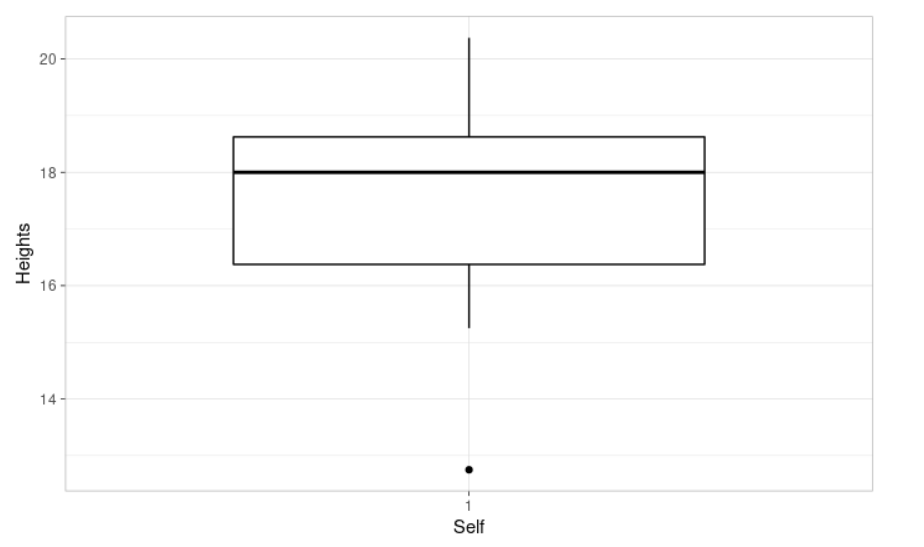
Se utiliza una prueba t de una muestra para comparar la media de una muestra con un valor conocido o predeterminado (μ). Podemos definir la hipótesis nula como H₀: m = μ. La hipótesis alternativa correspondiente es H_a: m ≠ μ. Supone que los datos tienen una distribución normal. Vamos a comprobarlo.

> shapiro.test(self)

	Shapiro-Wilk normality test

data:  self
W = 0.93958, p-value = 0.3771

Utilizamos la prueba de normalidad de Shapiro-Wilk. La hipótesis nula es la siguiente, H₀: los datos se distribuyen normalmente. La hipótesis alternativa correspondiente es H_a: los datos no se distribuyen normalmente.

Observando los resultados obtenidos, el valor p = 0.3771> 0.05 implica que no podemos rechazar la hipótesis nula (la distribución de los datos no es significativamente diferente a la de una distribución normal) y, en consecuencia, podemos suponer que los datos tienen una distribución normal.

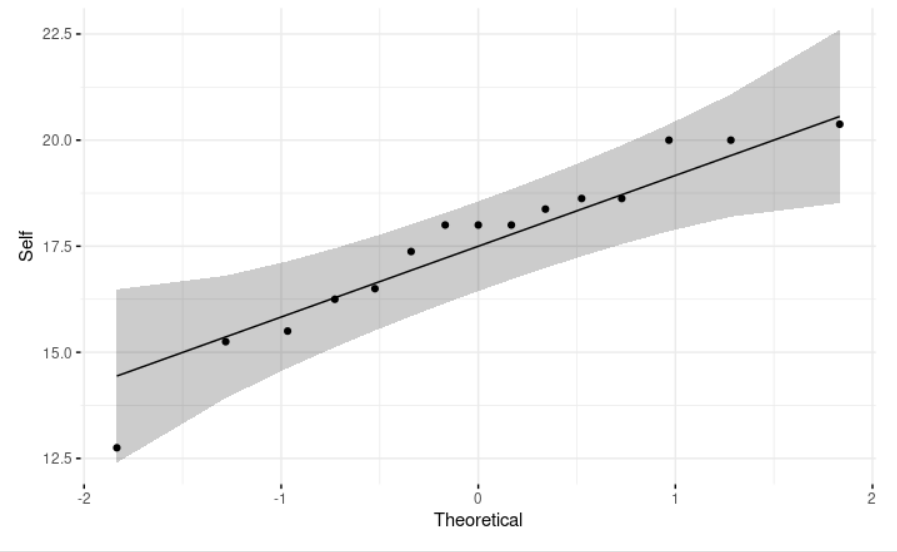
ggqqplot(self, ylab = "Self", # Usamos una gráfica Q-Q (cuantiles-cuantiles) que compara los percentiles empíricos de un conjunto de datos con los percentiles teóricos de una distribución normal. Nos permite evaluar visualmente el supuesto de normalidad y observamos que, como esperábamos, **los puntos se distribuyen aproximadamente en una línea recta**. 
ggtheme = theme_minimal())

Queremos saber si la altura promedio, en pulgadas, de las plantas obtenidas por autofecundación es 17.

> t.test(self, mu=17, conf=.95)

	One Sample t-test

data:  self
t = 1.0854, df = 14, p-value = 0.2961
alternative hypothesis: true mean is not equal to 17
95 percent confidence interval:
 16.43882 18.71118
sample estimates:
mean of x 
   17.575

El valor del estadístico t es 1.0854, su p-value es 0.2961, que es mayor que el nivel de significación 0.05. No tenemos ninguna razón para rechazar la hipótesis nula, H₀: m = 17. También nos da un intervalo de confianza para la media: [16.43882, 18.71118]. Observa que la media hipotética µ = 17 cae dentro del intervalo de confianza.

A continuación, queremos saber si la media de las alturas de las plantas obtenidas por fertilización cruzada es significativamente diferente de la obtenida por autofecundación.

> summary(cross) # summary devuelve resúmenes estadísticos de cross: Min (el valor mínimo), 1st Qu. (el primer cuartil), Median (el valor de la mediana), Mean (Media), 3er Qu. (el tercer cuartil) y Max (el valor máximo)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  12.00   19.75   21.50   20.19   22.12   23.50  
> library(ggpubr)
> boxplot(cross, self, ylab = "Height", xlab = "Method") # Visualicemos nuestros datos

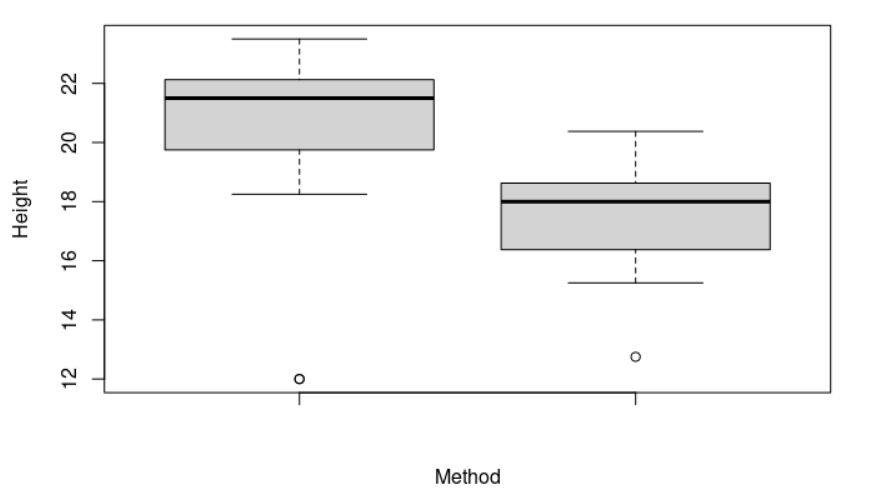
En nuestro gráfico podemos observar que ambas muestras tienen medias muy diferentes. ¿Tienen las dos muestras diferentes varianzas?

> var.test(cross, self)

	F test to compare two variances

data:  cross and self
F = 3.1079, num df = 14, denom df = 14, p-value = 0.04208
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 1.043412 9.257135
sample estimates:
ratio of variances 
          3.107894

var.test(cross, self) realiza una prueba F para comparar las varianzas de las dos muestras. El valor p de la prueba F = 0.04208 <0.05 y, en consecuencia, hay una diferencia significativa entre las varianzas de ambas muestras, no podemos asumir la igualdad de varianzas.

Anteriormente explicamos que uno de los requerimientos para la prueba t es que las varianzas de las dos muestras deben ser iguales. Sin embargo, se utiliza una modificación de la prueba t, conocida como prueba de Welch, para resolver este problema. En realidad, es la opción predeterminada en R, pero siempre se puede especificar con el argumento var.equal = FALSE.

> t.test(cross, self, conf=.95)

	Welch Two Sample t-test

data:  cross and self
t = 2.4371, df = 22.164, p-value = 0.02328
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 0.3909566 4.8423767
sample estimates:
mean of x mean of y 
 20.19167  17.57500

El valor de la prueba t de dos muestras de Welch es 2.4371, su p-value es 0.02328 < 0.05, que es menor que el nivel de significancia 0.05. Entonces rechazamos la hipótesis nula y, por consiguiente, podemos concluir que existe una diferencia significativa entre ambas medias.

> shapiro.test(cross) # Sin embargo, no hemos comprobado que los datos de la muestra "fertilización cruzada" sigan una distribución normal

	Shapiro-Wilk normality test

data:  cross
W = 0.753, p-value = 0.0009744 # De la salida que nos devuelve R, p-value = 0.0009744 < 0.05 lo que implica que la distribución de los datos es significativamente diferente a una distribución normal. Dicho de otro modo, no podemos asumir la normalidad.

> wilcox.test(self, cross, exact=FALSE) # Si los datos no están distribuidos normalmente, se recomienda utilizar la prueba no paramétrica de Wilcoxon.

	Wilcoxon rank sum test with continuity correction

data:  self and cross
W = 39.5, p-value = 0.002608
alternative hypothesis: true location shift is not equal to 0

El p-value de la prueba es 0.002608, que es menor que el nivel de significancia 0.05. Podemos concluir que la media de las alturas de las plantas obtenidas por fertilización cruzada es significativamente diferente de la media de las plantas obtenidas por autofecundación.

Impacto de la violencia en los medios de comunicación

Sigamos adelante con otro ejemplo. “Prácticamente desde los albores de la televisión, padres, maestros, legisladores y profesionales de la salud mental han querido comprender el impacto de los programas de televisión, particularmente en los niños,” Violencia en los medios: Los psicólogos estudian sus posibles efectos negativos, American Psychological Association. Más específicamente, queremos evaluar el impacto de ver programas violentos en los espectadores.

library("PASWR") # Carga el paquete PASWR
attach(Aggression)

Se trata de un data frame o marco de datos sobre el comportamiento agresivo en relación con la exposición a programas de televisión violentos. En cada una de las 16 parejas resultantes, un niño es seleccionado al azar para ver programas violentos (violence), mientras que al otro se le hace visualizar dibujos animados, comedias de situación y similares (noviolence)

Aggression # Muestra el marco de datos en formato tabular. 

> summary(violence) # summary produce resúmenes estadísticos de violence: Min (el valor mínimo), 1st Qu. (el primer cuartil), Median (el valor de la mediana), Mean (Media), 3er Qu. (el tercer cuartil) y Max (el valor máximo)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  14.00   16.75   23.00   25.12   35.00   40.00 
> summary(noviolence)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
   7.00   16.00   19.00   20.56   26.50   33.00 
> library(ggpubr)
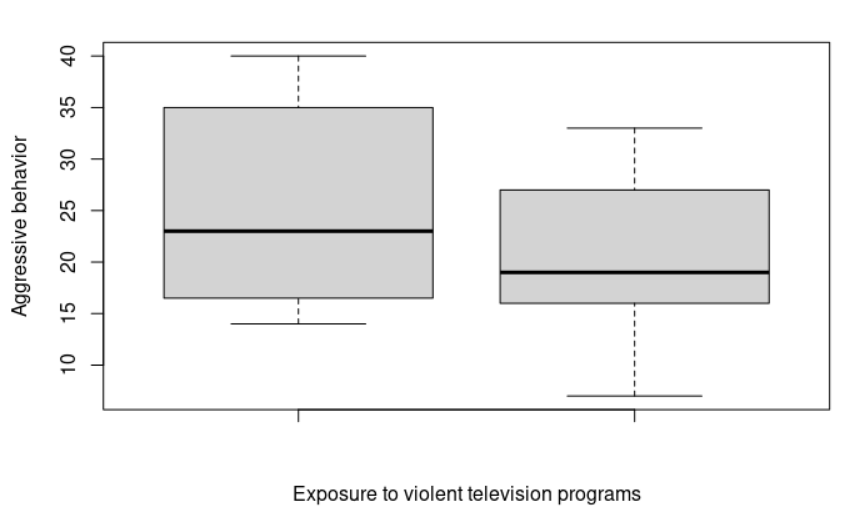
> boxplot(violence, noviolence, ylab="Aggressive behavior", xlab="Exposure to violent television programs") # Visualicemos nuestros datos

> shapiro.test(violence)

	Shapiro-Wilk normality test

data:  violence
W = 0.89439, p-value = 0.06538

> shapiro.test(noviolence)

	Shapiro-Wilk normality test

data:  noviolence
W = 0.94717, p-value = 0.4463

Observamos que los p-values (o p valores) son 0.06538 y 0.4463, es decir, ambos son mayores que el nivel de significación 0.05. Entonces, no podemos rechazar la hipótesis nula, la distribución de los datos no es significativamente diferente a una distribución normal en ambas condiciones (violencia y noviolencia) y podemos asumir que los datos siguen una distribución normal.

> var.test(violence, noviolence)

	F test to compare two variances

data:  violence and noviolence
F = 1.4376, num df = 15, denom df = 15, p-value = 0.4905
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.5022911 4.1145543
sample estimates:
ratio of variances 
          1.437604

var.test(violence, noviolence) realiza una prueba F para comparar las varianzas de las dos muestras. El valor p de la prueba F = 0.4905 > 0.05, es decir, no hay una diferencia significativa entre las varianzas de ambas muestras y podemos asumir la igualdad de las dos varianzas.

> t.test(violence, noviolence)

	Welch Two Sample t-test

data:  violence and noviolence
t = 1.5367, df = 29.063, p-value = 0.1352
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -1.509351 10.634351
sample estimates:
mean of x mean of y 
  25.1250   20.5625 

> t.test(violence, noviolence, var.equal = T)

	Two Sample t-test

data:  violence and noviolence
t = 1.5367, df = 30, p-value = 0.1349
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -1.501146 10.626146
sample estimates:
mean of x mean of y 
  25.1250   20.5625** 

t.test(violence, noviolence, var.equal = T) realiza una prueba t de dos muestras asumiendo varianzas iguales, valor p = 0.1349 > 0.05, por lo que no podemos rechazar la hipótesis nula. Podemos concluir que no existe una diferencia estadísticamente significativa con respecto al comportamiento violento en relación a la exposición a programas de televisión violentos. Quiero que observes que las estadísticas de Welch producen resultados similares.

Análisis de correlación en R

Las variables dentro de un conjunto de datos pueden estar relacionadas por muchas razones. Una variable puede ser la causa o depender de los valores de otra variable, puede ser causa y efecto al mismo tiempo o ambas pueden verse afectadas por una tercera variable. La relación estadística entre dos variables se conoce como su correlación y se utiliza una prueba de correlación para evaluar si existe alguna asociación entre dos o más variables.

Una correlación puede ser positiva, lo que significa que a valores altos de una variable corresponden valores altos de la otra y a valores bajos de una variable corresponden valores bajos de la otra, es decir, los valores de ambas variables cambian en el mismo sentido. Un ejemplo sería la altura y el peso, las personas más altas tienden a ser más pesadas. También, puede ser negativa, lo que significa que cuando los valores de una variable aumentan, los valores de la otra variable disminuyen y viceversa, es decir, los valores de ambas variables cambian en sentido contrario. Un ejemplo sería ejercicio físico y peso, las personas que practican más ejercicio físico y tienen una vida más activa, suelen tener menos peso. La correlación también puede ser cero, lo que significa que las variables no están relacionadas o son independientes entre sí. Por ejemplo, no existe una relación entre la cantidad de Coca-Cola que bebe una persona y su nivel de ingresos.

Un coeficiente de correlación determina la fuerza de la relación entre dos variables. Hay tres tipos de coeficientes de correlación: Pearson, Spearman y Kendall. La más utilizada es la correlación de Pearson. Es una medida de dependencia lineal entre dos variables aleatorias cuantitativas.

Usemos un conjunto de datos del Statistics Online Computational Resource, Recurso computacional en línea de estadísticas (SOCR). Contiene la altura (pulgadas) y el peso (libras) de 25.000 personas de 18 años de edad. El archivo SOCR-HeightWeight.csv contiene los siguientes datos:

Index,Height,Weight # La primera línea es índice, altura (pulgadas), peso (libras)
1,65.78331,112.9925
2,71.51521,136.4873
3,69.39874,153.0269
4,68.2166,142.3354
5,67.78781,144.2971
6,68.69784,123.3024
7,69.80204,141.4947
8,70.01472,136.4623
9,67.90265,112.3723 […]

weightHeight <- read.table("/path/SOCR-HeightWeight.csv", header = T, sep = “,”) # read.table carga nuestro archivo de datos en R, usamos sep = “,” para especificar el carácter separador y nos devuelve un data frame o marco de datos weightHeight

library("ggpubr")
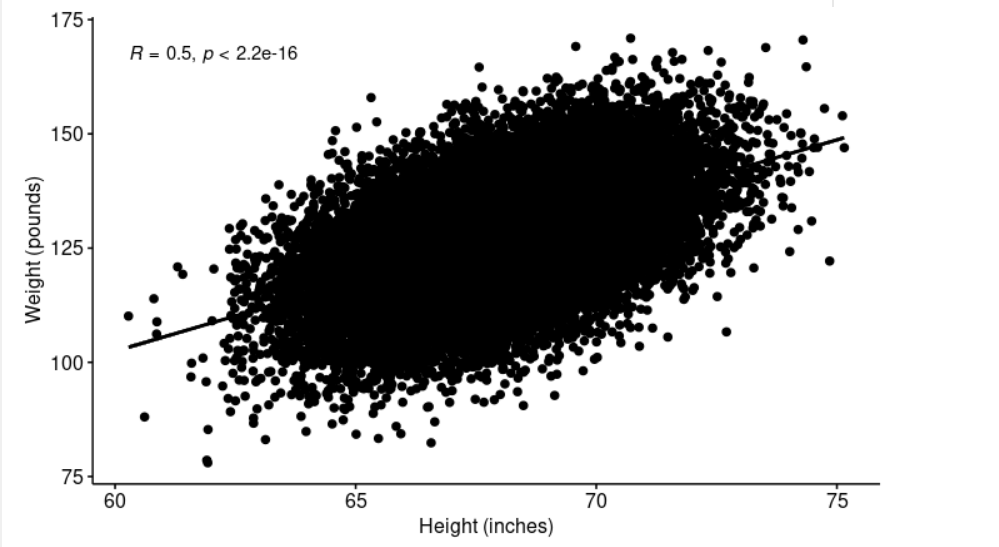
ggscatter(weightHeight, x = "Height", y = "Weight", # Visualicemos nuestros datos, x e y son las variables a representar
          add = "reg.line", conf.int = TRUE, # add = "reg.line" indica que añada la recta de regresión y conf.int = TRUE, el intervalo de confianza.
          cor.coef = TRUE, cor.method = "pearson", # cor.coef = TRUE especifica que incluya también el coeficiente de correlación y cor.method = "pearson" es el método que seleccionamos para calcular el coeficiente de correlación. 
          xlab = "Height (inches)", ylab = "Weight (pounds)")

> shapiro.test(weightHeight$Height[0:5000])

Podemos comprobar en el gráfico anterior, que la relación es lineal. ¿Mis datos (peso, altura) siguen una distribución normal? La prueba de Shapiro no puede operar con más de 5.000 observaciones. Vamos a realizar la prueba de shapiro pero usando solo las primeras 5.000.

	Shapiro-Wilk normality test

data:  weightHeight$Height[0:5000]
W = 0.99955, p-value = 0.2987
> shapiro.test(weightHeight$Weight[0:5000])

	Shapiro-Wilk normality test

data:  weightHeight$Weight[0:5000]
W = 0.99979, p-value = 0.9355

Observamos que los dos valores p (0.2987, 0.9355) son mayores que el nivel crítico de significación 0.05. Por lo tanto, no podemos rechazar la hipótesis nula, las distribuciones de los datos de cada una de las dos variables no son significativamente diferentes a las de la distribución normal. Dicho con otras palabras, podemos asumir normalidad.

Podemos usar gráficos Q-Q (cuantiles-cuantiles) que comparan los percentiles empíricos de un conjunto de datos con los percentiles teóricos de una distribución normal para comprobar visualmente el supuesto de normalidad: library(“ggpubr”), ggqqplot(weightHeight$Height, ylab = “Height”), ggqqplot(weightHeight$Weight, ylab = “Weight”).

> cor.test(weightHeight$Height, weightHeight$Weight)

	Pearson's product-moment correlation

data:  weightHeight$Height and weightHeight$Weight
t = 91.981, df = 24998, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.4935390 0.5120626
sample estimates:
      cor 
0.5028585

cor.test realiza una prueba de correlación entre dos variables. Devuelve tanto el coeficiente de correlación como el nivel de significación (o valor p) de la correlación. El valor estadístico de la prueba t es 91.981, su valor p es < 2.2e-16, por lo que podemos concluir que la altura y el peso están correlacionados significativamente de manera positiva (r = 0.5028585, p-value < 2.2e-16).

Regresión lineal en R

La regresión lineal es un modelo para estimar o analizar la relación entre una variable dependiente o respuesta (típicamente se denomina “y”) y una o más variables independientes o explicativas. Dicho de otro modo, la regresión lineal predice un valor para Y, ‘dado’ un valor de X.

Se supone que existe una relación lineal entre la variable de respuesta y las variables explicativas. Gráficamente, una relación lineal es una línea recta cuando se traza en un gráfico. Su ecuación general es y = b₀ + b₁*x + e donde y es la variable de respuesta, x es el predictor, variable independiente o explicativa, b₀ es la intersección de la línea de regresión y el eje de ordenadas (el valor predicho cuando x = 0), b₁ es la pendiente de la línea de regresión, y “e” es el término de error o el error residual, es decir, la parte de la variable de respuesta que el modelo de regresión no puede explicar.

Usemos nuestro conjunto de datos del Recurso computacional en línea de estadísticas, Statistics Online Computational Resource (SOCR). Contiene la altura (pulgadas) y el peso (libras) de 25.000 jóvenes de 18 años de edad. El archivo SOCR-HeightWeight.csv contiene los siguientes datos:

weightHeight <- read.table("/path/SOCR-HeightWeight.csv", header = T, sep = ",") 
# read.table carga nuestro archivo de datos en R, usamos sep = "," para especificar el carácter separador y nos devuelve un data frame o marco de datos
weightHeight

library("ggpubr")
ggscatter(weightHeight, x = "Height", y = "Weight", # Visualicemos nuestros datos, x e y son las variables a representar
          add = "reg.line", conf.int = TRUE, # add = "reg.line" indica que añada la recta de regresión y conf.int = TRUE, el intervalo de confianza.
          cor.coef = TRUE, cor.method = "pearson", # cor.coef = TRUE especifica que también incluya el coeficiente de correlación y cor.method = "pearson" es el método que seleccionamos para calcular dicho coeficiente de correlación.  
          xlab = "Height (inches)", ylab = "Weight (pounds)")

El gráfico anterior sugiere una clara relación lineal entre la altura y el peso.

> cor.test(weightHeight$Height, weightHeight$Weight)

	Pearson's product-moment correlation

data:  weightHeight$Height and weightHeight$Weight
t = 91.981, df = 24998, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.4935390 0.5120626
sample estimates:
      cor 
0.5028585

El coeficiente de correlación determina la fuerza de la relación entre dos variables. Un coeficiente de correlación de r = .50 indica un grado más fuerte de relación lineal que uno de r = .40. Su valor oscila entre -1 (correlación negativa perfecta) y +1 (correlación positiva perfecta).

Si el coeficiente es, digamos, .80 o .95, representa una correlación fuerte, significativa y positiva, es decir, las variables correspondientes se mueven o varían en la misma dirección. En cambio, si fuera -.80 o -.95, “x” e “y” se mueven o varían en direcciones opuestas. Un valor más cercano a 0 refleja la ausencia de asociación lineal. Una correlación baja [-0.2, 0.2] sugiere que gran parte de la variación de la variable de respuesta (y) no está explicada por el predictor (x) y debemos buscar mejores variables predictoras u otro modelo no lineal.

Observa que el coeficiente de correlación (0.5028585) es razonablemente bueno pero dista bastante de ser ideal, por lo que podemos continuar con nuestro estudio.

> model <- lm(Weight ~ Height, data = weightHeight)
> summary(model)

Call:
lm(formula = Weight ~ Height, data = weightHeight)

Residuals:
    Min      1Q  Median      3Q     Max 
-40.302  -6.711  -0.052   6.814  39.093 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -82.57574    2.28022  -36.21   <2e-16 ***
Height        3.08348    0.03352   91.98   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 10.08 on 24998 degrees of freedom
Multiple R-squared:  0.2529,	Adjusted R-squared:  0.2528 
F-statistic:  8461 on 1 and 24998 DF,  p-value: < 2.2e-16

Se puede calcular una regresión lineal en R con el comando lm. El formato de la orden es el siguiente: lm([variable de respuesta o dependiente y] ~ [variables independientes o predictoras], data = [origen de datos]). Podemos ver los valores de la intersección de la línea de regresión y el eje de ordenadas, y la pendiente. Por lo tanto, la ecuación de la línea de regresión se puede escribir de la siguiente manera: Peso = -82.57574 + 3.08348 * Altura.

Una medida para determinar la bondad o calidad del modelo es el coeficiente de determinación o R². Para los modelos que se ajustan muy bien a los datos, R² está cerca de 1. Dicho con otras palabras, R² determina la calidad del modelo para replicar o predecir los resultados y la proporción de la variación de los resultados que puede explicarse por el modelo. Por otro lado, los modelos que se ajustan mal a los datos tienen R² cercano a 0. En nuestro ejemplo, el modelo solo explica el 25,28% de la variabilidad de los datos. El estadístico F 8461 nos da la significación conjunta del modelo y produce un valor p del modelo <2.2e-16 que es significativo.

Los p-value de las variables predictoras individuales (columna del extremo derecho en la sección “Coeficientes”) son muy importantes. Cuando hay un p-value o valor p, hay una hipótesis nula y alternativa asociada a él. La hipótesis nula H₀ es que el coeficiente asociado con la variable predictora es cero (es decir, no hay relación entre “x” e “y”). La hipótesis alternativa H_a es que el coeficiente asociado es diferente de cero (es decir, existe alguna relación entre “x” e “y”). En nuestro ejemplo, tanto los valores p para la intersección de la línea de regresión y el eje de ordenadas como la altura (la variable predictora) son significativas, por lo que podemos rechazar la hipótesis nula, existe una relación significativa lineal entre el predictor (altura) y la variable de resultado (peso).

Los residuos del modelo de regresión lineal son la diferencia entre los datos observados de la variable dependiente “y” y los valores ajustados ŷ (los valores de respuesta predichos por el modelo). Podemos visualizarlos con la orden: plot(model$residuals)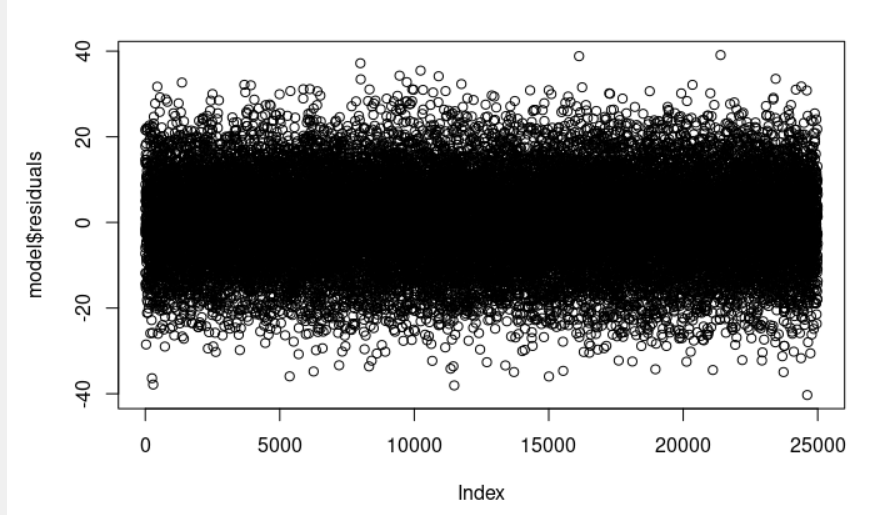

Observa que la sección residuals, residuos (model <- lm(Weight ~ Height, data = weightHeight), summary(model)) proporciona una visualización rápida de la distribución de los residuos. La mediana (-0.052) es cercana a cero, y los valores mínimo y máximo son aproximadamente iguales en valor absoluto (-40.302, 39.093).

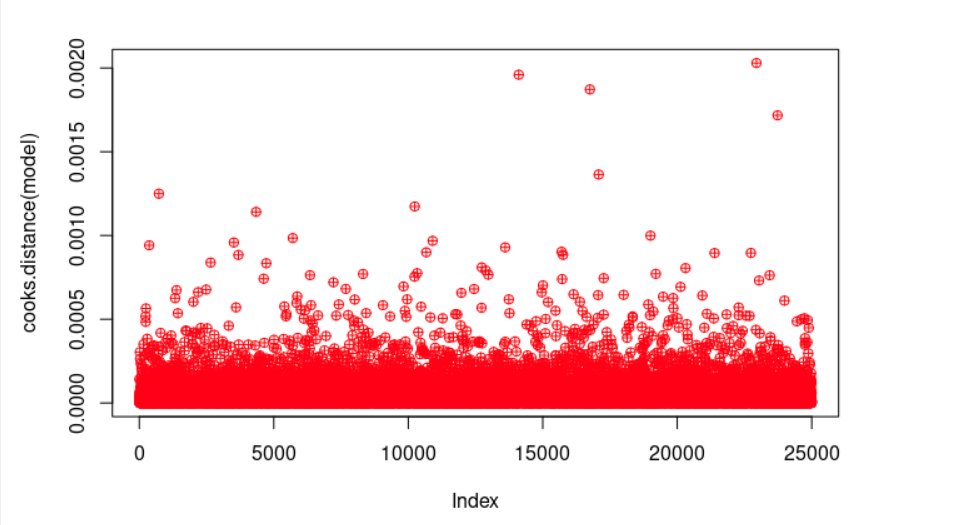
plot(cooks.distance(model), pch = 10, col = "red") # La distancia de Cook se usa en el análisis de regresión para identificar puntos influyentes y valores atípicos. Es una forma de encontrar aquellas observaciones que afectan negativamente al modelo de regresión. Con la orden plot los dibujamos.
cook <- cooks.distance(model)
significantValues <- cook > 1 # Como regla general, los casos con una distancia de Cook superior a uno deben investigarse más a fondo.
significantValues ​​# Afortunadamente, no obtenemos ninguno de esos puntos.

Regresión lineal múltiple

La regresión lineal múltiple es una generalización de la regresión lineal simple en el que se utiliza varias variables explicativas (predictoras o variables independientes) para predecir el resultado de una variable de respuesta o dependiente.

Su ecuación general es *y = b₀ + b₁x₁ + b₂x₂ + b₃x3 + … + + b_nx_n +e donde y es la variable de respuesta o dependiente, xi son las variables predictoras, independientes o explicativas, b₀ es la intersección de la línea de regresión y el eje de ordenada (el valor predicho cuando todas las variables xi=0), b₁ es el coeficiente de regresión de la primera variable independiente x₁,… b_n es el coeficiente de regresión de la última variable independiente x_n y e es el término de error o el error residual, es decir, la parte de la variable de respuesta que el modelo de regresión no puede explicar.

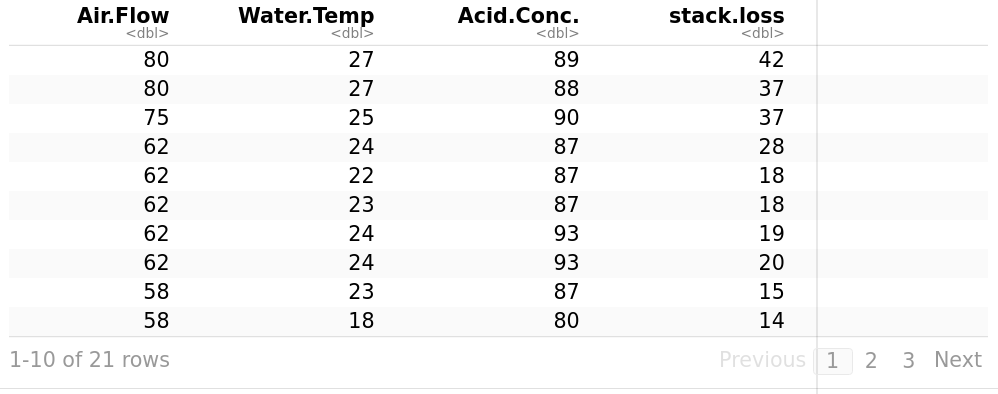
Hacemos uso de stackloss. Se describe como datos operativos de una planta para la oxidación de amoniaco a ácido nítrico. stack.loss es la variable dependiente y es el porcentaje del amoniaco entrante a la planta que escapa de la columna de absorción sin ser absorbido; es decir, una medida (inversa) de la eficiencia global de la planta. Air.Flow es el flujo de aire de refrigeración. Representa la tasa de operación de la planta. Water.Temp es la temperatura del agua de refrigeración que circula a través de las bobinas en la torre de absorción.

> stackloss

library("ggpubr")
ggscatter(stackloss, x = "stack.loss", y = "Air.Flow", color = "Water.Temp" # Visualicemos nuestros datos, x e y son las variables a representar, también podemos añadir color a nuestros puntos de datos en función del segundo factor o variable explicativa (color = "Water.Temp")
          add = "reg.line", conf.int = TRUE, # add = "reg.line" indicamos que añada la recta de regresión y conf.int = TRUE, el intervalo de confianza.
          cor.coef = TRUE, cor.method = "pearson", # cor.coef = TRUE especificamos que también incluya el coeficiente de correlación y cor.method = "pearson" es el método que seleccionamos para calcular el coeficiente de correlación. 
          xlab = "stack.loss", ylab = "Air.Flow")

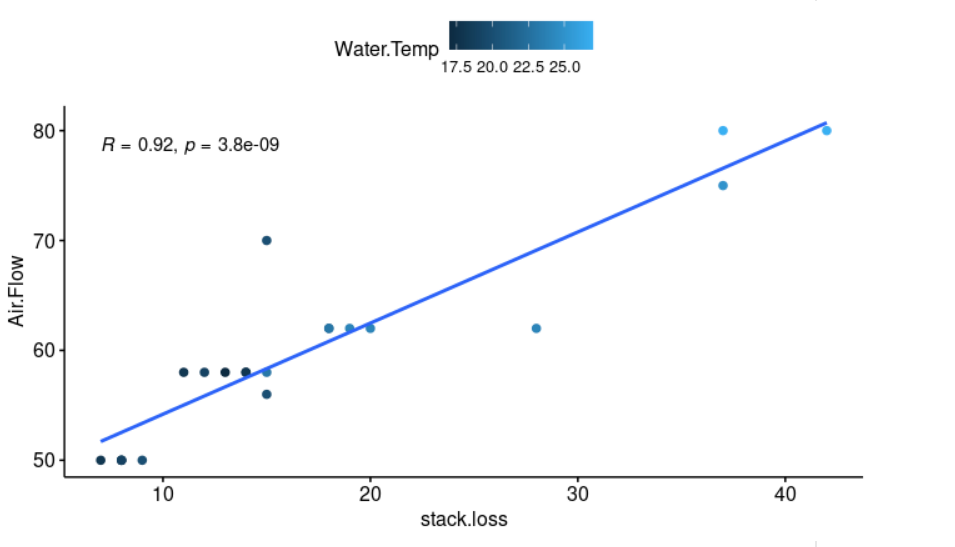
Se puede calcular una regresión lineal en R con el comando lm. El formato de la orden es el siguiente: lm ([variable de respuesta o dependiente y] ~ [variables predictoras o independientes], data = [origen o marco de datos]).

> model <- lm(stack.loss ~ Air.Flow + Water.Temp, data = stackloss)
> summary(model)

Call:
lm(formula = stack.loss ~ Air.Flow + Water.Temp, data = stackloss)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.5290 -1.7505  0.1894  2.1156  5.6588 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -50.3588     5.1383  -9.801 1.22e-08 ***
Air.Flow      0.6712     0.1267   5.298 4.90e-05 ***
Water.Temp    1.2954     0.3675   3.525  0.00242 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.239 on 18 degrees of freedom
Multiple R-squared:  0.9088,	Adjusted R-squared:  0.8986 
F-statistic: 89.64 on 2 and 18 DF,  p-value: 4.382e-10

La ecuación de la línea de regresión se puede escribir de la siguiente manera: stack.loss = -50.3588 + 0.6712*Air.Flow + 1.2954*Water.Temp.

Una medida para determinar la bondad o calidad del modelo es el coeficiente de determinación o R². Para los modelos que se ajustan muy bien a los datos, R² está cerca de 1. En el caso diametralmente opuesto, los modelos que se ajustan mal a los datos tienen R² cercano a 0. En nuestro ejemplo, el modelo explica el 89,86% de la variabilidad de los datos. En otras palabras, explica gran parte de la varianza en la variable dependiente. El estadístico F 89.64 nos da la significación conjunta del modelo y produce un valor p del modelo 4.382e-10 que es muy significativo.

Los p-value o valores p de las variables predictoras individuales (columna del extremo derecho en la sección “Coeficientes”) son muy importantes. Insisto, cuando hay un valor p, hay una hipótesis nula y una hipótesis alternativa asociada a él. La hipótesis nula H₀ es que los coeficientes asociados con las variables predictoras son iguales a cero (es decir, no hay relación -al menos, lineal- entre xi e y). La hipótesis alternativa H_a es que los coeficientes no son iguales a cero (es decir, existe relación entre xi e y). En nuestro ejemplo, los valores p para Intercept (la intersección de la línea de regresión y el eje de ordenada), Air.Flow y Water.Temp (las variables predictoras) son significativos, por lo que podemos rechazar la hipótesis nula, es decir, existe una relación lineal significativa entre los predictores (Air.Flow, Water.Temp) y la variable dependiente (stack.loss).

Los residuos del modelo de regresión lineal son la diferencia entre los datos observados de la variable dependiente “y” y los valores ajustados ŷ. Podemos trazarlos: plot(model$residuals) y deberían aparecer como puntos aleatorios; en otras palabras, sin mostrar un patrón o estructura evidente.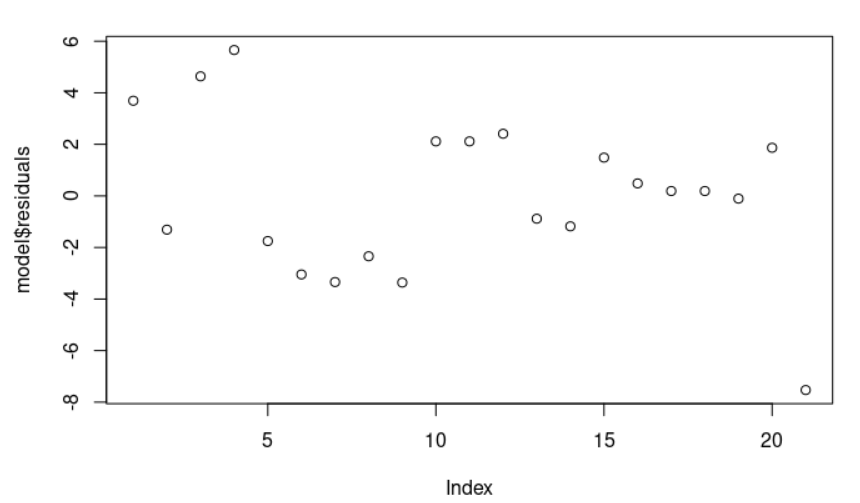

Observe que la sección Residuals, residuos (model <- lm(stack.loss ~ Air.Flow + Water.Temp, data = stackloss), summary(model)) proporciona una vista rápida de la distribución de los residuos. La mediana (0,1894) está cerca de cero, y los valores mínimo y máximo son similares en valor absoluto (-7,5290, 5,6588).

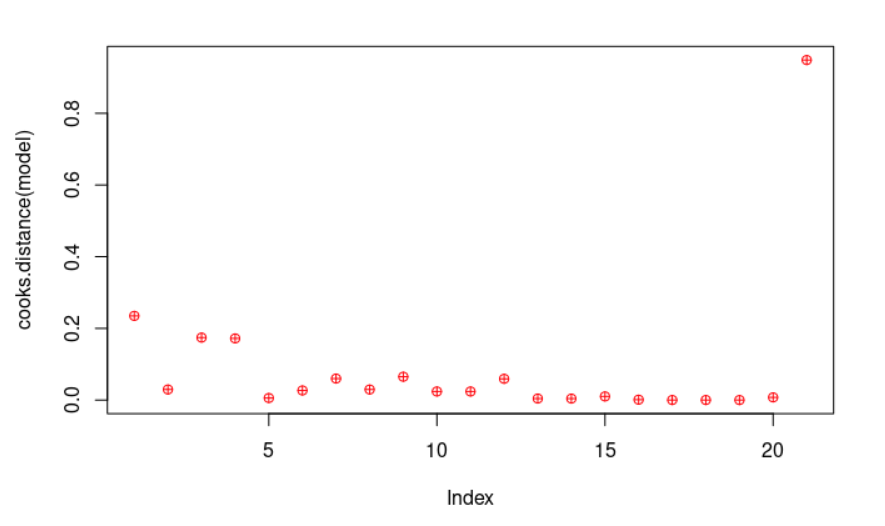
plot(cooks.distance(model), pch = 10, col = "red") # La distancia de Cook se utiliza en el análisis de regresión para encontrar puntos influyentes y valores atípicos. Es una forma de identificar observaciones que afectan negativamente al modelo de regresión. Con la orden plot los dibujamos.
significantValues <- cook > 1 # Como regla general, los casos con una distancia de Cook superior a uno deben investigarse más a fondo.
significantValues # Afortunadamente, no obtenemos ninguno de esos puntos.
1     2     3     4     5     6     7     8     9    10    11    12    13    14    15 
FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE 
   16    17    18    19    20    21 
FALSE FALSE FALSE FALSE FALSE FALSE

Veamos otro ejemplo de regresión lineal múltiple usando las observaciones Iris Data de Edgar Anderson.

> data(iris)

El conjunto de datos “iris” da las medidas en centímetros de las variables largo y ancho del sépalo, así como, largo y ancho del pétalo, respectivamente, para 50 flores de cada una de las tres especies de iris.

> summary(iris)
  Sepal.Length    Sepal.Width     Petal.Length    Petal.Width          Species  
 Min.   :4.300   Min.   :2.000   Min.   :1.000   Min.   :0.100   setosa    :50  
 1st Qu.:5.100   1st Qu.:2.800   1st Qu.:1.600   1st Qu.:0.300   versicolor:50  
 Median :5.800   Median :3.000   Median :4.350   Median :1.300   virginica :50  
 Mean   :5.843   Mean   :3.057   Mean   :3.758   Mean   :1.199                  
 3rd Qu.:6.400   3rd Qu.:3.300   3rd Qu.:5.100   3rd Qu.:1.800                  
 Max.   :7.900   Max.   :4.400   Max.   :6.900   Max.   :2.500                  
> model <- lm(Sepal.Length ~ Sepal.Width + Petal.Length + Petal.Width, data = iris)
> summary(model)

Call:
lm(formula = Sepal.Length ~ Sepal.Width + Petal.Length + Petal.Width, 
    data = iris)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.82816 -0.21989  0.01875  0.19709  0.84570 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)   1.85600    0.25078   7.401 9.85e-12 ***
Sepal.Width   0.65084    0.06665   9.765  < 2e-16 ***
Petal.Length  0.70913    0.05672  12.502  < 2e-16 ***
Petal.Width  -0.55648    0.12755  -4.363 2.41e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.3145 on 146 degrees of freedom
Multiple R-squared:  0.8586,	Adjusted R-squared:  0.8557 
F-statistic: 295.5 on 3 and 146 DF,  p-value: < 2.2e-16

> plot(model$residuals)

La ecuación de la línea de regresión se puede escribir de la siguiente manera: Sépalo.Longitud = 1.85600 + 0.65084 * Sépalo.Ancho + 0.70913 * Pétalo.Longitud + -0.55648 * Pétalo.Ancho. En este ejemplo, el modelo explica el 85,57% de la variabilidad de los datos (explica gran parte de la varianza en la variable dependiente, Sepal.Length). El estadístico F 295.5 nos da la significación conjunta del modelo y produce un valor p del modelo < 2.2e-16 que es muy significativo.

Tanto los valores p para el Intercept (la intersección de la línea de regresión y el eje de ordenada) como para las variables predictoras individuales (Ancho sépalo, Longitud del pétalo y Ancho del pétalo) son significativos. Como consecuencia, podemos rechazar la hipótesis nula y afirmar que existe una relación significativa lineal entre los predictores (Sepal.Width, Petal.Length y Petal.Width) y la variable de resultado (Sepal.Length).

Los datos residuales del modelo de regresión lineal son la diferencia entre los datos observados de la variable dependiente “y” y los valores ajustados ŷ. Podemos trazarlos: plot (model$residuals) y se nos aparecen distribuidos aleatoriamente, es decir, no se aprecia ningún patrón o estructura.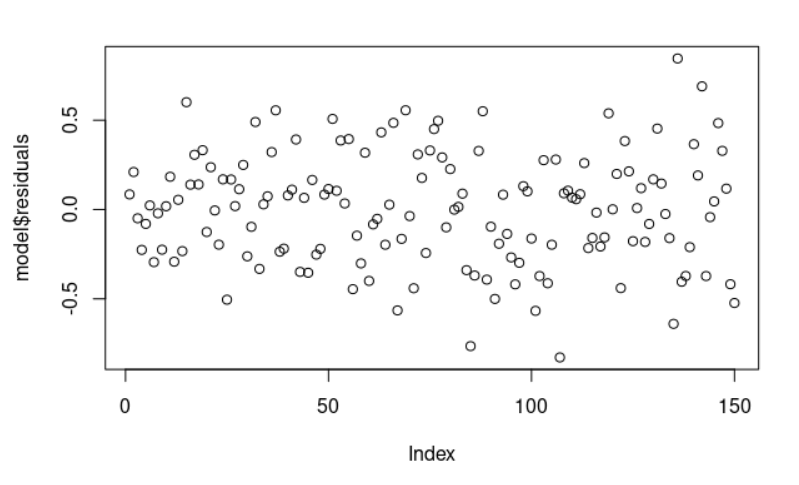

Finalmente, veamos un tercer y último ejemplo de regresión lineal múltiple utilizando el conjunto de datos “trees”, árboles. Proporciona medidas del diámetro del árbol en pulgadas (tiene la etiqueta Girth), la altura y el volumen de la madera en pies cúbicos de 31 cerezos negros talados.

> summary(trees)
     Girth           Height       Volume     
 Min.   : 8.30   Min.   :63   Min.   :10.20  
 1st Qu.:11.05   1st Qu.:72   1st Qu.:19.40  
 Median :12.90   Median :76   Median :24.20  
 Mean   :13.25   Mean   :76   Mean   :30.17  
 3rd Qu.:15.25   3rd Qu.:80   3rd Qu.:37.30  
 Max.   :20.60   Max.   :87   Max.   :77.00  
> model <- lm(Volume ~ Girth + Height, data = trees)
> summary(model)

Call:
lm(formula = Volume ~ Girth + Height, data = trees)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.4065 -2.6493 -0.2876  2.2003  8.4847 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -57.9877     8.6382  -6.713 2.75e-07 ***
Girth         4.7082     0.2643  17.816  < 2e-16 ***
Height        0.3393     0.1302   2.607   0.0145 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.882 on 28 degrees of freedom
Multiple R-squared:  0.948,	Adjusted R-squared:  0.9442 
F-statistic:   255 on 2 and 28 DF,  p-value: < 2.2e-16

La ecuación de la recta de regresión se puede escribir de la siguiente manera: Volume = -57.9877 + 4.7082*Girth + 0.3393*Height. En este ejemplo, el modelo explica el 94,42% de la variabilidad de los datos, es decir, explica la mayor parte de la varianza en la variable dependiente, Volumen. El estadístico F 255, como ya sabemos, nos da la significación conjunta del modelo y produce un valor p del modelo < 2.2e-16 que es muy significativo.

Tanto los valores p para el Intercept (la intersección de la línea de regresión y el eje de ordenada) como para las variables predictoras individuales (Diámetro y Altura) son significativos, por lo que podemos rechazar la hipótesis nula, existe una relación lineal significativa entre los predictores (Diámetro y Altura) y la variable de resultado (Volumen).