Symmetry Groups

The difference between a successful person and others is not a lack of strength, not a lack of knowledge, but rather is a lack or will. […] The price of success is hard work, dedication to the job at hand, and the determination that whether we win or lose, we have applied the best of ourselves to the task at hand, Vince Lombardi.

Definition. An isometry of a n-dimensional space Rⁿ is a distance-preserving map Φ from ℝⁿ onto itself, that is, ∀p, q ∈ ℝⁿ, the distance from Φ(p) to Φ(q) is the same as the distance from p to q, i.e., d(p, q) = d(Φ(p), Φ(q)) where d is a metric on ℝⁿ.

Let F be a set of points in ℝⁿ. The symmetry group of F in ℝⁿ is the set of all isometries of ℝⁿ that carry F onto itself under function composition.

Examples:

• Consider the line segment I in ℝ from a = 0 to b = 1. There are two isometries which map I onto itself, namely f(x) = x and g(x) = 1 -x. Observe the multiplication table for the symmetry group (Figure 1.a.). It has order 2. D₁ ≋ ℤ₂, the cyclic group of order 2.  
• Consider the line segment I in ℝ² from a = (0, 0) to b = (1, 0). There are four isometries which map I onto itself, namely: f₀(x, y) = (x, y), the identity; f₁(x, y) = (1-x, y), reflection about the line x = 1/2; f₂(x, y) = (x, -y), reflection about the line y = 0; and f₃(x, y) = (1-x, -y), a combination of both f₁ and f₂.

Observe the multiplication table for the symmetry group (Figure 1.b.). The group is denoted as ⟨D₂, ○⟩. It has order 4. D₂ ≋ K4, the Klein four-group, the smallest non-cyclic group.

• We have also studied the group of symmetries of an equilateral triangle, the dihedral group D₃. It contains a subgroup of order 3, {e = id, r = ρ₁, r² = ρ₂} ≤ D₃, Figure 1.c.  

Classification of isometries

It can be shown that there are four types of Euclidean plane isometries:

• Translations, denoted by T_v where v is a vector in ℝ² have the effect of shifting or carrying all points in the direction of v. (Figure 1.e) ∀p ∈ ℝ², T_v(p) = p + v = $(\begin{smallmatrix}p_x+v_x\\ p_y+v_y\end{smallmatrix})$. A translation can be interpreted as a composite of two parallel reflections.  
• Rotations, denoted by R_c,θ, where c is a point in the plane called the center of the rotation, and θ is the angle of rotation (Figure 1.d).

1. A rotation around the origin is given by, R_0,θ(p) = $(\begin{smallmatrix}cosθ & -sinθ\\ sinθ & cosθ\end{smallmatrix})(\begin{smallmatrix}p_x\\ p_y\end{smallmatrix})$
2. A rotation around a point c can be accomplished by first translating c to the origin, then performing the rotation around the origin, and finally translating the origin back to c, that is, R_c,θ(p) = T_c ∘ R_0,θ ∘ T_-c(p) = c + R_0,θ(p-c)  

• Reflections or mirror isometries, denoted by F_c,v where c is a point in the plane and v is a unit vector in ℝ² have the effect of reflecting the point p in the line L that is perpendicular to v and that passes through c. L acts like a two-sided mirror, e.g., a clockwise spiral is reflected as a counterclockwise spiral, a right hand as a left hand, and so on.

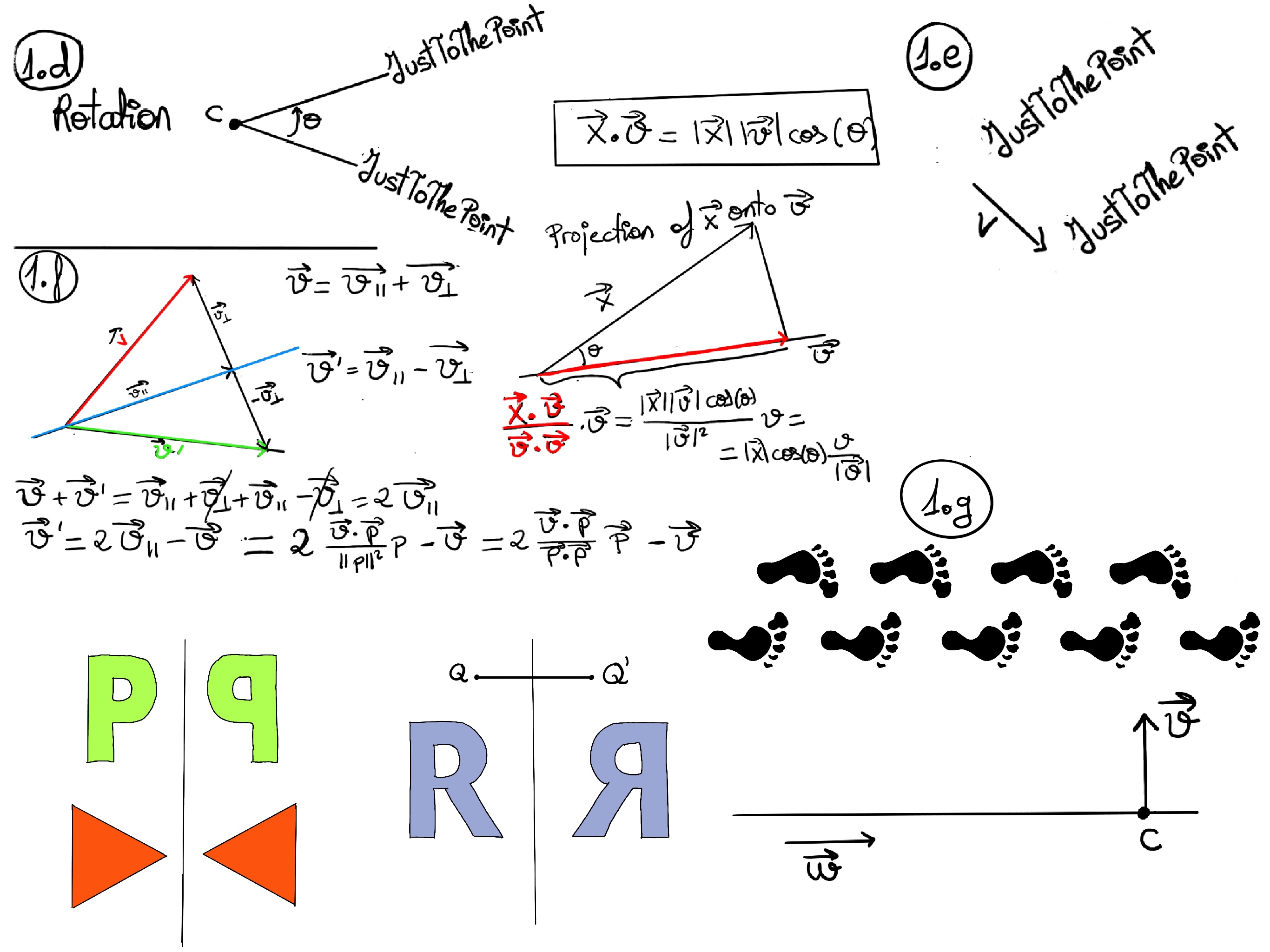
Let v’ be the reflection of a vector v through the blue line in the figure below (Figure 1.f.). We form two mirror-image right triangles.

1. The triangle with v as hypotenuse shows v as the sum of two vectors, v = v_∥ + v_⊥ where v_∥ is a component parallel to the line of reflection (the projection of v onto the line of reflection) and v_⊥ is a component perpendicular to the line.
2. The second triangle has v’ as hypotenuse, it shows v’ as the vector difference, v’ = v_∥ - v_⊥.

If we add v and its reflection, v + v’ = (v_∥ + v_⊥) + (v_∥ - v_⊥) = 2v_∥ ⇒ v’ = 2v_∥ -v = $2\frac{v·p}{p·p}p-v$

Notice that the projection of a vector x onto v (In our particular case, v_∥ onto p, where p is any non-zero vector parallel to the line of reflection) is defined as

$\frac{x.v}{v·v}v=\frac{|x||v|cos(θ)}{|v|^2}v=|x|cos(θ)\frac{v}{|v|}$ because this vector has length |x|cosθ -recall that v is a unit vector- and its points in the direction of v, which is what we were looking for.

Recall that x·v = |x||v|cos(θ)

• A glide reflections consists of a reflection over a line and then translation along the same line, both combined into a single operation (Figure 1.g.). It is denoted by G_c,v,w, where c is a point in the plane, v is a unit vector in ℝ², and w is a non-null vector perpendicular to v. Therefore, G_c,v,w(p) = T_w ∘ F_c,v(p) = w + F_c,v(p).

  A glide reflection is a composition of a reflection in the line described by c and v (F_c,v) and a translation along w.

   

Recall that the group of symmetries of a regular polygon with n sides contains the n rotations {r_θ, θ = 2πk/n, k = 0,…, n-1} = ⟨r_2π/n⟩ together with some mirror reflections. We center this regular n-sided polygon at (0, 0) with one vertex at (1, 0) and label its vertices by the nth roots of unity: 1, w, w², …, w^n-1, where w=e^i2π/n (Figure 1.a.), all rotations can be written in the generic form of planar isometries as H(z)=αz, α = w^k = e^i2πk/n, k = 0,…, n-1  

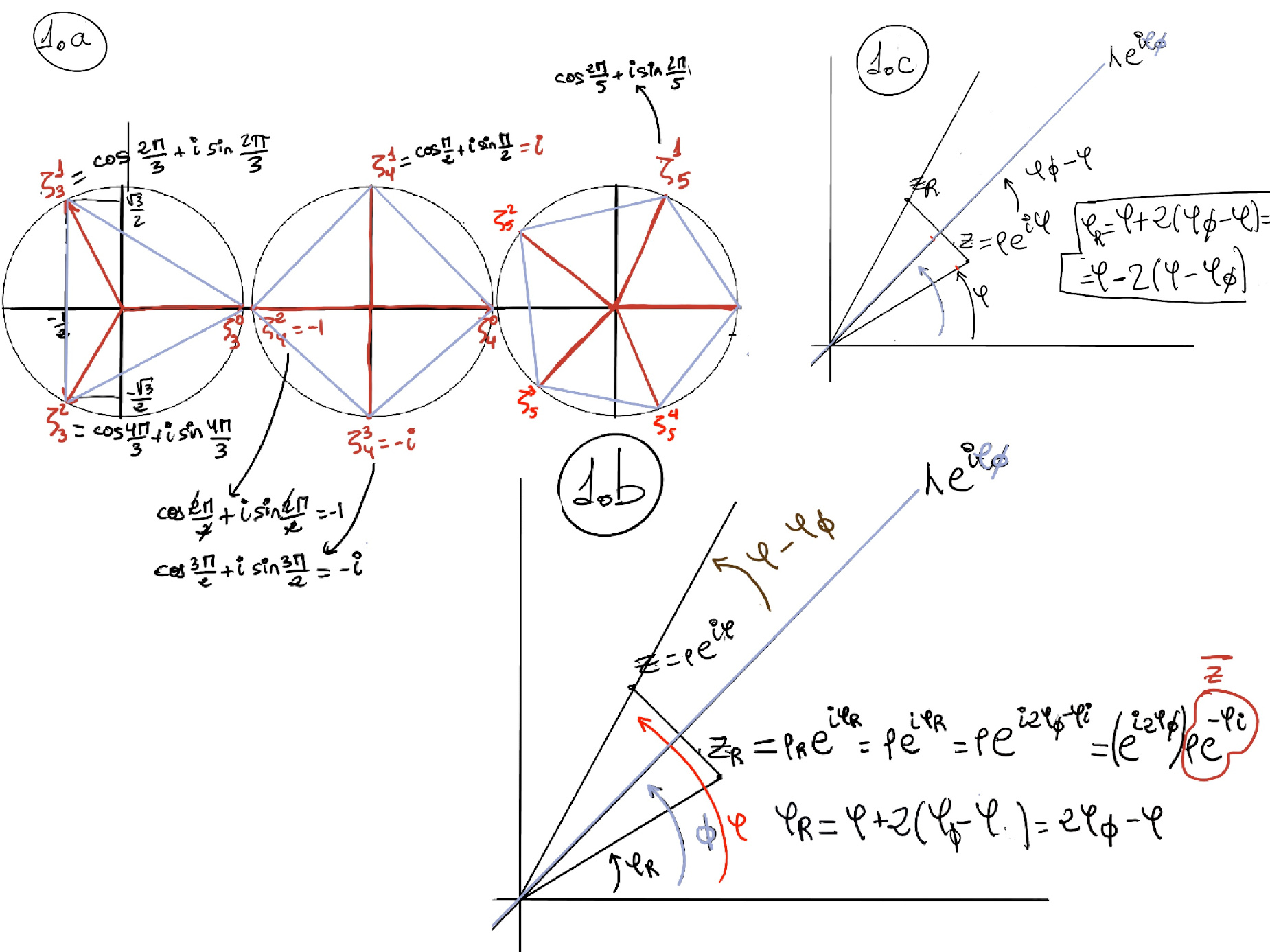
Let’s consider mirror reflections about a line l passing through (0, 0) at an angle Φ₀, defined by l(λ) = λe^iΦ₀. We want to reflect a complex number, say z = ρe^iΦ, about the line l. Let us write z_R = ρ_Re^iΦ_R as the complex number z after being reflected. Since a reflection is an isometry and isometries are distance preserving maps, ρ_R = ρ.

Futhermore, suppose that Φ_R ≤ Φ₀ (Figure 1.b.) ⇒ Φ_R = Φ +2(Φ₀ -Φ). If Φ_R ≥ Φ₀ (Figure 1.c) ⇒ Φ_R = Φ - 2(Φ - Φ₀). And therefore, in both cases, Φ_R = 2Φ₀ -Φ, and z_R = ρ_Re^iΦ_R = ρe^iΦ_R = ρ^{ei2Φ₀ -Φi} = ρ^ei2Φ₀ρe^-Φi = ρ^ei2Φ₀$\bar z$  

Theorem. Any planar isometry is either a rotation, a translation, a reflection about a line in the plane, or a reflection about a line in the plane and a translation along the same line (glide reflection)

Every isometry in ℝ² can be written as H:ℂ → ℂ, H(z) = αz + β or H(z) = α$\bar z + β$, |α| = 1.

• If α = 1, β = 0, H(z) = z, the identity map.
• If α = 1, β ≠ 0, H(z) = z + β, there is no fixed point, this isometry is a translation.
• If α ≠ 1, then H(z) = [fixed point] z = αz + β ⇒ z - αz = β ⇒ z = $\frac{β}{1-α}$, and

$H(z)-\frac{β}{1-α}=αz + (β -\frac{β}{1-α})=αz+\frac{β-βα-β}{1-α}=α(z-\frac{β}{1-α})⇒H(z)=α(z-\frac{β}{1-α})+\frac{β}{1-α}$ Basically, we translate the fixed point to the origin, rotate, and translate back, that is, a rotation about the fixed point $\frac{β}{1-α}$

• If H(z) = $α\bar z+β$, we can write this isometry as

$(\begin{smallmatrix}x’\\ y’\end{smallmatrix})=(\begin{smallmatrix}cosθ & sinθ\\ sinθ & -cosθ\end{smallmatrix})(\begin{smallmatrix}x\\ y\end{smallmatrix})+(\begin{smallmatrix}t_1\\ t_2\end{smallmatrix})$. A fixed point (x_F, y_F) satisfy the following equation,

$(\begin{smallmatrix}x_F\\ y_F\end{smallmatrix})=(\begin{smallmatrix}cosθ & sinθ\\ sinθ & -cosθ\end{smallmatrix})(\begin{smallmatrix}x_F\\ y_F\end{smallmatrix})+(\begin{smallmatrix}t_1\\ t_2\end{smallmatrix}) ↭ (\begin{smallmatrix}1 & 0\\ 0 & 1\end{smallmatrix})(\begin{smallmatrix}x_F\\ y_F\end{smallmatrix})=(\begin{smallmatrix}cosθ & sinθ\\ sinθ & -cosθ\end{smallmatrix})(\begin{smallmatrix}x_F\\ y_F\end{smallmatrix})+(\begin{smallmatrix}t_1\\ t_2\end{smallmatrix})$ ↭ $(\begin{smallmatrix}1-cosθ & -sinθ\\ -sinθ & 1+cosθ\end{smallmatrix})(\begin{smallmatrix}x_F\\ y_F\end{smallmatrix})=(\begin{smallmatrix}t_1\\ t_2\end{smallmatrix})$

$det(M)=det(\begin{smallmatrix}1-cosθ & -sinθ\\ -sinθ & 1+cosθ\end{smallmatrix}) = (1-cos(θ))(1+cos(θ))-sin^2θ=1 -cos^2θ-sin^2θ=0$

This matrix M can be rewritten as, $(\begin{smallmatrix}2sin\frac{θ}{2}sin\frac{θ}{2} & -2sin\frac{θ}{2}cos\frac{θ}{2}\\ -2sin\frac{θ}{2}cos\frac{θ}{2} & 2cos\frac{θ}{2}cos\frac{θ}{2}\end{smallmatrix})=2(\begin{smallmatrix}sin\frac{θ}{2}\\ -cos\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}sin\frac{θ}{2} & -cos\frac{θ}{2}\end{smallmatrix})$

sin(2θ) = 2sinθcosθ, sin(θ) = 2sin(θ/2)cos(θ/2)

Therefore, fixed points (x_F, y_F) have to be solutions of, $2(\begin{smallmatrix}sin\frac{θ}{2}\\ -cos\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}sin\frac{θ}{2} & -cos\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}x_F\\ y_F\end{smallmatrix})=(\begin{smallmatrix}t_1\\ t_2\end{smallmatrix})$

If $[t_1, t_2]=λ[sin(\frac{θ}{2}), -cos(\frac{θ}{2})]$

$2(\begin{smallmatrix}sin\frac{θ}{2}\\ -cos\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}sin\frac{θ}{2} & -cos\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}x_F\\ y_F\end{smallmatrix})=λ(\begin{smallmatrix}sin(\frac{θ}{2})\\ -cos(\frac{θ}{2})\end{smallmatrix})↭2(\begin{smallmatrix}sin\frac{θ}{2} & -cos\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}x_F\\ y_F\end{smallmatrix})=λ↭x_Fsin(\frac{θ}{2})-y_Fcos(\frac{θ}{2})=\frac{λ}{2}$, that is, (x_F, y_F) forms a line.

$(\begin{smallmatrix}x’\\ y’\end{smallmatrix})=(\begin{smallmatrix}cos^2\frac{θ}{2}-sin^2\frac{θ}{2} & 2sin\frac{θ}{2}cos\frac{θ}{2}\\ 2sin\frac{θ}{2}cos\frac{θ}{2} & -cos^2\frac{θ}{2}+sin^2\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}x\\ y\end{smallmatrix})+λ(\begin{smallmatrix}sin\frac{θ}{2}\\ -cos\frac{θ}{2}\end{smallmatrix})=(\begin{smallmatrix}cos\frac{θ}{2} & sin\frac{θ}{2}\\ sin\frac{θ}{2} & -cos\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}1 & 0\\ 0 & -1\end{smallmatrix})(\begin{smallmatrix}cos\frac{θ}{2} & sin\frac{θ}{2}\\ sin\frac{θ}{2} & -cos\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}x\\ y\end{smallmatrix})+λ(\begin{smallmatrix}sin\frac{θ}{2}\\ -cos\frac{θ}{2}\end{smallmatrix})$

Multiplying both side by the rotation $(\begin{smallmatrix}cos\frac{θ}{2} & sin\frac{θ}{2}\\ sin\frac{θ}{2} & -cos\frac{θ}{2}\end{smallmatrix})$

$(\begin{smallmatrix}cos\frac{θ}{2} & sin\frac{θ}{2}\\ sin\frac{θ}{2} & -cos\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}x’\\ y’\end{smallmatrix})=(\begin{smallmatrix}1 & 0\\ 0 & -1\end{smallmatrix})(\begin{smallmatrix}cos\frac{θ}{2} & sin\frac{θ}{2}\\ sin\frac{θ}{2} & -cos\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}x\\ y\end{smallmatrix})+λ(\begin{smallmatrix}0\\ 1\end{smallmatrix})$

In the rotated coordinates $(\begin{smallmatrix}\bar x’\\ \bar y’\end{smallmatrix})=(\begin{smallmatrix}cos\frac{θ}{2} & sin\frac{θ}{2}\\ sin\frac{θ}{2} & -cos\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}x’\\ y’\end{smallmatrix})$ and $(\begin{smallmatrix}\bar x\\ \bar y\end{smallmatrix})=(\begin{smallmatrix}cos\frac{θ}{2} & sin\frac{θ}{2}\\ sin\frac{θ}{2} & -cos\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}x\\ y\end{smallmatrix})$, we have $(\begin{smallmatrix}\bar x’\\ \bar y’\end{smallmatrix})=(\begin{smallmatrix}1 & 0\\ 0 & -1\end{smallmatrix})(\begin{smallmatrix}\bar x\\ \bar y\end{smallmatrix})+λ(\begin{smallmatrix}0\\ 1\end{smallmatrix})$ ⇒ $\bar x’=\bar x,~ \bar y’= -\bar y+λ↭\bar x’=\bar x,~ (\bar y’-\frac{λ}{2})=-(\bar y-\frac{λ}{2})$. Therefore, in the rotated coordinates this isometry is a reflection about the line y =λ/2

If $[t_1, t_2]≠λ[sin(\frac{θ}{2}), -cos(\frac{θ}{2})]$, then we have no fixed points. Following the same argument,

$(\begin{smallmatrix}x’\\ y’\end{smallmatrix})=(\begin{smallmatrix}cos^2\frac{θ}{2}-sin^2\frac{θ}{2} & 2sin\frac{θ}{2}cos\frac{θ}{2}\\ 2sin\frac{θ}{2}cos\frac{θ}{2} & -cos^2\frac{θ}{2}+sin^2\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}x\\ y\end{smallmatrix})+(\begin{smallmatrix}t_1\\ t_2\end{smallmatrix})=(\begin{smallmatrix}cos\frac{θ}{2} & sin\frac{θ}{2}\\ sin\frac{θ}{2} & -cos\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}1 & 0\\ 0 & -1\end{smallmatrix})(\begin{smallmatrix}cos\frac{θ}{2} & sin\frac{θ}{2}\\ sin\frac{θ}{2} & -cos\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}x\\ y\end{smallmatrix})+(\begin{smallmatrix}t_1\\ t_2\end{smallmatrix})$

Multiplying both side by the rotation $(\begin{smallmatrix}cos\frac{θ}{2} & sin\frac{θ}{2}\\ sin\frac{θ}{2} & -cos\frac{θ}{2}\end{smallmatrix})$

$(\begin{smallmatrix}cos\frac{θ}{2} & sin\frac{θ}{2}\\ sin\frac{θ}{2} & -cos\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}x’\\ y’\end{smallmatrix})=(\begin{smallmatrix}1 & 0\\ 0 & -1\end{smallmatrix})(\begin{smallmatrix}cos\frac{θ}{2} & sin\frac{θ}{2}\\ sin\frac{θ}{2} & -cos\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}x\\ y\end{smallmatrix})+(\begin{smallmatrix}cos\frac{θ}{2} & sin\frac{θ}{2}\\ sin\frac{θ}{2} & -cos\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}t_1\\ t_2\end{smallmatrix})$

And we have as before in the rotated coordinates,

$(\begin{smallmatrix}\bar x’\\ \bar y’\end{smallmatrix})=(\begin{smallmatrix}1 & 0\\ 0 & -1\end{smallmatrix})(\begin{smallmatrix}\bar x\\ \bar y\end{smallmatrix})+(\begin{smallmatrix}cos\frac{θ}{2} & sin\frac{θ}{2}\\ sin\frac{θ}{2} & -cos\frac{θ}{2}\end{smallmatrix})(\begin{smallmatrix}t_1 \\ t_2\end{smallmatrix})=(\begin{smallmatrix}1 & 0\\ 0 & -1\end{smallmatrix})(\begin{smallmatrix}\bar x\\ \bar y\end{smallmatrix})+(\begin{smallmatrix}m \\ n\end{smallmatrix})$

$\bar x’=\bar x+m, (\bar y’-\frac{n}{2})=-(\bar y-\frac{n}{2})$. Therefore, $\bar x’=\bar x+m$ is a translation along the direction of the reflection line (consider that $\bar x’~ and~ \bar x$ are rotated coordinated, then it is a translation along the direction of the reflection line) and a reflection about the line y=n/2.

Theorem. Every finite group G of isometries of the plane is isomorphic to either ℤ_n or to a dihedral group D_n for some positive integer n.

Proof.

Let G be a finite group of isometries of the plane. G = {Φ₁, Φ₂,…, Φ_n}. This means that for every Φ_k, ⟨Φ_k⟩ is finite, that there exists Φ_k^-1, and that Φ_k∘Φ_t = Φ_s ∈ G. What are all the isometries that could be in this finite group? Recall all the isometries of the plane: translations, rotations, reflections, and glide reflections.

• Φ_k cannot be a translation. A translation T(β) is defined by T(β): z → z + β, thus, T(β₂)∘T(β₁) = (z + β₁) + β₂ = z + β₁ + β₂ = T(β₁ + β₂), and translations form a subgroup of the planar isometries that is isomorphic to (ℂ, +) or (ℝ², +). The isomorphism Φ is given by Φ: T(β) → β.

Observe that ⟨Φ_k⟩ = {Φ_kⁿ, n ∈ ℤ}, and therefore, a translation generates an infinite subgroup. Thus, translations cannot belong to a finite group.

• Φ_k cannot be a glide reflection, since Φ_k∘Φ_k is a translation, then ⟨Φ_k²⟩ is not a finite set ⊥

• Could it be a rotation? To define a rotation, we fix a center, say the origin, around which we rotate (counter-clockwise). R(θ): z → e^θiz. In general, we take a rotation around a point different than 0, say z₀, R_Ω(θ) = [Ω = z₀] R_z0(θ): z → e^θi(z-z₀) + z₀.

  First, translate z₀ to the origin, then rotate, then move back to z₀.

Therefore, a composition of rotations about a center Ω, R_Ω(θ₂) ∘ R_Ω(θ₁) = e^iθ₂(e^iθ₁(z - z₀) + z₀ -z₀) + z₀ = e^{i(θ₁+θ₂)}(z - z₀) + z₀ = R_Ω(θ₁ + θ₂) which shows that rotations about a given fixed center Ω (= z₀) form a subgroup of planar isometries.

Let’s now consider the composition of two rotations about different centers.

R_Ω1(θ₁) = e^iθ₁(z -z₁) + z₁, R_Ω2(θ₂) = e^iθ₂(z -z₂) + z₂, so that

R_Ω2(θ₂) ∘ R_Ω1(θ₁) = e^iθ₂(e^iθ₁(z -z₁) + z₁ - z₂) + z₂ = e^{i(θ₂+θ₁)}(z - z₁) + e^iθ₂(z₁ -z₂) + z₂ = e^{i(θ₁+θ₂)}(z - γ) + γ

-e^{i(θ₁+θ₂)}z₁ + e^iθ₂(z₁ -z₂) + z₂ = -e^{i(θ₁+θ₂)}γ + γ

-e^{i(θ₁+θ₂)}z₁ + e^iθ₂z₁ -e^iθ₂z₂ + z₂ = -e^{i(θ₁+θ₂)}γ + γ

(1 - e^{i(θ₁+θ₂)})γ = z₂ + e^iθ₂(z₁ - z₂) -e^{i(θ₁+θ₂)}z₁

γ = ^{z₂ + eiθ₂(z₁ - z₂) -ei(θ₁+θ₂)z₁}⁄_{1 - e^i(θ1+θ2)}

In conclusion, we have a rotation by (θ₁ + θ₂), that is, R_Ω2(θ₂) ∘ R_Ω1(θ₁) = e^{i(θ₁+θ₂)}(z - γ) + γ, around a new center γ

If z₁ ≠ z₂ and θ₂=-θ₁, R_Ω2(-θ₁) ∘ R_Ω1(θ₁) =[In general] e^{i(θ₂+θ₁)}(z - z₁) + e^iθ₂(z₁ -z₂) + z₂ =[θ₂=-θ₁] z - z₁ -e^iθ₁(z₁ -z₂) + z₂ = z + (z₁ -z₂)(e^-iθ₁ -1), that is, just a translation, so it is not possible.

Futhermore, if both $R_{Ω_1}(θ_1)$ and $R_{Ω_2}(θ_2)$ are in a finite group, then both their compositions and their inverses must be there, too.

$R_{Ω_2}(θ_2)∘R_{Ω_1}(θ_1)=$ e^{i(θ₂+θ₁)}(z - z₁) + e^iθ₂(z₁ -z₂) + z₂ = e^{i(θ₂+θ₁)}z -e^{i(θ₂+θ₁)}z₁ + e^iθ₂(z₁ -z₂) + z₂

$R_{Ω_2}^{-1}(θ_2)∘R_{Ω_1}^{-1}(θ_1)=$ e^{-i(θ₂+θ₁)}(z - z₁) + e^-iθ₂(z₁ -z₂) + z₂ = e^{-i(θ₂+θ₁)}z -e^{-i(θ₂+θ₁)}z₁ + e^-iθ₂(z₁ -z₂) + z₂

$R_{Ω_2}(-θ_2)∘R_{Ω_1}(-θ_1)∘R_{Ω_2}(θ_2)∘R_{Ω_1}(θ_1)=$ e^{-i(θ₂+θ₁)}[e^{i(θ₂+θ₁)}z -e^{i(θ₂+θ₁)}z₁ + e^iθ₂(z₁ -z₂) + z₂] -e^{-i(θ₂+θ₁)}z₁ + e^-iθ₂(z₁ -z₂) + z₂ = z -z₁ + e^-iθ₁(z₁-z₂) +e^{-i(θ₂+θ₁)}z₂ -e^{-i(θ₂+θ₁)}z₁ + e^-iθ₂(z₁ -z₂) + z₂ = z + (z₂-z₁) + e^{-i(θ₂+θ₁)}(z₂-z₁) -(z₂-z₁)(e^-iθ₁ + e^-iθ₂) = z + (z₂-z₁)[1 + e^{-i(θ₂+θ₁)} -(e^-iθ₂ + e^-iθ₁)], a pure translation if z₁≠z₂, that is, rotations about different centers cannot be included.

Among the planar isometries, so far, only rotations with same center are allow.

So we are left with reflections and glide reflections about a line l. Suppose we have two reflections or two glide reflections (composition with a translation, say β₁ and β₂) of the form,

Φ₁: z → $e^{iθ_1}\bar z+β_1$, Φ₂: z → $e^{iθ_2}\bar z+β_2$

Φ₂∘Φ₁(z)=$e^{iθ_2}\overline {(e^{iθ_1}\bar z + β_1)}+β_2=e^{i(θ_2-θ_1)}z+\bar β_1e^{iθ_2}+β_2$

If θ₂ = θ₁ = θ, Φ₂∘Φ₁(z) = z +$\bar β_1e^{iθ}+β_2$, we get a translation, where $\bar β_1e^{iθ}+β_2$ is the translation vector. This is happening when the lines defining the reflections and glide reflections are parallel. They reflect a shape with respect to a line, and then again with respect to another line parallel to the first one, and basically you will get the shape being translated in the direction perpendicular to both lines.

If instead θ₂-θ₁≠0, we get a rotation, since the composition Φ₂∘Φ₁(z) will have one well defined fixed point,

z_FP =$ e^{i(θ_2-θ_1)}z_{FP}+\bar β_1e^{iθ_2}+β_2$ ⇒ $z_{FP} = \frac{\bar β_1e^{iθ_2}+β_2}{1-e^{i(θ_2-θ_1)}}$

Therefore, we can have:

1. Rotations which must all have the same center Ω
2. Reflections, but their lines cannot be parallel (they produce translations) and they must intersect at Ω. Otherwise, they would be able to produce rotations about points different from Ω and hence produce translations.

Let us look at the rotations about Ω in G and list the rotation angles in increasing order: θ₁ < θ₂ < ··· < θ_l-1. Therefore, r(θ₁) is the smallest rotation, and by composition closure r(2θ₁), r(3θ₁), …, r(kθ₁) ∀k ∈ ℤ must be in G, too. We claim that these must be all the rotations in G.

Let’s assume for the sake of contradiction, there exists θ_t which is not kθ₁ mod 2π. Then, θ_t = sθ₁ + ζ where 0 < ζ < θ₁, and r(ζ) = r(θ_t - sθ₁) = r(θ_t)r(-sθ₁) = r(θ_t)r(θ₁)^-s ⇒ r(ζ) = r(θ_t)r(θ₁)^-s, but r(θ_t)r(θ₁)^-s obviously belongs to the group of rotations ⇒ it is a rotation of an angle that belongs to {θ₁, θ₂,…, θ_l-1} with ζ < θ₁ ⊥ (by assumption, θ₁ is the minimal angle, θ₁ < θ₂ < ··· < θ_l-1).

Besides θ₁ = 2π/l. Otherwise, lθ₁ = 2π + η with η < θ₁ and r^l(θ₁) = r(2π)r(η) = r(η) with η < θ₁ ⊥ (θ₁ is the minimal angle). And therefore, we have exactly l rotations generated by r(θ₁), θ₁ = 2π/l, and ⟨r(θ₁)⟩ is the cyclic group of order l.

If ⟨r(θ₁)⟩ = G, we are done. If this is not the case, then there are reflections in G, too.

Let m be a reflection that belongs to G. If m and ⟨r(θ₁)⟩ are both in G, then by closure, m, mr, mr²,…, mr^l-1 ∈ G and all of these are distinct reflections.

1. Let’s suppose, for the sake of contradiction, that one of these elements is a rotation, mr^α = r^β ⇒ m = r^(β-α) and m would be a rotation ⊥
2. Let’s suppose, for the sake of contradiction, that there are two elements that are the same, mr^α = mr^β, α ≠ β ⇒[Cancellation laws apply] r^α = r^β, α ≠ β ⊥

Futhermore, can another reflection, say m’, be in the group?

If m’≠mr^α, then [Recall that composition of two reflections is a rotation] mm’ is a rotation in G, and since we have already shown that all rotations are in ⟨r(θ₁)⟩, mm’ = r^α ⇒ m’ = m^-1r^α = mr^α⊥. Futhermore, (mr^α)(mr^α) = [This is true for any reflection, m²=1] 1 ⇒ mr^αm = r^-α.

Therefore, we have proved that G = {1, r, r², …, r^l-1, m, mr, …, mr^l-1}, where m² = 1, r^l=1, mr^αm = r^-α. This is just the dihedral group D_p = {⟨r, m⟩| m²=1, r^l = 1, mr = r^-1m}. So we have already proved that a finite group of planar symmetries is either cyclic of some order n and isomorphic to ℤ_n or dihedral D_n.

Theorem. The finite groups of rotations in ℝ³ are ℤ_n, D_n, A₄, S₄, and A₅ up to isomorphism.

Exercise. Let’s determine the group G of rotations of the solid in the figure below, a Cuboctahedron. This is composed of six congruent squares and eight congruent equilateral triangles.  

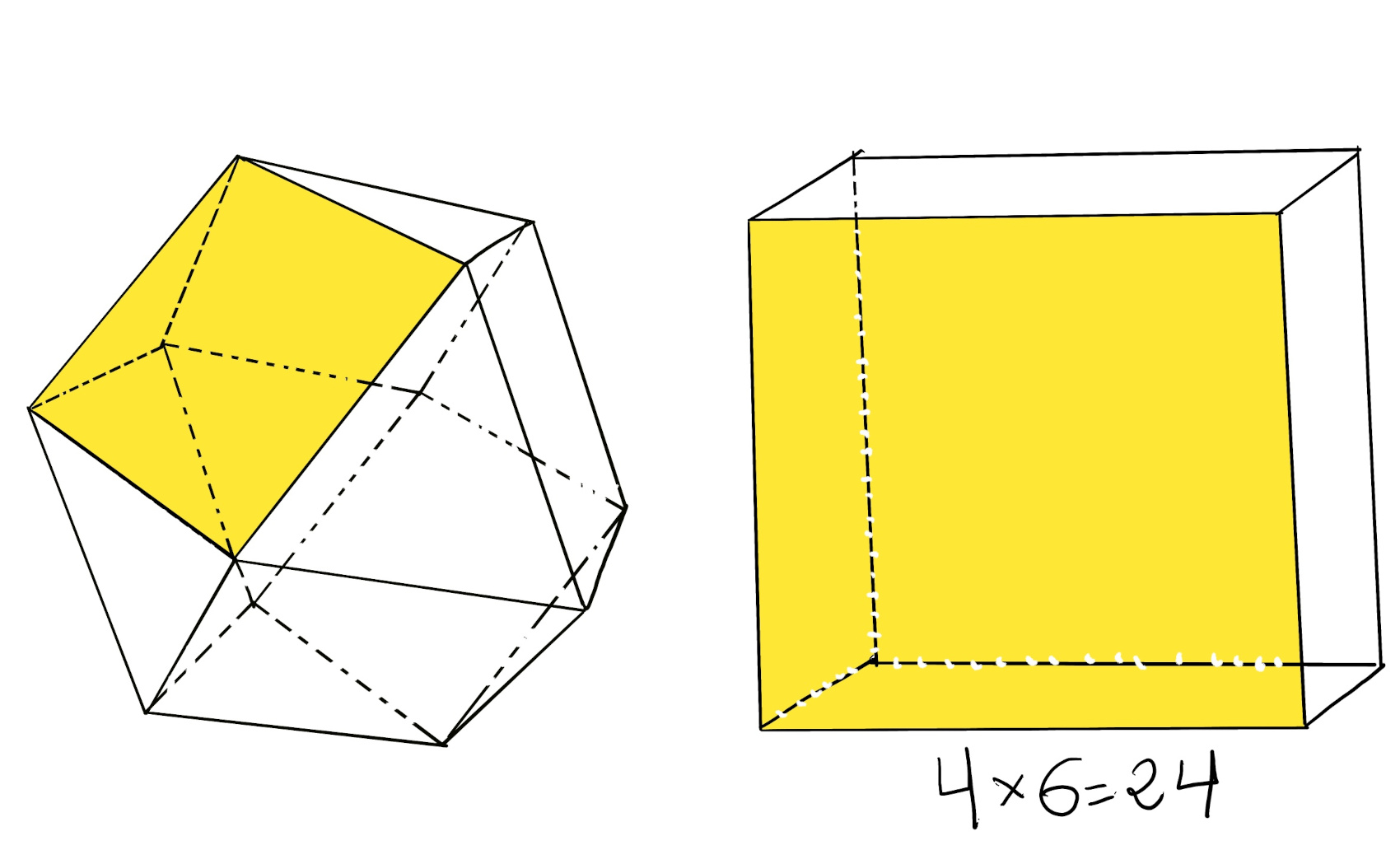
Let’s take one of the squares. There are four rotations that map this square to itself, and this square can be rotated to the location of any of the other five. So by the Orbit-Stabilizer theorem, the rotation group |G| has order |Orb(x)||Stab(x)| = 6·4 = 24 ⇒[The finite groups of rotations in ℝ³ are ℤ_n, D_n, A₄, S₄, and A₅ up to isomorphism.] G ≋ Z₂₄, D₁₂, or S₄, but Z₂₄, D₁₂ has only two elements of order 4, therefore G ≋ S₄.

Every element of the group G of rotations of the solid permutes the faces of the solid among themselves. Let G be a group action on a set X so that G x X → X. Orb(x) = {y ∈ X: ∃g ∈G: y = g * x} = is the set of faces where the chosen face can go = 6. Stab(x) = {g ∈ G: g*x = x} is the set of symmetries fixing a particular face = 4.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.