Sets. Algebra of sets

There are two ways to do great mathematics. The first is to be smarter than everybody else. The second way is to be stupider than everybody else — but persistent, Raoul Bott.

Set Theory is a branch of Maths that studies sets and their properties. What is a set? It is a well-defined collection of distinct things, elements, or objects, such as animals, utensils in the kitchen, plants, vowels (a, e, i, o, u), swearwords, followers or friends in your favorite social media, etc. The objects in these sets are called the elements of the set.

Basically, it is a list or group of unordered elements which means:

1. The order is irrelevant, {1, 2} is the same set as {2, 1}.
2. The elements in the group are not repeated or in other words, elements do not have multiplicity.

A set can be described by listing all of its elements. For example, S = {0, 2, 4, 6, 8, 10} which we read as S is the set whose elements are 0, 2, 4, 6, 8 and 10. The elements of the set are separated by commas, and they are enclosed between curly brackets. More generally, the set containing a₁, a₂, a₃, …, a_n is written as {a₁, a₂, a₃, …, a_n}.

Sets can be described by properties that the elements satisfy. If P is a property, the set is a subset of some larger set S, then the expression { x ∈ S | x satisfies P} or { x ∈ S : P(x)} denotes the set of all elements of S that satisfy P. Some examples:

• The set of odd natural numbers: { n ∈ ℕ : n = 2k + 1 for some k ∈ ℕ} = {1, 3, 5, 7, …}
• The set of even natural numbers: { n ∈ ℕ : n = 2k for some k ∈ ℕ} = {0, 2, 4, 6, …}
• The set of vowels: {a, e, i, o, u} = { x ∈ S where S is the English alphabet | x is a vowel}.
• More examples: {n ∈ ℕ : n is prime} = {2, 3, 5, 7, 11, 13, ···}, {n ∈ ℕ : 10 ≤ n ≤ 1000}, {n ∈ ℕ : n % 6 = 0}.

For a set S, we write x $\in$ S (and in latex as \in) to mean that x is an element or an object of S. We write x ∉ S to mean that x is not an element or an object of S. Two sets S and T are equal if and only if they contain or have the same elements, and in that case we can express it by writing S = T. Examples: { n ∈ ℕ : n = 2k for some k ∈ ℕ} = {0, 2, 4, 6, …}, {a, e, i, o, u} = { x ∈ S where S is the English alphabet | x is a vowel}, {0, 2, 4, 6} = {2, 4, 6, 0}, but {0, 2, 4, 6} ≠ {1, 2, 4, 6}.

The empty set is a set which has no elements. It is denoted by $\emptyset$ and written in latex as \emptyset. A set with one element is called a singleton, e.g., {a}, {2}, {John} are singletons.

A set A is a subset of another set B if all elements of A are also elements of B. It is denoted by $A \subseteq B$ (\subseteq). It is possible for A and B to be equal (A ⊆ A); if they are unequal, i.e., A ⊂ B and A ≠ B, then A is a proper subset of B. A is a proper subset of B (A ⊂ B) if there exists an element in B that does not belong to A, e.g., {0, 2, 4} ⊂ {0, 2, 4, 6}, {0, 2, 4} ⊆ {0, 2, 4}, {a, b} ⊂ {a, b, c}, ∅ ⊆ A (for any set A)

Some famous sets include:

• $\mathbb{N}$ and it is written in latex as \mathbb{N} = {n | n is a natural number} = {0, 1, 2, 3, ···}
• The set of integers and it is written in latex as \mathbb{Z}. It is denoted by the doublestruck capital letter $\mathbb{Z}$ = {…, -2, -1, 0, 1, 2, …}. It is the set of all positive whole numbers, all negative numbers, and zero.
• The set or rational numbers. It is denoted by the doublestruck capital letter ℚ. It is the set of all fractions with integer numerators and non-zero integer denominators. ℚ = {^m⁄_n: m, n ∈ ℤ, n ≠ 0}.
• The set of irrational numbers. It is any number that is not a rational number, i.e., it cannot be expressed as a fraction ratio of two integers. The following are examples of irrational numbers: $\sqrt{2}, \sqrt{3}, π$, e (Euler’s number), and φ (the golden ration)…..
• The set of rational and irrational numbers constitute the set of real numbers. It is denoted by ℝ. It includes the positive and negative integers, the fractions made from those integers (or rational numbers) and also the irrational numbers.
• Finally, the set of complex numbers are the numbers that are expressed in the form of a + ib where a and b are real numbers and ‘i’ is an imaginary number. ℂ = {a + bi : a, b ∈ R}, where i = $\sqrt{-1}$.

A bounded interval has real numbers for both endpoints. Given two real numbers a, b with a ≤ b we define four bounded intervals: (a, b) = {x ∈ ℝ : a < x < b}, [a, b] = {x ∈ ℝ : a ≤ x ≤ b}, [a, b) = {x ∈ ℝ : a ≤ x < b}, and (a, b] = {x ∈ ℝ : a < x ≤ b}; and four unbounded intervals: (a, ∞) = {x ∈ ℝ : a < x} , [a, ∞) = {x ∈ ℝ : a ≤ x} , (−∞, a) = {x ∈ ℝ : x < a} , (−∞, a] = {x ∈ ℝ : x ≤ a}. Bounded and unbounded intervals can also be closed or open intervals. Open intervals have parentheses and do not include endpoints. Closed intervals, which have brackets instead of parentheses, include endpoints.

The power set of a set S, denoted P(S), is the set of all subsets of S, e.g., power({a, b}) = {∅, {a}, {b}, {a, b}}.

Algebra of sets

The Cartesian product of two sets A and B, denoted A x B, is the set of all possible ordered pairs (a, b), where the first element of each pair, a, is an element of A, and the second, b, is an element of B. We could express this in a more mathematical or formal language as A x B = {(a, b): a ∈ A and b ∈ B}, e.g., {1, 2} x {red, yellow, blue} = {(1, red), (1, yellow), (1, blue), (2, red), (2, yellow), (2, blue)}

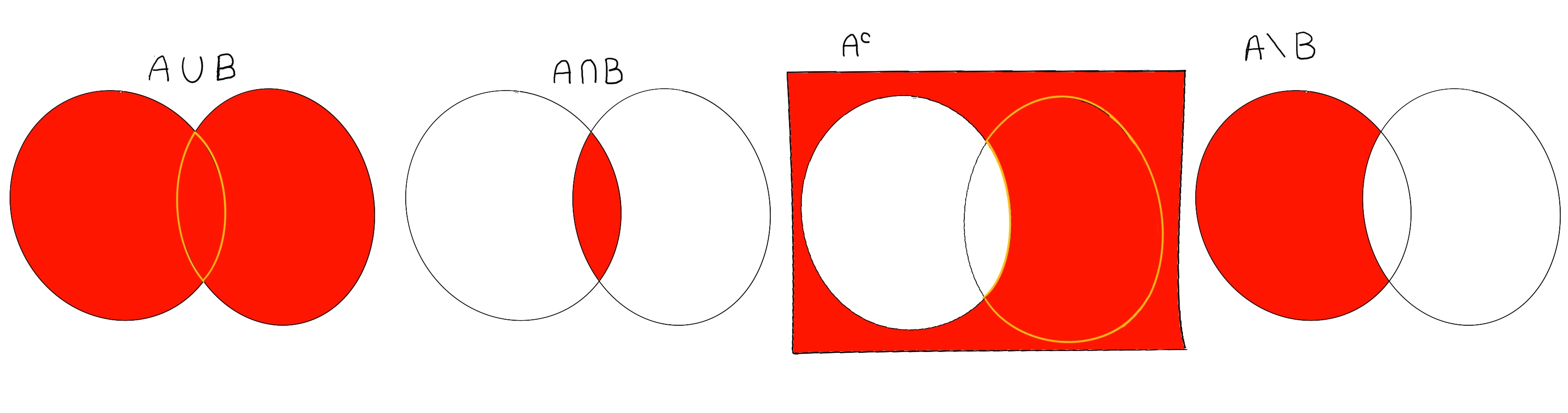
If A and B are both sets, the intersection of A and B, denoted $A \cap B$ and written in latex as A \cap B, is a new set containing all the elements that are members of both sets. Formally, A ∩ B = {x ∈ S: x ∈ A and x ∈ B}. If the intersection is empty (A ∩ B = ∅), the sets are said to be disjoint because they do not have any common members (they do not share any elements), e.g., {a, b, c, d} ∩ {c, d, e} = {c, d}, {a, b, c, d} and {red, yellow, blue} are disjoint.

The union of two sets A and B, denoted $A \cup B$ and written in latex as A \cup B, is a new set containing all the elements of A and B, and nothing else. Formally, A ∪ B = {x ∈ S: x ∈ A or x ∈ B}, e.g., {a, b, c, d} ∪ {c, d, e} = {a, b, c, d, e}, {0, 2, 4} ∪ {1, 3, 5} = {0, 1, 2, 3, 4, 5}.

By definition, A ∩ B ⊆ A, A ∩ B ⊆ B, B ⊆ A ∪ B, A ⊆ A ∪ B

For a list of set A₁, A₂, ···, A_n, then $\bigcup_{i=1}^n A_i=A_1 \bigcup A_2 \bigcup ··· \bigcup A_n$, written in latex as \bigcup_{i=1}^n A_i, $\bigcup_{i=1}^n A_i$ = {x : ∃i: 1 ≤ i ≤ n, x ∈ A_i}.

$\bigcap_{i=1}^n A_i=A_1 \bigcap A_2 \bigcap ··· \bigcap A_n$, written in latex as \bigcap_{i=1}^n A_i, $\bigcap_{i=1}^n A_i$ = {x : x ∈ A_i ∀i}.

The complement of a set A, denoted A’, A^c or $\bar A$ is the subset consisting of those elements of the universal set (say U) that are not elements of the set, that is, A^c = { x ∈ U : x ∉ A}. If U = {0, 1, 2, ··· 9}, A = {0, 2, 4, 6, 8}, then A’ = {1, 3, 5, 7, 9}. Notice that A ∩ A' = ∅, A ∪ A' = U.

The difference between two sets A and B, often denoted as $A-B$ or $A \setminus B$ and written in latex as A \setminus B, is the set containing all the elements that are in the first set, but not in the second one: A\B = {x ∈ A : x ∉ B} = A ∩ B^c, e.g., {1, 2, 5} \ {3, 5, 7} = {1, 2}, {1, 2, 5} \ {1, 2, 7} = {5}.

A Venn diagram is a widely used pictorial representation of sets and their relations. They are commonly used in school to teach basic math concepts, such as sets, unions, and intersections.

We can describe a set by associating its elements with members of an index set. We can write A = {A_i: i ∈ I} where the set I is the index set. Now, we can define unions and intersections over an index set as: ∪_i∈IA_i = { x : x ∈ A_i for some i ∈ I} = {x : ∃i ∈ I and x ∈ A_i} and ∩_i∈IA_i = { x : x ∈ A_i for all i ∈ I} = {x : ∀i ∈ I, x ∈ A_i}

Double inclusion. Let A and B be two subsets of a set S. Then A = B if and only if, aka iff, A ⊆ B and B ⊆ A.

Proof:

⇒) If A = B, then every element in A is an element of B, i.e., ∀x ∈ A, x ∈ B, so certainly A ⊆ B, and ceteris paribus (‘all else being equal’) B ⊆ A.

⇐) Let’s suppose that A ⊆ B and B ⊆ A. Then, for every element x ∈ S, if x ∈ A, then x ∈ B because by assumption A ⊆ B. Besides, for every element x ∈ S, if x ∈ B, then x ∈ A because by assumption B ⊆ A. Therefore, A = B.

Theorem. For any arbitrary sets A, B, C ⊆ U,

• Idempotency: A ∪ A = A and A ∩ A = A.
• Identity: A ∪ ∅ = A and A ∩ U = A.
• Absorption: A ∪ U = U, A ∩ ∅ = ∅, A - ∅ = A.
• Complements: A ∪ A’ = U, A ∩ A’ = ∅, A - A = ∅.
• Commutativity: A ∪ B = B ∪ A and A ∩ B = B ∩ A.
• Associativity: A ∪ (B ∪ C) = (A ∪ B) ∪ C, and A ∩ (B ∩ C) = (A ∩ B) ∩ C.
• Distributivity. (i) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C); (ii) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

Proof. (Distributivity i)

Let’s suppose that x ∈ A ∪ (B ∩ C) ⇨ x ∈ A, x ∈ (B ∩ C) or both. If x ∈ A ⇨ x ∈ (A ∪ B) and x ∈ (A ∪ C), and therefore x ∈ (A ∪ B) ∩ (A ∪ C). If x ∈ (B ∩ C), then x ∈ B and x ∈ C ⇒ x ∈ (A ∪ B) and x ∈ (A ∪ C), and therefore x ∈ (A ∪ B) ∩ (A ∪ C). So we have demonstrated that A ∪ (B ∩ C) ⊆ (A ∪ B) ∩ (A ∪ C).

Let’s suppose that x ∈ (A ∪ B) ∩ (A ∪ C), then x ∈ (A ∪ B) and x ∈ (A ∪ C). Then, if x ∈ A ⇨ x ∈ A ∪ (B ∩ C). Otherwise, if x ∉ A ⇨ x ∈ B and x ∈ C ⇨ x ∈ A ∪ (B ∩ C). So we have demonstrated that (A ∪ B) ∩ (A ∪ C) ⊆ A ∪ (B ∩ C), and by double inclusion, A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) (i).

The proof of (ii) is quite similar. May the force be with you as you try to prove it 😄.

• De Morgan’s laws. The complement of the union of two sets is the intersection of their complements and the complement of the intersection of two sets is the union of their complements. More formally, let A and B be two subsets of a bigger set S. Then, the Morgan’s laws are as follows, (A ∪ B)^c = A^c ∩ B^c, and (A ∩ B)^c = A^c ∪ B^c.

Proof. (A ∪ B)^c = A^c ∩ B^c

Suppose x ∈ (A ∪ B)^c ⇨ x is not in either A or B ⇨ x ∈ A^c and x ∈ B^c ⇨ x ∈ A^c ∩ B^c. Therefore, (A ∪ B)^c ⊆ A^c ∩ B^c

Conversely, suppose x ∈ A^c ∩ B^c ⇨ x ∈ A^c and x ∈ B^c ⇨ x ∉ A and x ∉B, so x is neither in A nor in B, and therefore x ∈ (A ∪ B)^c. Therefore, A^c ∩ B^c ⊆ (A ∪ B)^c.

(A ∪ B)^c ⊆ A^c ∩ B^c and A^c ∩ B^c ⊆ (A ∪ B)^c, and by double inclusion, (A ∪ B)^c = A^c ∩ B^c. The proof of (A ∩ B)^c = A^c ∪ B^c is quite similar and it is left to the reader.

De Morgan’s laws can be easily generalized to any number of sets. If {A_i: i ∈ I} is a family of subsets of S, then (∩_i∈IA_i)^c = ∪_i∈IA_i^c and (∪_i∈IA_i)^c = ∩_i∈IA_i^c

Truth tables. Mathematics normally uses a two-valued logic: every statement is either true or false and not both. We can use truth tables to determine how the truth or falsity of a complicated statement depends on the truth or falsity of its components. They provide another way of proving set-theoretical properties, e.g., De Morgan’s laws.

XOR (Exclusive or) is a logical operation that is true if and only if its argument differ (one is true, the other is false). NAND (not and) is described loosely as “not both” and is equivalent to the negation of the “and” operation. It produces a value of true if and only if at least one of the propositions is false. NOR (logical NOR) is the negation of the logical OR, a sentence of the form p NOR q is true when neither p nor q is true, i.e., when both p and q are false.

Cardinality. The number of distinct elements that make up or are contained in a set is called the cardinality. It is denoted by vertical bars, like absolute value signs; for instance, for a set A its cardinality is denoted by |S|, e.g., |{a, b, c}| = 3, |{a, e, i, o, u}| = 5.

More formally, the empty set ∅ is finite with |∅| = 0. A set S is finite with |S| = n + 1, if there exists s ∈ S such that |S\{s}| = n for some n ∈ N. Any set that is not finite is said to be infinite. In other words, if S = {x₁, x₂, . . . x_n}, x_i ≠ x_j ∀ i ≠ j, then |S| = n.

Let A and B be finite sets. Then, |A ∪ B| = |A| + |B| − |A ∩ B|. To say it simply, the number of elements in the union of set A and B is equal to the sum of elements of the sets A and B, minus that of their intersection, e.g., A = {a, b, c, d, e}, B = {a, e, i, o, u}, A ∩ B = {a, e}, A ∪ B = {a, b, c, d, e, i, o, u}, and |A ∪ B| = |A| + |B| − |A ∩ B| = 5 + 5 - 2 = 8.

Proof.

The sum | A | + | B | includes all the elements of A ∪ B, but, and this is the key🔑 point, its counts the elements of A ∩ B twice ⇒ | A | + | B | = | A ∪ B | - | A ∩ B | ⇒ |A ∪ B| = |A| + |B| − |A ∩ B| ∎

If a set A is a finite set with |A| = n, then its power set has |P(A)| = 2ⁿ.

Proof.

• If |A| = 0 ⇨ A = ∅, so it is the empty set with no elements, and a single subset, ∅, and therefore |P(A)| = 2ⁿ = 2⁰ = 1.
• Let’s suppose that n ≥ 0 and that |P(S)| = 2ⁿ ∀S: |S| = n. Let A be any set with |A| = n + 1, so there is an element “a” and a set A’ = A\a with |A’| = n. Any subset of A must either contain “a” or not, so P(A) = P(A’) ∪ {S ∪ {a} : S ∈ P(A’)}.

These two subsets are obviously disjoint, and therefore (If A, B are disjoint, |A ∪ B| = |A| + |B|):

|P(A)| = |P(A’)| + |{S ∪ {a} : S ∈ P(A’)}| = 2ⁿ + 2ⁿ [These two sets has the same cardinality and by our induction hypothesis, |P(A’)| = 2ⁿ] = 2ⁿ⁺¹∎