Roots of Unity.

“I refuse to answer without my lawyer or even worse, without knowing the answer”, Apocalypse, Anawim, #justtothepoint.

Complex Numbers

A complex number is a number z that can be expressed or written in the form a + bi, where a and b are real numbers, and i is the imaginary unit defined by i² = −1 or i = $\sqrt{-1}$. The real numbers a and b are called the real and imaginary part of z respectively.

Operations

x = 8 + 5i, y = 7 - 2i; Let’s perform all the standard operations with complex numbers:

• When adding or subtracting numbers, follow the simple rule of combining like-terms, that is, combine the real parts together, then combine the imaginary parts together. x + y = (a + bi) + (c + di) = (a + c) + (b + d)i = 15 + 3i.

• x - y = (a + bi) - (c + di) = (a - c) + (b - d)i = 1 + 7i.

• x * y = (a + bi) * (c + di) = (ac−bd) + (ad+bc)i = 66 + 19i.

• x / y = (a + bi) / (c + di) = $\frac{(a+bi)}{(c + di)}\frac{c-di}{c-di}=\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i=\frac{46}{53}+\frac{51}{53}i$ ≈ 0.86792 + 0.96226i.

  To divide complex numbers, we multiply the numerator and the denominator by the complex conjugate of the denominator, that is, $\overline {c + di}=c - di$. Notice that $z\bar z=(a+bi)(a-bi)=a^2-abi+abi+b^2=a^2+b^2$

• Powers of i: i² = -1, i³ = i²i = -i, i⁴ = 1, iⁿ = i^{n (mod 4)}, e.g., i¹⁷ = i¹ = 1, i²⁴ = i⁰ = 1, i²⁶ = i² = -1

  This property of powers of i is explained in group theory by considering that H = {1, -1, i, -i} ≤ ℂ^* is a cyclic subgroup of ℂ^* of order 4.

Definition. Let ζ ∈ ℂ^* and n be a positive integer. We say that ζ is an nth root of unity if ζⁿ = 1. Futhermore, ζ is said to be a primitive nth root of unity if n is the smallest positive integer such that ζⁿ = 1., that is, a primitive nth root of unity is an nth root of unity that is also not an mth root of unity for any m < n.

• {1} is the set of first roots of unity, 1 is the primitive first root of unity.
• {1, -1} is the set of square roots (2nd roots) of unity, -1 is the primitive square root of unity.
• {1,w = $e^{\frac{2π}{3}}i$, w² = $e^{\frac{4π}{3}}i$} is the set of 3rd (cube) roots of unity. The primitive cube roots of unity in ℂ are w, w².
• {1, -1, i, -i} is the set of 4th roots of unity. i and -i are the two primitives 4th roots of unity.
• {1, $e^{\frac{2π}{5}}i, e^{\frac{4π}{5}}i, e^{\frac{6π}{5}}i, e^{\frac{8π}{5}}i$} is the set of 5th roots of unity. The primitive 5th roots of unity in ℂ are $e^{\frac{2π}{5}}i, e^{\frac{4π}{5}}i, e^{\frac{6π}{5}}i, e^{\frac{8π}{5}}i$.

A complex number z = x + iy can be identified with an order pair (x, y) of real numbers, which in turn may be interpreted as coordinates of a point in a two-dimensional space. It suggests the use of Cartesian coordinates in the complex plane. The horizontal axis is used to display the real part and becomes the real axis, and the vertical axis is used to display the imaginary part and becomes the imaginary axis (Figure 1.a)  

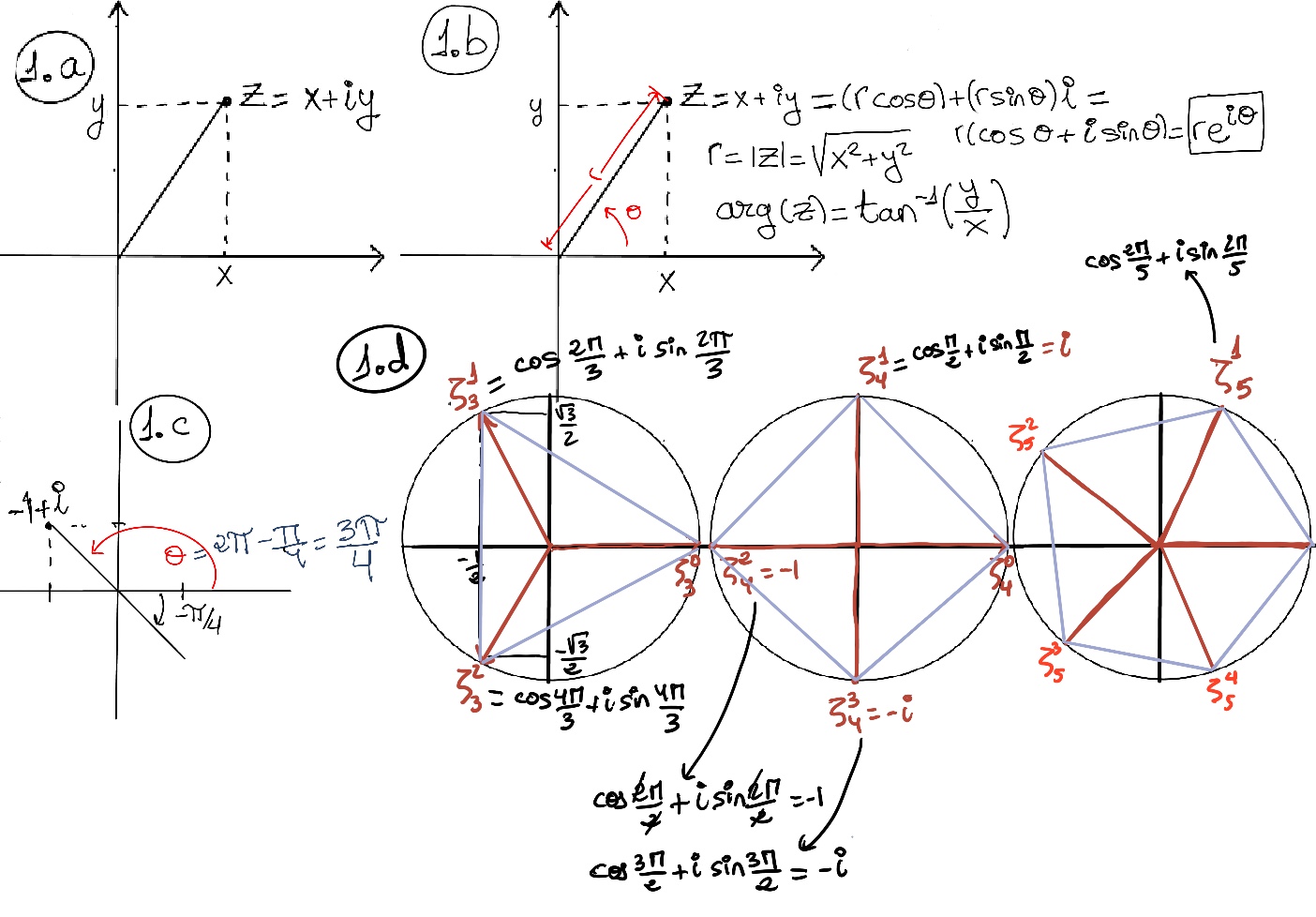
An alternative option is the polar coordinate system that uses the distance of the point z from the origin (radius) and the angle between the positive real axis and the line segment Oz in a counterclockwise sense (the angle θ is called the argument, arg(z)). Thus, a complex number is defined by (Figure 1.b.),

• Its radius, absolute value, or modulus, denoted as r = |z| = |x + iy| = $\sqrt{x^2+y^2}$
• The angle θ between the positive real axis and the line segment Oz. It is called its argument. θ = arg(z) = $tan^{-1}(\frac{y}{x})=sin^{-1}(\frac{y}{|z|})=cos^{-1}(\frac{x}{|z|})$

  Notice that x = rcosθ, y = rsinθ where r and θ are the magnitude and argument of z respectively.

Therefore, ∀z ∈ ℂ, z = x + yi, r = |z|, θ = arg(z), then z = x + yi = (rcosθ) + (rsinθ)i = r(cosθ + isinθ)

Example. Let z = -1 + i. r = |z| = $\sqrt{(-1)^2+1^2}=\sqrt{2}$, θ = arg(z) = $tan^{-1}(\frac{1}{-1})=tan^{-1}(-1)=-\frac{π}{4}+2π$ (It is in the second quadrant, see Figure 1.c) = $\frac{3π}{4}$ (135°). z = $\sqrt{2}(cos(\frac{3π}{4})+isin(\frac{3π}{4}))$.  

If we want to compute exponents, we should consider that a^z = a^{x +iy} = a^xa^yi = a^x(a^yi).

a^iy = $(e^{lna})^{iy}=e^{iylna}=(e^{iy})^{lna}$

Euler’s Formula. Let z = x + yi, r = |z|, and θ = arg(z). Then, z = r(cosθ + isinθ) = re^iθ. In particular, e^iθ = cosθ + isinθ.

Proof.

Recall. The Taylor series of a real or complex-valued function that is infinitely differentiable at a real or complex number a, is the power series $f(a)+\frac{f’(a)}{1!}(x-a)+\frac{f’’(a)}{2!}(x-a)^2+···+\frac{f^n(a)}{n!}(x-a)^n+···$. It is a power series that approximates the function f near x = a.

We are going to use the Taylor series of e^x which can be extended to any complex number,

e^z =[$\frac{f^n(a)}{n!}(x-a)^n = \frac{e^0}{n!}x^n$] = $\sum_{n=0}^\infty \frac{z^n}{n!}=1+z+\frac{z^2}{2!}+\frac{z^3}{3!}+\frac{z^4}{4!}+…$

sin(z) = $\sum_{n=0}^\infty (-1)^n\frac{z^{2n+1}}{(2n+1)!}=z-\frac{z^3}{3!}+\frac{z^5}{5!}-\frac{z^7}{7!}+…$

cos(z) = $\sum_{n=0}^\infty (-1)^n\frac{z^{2n}}{(2n)!}=1-\frac{z^2}{2!}+\frac{z^4}{4!}-\frac{z^6}{6!}+…$

Therefore,

e^iθ = $\sum_{n=0}^\infty \frac{(iθ)^n}{n!}=1+(iθ)+\frac{(iθ)^2}{2!}+\frac{(iθ)^3}{3!}+\frac{(iθ)^4}{4!}+…=1+(iθ)-\frac{θ^2}{2!}-\frac{iθ^3}{3!}+\frac{θ^4}{4!}+\frac{iθ^5}{5!}-\frac{θ^6}{6!}-\frac{iθ^7}{7!}+…=(1-\frac{θ^2}{2!}+\frac{θ^4}{4!}-\frac{θ^6}{6!}+…)+(iθ-\frac{iθ^3}{3!}+\frac{iθ^5}{5!}-\frac{iθ^7}{7!}+…)=(1-\frac{θ^2}{2!}+\frac{θ^4}{4!}-\frac{θ^6}{6!}+…)+i(θ-\frac{θ^3}{3!}+\frac{θ^5}{5!}-\frac{θ^7}{7!}+…)=\sum_{n=0}^\infty (-1)^n\frac{θ^{2n}}{(2n)!}+i(\sum_{n=0}^\infty (-1)^n\frac{θ^{2n+1}}{(2n+1)!})$ = cos(θ) + isin(θ).

Finally, z = r(cos(θ)+isin(θ)) = re^iθ ∎

Examples:

• eⁱ⁰ = 1, e^iπ/2 = πi, e^iπ = cosπ + isinπ = -1, e^3πi/2 = cos(3π/2) + isin(3π/2) = -i.
• $e^{\frac{iπ}{4}}=cos\frac{π}{4}+isin\frac{π}{4}=\frac{1}{\sqrt{2}}+i\frac{1}{\sqrt{2}}$
• $3e^{\frac{iπ}{6}}=3(cos\frac{π}{6}+isin\frac{π}{6})= 3(0.8660 + i0.5)= 2.60 + 1.50i$

Corollary. Let z, w be complex numbers, z, w ∈ ℂ, z = r(cosθ + isinθ) and w = s(cosφ +isenφ). Then, zw = rs(cos(θ + φ) + isin(θ + φ)) and in particular, |zw| = |z|·|w|.

Proof.

zw = $re^{iθ}se^{iφ}=rse^{iθ+iφ}=rse^{(θ+φ)i}=$ rs(cos(θ + φ) + isin(θ + φ))∎

Corollary. Let $ξ_n=e^{\frac{2πi}{n}} = cos(\frac{2π}{n})+isin(\frac{2π}{n})$. Then, ξ_n is a primitive nth root of unity and ξ_n^k is a primitive root of unity for each integer k coprime to n.

Proof.

By De Moivre’s formula: (cosx + isinx)ⁿ = cosnx + isinnx ⇒ [Taking x = ^2π⁄_n] $(cos\frac{2π}{n}+isin\frac{2π}{n})^n=cos2π+isin2π=1$ but $(cos\frac{2π}{n}+isin\frac{2π}{n})^k=cos\frac{2kπ}{n}+isin\frac{2kπ}{n}≠1$ for k = 1, 2, …, n-1. In other words, $e^{\frac{2πi}{n}}=(cos\frac{2π}{n}+isin\frac{2π}{n})$ is a primitive nth root of unity.

Theorem. Let Z_n denote the set of all nth roots of unity in ℂ^*. Then Z_n is a cyclic subgroup of ℂ^*. This subgroup is generated by any primitive nth root of unity.

Proof.

Let ζ ∈ ℂ^* be a primitive nth root of unity and let us consider the cyclic subgroup generated by it, that is, G = ⟨ζ⟩.

We claim that any power of ζ is an nth root of unity since: (ζ^m)ⁿ = [By exponent rules] (ζⁿ)^m = [ζ is an nth root of unity] 1^m = 1. Therefore, G = ⟨ζ⟩ ⊆ Z_n

ζ is a primitive nth root of unity, so its order is n, |ζ| = n, and therefore the cyclic subgroup generated by it has order n, too, |G| = |⟨ζ⟩| = n.

Z_n denotes the set of all nth roots of unity in ℂ^*, that is the set of the roots of the polynomial Xⁿ - 1. By the fundamental theorem of algebra, we know that Xⁿ -1 has exactly n complex roots, and therefore n = |G| = ⟨ζ⟩ ≤ |Z_n| ≤ n ⇒ |G| = ⟨ζ⟩ = Z_n = n ∎

The generators of a cyclic group are those elements whose order is equal to the order of the group, that is, those elements whose multiplicative order is n, and that is precisely what primitive roots are (n is the smallest positive integer such that ζⁿ=1).

Definition. The circle group, denoted by $\mathbb {S}^1$, is the multiplicative group of all complex numbers with absolute value 1, that is, the unit circle in the complex plane. $\mathbb {S}^1$ = {z ∈ ℂ^*: |z| = 1}

Theorem. $\mathbb {S}^1$ ≤ ℂ^* which contains Z_n for each n.

Proof.

First, let’s prove $\mathbb {S}^1$ is a group.

1. ∀μ, v ∈ $\mathbb {S}^1$, |μv| = |μ||v| = 1·1 = 1 ⇒ μv ∈ $\mathbb {S}^1$
2. |1| = 1 ⇒ 1 ∈ $\mathbb {S}^1$
3. ∀μ ∈ $\mathbb {S}^1$, |μ^-1| = |μ^-1|·1 =[Since μ ∈ $\mathbb {S}^1$ ⇒ |μ| = 1] |μ^-1|·|μ| = |μ^-1μ| =[Obviously, μ^-1·μ = 1] |1| = 1 ⇒ μ^-1 ∈ $\mathbb {S}^1$ ⇒ $\mathbb {S}^1$ ≤ ℂ^*

Let ζ = $e^{\frac{2πi}{n}}$ be a primitive nth root of unity, Z_n = ⟨ζ⟩ ⇒ |ζ| = cos²(^2π⁄_n) + sin²(^2π⁄_n) = 1 ⇒ Z_n ⊆ $\mathbb {S}^1$ for each n. In the complex plane the nth roots of unity are at the vertices of a regular n-sided polygon inscribed in the unit circle, with one vertex at 1, (Figure 1.d)

Remember that $(cos\frac{2π}{n}+isin\frac{2π}{n})^n=cos2π+isin2π=1$ but $(cos\frac{2π}{n}+isin\frac{2π}{n})^k=cos\frac{2kπ}{n}+isin\frac{2kπ}{n}≠1$ for k = 1, 2, …, n-1.  

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.