Partially Ordered Sets. Hasse Diagrams.

“Mr. Smith, could you explain to us what recursion is all about?” The professor in Introduction to Programming asked an apathetic student. “I don’t know the question, but sex, money, or both is definitely the answer, and God, justice, our values, and love are just the excuses,” I replied. “You shall not pass,” the teacher was far from amused, Apocalypse, Anawim, #justtothepoint.

Definition. A partial order $\preceq$ on a set X (written in LaTeX as \preceq) is a binary relation $\preceq$ ⊆ X × X or a subset of the Cartesian product such that is reflexive, antisymmetric, and transitive, ∀x, y, z∈ X

1. Reflexive: x $\preceq$ x.
2. Antisymmetric: if x $\preceq$ y and y $\preceq$ x ⇒ x = y.
3. Transitive: If x $\preceq$ y and y $\preceq$ z, then x $\preceq$ z.

A partially ordered set or poset for short is a set endowed or equipped with a partial order. A set is partially ordered if there is some relation $\preceq$ on the set such that either x $\preceq$ y, y $\preceq$ x, that is, x and y are comparable or x and y are unrelated, e.g., “is father of” and the lexicographical order, that is, (a, b) $\preceq$ (c, d) if a < c or (a = c and b $\preceq$ d).

Examples

• ∀a, b ∈ ℝ (or ℚ, ℤ, ℕ) a ≤ b if b -a is non-negative, that is, the usual ordering of ℝ, is a partial ordering.
• Let X be any set, P(X) denotes the power set of X, which is the set of all subsets of the set X including the set itself and the empty set ∅. (P(X), ⊆) is a partially ordered set. Let A, B, C ∈ P(X), A, B, C ⊆ X

1. Reflexive. If x ∈ A ⇒ x ∈ A ⇒ A ⊆ A 😄
2. Antisymmetric. A ⊆ B and B ⊆ A ⇒ B = A.
3. Transitive. A ⊆ B and B ⊆ C ⇒ ∀x ∈ A ⇒[A ⊆ B] x ∈ B ⇒[B ⊆ C] ⇒ x ∈ C, therefore A ⊆ C.

The word partial is used to indicate that not every pair of elements needs to be comparable, e.g., let X = {a, b, c, d}, A = {a, b}, B = {c, d}, A ⊈ B and B ⊈ A. A and B are not comparable.

• Let G be a group. Then, the set of all subgroups of G forms a partially ordered set under ≤.
• The set of ℕ natural numbers equipped with the relation of divisibility (m | n ↭ ∃k ∈ ℕ: n = km) is a partially ordered set, e.g., 1 | 2 or 1 | 3, 2 | 4, but 2 ɫ 3.
• Suppose S is a set, (T, ≤_T) is a partially ordered set, and let $\mathbb{F}$ denote the set of functions f: S → T. The relation ≤ on $\mathbb{F}$ defined by f ≤ g ↭ f(x) ≤_T g(x) ∀x ∈ S is a partial order on $\mathbb{F}$.

Hasse diagram

A Hasse or lattice diagram is a type of mathematical diagram used to represent a finite partially ordered set (X, $\preceq$). It is a graph whose vertices are the elements of X and for which an edge or segment between two vertices (x, y) exists if they are comparable, x $\preceq$ y and there's no intermediate element that sit between them, that is, whenever x $\preceq$ z $\preceq$ y either z = x or z = y.

Examples:

• Let X = {a, b, c}, (P(X), ⊆) is a partially ordered set. |P(X)| = 2³ = 8.

  Because of the transitivity property, any path upward the graph shows comparability of subsets.

We are showing the Hasse diagrams for X = {a, b}, (P(X), ⊆) -Figure 1.a.-, and X = {a, b, c}, (P(X), ⊆) -Figure 1.b.-. Notice ∅ ⊆ {a} ⊆ {a, b} ⊆ X  

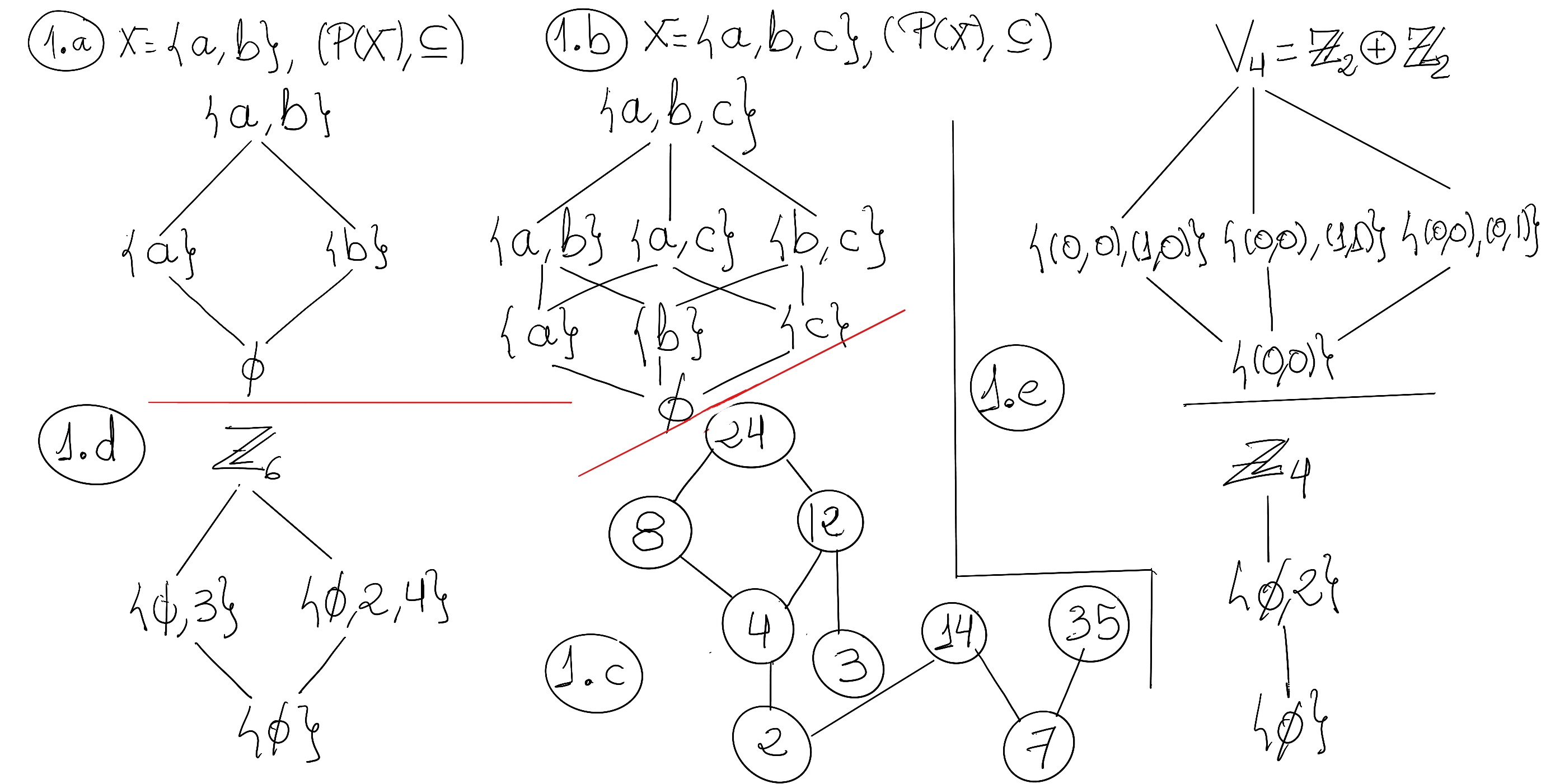
• Figure 1.c. shows the Hasse diagram for A = {2, 3, 4, 7, 8, 12, 14, 24, 35}, and R the divides relation on A = {(x, y) ∈ A x A: x | y}

• The Hasse diagram for the subgroups of ℤ₆ is shown in Figure 1.d  

• ℤ₂⊕ℤ₂ = {(0, 0), (1, 0), (0, 1), (1, 1)}. |ℤ₂ ⊕ ℤ₂| = 4 = 2p, p=2, 2 prime, and it is not cyclic ⇒ [Classification of Groups of Order 2p] G is either isomorphic to ℤ₄ (cyclic ⊥) or the dihedral group D₂. Therefore, ℤ₂ ⊕ ℤ₂ ≋ D₂ ≋ K₄, the Klein-four-group. Its Hasse diagrams is shown in Figure 1.e.

Besides, the group ℤ₄ = ⟨1⟩ = {0, 1, 2, 3} is a cyclic group of order 4 with a completely different Hasse diagram. It has only one proper subgroup, namely {0, 2} = ⟨2⟩.  

• A square is a regular quadrilateral (four-sided polygon), which means that it has four equal sides and four equal right angles (90° angles, π/2 radian angles).

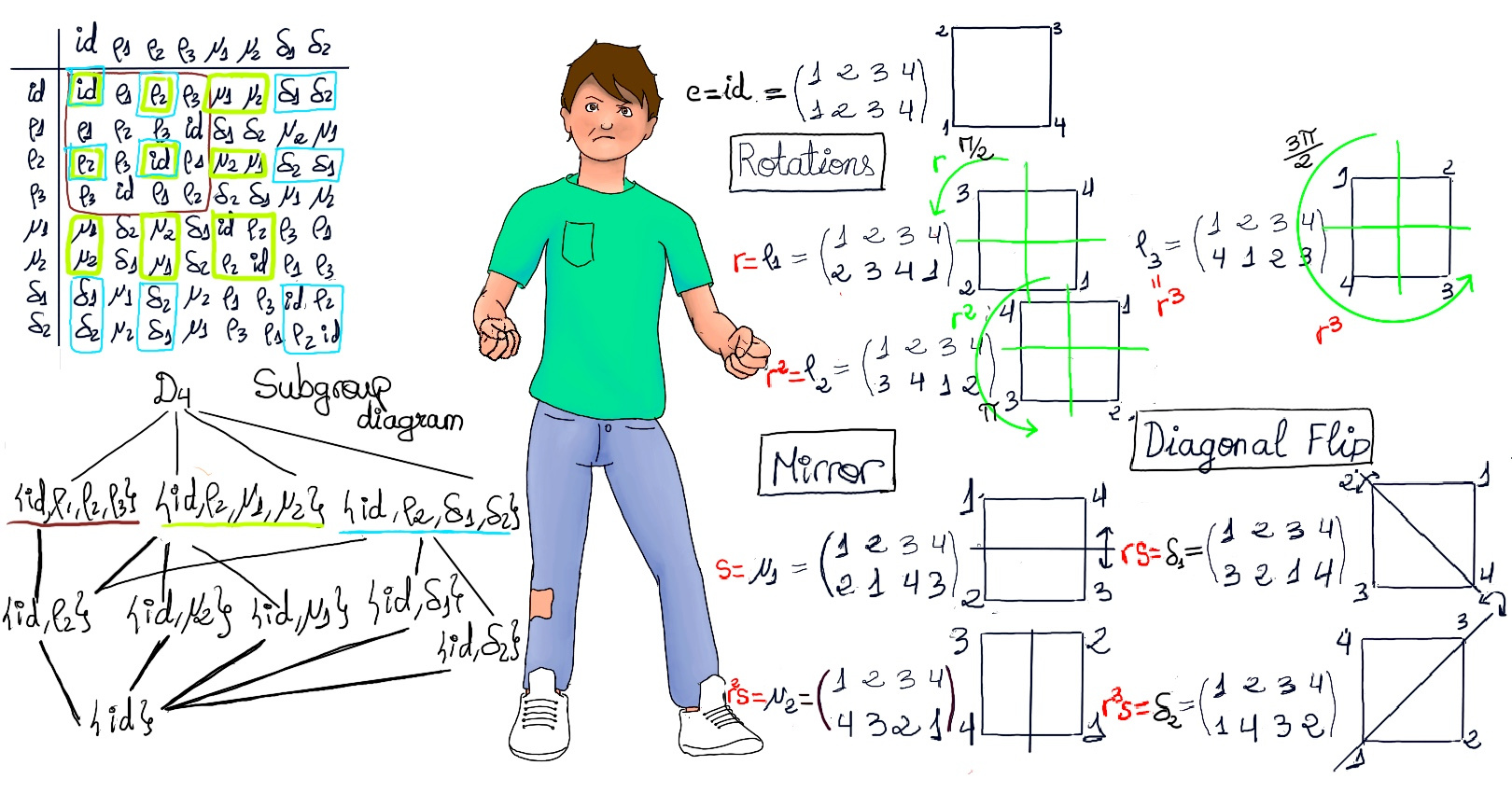
The dihedral group D4 is the symmetry group of the square. D₄ = {id (e), rotations (ρ₁ -90° around the center anticlockwise-, ρ₂ -180°-, and ρ₃ -270°-), reflections or mirror images in the x -horizontal- and y -diagonal- axes (μ₁, μ₂), and reflections in the diagonals δ₁ and δ₂ respectively} = {e, r, r², r³, s, rs, r²s, r³s} = ⟨r, s | r⁴ = s² = e, rs = sr³⟩.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.