Rolle's and the Mean Value Theorems

Success is not final, failure is not fatal: It is the courage to continue that counts, Winston Churchill.

Recall

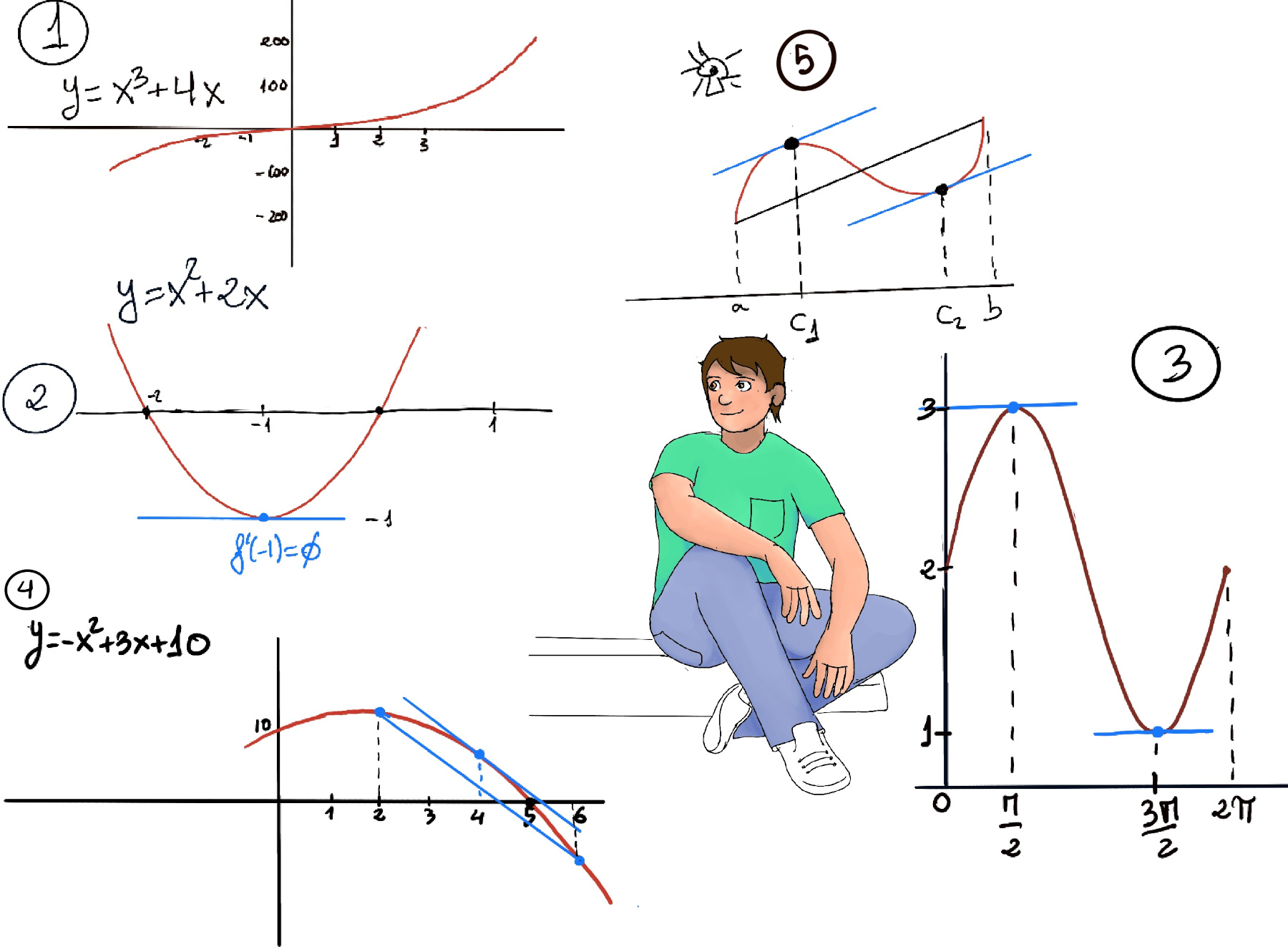
Extreme Value Theorem. If f is a continuous function on an interval [a,b], then f has both a maximum and minimum values on [a,b]. It states that if a function is continuous on a closed interval, then the function must have a maximum and a minimum on the interval (Figure 1.f.)  

Fermat’s Theorem. If a function ƒ(x) is defined on the interval (a, b), it has a local extremum (relative extrema) on the interval at x = c, and ƒ′(c) exists, then x = c is a critical point of f(x) and f'(c) = 0 (Figure 1.a.)

Rolle’s Theorem

Rolle’s Theorem. It states that any real-valued differentiable function that has equal values at two distinct points must have at least one stationary point somewhere between them, that is, a point where the first derivative is zero. If a real-valued function f is continuous on a proper closed interval [a, b], differentiable on the open interval (a, b), and f (a) = f (b), then there exists at least one c in the open interval (a, b) such that f'(c) = 0 (Figure 1.c, 1.d).  

Proof. There are two cases.

• f(x) = k, ∀x in [a, b] where k is a constant. ⇒ f’(x) = 0 ∀x in [a, b], and we can take c to be any number in the interval.
• Since f is continuous on [a, b] by the Extreme Value Theorem we know that the function must have a maximum M and a minimum on the interval m.

M ≠ m. Otherwise, if M = m, then f is constant ∀x in [a, b] ⇒ f’(x) = 0 ∀x in [a, b], and we can take c to be any number in the interval (a, b).

If M ≠ m. If f(a)=M, then f(b) = f(a) = M ⇒ m have to occur in the open interval (a, b). Therefore, there is at least one maximum or minimum in the open interval (a, b).

Without lose of generosity, let’s assume that f has a maximum in the open interval (a, b), that is, f has a maximum at some c in (a, b) ⇒ [By Fermat’s Theorem, f has a maximum at c ∈ (a, b) and f is differentiable on the open interval (a, b), so f’(c) exists] f’(c) = 0 ∎

Mean Value Theorem

The mean value theorem states that if f is a continuous function on the closed interval [a,b] and differentiable on the open interval (a, b), then there exists a number c ∈ (a,b) such that the tangent at c is parallel to the secant line through the endpoints, that is, $f’(c) = \frac{f(b)-f(a)}{b-a}$. Figure 1.e. and 5 (at least a number c ∈ (a,b), it may have two or more c₁ and c₂).

In other words, there exist a point c within that open interval where the instantaneous rate of change equals the average rate of change over the interval.

Geometrically, it states that the slope of the secant line through the end points is the same as the slope of the tangent line at x = c. Physically, there is a point at which the average velocity is equal to instantaneous velocity.  

Proof.

We will use Rolle’s Theorem. If a real-valued function f is continuous on a proper closed interval [a, b], differentiable on the open interval (a, b), and f (a) = f (b), then there exists at least one c in the open interval (a, b) such that f'(c) = 0.

Let $g(x) = f(x) - \frac{f(b)-f(a)}{b-a}x$

$g(a) = f(a) - \frac{f(b)-f(a)}{b-a}a = f(a)(1+\frac{a}{b-a})- a\frac{f(b)}{b-a} = f(a)\frac{b}{b-a}- f(b)\frac{a}{b-a}$

$g(b) = f(b) - \frac{f(b)-f(a)}{b-a}b = f(b)(1-\frac{b}{b-a})+ b\frac{f(a)}{b-a} = f(b)\frac{-a}{b-a}+ f(a)\frac{b}{b-a} = g(a)$

Therefore, ∃c ε (a, b): g’(c) = 0

$g’(c) = 0 = f’(c) - \frac{f(b)-f(a)}{b-a} ⇒∃c ε (a, b): f’(c) = \frac{f(b)-f(a)}{b-a}$∎

Solved examples

• Let f(x) = x² + 2x over [-2, 0], f(-2) = 0 = f(0). Since f is a polynomial, it is both continuous and differentiable everywhere.

Figure 2. By Roller’s theorem, ∃c ∈ (-2, 0) such that f’(c) = 0.  

f’(x) = 2x + 2 ⇒ 2c +2 = 0 ⇒ 2(c + 1) = 0 ⇒ c = -1. Therefore, x = -1 is the point where the slope of the secant line through the end points 0 and 2 is the same as the slope of the tangent line at x = -1 (f’(-1) = 0).

• Let f(x) = sin(x) + 2 over [0, 2π)], f(0) = f(2π) = 2, f is both continuous and differentiable everywhere.

Figure 3. By Roller’s theorem, ∃c ∈ (0, 2π), there may be more than one, such that f’(c) = 0.

f’(x) = cos(x) ⇒ ∃c ∈ (0, 2π): cos(c) = 0 ⇒ $c = \frac{π}{2}, c = \frac{3π}{2}$.

• Let f(x) = $\frac{1}{x^2}$ over [-1, 1], f(-1) = f(1) = 1, but since f is undefined at x = 0, it does not satisfy all conditions of Rolle’s theorem.

• Let f(x) = x³ +4x over [-1, 1], f(-1) = -5, f(1) = 5. Since f is a polynomial, it is both continuous and differentiable everywhere.

Figure 1. By the MVT, ∃c ∈ (-1, 1): f’(c) = $\frac{5-(-5)}{1-(-1)} = \frac{10}{2} = 5.$

f’(x) = 3x² +4 ⇒ $5 = 3·c^2 +4 ⇒ c = ±\sqrt[3]{\frac{1}{3}} = ±\frac{1}{\sqrt{3}} = ±\frac{\sqrt{3}}{3}≈ ± 0.58$. The vertical scale is so large that the “interesting” part of the graph looks like it is almost all zero.

• Let f(x) = |x| - 1 over [-1, 1], f is continuous over [-1, 1] but f is not differentiable at x = 0, f(-1) = f(1) = 0, but f’(c) ≠ 0( = (0-0)/2 ) ∀c ∈ (-1, 1).

If f is not differentiable, even at a single point, the result may not holdbecause it does not satisfy all conditions of Rolle’s theorem.

• Let f(x) = -x²+3x +10 over the interval [2, 6]. What is the average rate of change? When does the instantaneous rate of change equal the average rate of change?

Figure 4. The average rate of change = $\frac{f(6)-f(2)}{6-2} = \frac{(-36+18+10)-(-4+6+10)}{4} = \frac{-20}{4} = 5.$

Since f is a polynomial, it is both continuous and differentiable everywhere. By the Mean Value Theorem, ∃c ∈ (2, 6): f’(c) = -2c +3 = -5, c = 4 is the point at which the instantaneous rate of change equals the average rate of change.

• A hot air balloon is launched into the air with a human pilot. The twice-differentiable function f models the balloon’s height, measured in meters, at time t, measured in minutes. The table gives values of the f(t) of the ballon at selected times t. For 20 ≤ t ≤ 30, there must be a time when the balloon’s velocity is 1.5 meters per minute.

The average ballon velocity (20, 30) = $\frac{f(30)-f(20)}{30-20} = \frac{80-65}{10} = 1.5$ meters/minutes ⇒ Since f is twice-differentiable, according to the Mean Value Theorem, there must be at least a value c ∈ (20, 30) where f’(c), that is, the ballon’s (instant) velocity is 1.5.

Increasing and decreasing functions.

Let’s suppose f is continuous on the interval [a, b], and diferenciable on (a, b).

1. If f'(x) > 0 ∀x ∈ (a, b), then f is increasing on (a, b).
2. If f'(x) < 0 ∀x ∈ (a, b), then f is decreasing on (a, b).
3. If f'(x) = 0 ∀x ∈ (a, b), then f is constant on (a, b).

Proof: ∀ x₁, x₂ ∈ (a, b), x₁ < x₂, then $x_2-x_1>0$ and the Mean Value Theorem guarantees that we can find a c ∈ (x₁, x₂): $\frac{f(x_2)-f(x_1)}{x_2-x_1}=f’(c)$ ⇒ $f(x_2)=f(x_1)+f’(c)(x_2-x_1)$

1. If f’(x) > 0 ∀x ∈ (a, b) ⇒ f’(c) > 0 ⇒ f(x₂) > f(x₁) ⇒ f is increasing.
2. If f’(x) < 0 ∀x ∈ (a, b) ⇒ f’(c) < 0 ⇒ f(x₂) < f(x₁) ⇒ f is decreasing.
3. If f’(x) = 0 ∀x ∈ (a, b) ⇒ f’(c) = 0 ⇒ f(x₂) = f(x₁) ⇒ f is constant.

Solved exercises

• Show that the function f: ℝ → ℝ defined by f(x) = x³ -3x² +3x +5 is increasing on ℝ.

Since x³ -3x² +3x +5 is a polynomial ⇒ f is continuous and differentiable on ℝ. f’(x) = 3x² -6x +3 = 3(x -1)² ≥ 0 ∀x ∈ℝ ⇒ f is increasing on ℝ.

• Find the intervals in which the function f: ℝ → ℝ defined by f(x) = 2x³ -15x² + 36x +5 is increasing or decreasing.

Since 2x³ -15x² + 36x +5 is a polynomial ⇒ f is continuous and differentiable on ℝ. f’(x) = 6x² -30x +36 = 6(x -2)(x -3).

1. x < 2, f’(x) > 0 ⇒ f is increasing (-∞, 2).
2. 2 < x < 3, f’(x) < 0 ⇒ f is decreasing (2, 3).
3. x > 3, f’(x) > 0 ⇒ f is increasing (3, ∞).

• e^x > x + 1 ∀x >0.

Let be f(x) = e^x -x -1, f is continuous and differentiable on (0, ∞), f(0) = 0, f’(x) = e^x-1 > 0 ∀x >0 (Recall, e^x is monotonically increasing, e⁰ = 1) ⇒ f is increasing ∀x >0 ⇒ f(x) > 0 ∀x >0 ⇒ e^x -x -1 > 0 ⇒ e^x > x + 1 ∀x >0

• e^x > x + 1 + $\frac{x^{2}}{2},$ ∀x >0.

Similarly, let be g(x) = e^x -x -1 -$\frac{x^{2}}{2}$, g(0) = 0, g’(x) = e^x -1 -x > 0 ∀x >0 (previous example) ⇒ g is increasing ⇒ g(x) > 0 ∀x >0 ⇒ e^x > x + 1 + $\frac{x^{2}}{2}, $∀x >0

Futhermore, e^x > x + 1 + $\frac{x^{2}}{2} + \frac{x^{3}}{3.2} + …$ (it is left for the reader as an exercise), but in the infinite they are both equal.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus. College Algebra and Abstract Algebra.
8. MIT OpenCourseWare 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007.
9. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.