Limits

To be a star, you must shine your own light, follow your path, and don’t worry about the darkness, for that is when the stars shine brightest. Always do what you are afraid to do, Ralph Waldo.

Recall

Definition. A function f is a rule, relationship, or correspondence that assigns to each element of one set (x ∈ D), called the domain, exactly one element of a second set, called the range (y ∈ E).

The pair (x, y) is denoted as y = f(x). Typically, the sets D and E will be both the set of real numbers, ℝ. A mathematical function is like a black box that takes certain input values and generates corresponding output values (Figure E).

Intuitive definition

Very loosing speaking, a limit is the value to which a function grows close as the input get closer and closer to some other given value.

A limit involves what is going on around a given point, say “a”. It is the value that a function approaches as its input approaches that point “a” but does not care what the function is at this particular point, f(a).

Limits are essential to calculus and mathematical analysis and the understanding of how functions behave. The concept of a limit can be written or expressed as: $\lim_{x \to a} f(x) = L.$ This is read as “the limit of f as x approaches a equals L”. This means that the value of the function f can be made arbitrarily close to L (and I mean as close as you want, e.g., L ± 0.1, L ± 0.01, L ± 0.001, you get the idea 😄), by choosing values of x sufficiently close to a.

Let’s consider f(x) = 2x² - 3x + 1 and calculate $\lim_{x \to 2} 2x^2 -3x +1$. As x approaches 2, f(x) approaches 2·(2)² - 3·(2) + 1 = 2·4 -3·2 + 1 = 3.

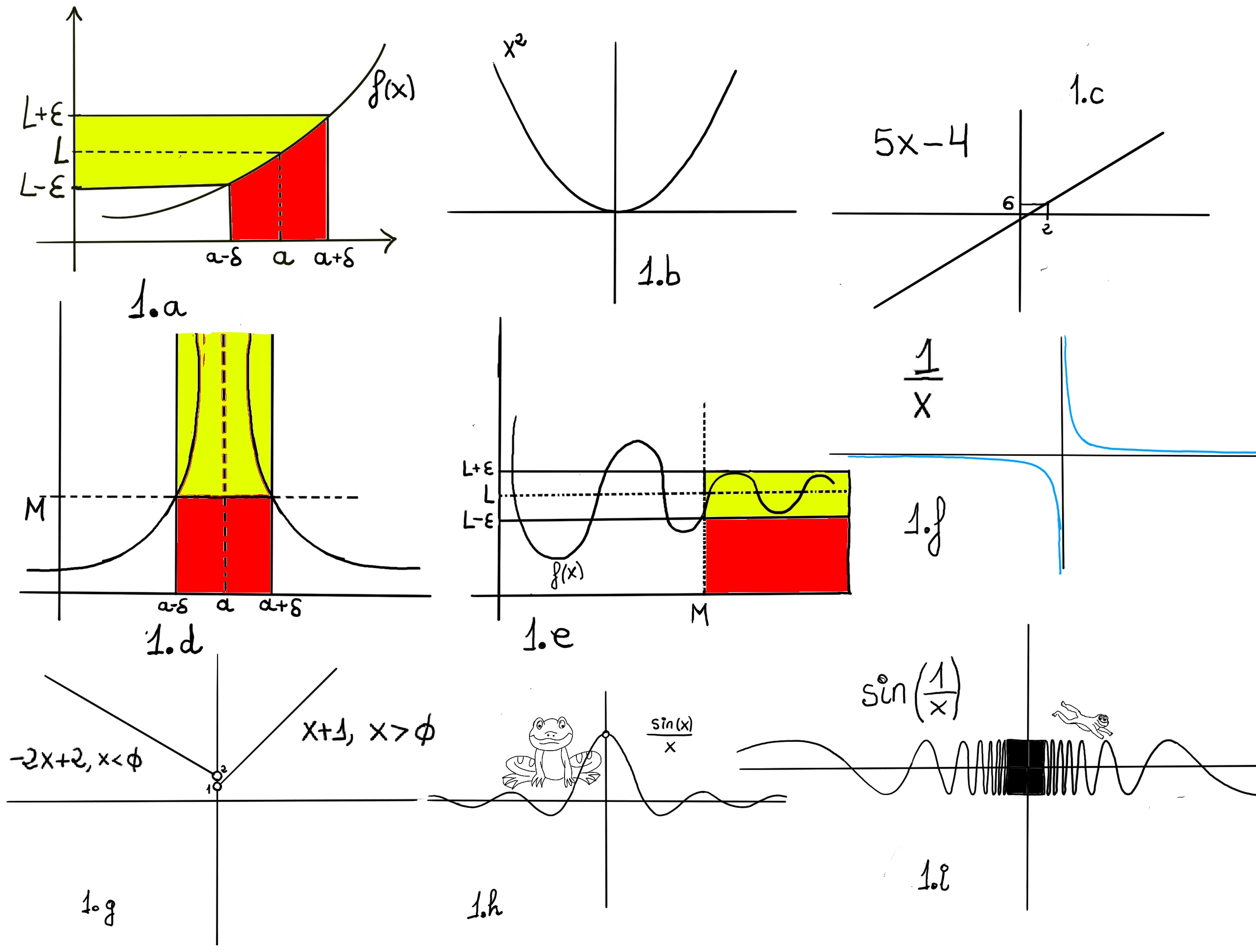
If you evaluate the function x² at x = 0, the function equals 0, and $\lim_{x \to 0} x^2 = 0$ (Figure 1.b). Similarly, $\lim_{x \to 2} 5x -4 = 5·2 -4 = 6$ (Figure 1.c).

• Consider the function $g(x) = \frac{x^2-1}{x-1}$, g(x) is a line, namely x + 1, but the function is undefined at x = 1. Dom(g) = ℝ - {1}. However, $\lim_{x \to 1} \frac{x^2-1}{x-1} = \lim_{x \to 1} \frac{(x-1)(x+1)}{x-1} = \lim_{x \to 1} x +1 = 2.$ To be honest, the function is begging to be redefined as f(x) = x + 1, and then Dom(f) = ℝ.

• $f(x) = \begin{cases} 3x + 1, &x ≠ 2\\\\ 2, &x < 0 \end{cases}$

$\lim_{x \to -2} f(x) = -5.$

• Let $f(x) = \begin{cases} -2x + 2, &x < 0 \\ x + 1, &x > 0 \end{cases}$ (Figure 1.g.)

Approaching 0 from the left (x < 0), f(x) becomes -2x + 2 and we get closer and closer to 2. Approaching 0 from the right (x > 0), f(x) becomes x + 1 and we get closer and closer to 1.

Therefore, $\lim_{x \to 1} f(x)$ does not exist because the left and right limits are different.

How To Evaluate Limits From a Graph

Consider f(x) = $\frac{sin(x)}{x}$ (1.h) and observe its graphical representation. Examine the graph as x gets closer and closer to the specified value. If the function approaches a specific value as x gets closer to the point, that value is the limit, e.g., $\lim_{x \to 0} \frac{sin(x)}{x} = 1$

If the function approaches positive or negative infinity, the limit is +∞ or -∞, respectively, e.g., $\lim_{x \to a} f(x) = +∞$ (Figure 1.d), $\lim_{x \to 0⁺} \frac{1}{x} = +∞$, $\lim_{x \to 0⁻} \frac{1}{x} = -∞$ (Figure 1.f). The right limit ($\lim_{x \to 0⁺} \frac{1}{x}$) means you approach the point x = 0 from the right, i.e., with values bigger than 0. The left limit ($\lim_{x \to 0⁻} \frac{1}{x}$) means you approach the point x = 0 from the right, i.e., we must take values lower than 0, hence $\lim_{x \to 0} \frac{1}{x}$ is undefined.

If the function oscillates or does not approach a specific value, the limit does not exist, e.g., $\lim_{x \to a} sin(\frac{1}{x})$ D.N.E. (does not exist, Figure 1.i).

Precise definition

One would say that the limit of f, as x approaches a, is L. Formally, for every real ε > 0, there exists a real δ > 0 such that for all real x, 0 < | x − a | < δ implies that | f(x) − L | < ε. In other words, f(x) gets closer and closer to L, f(x)∈ (L-ε, L+ε), as x moves closer and closer -approaching closer but never touching- to a (x ∈ (a-δ, a+δ), x≠a)) -Fig 1.a.-

Definition. Let f(x) be a function defined on an interval that contains x = a, except possibly at x = a, then we say that, $\lim_{x \to a} f(x) = L$ if

$\forall \epsilon>0, \exists \delta>0: 0<|x-a|<\delta, implies~ |f(x)-L|<\epsilon$

Or

$\forall \epsilon>0, \exists \delta>0: |f(x)-L|<\epsilon, whenever~ 0<|x-a|<\delta$  

Solved easy exercises

• $\lim_{x \to -2} \frac{x^2-x-2}{x+2} = \lim_{x \to -2} \frac{(x-1)(x+2)}{x+2} = \lim_{x \to -2} (x-1) = -3$.

  Finding a limit by factoring is a technique to computing limits that works by canceling out common factors. It allows us to transform an indeterminate form into one that allows for direct evaluation. Notice that the limit as x approaches -2 has nothing no to do with the value of the function at x = -2.

• $\lim_{x \to 2}\frac{x^2-4}{x-2} =\lim_{x \to 2}\frac{(x+2)(x-2)}{x-2} = \lim_{x \to 2}(x+2)=4 $
• $\lim_{x \to 4} x^{2} + x -11 = 9.$
• $\lim_{x \to 4} \frac {x + 3}{x^{2} + 12} = 0.25.$
• $\lim_{x \to 4} \frac{\sqrt{x}-2}{x-4} = \lim_{x \to 4} \frac{(\sqrt{x}-2)(\sqrt{x}+2)}{(x-4)(\sqrt{x}+2)} = \lim_{x \to 4} \frac{x-4}{(x-4)(\sqrt{x}+2)} = \lim_{x \to 4} \frac{1}{\sqrt{x}+2} = \frac{1}{4}.$
• $\lim_{x \to 0} \frac{x}{3-\sqrt{x+9}} = \lim_{x \to 0} \frac{x(3+\sqrt{x+9})}{(3-\sqrt{x+9})(3+\sqrt{x+9})} = \lim_{x \to 0} \frac{x(3+\sqrt{x+9})}{9-x+9} = \lim_{x \to 0} \frac{x(3+\sqrt{x+9})}{-x} = \lim_{x \to 0} -(3+\sqrt{x+9}) = -(3+3) = -6.$
• $\lim_{x \to -2} \frac{x^2+5x+6}{x^2+6x+8} = \lim_{x \to -2} \frac{(x+2)(x+3)}{(x+2)(x+4)} = \lim_{x \to -2} \frac{(x+3)}{(x+4)}=\frac{1}{2}.$

Solved examples with epsilon-delta proofs

• $\lim_{x \to 0} x^{2} = 0$ -1.b.-

$\forall \epsilon>0, \exists \delta>0: 0<|x|<\delta, implies~ |x^{2}|<\epsilon$

Let’s choose $\delta = \sqrt \epsilon, then$ $\forall \epsilon>0, \exists \delta>0: 0<|x|<\sqrt \epsilon, implies~ |x^{2}|<\epsilon$

That’s true because $|x^{2}|=|x|^{2}<(\sqrt \epsilon)^{2} = \epsilon$

• $\lim_{x \to 2} 5x - 4 = 6$ -1.c.-

$\forall \epsilon>0, \exists \delta>0: 0<|x-2|<\delta,~implies~ |5x - 4 -6|<\epsilon$

$\forall \epsilon>0, \exists \delta>0: 0<|x-2|<\delta,~implies~ 5|x - 2|<\epsilon$ because |5x -4 -6| = |5x-10| = |5·(x-2)| = |5||x-2| = 5|x-2|.

Let’s choose $\delta = \frac {\epsilon}{5}$, then

$\forall \epsilon>0, \exists \delta>0: 0<|x-2|<\frac {\epsilon}{5},~implies~ 5|x - 2|<\frac {5\epsilon}{5} = \epsilon$

• $\lim_{x \to 4} (2x -3) = 5$

$\forall \epsilon>0, \exists \delta>0: 0<|x-4|<\delta,~implies~ |2x - 3 -5|<\epsilon$

$|2x - 3 -5|<\epsilon ↭ 2|x-4|$ ⇒[Let δ = ε/2] $|2x - 3 -5| = 2|x-4| < 2\frac{\epsilon}{2} = \epsilon$

• $\lim_{x \to 5} (\frac{1}{x-3}) = \frac{1}{2}$

$\forall \epsilon>0, \exists \delta>0: 0<|x-5|<\delta,~implies~ |\frac{1}{x-3} -\frac{1}{2}|<\epsilon$

$|\frac{1}{x-3} -\frac{1}{2}| = |\frac{2-x+3}{2(x-3)}| = |\frac{-x+5}{2(x-3)}| = \frac{1}{2}·|x-5|·\frac{1}{|x-3|}$ 🚀

We know that $0<|x-5|<\delta$. Let’s choose δ < 1, |x-5| < δ ↭ -1 < x -5 < 1 ↭[Let’s add 2] 1 < x -3 < 3 ⇒ $\frac{1}{3} < \frac{1}{x-3} < 1 ⇒ -1 < \frac{1}{3} < \frac{1}{x-3} < 1 ⇒ -1 < \frac{1}{x-3} < 1 ⇒ |\frac{1}{x-3}| < 1 ⇒ \frac{1}{|x-3|} < 1$

[🚀] $|\frac{1}{x-3} -\frac{1}{2}| = \frac{1}{2}·|x-5|·\frac{1}{|x-3|} < \frac{1}{2}·δ·1$ [So we pick δ = min{1, 2ε}] ≤ $\frac{1}{2}·2ε·1 = ε$∎

• $\lim_{x \to 0} xsin(\frac {1}{x}) = 0.$

$\forall \epsilon>0, \exists \delta>0: 0<|x|<\delta,~implies~ |xsin(\frac {1}{x})|<\epsilon$

Let’s choose δ = ε, then $0<|x|<\delta,~implies~ |xsin(\frac {1}{x})| = |x|·|sin(\frac {1}{x})| ≤ |x|< δ = ε$∎

• $\lim_{x \to 2} 3x^2 = 12$

$\forall \epsilon>0, \exists \delta>0: 0<|x-2|<\delta,~implies~ |3x^2 -12|<\epsilon$

$|3x^2 -12| = 3|x^2-4| = 3|(x-2)(x+2)| = 3|x-2||x+2|$ < [🚀]

Let’s choose δ = min{1, something else -be patience😄-}, |x-2| < 1 ↭ -1 < x -2 < 1 ⇒[Let’s add 4] 3 < x + 2 < 5 ⇒ -5 < 3 < x + 2 < 5 ⇒ |x + 2| < 5

< [🚀] 3·δ·5 <[Let’s choose δ = min{1, ε/15}] ε∎

• $\lim_{x \to 5} \sqrt{3x+1} = 4$

$\forall \epsilon>0, \exists \delta>0: 0<|x-5|<\delta,~implies~ |\sqrt{3x+1} - 4|<\epsilon$

$|\sqrt{3x+1} - 4| = |\frac{(\sqrt{3x+1} - 4)(\sqrt{3x+1} + 4)}{\sqrt{3x+1} + 4}| = |\frac{3x+1-16}{\sqrt{3x+1} + 4}| = |\frac{3x-15}{\sqrt{3x+1} + 4}|$=[Choose δ < 1, x is between 4 and 6 and the denominator is not only positive, but greater than 1] $\frac{3|x-5|}{\sqrt{3x+1} + 4}$ [$\sqrt{3x+1} + 4>1 ⇒ \frac{1}{\sqrt{3x+1} + 4} < \frac{1}{1}$] 3|x-5| < 3δ =[Choose δ = min{1, ε/3}] ε ∎

• $\lim_{x \to -2} -3x+5 = 11$

$\forall \epsilon>0, \exists \delta>0: 0<|x+2|<\delta,~implies~ |-3x+5 - 11|<\epsilon$

|-3x+5 - 11| = |-3x -6| = |-3(x + 2)| = 3|x+2| < 3·δ =[Choose δ = ^ε⁄₃] ε∎

• $\lim_{x \to 3} \frac{x}{x-2} = 3$

$\forall \epsilon>0, \exists \delta>0: 0<|x-3|<\delta,~implies~ |\frac{x}{x-2} - 3|<\epsilon$

$|\frac{x}{x-2} - 3| = |\frac{x-3x+6}{x-2}| = |\frac{-2x+6}{x-2}|=2|x-3|\frac{1}{|x-2|} < 2δ\frac{1}{|x-2|}$ [🚀]

|x-3|<δ ⇒[Choose δ = min{1/2, something else}] $\frac{-1}{2}< x-3 < \frac{1}{2}$ ⇒[Add 1] $\frac{1}{2}< x-2 < \frac{3}{2} ⇒ 2 > \frac{1}{x-2} > \frac{2}{3} > -2 ⇒ \frac{1}{|x-2|}< 2$

[🚀] $|\frac{x}{x-2} - 3|$ < 2·δ·2 <[Choose δ = min{1/2, ε/4}] ε∎

• $\lim_{x \to 2} x^3 = 8$

$\forall \epsilon>0, \exists \delta>0: 0<|x-2|<\delta,~implies~ |x^3 - 8|<\epsilon$

$|x^3 - 8| = |x-2|·|x^2+2x+4|< δ·|x^2+2x+4|$ [🚀]

Choose δ = min{1, something else}, |x-2|< 1 ↭ -1 < x -2 < 1 ⇒[Adding 2] 1 < x < 3 ⇒ -3 < 1 < x < 3 ⇒ |x| < 3.

$|x^3 - 8| 🚀< δ·|x^2+2x+4|≤$ [By the triangle inequality, |a+b| ≤ |a| + |b|] δ·(|x²|+|2x|+|4|) < δ(3² +2·3 + 4) = δ·19 [Choose δ = min{1, ε/19}] ε ∎

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus.
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. YouTube’s Andrew Misseldine: Calculus, College Algebra and Abstract Algebra.
8. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.
9. blackpenredpen.