Impossible Geometric Constructions.

5th Law, Males can love females, but not understand them and have delusions of adequacy and conceit. On the other hand, females are crazy. The reason why females are crazy is because their male partners make them want to chew their veins violently and without mercy. Both are told that they are equal, to be strong, independent, and fearless, to be whatever they want, and fulfill their dreams to the fullest (real dialogue that reaches for compromise and adapting to reality are for sissies) but more and more people feel hopeless, depressed, and alone, Apocalypse, Anawim, #justtothepoint.

Reclaim

Definition. If F is a subfield of a field E, then E is called an extension field of F, denoted E/F or E:F Example, E = ℝ, F = ℂ, ℂ:ℝ.

Let E be an extension of F,

1. Then, E is a vector space over F.
2. E will have a basis set.
3. The dimension of E considered as a vector space over F is called the degree of E over F and denoted as [E:F].

The extension is said to be finite if [E:F] is finite, its base could be counted. Otherwise, if [E:F] is infinite, the extension is said to be infinite, ∞.

Theorem. Let F ⊆ E ⊆ K be a tower of fields. If [K:E] < ∞ and [E:F] < ∞ then, (i) [K:F] < ∞, and (ii) [K:F] = [K:E]·[E:F]

Theorem. Let p(x) be an irreducible polynomial in F[x] and let u be a root of p(x) in an extension E of F. Then,

(i) F(u), the subfield of E generated by F and u is the set, that is, the smallest field containing F and u, is indeed F[u] = {b₀ + b₁u + ··· + b_mu^m ∈ E | b₀ + b₁x + ··· + b_mx^m ∈ F[x]}

(ii) If the degree of p(x) is n, the set {1, u, ···, u^n-1} forms a basis of F(u) over F, i.e., each element of F(u) can be written uniquely as c₀ + c₁u + ··· + c_nu^n-1 where c_i ∈ F, and [F(u):F] = n.

Definitions. An element α ∈ E is algebraic over F if there exists a non-constant polynomial p(x) ∈ F[x] such that p(α)=0, i.e., α is the root of p(x).

The minimal polynomial of u over E

Theorem. Let E be an extension field of F, and let u ∈ E be algebraic over F. Let p(x) ∈ F[x] be a polynomial of least degree such that p(u) = 0, we call p the minimal polynomial of u over E, Then,

(i) p(x) is irreducible over F
(ii) if g(x) ∈ F[x] is such that g(u) = 0, then p(x) | g(x)
(iii) There is exactly one monic polynomial p(x) ∈ F[x] of least degree such that p(u) = 0. This monic polynomial always exists because we can always divide it by its leading coefficient, and still u be a root.

Theorem. If f ∈ F[x] is monic, irreducible (it cannot be written as a product of non constant polynomials),and f(α)= 0, then f is the minimal polynomial of α.

Besides, if E is an extension of F and α ∈ E is algebraic over F, then F(α) is an algebraic extension of F and deg(F(α):F)=deg(p(x)) where p is the minimal polynomial of α.

Introduction

Plato believed that the only perfect geometric figures were the straight line and the circle. Therefore, the ancient Greek were interested in constructions that could be achieved using rulers (the ruler is not marked so we cannot use it to measure things, so it is an unmarked straightedge) and compasses, such as an equilateral triangle (Figure 1.a.), a square, or a regular pentagon or hexagon, and wondered if it was possible to use them to:

1. Square the circle, that is, construct a square that has an area equal to that of a given circle.
2. Double the cube, that is, construct a new cube having twice the volume of the given one.
3. Trisect an angle.

Proposition. Suppose that P = (α, β) can be constructed from P₁ = (a₁, b₁),···, P_n = (a_n, b_n) using rules and compass. Then, α and β can be obtained from a₁, ···, a_n, b₁, ···, b_n by repeated use of field operations +, -, ·, ÷, and √. Let F ⊆ K be a field generated by rule and compass constructions where P₁,···, P_n live. Suppose P is constructed by ruler and compass from F in one single step, then [F(α): F] ≤ 2.

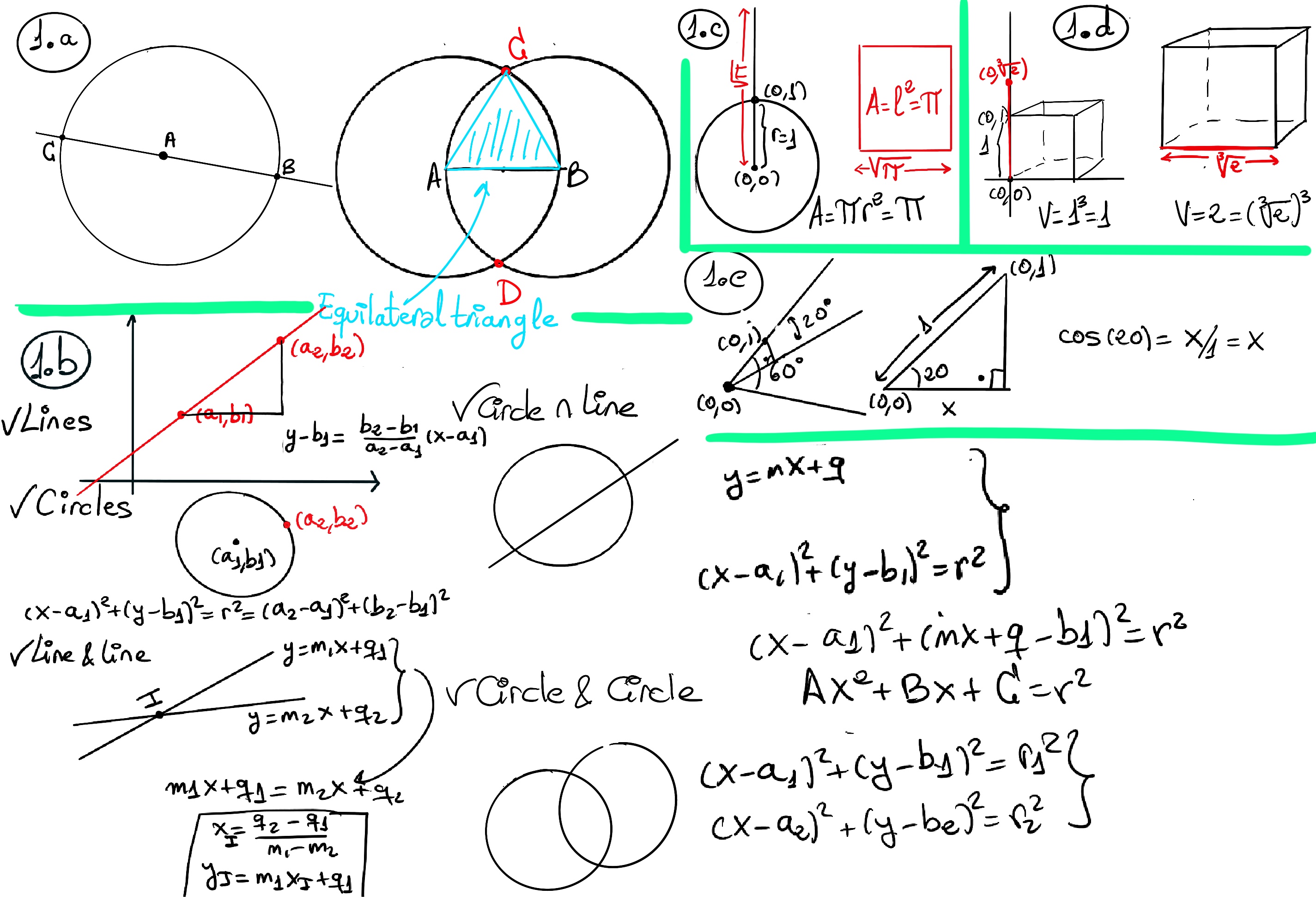
Proof. (Figure 1.b.)

• Lines: $y-b_1=\frac{b_2-b_1}{a_2-a_1}(x-a_1)$. The solution lies in F.
• Circles: $(x-a_1)^2+(y-b_1)^2=r^2=(a_2-a_1)^2+(b_2-b_1)^2$
• Intersect line and line: y = m₁x + q₁, y = m₂x + q₂ ⇒ m₁x + q₁ = m₂x + q₂ ⇒ $x_I = \frac{q_2-q_1}{m_1-m_2}, y_I=m_1x_I+q_1$
• Intersect circle and line: y = mx + q, (x -a₁)² + (y -b₁)² = r² ⇒ (x -a₁)² + (mx + q -b₁)² = r², basically we will obtain an equation Ax² + Bx + C = r² where x can be obtained from existing quantities using the field operations +, -, ·, ÷, and √. Therefore, the solution lies in a quadratic extension of F.
• Intersection of two circles. (x -a₁)² + (y -b₁)² = r₁² and (x -a₂)² + (y -b₂)² = r₂² where x can be obtained from existing quantities using the field operations +, -, ·, ÷, and √.

Let F ⊆ K be a field generated by ruler and compass. Suppose α is constructible from F in one step, we have shown that [F(α) : F] ≤ 2. In other words, constructing a number α ∉ F in one step amounts to taking a degree-2 extension of F.

Proposition. If P = (α, β) can be constructed from (0, 0) and (0, 1), then α and β can be obtained from 0, 1 by repeatedly applying +, -, ·, ÷, and √ (there is nothing new up to here).

Theorem. A real (or complex) number α is constructible if and only if there is a tower of fields ℚ = $\mathbb{F}_0⊆\mathbb{F}_1⊆\mathbb{F}_2⊆···⊆\mathbb{F}_K⊆ℝ$ such that α ∈ $\mathbb{F}_k,~ and~ \mathbb{F}_i=\mathbb{F}$_i-1($\sqrt{a_i}) ↭ [\mathbb{F}_i: \mathbb{F}_{i-1}]≤2,~a_i∈\mathbb{F}$_i-1. The degree of $\mathbb{F}_i:ℚ$ will then be a power of 2 (it could be 2⁰=1 if $\sqrt{a_i}$ is already in $\mathbb{F}_i$ or 2¹=2).

Corollary. If α is constructable, then ℚ(α):ℚ has degree 2^k for some k ∈ ℕ, [ℚ(α) : ℚ] = 2^k.

Proof.

By the previous theorem, α ∈ $\mathbb{F}_k, deg(\mathbb{F}_k:ℚ)=2^m, m∈ℕ$.

Since α ∈ $\mathbb{F}_k,~ and~ ℚ⊆\mathbb{F}_k⇒ ℚ(α)⊆\mathbb{F}_k⇒deg(\mathbb{F}_k:ℚ(α))·deg(ℚ(α):ℚ)=deg(\mathbb{F}_k:ℚ))=2^m⇒deg(ℚ(α):ℚ)=2^k,k ≤ m$ ∎

Theorem. It is impossible to square the circle.

Proof.

Fact: π is transcendental over ℚ ⇒ $\sqrt{π}$ is transcendental over ℚ.

If we can square the unit circle ⇒[Figure 1.c., A = πr² =[r = 1] π = l²] $\sqrt{π}$ is constructable ⇒[Corollary. If α is constructable, then ℚ(α):ℚ has degree 2^k for some k ∈ ℕ, [ℚ(α) : ℚ] = 2^k.] deg($ℚ(\sqrt{π}):ℚ)=2^k$

We claim that deg($ℚ(\sqrt{π}):ℚ)=∞$

Let’s suppose by reduction to the absurd, that $deg(ℚ(\sqrt{π}):ℚ)=m$ ⇒ $1, \sqrt{π}, \sqrt{π}^2, \sqrt{π}^3, ···, \sqrt{π}^{m-1}$ is linear independent over ℚ ⇒ ∃q_i ∈ ℚ_i, not all zeros: $q_0·1 + q_1\sqrt{π}+···q_m\sqrt{π}^{m-1}=0$, hence consider f(x) = $\sum_{i=0}^{m-1} q_ix^i$, q_i ∈ ℚ_i, not all zeros ⇒ π is algebraic, f(π)=0 ⊥

Theorem. It is impossible to double every cube.

Proof.

If this were possible ⇒ [Figure 1.d., Volume of the unit cube V = a³ = 1, doubling the volumen = 2 = $(\sqrt[3]{2})^3$] $\sqrt[3]{2}$ is constructable, hence $deg(ℚ(\sqrt[3]{2}):ℚ)=2^k$.

We claim $deg(ℚ(\sqrt[3]{2}):ℚ)$ =[Corollary. If α is constructable, then ℚ(α):ℚ has degree 2^k for some k ∈ ℕ, [ℚ(α) : ℚ] = 2^k] $2^k$ = 3 ⊥ because x³ -2 is the minimal polynomial of $\sqrt[3]{2}$ over ℚ. It is monic, $\sqrt[3]{2}$ is the root x³ -2, and irreducible over ℚ.

Let’s suppose x³-2 factors in ℚ: x³ -2 = [These two polynomials need to be monic because x³ -2 is monic] (x² +ax + b)(x + c) ⇒ (x + c) = 0, -c is a root, and therefore, (-c)³ -2 = 0 ⇒ -c³ = 2, -c =[-c ∈ ℚ] c₁/c₂, where c₁, c₂ ∈ ℤ, and we can assume that they do not have any factors in common; otherwise, we could cancel them out.

Futhermore, (c₁/c₂)³ = 2 ⇒ c₁³ = 2c₂³ ⇒ c₁³ is even ⇒ c₁ is even, so c₁=2r, c₁³=2³r³ = 2c₂³ ⇒ c₂³ = 2²r³ ⇒ c₂³ is even ⇒ c₂ is even ⊥ (we have previously assumed that c₁ and c₂ do not have any factors in common).

Theorem. It is impossible to trisect every angle.

Proof.

If we can trisect 60° ⇒ [Figure 1.e. considering a triangle with α = 20°, h = 1] x=cos(20°) would be constructive ⇒[Corollary. If α is constructable, then ℚ(α):ℚ has degree 2^k for some k ∈ ℕ, [ℚ(α) : ℚ] = 2^k] deg(ℚ(cos(20°):ℚ) = 2^k.

By trigonometry, cos(3θ) = 4cos³(θ) -3cos(θ). In particular, 1/2 = cos(3·20°) = 4cos³(20°) - 3cos(20°), so f(x) = 4x³ -3x -1/2 has a root, namely cos(20°) ⇒ 2·f(x) = 2·4x³ -3·2x -1 has a root, namely cos(20°) ⇒ g(x) = (2x)³ -3(2x) -1 has a root, cos(20°) ⇒[Let’s say y = 2x] y³ - 3y -1 has a root, namely 2·cos(20°).

We claim that y³ -3y -1 is monic, irreducible (it is left to the reader), and has the root 2·cos(20°) ⇒ deg(ℚ(2·cos(20°):ℚ) = 3 but ℚ(2·cos(20°)) is the same field extension as ℚ(cos(20°)), and therefore deg(ℚ(cos(20°):ℚ) = 3 because we are multiplying cos(20°) by an element 2 of the field (2 ∈ ℚ) ⊥ deg(ℚ(cos(20°):ℚ) = 2^k = 3.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.