Frieze and Wallpaper Groups

Hell is empty and all the devils are here, William Shakespeare.

A discrete frieze group consists of a pattern of finite width and height that is repeated over and over, endlessly, in both directions along its baseline to form a strip or pattern of infinite length by finite height. It is used for decorative strips and patterns on jewelry, sculpture, and architecture.  

For example, we might have the finite pattern $\textbf F$ and the following baseline:

It produces the infinite pattern

···$\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F\textbf F~···$

The symmetry group of this pattern of $\textbf F$'s consists of translations only. Let x denote the translation to the right of one unit, that is, the distance between two consecutive $\textbf F$’s, and we could express this symmetry group as follows,

F₁ = {xⁿ | n ∈ ℤ}. So for each integer, there is a corresponding translation and the frieze group associated with this pattern is the integers, (ℤ, +). All discrete frieze groups are infinite and have a subgroup isomorphic to ℤ generated by the translation that slides the frieze lengthwise until the basic pattern is superimposed on the position of its next neighbor pattern in that direction.

Consider integral signs space equal distance apart and continuing infinitely in both directions $\int$. This symmetry group is generated by a translation τ sliding the plane one unit to the right, and by a rotation ρ of 180° about a point in the center of the pattern. Notice that there are no horizontal or vertical reflections, and no glide reflections.

The n-th dihedral group is generated by two elements that do not commute, a rotation ρ = $\frac{2π}{n}$ of order n and a reflection τ of order 2, both satisfying τρ = ρτ^-1. D_∞ is used to describe this non-Abelian frieze group generated by τ of infinite order and ρ of order 2.

$\int~\int~\int~\int~\int~\int~\int~\int~\int~\int~\int~\int~\int~\int~\int~\int~\int~$

Next, let us consider this pattern of $\textbf D$’s:

$\textbf D~\textbf D~\textbf D~\textbf D~\textbf D~\textbf D~\textbf D~\textbf D~\textbf D~\textbf D~\textbf D~\textbf D~\textbf D~\textbf D~\textbf D~\textbf D~$

This group is generated by a translation τ one step to the right and by a vertical reflection μ about a horizontal line through the center of the pattern. We can check that these group generators commute (τμ = μτ), and for each pair (x, y) where x is an integer and y is 0 or 1 (ℤ₂), there is a corresponding translation and rotation combination (μ or id) which is a symmetry of the pattern, and therefore the symmetry group is isomorphic to ℤ x ℤ₂.

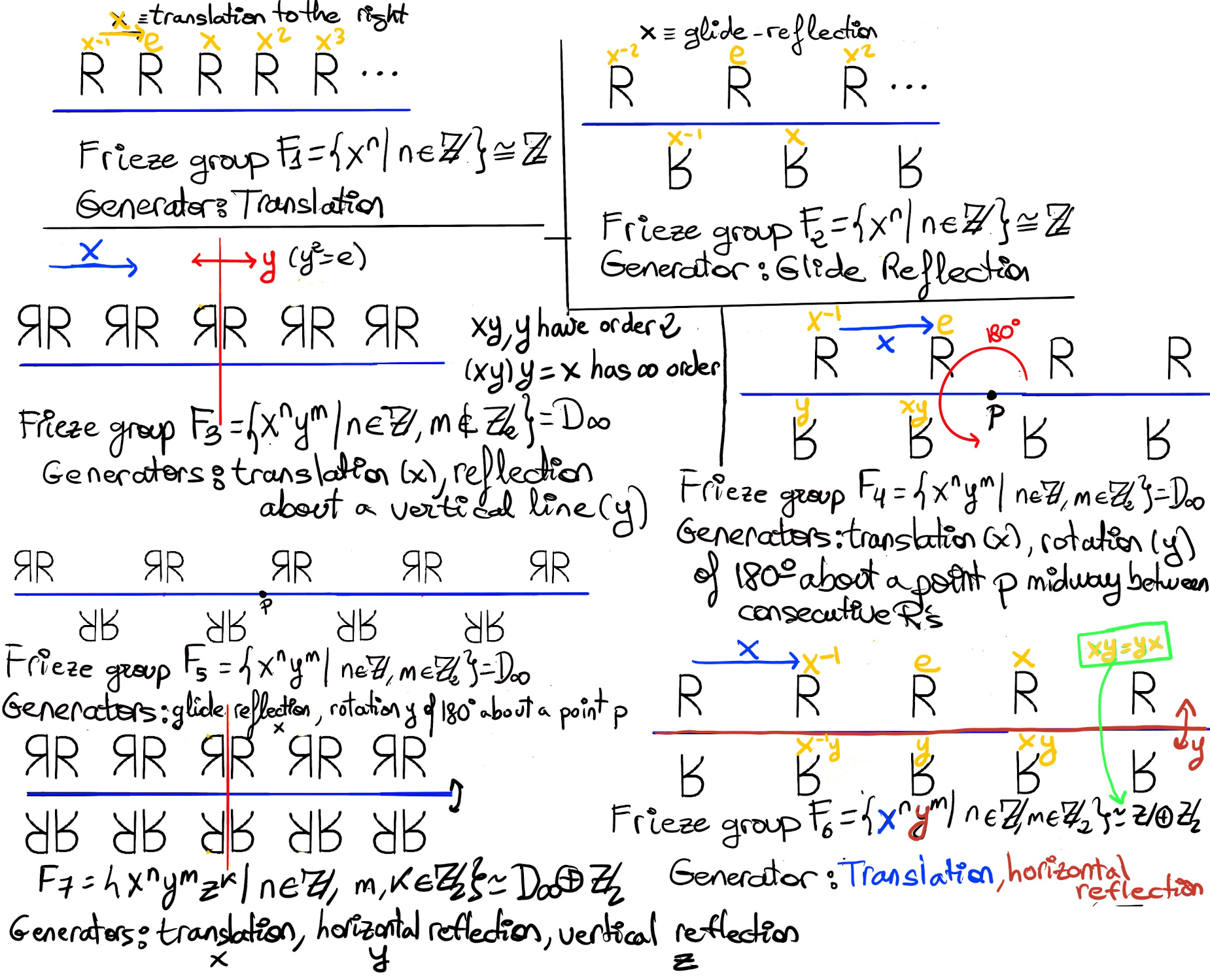
Theorem. The collection of discrete frieze groups consists precisely of the following four groups: ℤ, ℤ⊕ℤ₂, D_∞, and D_∞⊕ℤ₂. Since ℤ is a subgroup of D_∞, then each frieze group contains ℤ as a subgroup.

Wallpaper Groups

The frieze patterns include regular repetitions in one direction or dimension of a fundamental pattern. Therefore, the frieze groups include all powers of just a translation, and this is why ℤ is a subgroup of each frieze group.

If we consider regular repetitions in two directions or dimensions of a pattern, we will get a symmetry group which includes all powers of two translations. Such a symmetry group is called a wallpaper or crystallographic group, that is, the symmetry groups of plane patterns whose subgroups of translations are isomorphic to ℤ⊕ℤ. These patterns could be seen in architecture and decorative art, especially in textiles, tessellations, tiles, and wallpapers.

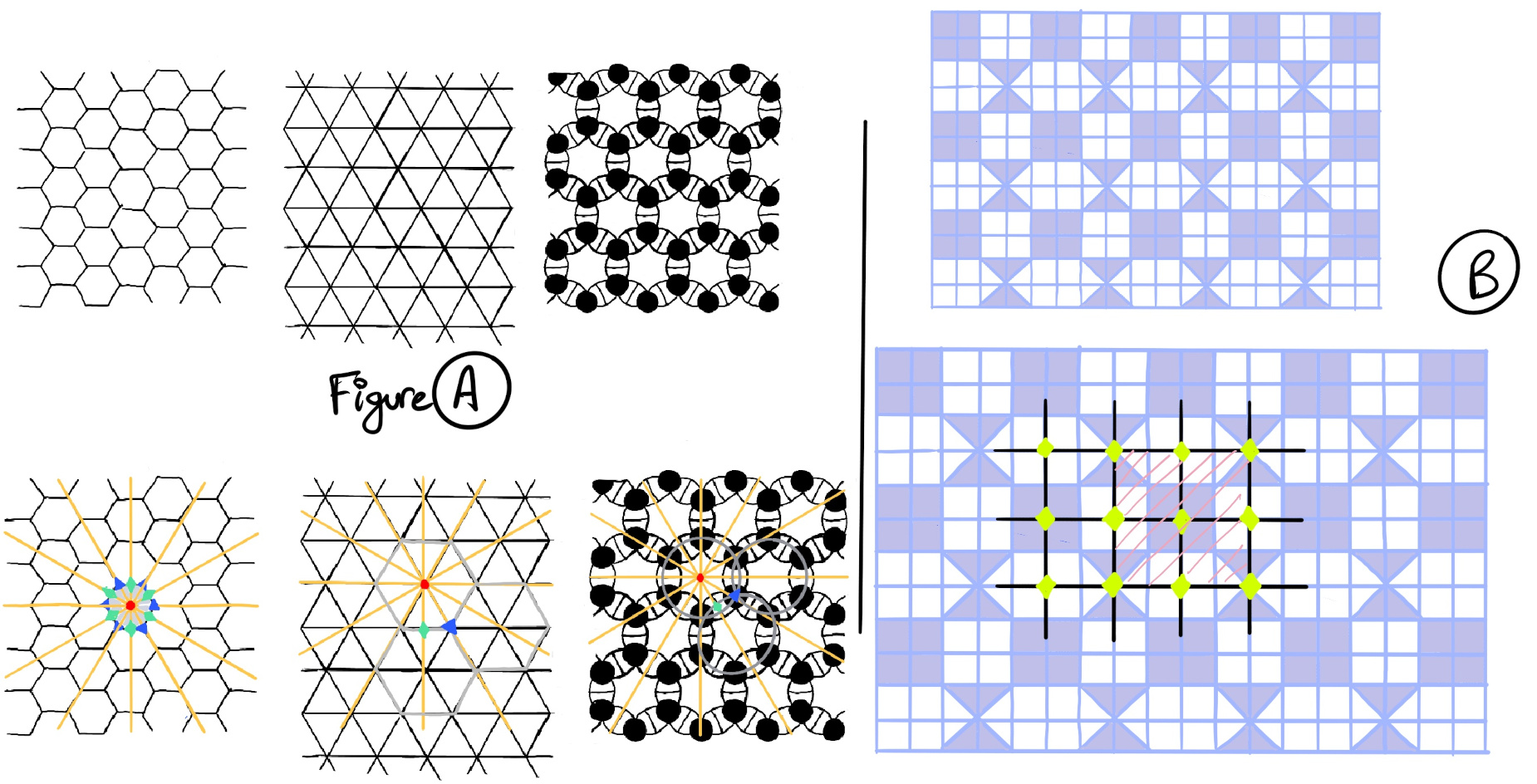
Observe the following illustration (Figure A). These three pattern look superficially quite different, but they have the same symmetric structure, that is, they share the same rotations and with the same order, reflections, translations, and glide reflections, and relations between them. They are wallpaper patterns with the same symmetric group, p6m. This group has one rotation centre of order six (60°), reflections in six distinct directions, two distinct rotation centers of order three, and three distinct centers of order two.  

Definitions.

• A Bravais lattice is an infinite array of discrete points generated by a set of discrete translation operations. They have an arrangement and orientation that appear the same no matter from which orientation you look at it. In two dimensions, there are five lattice types or Bravais lattices: oblique, hexagonal, square, primitive rectangular, and centered rectangular (Figure 1.a.)

• A unit cell comprises the space between adjacent lattice points as well as any atoms in that space.
• A pattern is a repetitive parallelogram of minimal area in a determined position on the wallpaper.
• The classification of wallpaper symmetry groups is done by a process of elimination. The first crucial step is known as the crystallographic restriction: A rotation symmetry of a wallpaper pattern must be a rotation of order 2, 3, 4, or 6. (Figure 1.b.)

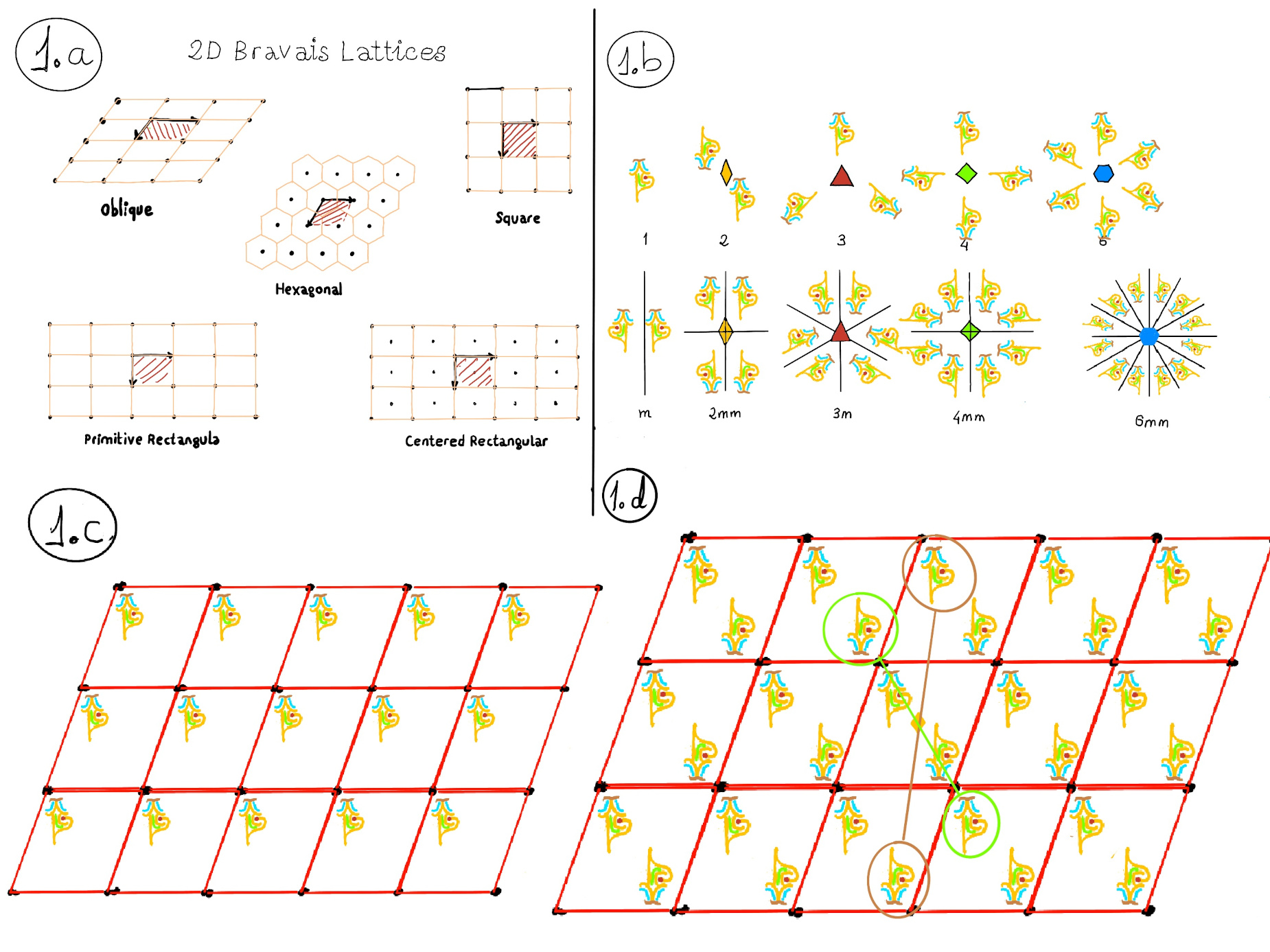
Let’s start by thinking about the translation symmetries. Observe a collection of lattice points in Figure 1.c. and a small pattern that is being translated in both dimensions. This is the symmetric group p1. This is the simplest of them all. It consists only of translations. The two translation axes may be inclined at any angle to each other.

Next, let’s put a center of rotation of order two (a two-fold rotation axis at the center of our cell) into the crystal (Figure 1.d). Observe that the application of both translation symmetries has not destroyed the two-fold rotation axes. Futhermore, there are additional two-fold rotation axes that are created by the translational symmetries. (Figure 2.a).

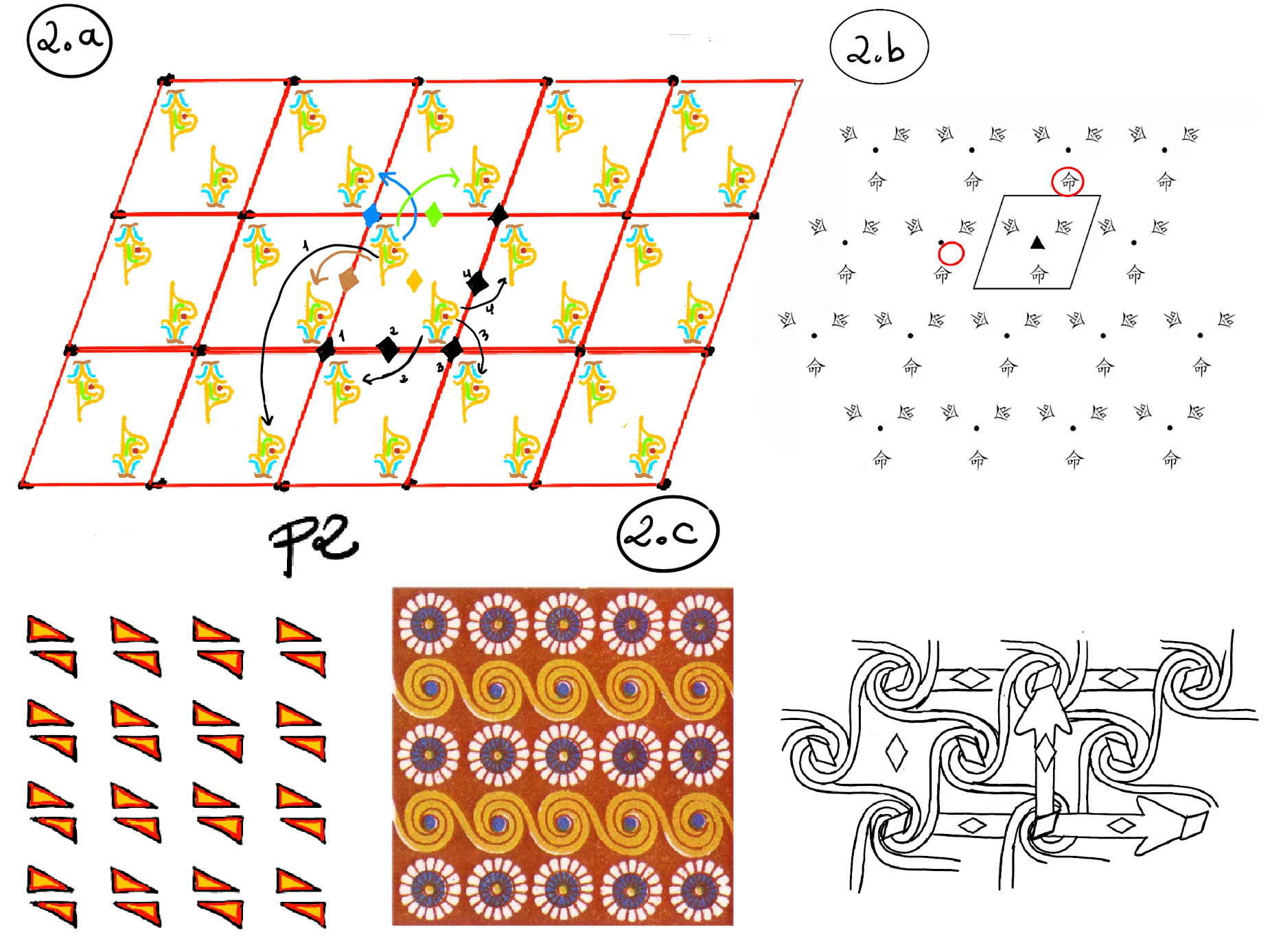
This is the symmetry group p2. It contains translations and 180° rotations, that is, rotations of order 2.Next, let’s observe that in an oblique lattice with a three-fold rotation axes at the center of the unit cell, the three-fold rotation axis is not retained when translations are applied (Figure 2.b.)

There are 17 wallpaper symmetry groups.

• p g. It contains translations and glide-reflections.The direction of the glide reflection is parallel to one axis of translation and perpendicular to the other axis of translation.
• pm. It contains translations and reflections. The axes of reflection are parallel to one axis of translation and perpendicular to the other axis of translation.
• The group pmg has two rotation centres of order 2 and reflections in only one direction. It has glide reflections whose axes are perpendicular to the reflection axes (Figure 3)

• cm. It contains no rotations. It has reflection axes, all parallel. There is at least one glide reflection, parallel to the mirror reflection axes, it is indeed halfway between two adjacent parallel reflection axes (Figure 4).

• p6 has 1 rotation centre of order 6, two rotation centres of order 3, 3 rotation centres of order 2. It has neither reflections nor glide reflections. For a full list see Wallpaper Groups by David E. Joyce and Wallpaper Group

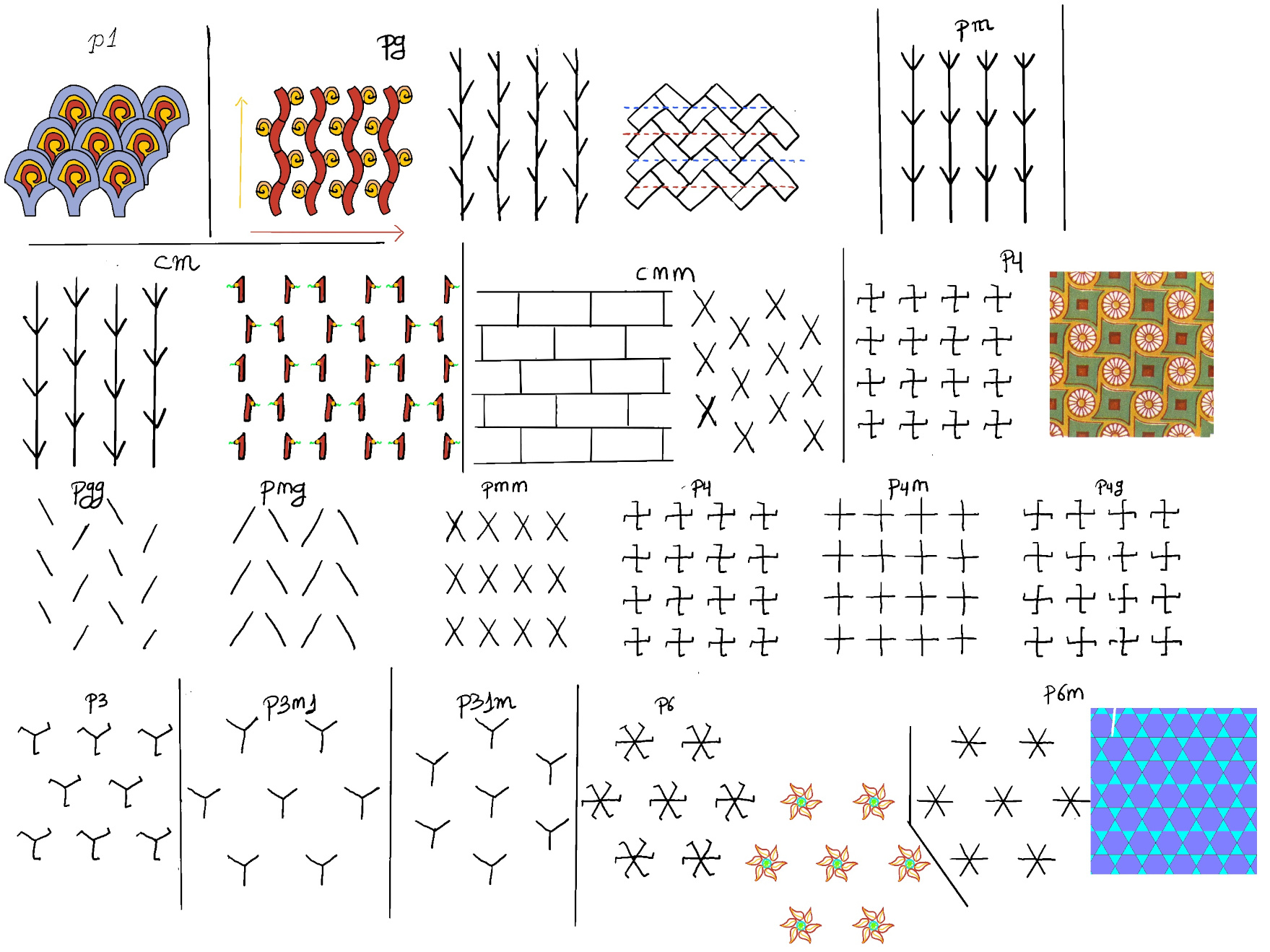
Exercise. What is the 2D plane group of this pattern (Figure B)?  

There are no four or six-fold rotation axes. This is pmm because it has reflections in two perpendicular directions, and four rotation centres of order two at the intersections of the reflection axes.

You may want to visit Wallpaper Symmetry. It let its users draw symmetric patterns in the plane.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.