Field Theory

“I mean to be positive and behave, but there are way too many options. Men think primarily with their penises, women care too much about money, and then women find themselves in soon-to-be-expired relationships with men who want to fuck their holes. Oh, that’s so rude, cold, and uncivilized of you to say, because, of course, how sophisticated, sweet, and romantic hole fucking really is,” I said, realizing that once brutal honesty has been deployed and executed, excuses are no longer an option, Apocalypse, Anawim, #justtothepoint.

Recall

1. A ring (R, +, ·). (i) (R, +) is an Abelian group: closure, associative, identity, inverses, and commutative. (ii) (R, .) closure and associative. (iii) Distributive laws.
2. A non-empty subset S of a ring R is called ideal of R is: ∀a, b ∈ S, r ∈ R ⇒ a - b ∈ S, ar ∈ S, ra ∈ S. Examples: {0} and R are trivial ideals.
3. An ideal A in a ring R is maximal if (i) A ≠ R, (ii) ∀B ideal B ⊇ A, either B = A or B = R.
4. Th. R/A is a field iff A is a maximal ideal.
5. Th. ⟨p(x)⟩ is maximal ↭ p(x) is irreducible. Let F be a field, p(x) be an irreducible polynomial over F, then F[x]/⟨p(x)⟩ is a field.

Characteristic of a field

A field F is a commutative ring with identity in which every nonzero element has an inverse or F^x = F -{0} is an Abelian group under multiplication.

Let 0_F and 1_F denote the additive and multiplicative identity of F respectively, then F is closed under addition by definition, and therefore, it contains 1_F + 1_F, 1_F + 1_F+ 1_F, and so on. These elements may not all be distinct. Let’s define n·1_F = 1_F + ··· + 1_F (n times).

We define the characteristic of a field F, char(F), as the smallest positive integer p such that p·1_F = 1 + 1 + ··· + 1 (p times) = 0 if such a p exists, or char(F) = 0 if 1 + 1 + ··· + 1 ≠ 0 ∀n ∈ N, e.g., char(ℝ) = char(ℚ) = 0; and for any prime p, $\mathfrak{F}_p=ℤ/pℤ$ has characteristic p.

We know that ∀n, m ∈ ℤ⁺,

1. n·1_F + m·1_F = (m + n)·1_F
2. (n·1_F)(m·1_F) = mn·1_F

Theorem. Let F be a field. Then, the characteristic of F is either zero or a prime number,

Proof.

Suppose for the sake of contradiction, char(F) = n, n ≠ 0 and n is not prime ⇒ ∃a, b ∈ F: n = ab, with n·1_F = 1 + 1 + ··_n·· + 1 + 1 = 0 ⇒ ab·1_F = 0 ⇒ (a·1_F)(b·1_F) = 0 ⇒ [A field is a ring with no zero divisors.] a·1_F = 0 or b·1_F = 0 ⊥ (char(F) = n). Therefore, the smallest positive integer p such that p·1_F = 1 + 1 + ··· + 1 (p times) = 0 if such a p exists, it is necessarily a prime. Futhermore, if n·1_F = 0, then n is divisible by char(F) = p, and p·n = n + n + ··· + n (p times) = n·1_F + n·1_F + ··· + n·1_F (p times) =[By assumption, n·1_F = 0] 0.

Let’s define (-n)·1_F = -(n·1_F) for n > 0, 0·1_F = 0, then we have the following ring homomorphism Φ: ℤ → F, defined as Φ(n) = n·1_F where ker(Φ) = char(F)ℤ.

If we take the quotient by the kernel gives us an injection of either ℤ (char(F) = 0) or ℤ/pℤ (char(F) = p). Since F is a field, it contains a subfield isomorphic either to ℚ (the field of fractions of ℤ) or to $\mathfrak{F}_p=ℤ/pℤ$ (the field of fractions of ℤ/pℤ). In either case, it is the smallest subfield of F containing 1_F, the prime subfield, that is, the field generated by the multiplicative identity 1_F of F, e.g., the prime subfield of both ℚ and ℝ is ℚ.

Field Extension

Definition. If F is a subfield of a field E, then E is called an extension field of F, denoted E/F or E:F. (Figure 1.a.)  

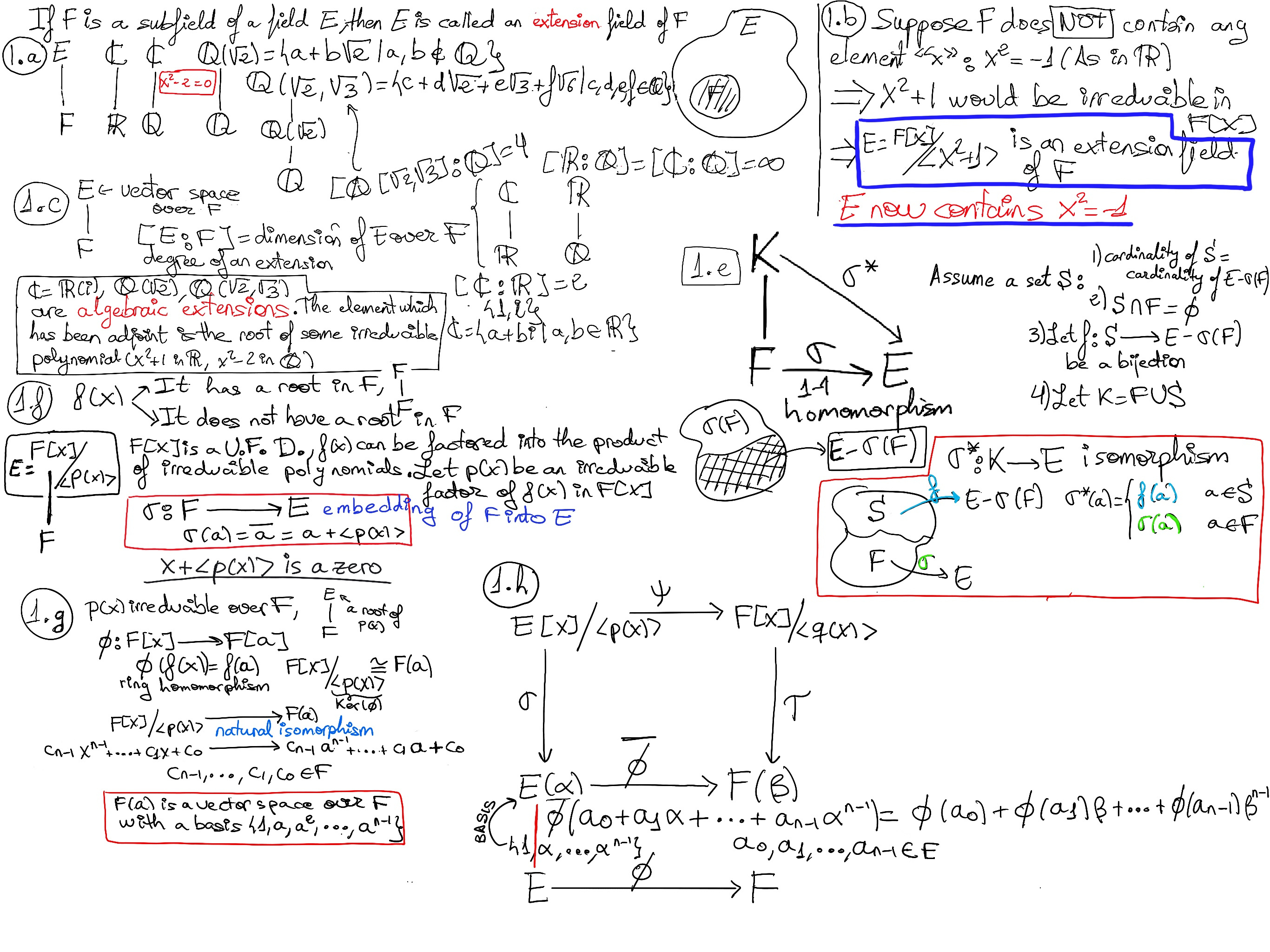
Examples.

• Every field is an extension of its prime subfield.
• ℂ is an extension of both ℝ and ℚ, ℝ is an extension of ℚ
• Let ℚ($\sqrt{2}$) = {$a+\sqrt{2}b|a, b ∈ ℚ$}. If we have a field, ℚ, and we want a field where the equation x² - 2 = 0 has a solution, we extend the field of rational to ℚ($\sqrt{2}$)
• ℚ($\sqrt{2},\sqrt{3}$) = {$a+\sqrt{3}b|a, b ∈ ℚ(\sqrt{2})$} = {$c+\sqrt{2}d+\sqrt{3}e+\sqrt{6}f|c, d, e, f ∈ ℚ$} is an extension field of ℚ.
• Similarly ℂ = ℝ(i) = {a + bi|a, b ∈ ℝ, i^2 = -1}, the complex number is an extension of ℝ that contains a zero of x² + 1, namely i.

Suppose that a field F does not contain any element x such that x² = -1 (as in ℝ), then the polynomial x² + 1 would be irreducible in F[x] ⇒ The ideal ⟨x² + 1⟩ would be maximal and E = F[x]/⟨x² + 1⟩ is an extension field of F that contains a root for x² = -1. Figure 1.b.

Similarly, we can construct splitting fields of any polynomial in F[x]. Let E be an extension of F, the given polynomial splits into a product of linear factors, e.g., a₀ + a₁x + ··· + a_nxⁿ = (x -α₁)(x -α₂) ··· (x -α_n)

Let E be an extension of F,

1. Then, E is a vector space over F.
2. E will have a basis set.
3. The dimension of E considered as a vector space over F is called the degree of E over F and denoted as [E:F]. Figure 1.c.

The extension is said to be finite if [E:F] is finite, its base could be counted. Otherwise, if [E:F] is infinite, the extension is said to be ∞.

Examples.

1. {1, i} is a basis of ℂ, dim_ℝ(ℂ) = [ℂ : ℝ] = 2.
2. [ ℝ : ℚ] = [ ℂ : ℚ] = Infinite
3. {1, $\sqrt{2}$} is a basis of ℚ($\sqrt{2}$) and [ℚ($\sqrt{2}$):ℚ] = 2
4. {1, $\sqrt{2}, \sqrt{3}, \sqrt{6}$} is a basis of ℚ($\sqrt{2}, \sqrt{3}$) and [ℚ($\sqrt{2}, \sqrt{3}$):ℚ] = 4, and [ℚ($\sqrt{2}, \sqrt{3}$):ℚ($\sqrt{2}$] = 2.

Consider that ℂ = ℝ(i), ℚ($\sqrt{2}$), ℚ($\sqrt{2}, \sqrt{3}$) are algebraic extensions. The elements which has been adjoint to these fields are the root of some irreducible polynomials (x² + 1 in ℝ, x² -2 in ℚ, (x² -2)(x² - 3) in ℚ respectively), and they are called algebraic elements.

Multiplicative property of degree extensions. Let F ⊆ E ⊆ K be a tower of fields. If [K:E] < ∞ and [E:F] < ∞ then, (i) [K:F] < ∞, and (ii) [K:F] =[K:E][E:F]

Proof:

Let [K:E] = m and [E:F] = n, and consider the basis of K over E be {v₁, v₂, ···, v_m}, and the basis of E over F be {w₁, v₂, ···, w_n}.

∀u ∈K, then u = $\sum_{i=1}^m a_iv_i, ~a_i~∈~E$ because K is a vector space over E with basis {v₁, v₂, ···, v_m}, and E is a vector space over F with basis {w₁, v₂, ···, w_n}, so a_i ∈ E, then $a_i=\sum_{j=1}^n b_{ij}w_j, b_{ij}∈F$

u = $\sum_{i=1}^m a_iv_i=\sum_{i=1}^m\sum_{j=1}^n b_{ij}(v_iw_j),b_{ij}∈F$

And therefore, the set {v_iw_j} where i=1,···, m and j=1, ···, n form a set generator with nm elements of the vector space K over F, so [K:F] ≤ mn, and therefore [K:F] < ∞ (i).

To prove the set {v_iw_j} forms a basis, we need to show these vectors are linearly independent.

Assume $\sum_{i=1}^m\sum_{j=1}^n b_{ij}(v_iw_j)=0, b_{ij}∈F$. We need to prove that b_ij = 0. This sum can be rewritten as $\sum_{i=1}^m\sum_{j=1}^n (b_{ij}w_j)v_i=0$ [Commutativity and Associativity] and $\sum_{i=1}^m c_iv_i=0, where~ c_i=\sum_{j=1}^n (b_{ij}w_j)∈E$ is a linear combination of vectors of E with scalars of F.

As {v₁, v₂, ···, v_m} is a basis of K over E ⇒ c_i = 0, i = 1, 2, ···, m ⇒ $c_i=\sum_{j=1}^n (b_{ij}w_j)=0$ where b_ij ∈ F and {w₁, v₂, ···, w_n} is a basis of E over F ⇒ b_ij = 0 ∎ Therefore, (ii) [K:F] = n·m = [K:E]·[E:F]

Exercise. Show that $\sqrt{2}∉ℚ(\sqrt[5]{2})$. The irreducible polynomial of $\sqrt[5]{2}$ is x⁵ - 2 ∈ ℚ[x] (Eisenstein criteria, p = 2) ⇒[x⁵ - 2 irr. ⇒ ⟨x⁵-2⟩ maximal ⇒ ℚ($\sqrt[5]{2}) = \frac{ℚ[x]}{⟨x^5-2⟩}$] [ℚ($\sqrt[5]{2}$) : ℚ] = 5. For the sake of contradiction suppose $\sqrt{2}∈ℚ(\sqrt[5]{2})$, then there is a tower of extensions $ℚ ⊆ ℚ(\sqrt{2}) ⊆ ℚ(\sqrt[5]{2})$ ⇒ [ℚ($\sqrt[5]{2}$) : ℚ] = 5 = [ℚ($\sqrt[5]{2}$) : ℚ($\sqrt{2}$)] · [ℚ($\sqrt{2}$) : ℚ] = α · 2, α ∈ ℕ ⊥. Observe that [ℚ($\sqrt{2}$) : ℚ] = 2, x² -2 is an irreducible polynomial of ℚ with root $\sqrt{2}$.

Definition. An embedding of F into E is an injecting homomorphism of a field F into a field E, σ: F → E.

Theorem. Let E and F be two fields, and let σ: F → E be an embedding of a field F into a field E. Then there exist a field K such that F is a subfield of K and σ can be extended to an isomorphism of K onto E.

Notice that (i) K is an extension of F. (ii) σ can be extended to σ*: K → E, and σ* is an isomorphism of K onto E (Figure 1.e.).

Proof.

Notice that σ: F → E is an embedding ⇒ σ is homomorphism, 1-1, σ(F)⊂E (it is not onto). We are going to define a new set S such that cardinality(S) = cardinality(E -σ(F)), and S ∩ F = ∅. Then, let f: S → E -σ(F) be a bijection (1-1 and onto), and let K = F ∪ S.

Define σ*: K → E, σ*(a)$ = \begin{cases} σ(a), &a ∈ F\\\\ f(a), &a ∈ S \end{cases}$

We claim that σ* is an isomorphism of K onto E.

1. It is well-defined. If a ∈ F, a is “landing” on E because σ is an embedding of a field F into E. If a ∈ S, a goes to E - σ(F) ⊆ E.
2. σ* is one-to-one, i.e., σ*(a) = σ*(b) ⇒ a = b. If a, b ∈ F, σ*(a) = σ*(b) ⇒ σ(a) = σ(b) ⇒ [σ is one-to-one] a = b. If a, b ∈ S, σ*(a) = σ*(b) ⇒ f(a) = f(b) ⇒ [f is bijection] a = b. Notice that S ∩ F = ∅, so σ*(a) = σ*(b) ⇒ a, b ∈ S or a, b ∈ F.
3. σ* is onto. Notice that E is composed of σ(F) and E - σ(F). Every element of σ(F) has a pre-image element because σ(F) is obviously onto, and every element of E - σ(F) has a pre-image element because f is bijective.
4. σ* is homomorphism. It is left to the reader to prove it, but considering that,

We have defined K = F ∪ S. The field structure on K is defined ∀x, y ∈ K, as

• x⊕y = (σ*)^-1(σ*(x) + σ*(y))
• x⊙y = (σ*)^-1(σ*(x) σ*(y))

Therefore, if σ: F → E is an embedding, we can identify F with the corresponding image σ(F) in E, basically we write 'x' in place of σ(x). Futhermore, E (E ≋ K), hence it can be considered as an extension of F.

Theorem. Let p(x) be an irreducible polynomial in F[x]. Then, there exists an extension E of F in which p(x) has a root.

Proof. Suppose p(x) is an irreducible polynomial in F[x] ⇒ The ideal generated by p(x), i.e., ⟨p(x)⟩ is a maximal ideal ⇒ E = F[x]/⟨p(x)⟩ is a field.

Define σ: F → E by σ(a) = $\bar a=a+⟨p(x)⟩$ It is easy to prove that σ is one-to-one and homomorphism, so σ is an embedding of F into E. Using the previous result, E is regarded as an extension of F.

Let p(x) = a₀ + a₁x + ··· + a_nxⁿ, be a polynomial in F[x], a_n ≠ 0, a_i ∈ F

Then, in E, x + ⟨p(x)⟩ is a zero or root of p. $p(x + ⟨p(x)⟩)=a_0 + a_1(x + ⟨p(x)⟩) + ··· + a_n(x + ⟨p(x)⟩)^n=$ a₀ + a₁x + ⟨p(x)⟩ + a₂x² + ⟨p(x)⟩ ··· + a_nxⁿ + ⟨p(x)⟩ = p(x) + ⟨p(x)⟩ =[By absorption] 0 + ⟨p(x)⟩.

Krnoecker’s Theorem. Existence of extension. Let F be a field and let f(x) be a non-constant polynomial in F[x]. Then, there exists an extension E of F in which f(x) has a root or zero. (Figure 1.f)

Proof.

There are two cases:

1. Case I. f(x) ∈ F[x] has a root in F. Thus, we can say, there exists an extension F of F, the trivial extension, in which f(x) has a root.
2. Case II. Let f(x) ∈ F[x] does not have a root in F.

Every field F is a UFD (every non-zero non-unit element can be written as a product of prime or irreducible elements, uniquely up to order and units) because it is an integral domain and everything non-zero is a unit. The polynomial ring over F is a UFD, that is, F[x] is a UFD, too, and therefore f(x) can be factored into the product of irreducible polynomials. Let p(x) be an irreducible factor of f(x) in F[x].

Let p(x) be an irreducible polynomial in F[x] ⇒ We know that the ideal generated by any irreducible polynomial is a maximal ideal, ⟨p(x)⟩ is a maximal ideal. Moreover, the quotient ring E = F[x]/⟨p(x)⟩ is a field.

Let’s define σ: F → E by σ(a) = $\overline a$ = a + ⟨p(x)⟩. σ is a one-to-one homomorphism, and therefore E has a subfield isomorphic to F. It is reasonable to think of E as containing F and identify the coset a + ⟨p(x)⟩ with its coset representative that belongs to F as just “a” and vice versa or, in other words, σ is an embedding of F into E.

Finally, let’s prove that p(x) = a₀ + a₁x + ··· + a_nxⁿ has a root in E, where a_i ∈ F, a_n ≠ 0

Then, in E, x + ⟨p(x)⟩ is a zero or root of p. p(x + ⟨p(x)⟩) = a₀ + a₁(x + ⟨p(x⟩) + a₂(x + ⟨p(x⟩)² + ··· + a_n(x + ⟨p(x⟩)ⁿ = a₀ + a₁(x + ⟨p(x⟩) + ··· + a_n(xⁿ + ⟨p(x⟩) = p(x) + ⟨p(x⟩) = 0 + ⟨p(x⟩)∎

Theorem. Let p(x) be an irreducible polynomial in F[x] and let u be a root of p(x) in an extension E of F. Then,

1. F(u), the subfield of E generated by F and u is the smallest field containing F and u. It is indeed F[u], the smallest subring containing both F and u = {b₀ + b₁u + ··· + b_mu^m ∈ E | b₀ + b₁x + ··· + b_mx^m ∈ F[x]}

2. If the degree of p(x) is n, the set {1, u, ···, u^n-1} forms a basis of F(u) over F, i.e., each element of F(u) can be written uniquely as c₀ + c₁u + ··· + c_nu^n-1 where c_i ∈ F, and [F(u):F] = n.

Example. Let p(x) = x² -2 be an irreducible polynomial in ℚ[x], x = $\sqrt{2}$ is its root in some extension E of ℚ. This theorem says,

(i) ℚ($\sqrt{2}$) is a subfield of E generated by ℚ and $\sqrt{2}$.

(ii) The set {1, $\sqrt{2}$} is the basis set of ℚ($\sqrt{2}$) because degree(x² -2 ) = 2. Moreover, every element in ℚ($\sqrt{2}$) can be uniquely represented as linear combination of 1 and $\sqrt{2}$, and [ℚ($\sqrt{2}$):ℚ] = 2.

Proof:

Let p(x) be any irreducible polynomial in F[x], and let u be a root of p(x) in an extension E of E.

(i) Let F(u) denote the smallest subfield of E containing F and u. F[u] = {b₀ + b₁u + ··· + b_mu^m ∈ E, where b₀ + b₁x + ··· + b_mx^m ∈ F[x]}

We claim that F[u] = F(u). Consider the map Φ:F[x] → E, defined as Φ(b₀ + b₁x + ··· + b_mx^m) = b₀ + b₁u + ··· + b_mu^m where b₀ + b₁x + ··· + b_mx^m ∈ F[x].

We claim that Φ is a homomorphism.

Φ ( (b₀ + b₁x + ··· + b_mx^m) + (c₀ + c₁x + ··· + c_mx^m) ) = Φ ((b₀+c₀) + (b₁+c₁)x + ··· + (b_m+c_m)x^m) = (b₀+c₀) + (b₁+c₁)u + ··· + (b_m+c_m)u^m = (b₀ + b₁u + ··· + b_mu^m) + (c₀ + c₁u + ··· + c_mu^m) = Φ(b₀ + b₁x + ··· + b_mx^m) + Φ(c₀ + c₁x + ··· + c_mx^m)

Analogously, Φ ( (b₀ + b₁x + ··· + b_mx^m) · (c₀ + c₁x + ··· + c_mx^m) ) = Φ ((b₀c₀) + (b₀c₁+b₁c₀)x + ··· + (b_mc_m)x^2m) = (b₀c₀) + (b₀c₁+b₁c₀)u + ··· + (b_mc_m)u^2m) = (b₀ + b₁u + ··· + b_mu^m) · (c₀ + c₁u + ··· + c_mu^m) = Φ(b₀ + b₁x + ··· + b_mx^m) · Φ(c₀ + c₁x + ··· + c_mx^m)

ker(Φ) contains all those polynomials f(x) such that Φ(f(x)) = 0, i.e., f(u) = 0. By assumption u is a root of p(x), p(x) ∈ Ker(Φ).

As F[x] is a polynomial ring and a principal ideal domain (PID). Thus, since Ker(Φ) is an ideal, it is generated by a single element, say Ker(Φ) = ⟨g(x)⟩ ⇒[p(x) ∈ Ker(Φ)] p(x) = g(x)·h(x) for some h(x) ∈ F[x]. However, because p(x) is irreducible, h(x) is a scalar (h(x) ∈ F)

∴ ⟨g(x)⟩ = ⟨p(x)⟩ = Ker(Φ).

Using the Fundamental Theorem of Homomorphism, Image(Φ) ≋ F[x]/Ker(Φ) ↭ {b₀ + b₁u + ··· + b_mu^m ∈ E, where b₀ + b₁x + ··· + b_mx^m ∈ F[x]} ≋ F[x]/Ker(Φ) ↭ F[u] ≋ F[x]/Ker(Φ) = F[x]/⟨p(x)⟩. Remember that p(x) is irreducible in F[x] ↭ the ideal generated by this polynomial ⟨p(x)⟩ is maximal and F[x]/⟨p(x)⟩ is a field. Moreover, it is the smallest subfield of E containing F and u. Thus, F[u] = F(u).

(ii) Consider the elements 1, u, u², ···, u^n-1 in F(u) and let p(x) be any minimal or irreducible polynomial of u over F of degree n.

Let’s suppose by reduction to the absurd that {1, u, u², ···, u^n-1} is linearly dependent. Let α₀·1 + α₁·u + ··· + α_n-1·u^n-1 = 0, where α_i ∈ F and not all α_i’s are zero ⇒ u satisfies a polynomial of degree n-1 < degree(p(x)), and we have assumed that p(x) is the minimal (or irreducible) polynomial of u over F ⊥ ⇒ {1, u, u², ···, u^n-1} is linearly independent.

Next, we need to prove that {1, u, u², ···, u^n-1} is the generating set of F(u). Let f(u) ∈ F(u) ⇒[Recall F[u] = {b₀ + b₁u + ··· + b_mu^m ∈ E, where b₀ + b₁x + ··· + b_mx^m ∈ F[x]}≋ F[x]/Ker(Φ) ≋ F[x]/⟨p(x)⟩ ≋ F(u) ] f(x) ∈ F[x] and p(x) ∈ F[x] ⇒ [By the division algorithm] f(x) = p(x)q(x) + r(x) where r(x) = 0 or deg(r(x)) < deg(p(x)) ⇒ f(u) = p(u)q(u) + r(u) ⇒ [u is a root of p(x)] f(u) = r(u) 🚀.

As deg(r(x)) < deg(p(x)) = n ⇒ deg(r(x)) < n. r(x) = β₀ + β₁x + ··· + β_n-1x^n-1 is a polynomial of F[x] of degree n-1

∴ f(u) =🚀 r(u) = β₀ + β₁u + ··· + β_n-1u^n-1. Hence, for any arbitrary f(u) ∈ F(u) is generated from {1, u, u², ···, u^n-1}. Thus, {1, u, u², ···, u^n-1} is a basis of F(u) over F and this set has n-elements, so [F(u):F] = n∎

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.