The Field of Quotients and More Exercises

“Don’t patronize me. My face makes onions and blind kids cry, vultures vomit, grannies ran past me, ghosts shiver, Medusa turn to stone, and the mother of all assholes very proud,” Apocalypse, Anawim, #justtothepoint.

Recall that a field is a commutative ring with unity such that each nonzero element has a multiplicative inverse, e.g., every finite integral domain, ℤ_p (p prime), ℚ, ℝ, and ℂ. A field has characteristic zero or characteristic p with p prime.

(ℤ, +, ·) is an integral domain, but not a field. However, we can construct a field containing the quotients of elements of ℤ, e.g. {a/b | a, b ∈ ℤ, a ≠ 0} = ℚ, where there is an equivalent relation defined by a/b = c/d whenever ad = bc, and we know that (ℚ, +, ·) is a field. Let’s try to generalize this idea.

Theorem. Let D be an integral domain, that is, a commutative ring with unity having no divisors of zero. Then, there exists a field F (that is called the field of quotients of D) that contains a subring isomorphic to D. In other words, the integral domain is enlarged to a field such that every element of F can be expressed as a quotient of two elements of D.

Proof.

• 1st Step. Define what the elements of F are.

Consider D x D = {(a, b) | a, b ∈ D}

Example, D = ℤ, (2, 3) ∈ ℤ x ℤ, the idea is 2/3. However, we need to be cautious, 2/0 is not defined and 2/4 = 1/2.

S = {(a, b) | a, b ∈ D and b ≠ 0}. Two elements (a, b) and (c, d) in S are equivalent, denoted by (a, b) ~ (c, d), if and only if ad = bc. Figure 1.a  

1. Reflexivity. (a, b) ~ (a, b) since ab = ba because a, b are elements of D. D is an integral domain, so it is a commutative ring.
2. Symmetric. Let (a, b) ~ (c, d) ⇒ ad = bc ⇒ [a, b, c, d ∈ D, and D is an integral domain, multiplication is commutative] da = cb ⇒ (c, d) ~ (a, b)
3. Transitive. Let (a, b) ~ (c, d) and (c, d) ~ (r, s) ⇒ ad = bc and cs = dr.

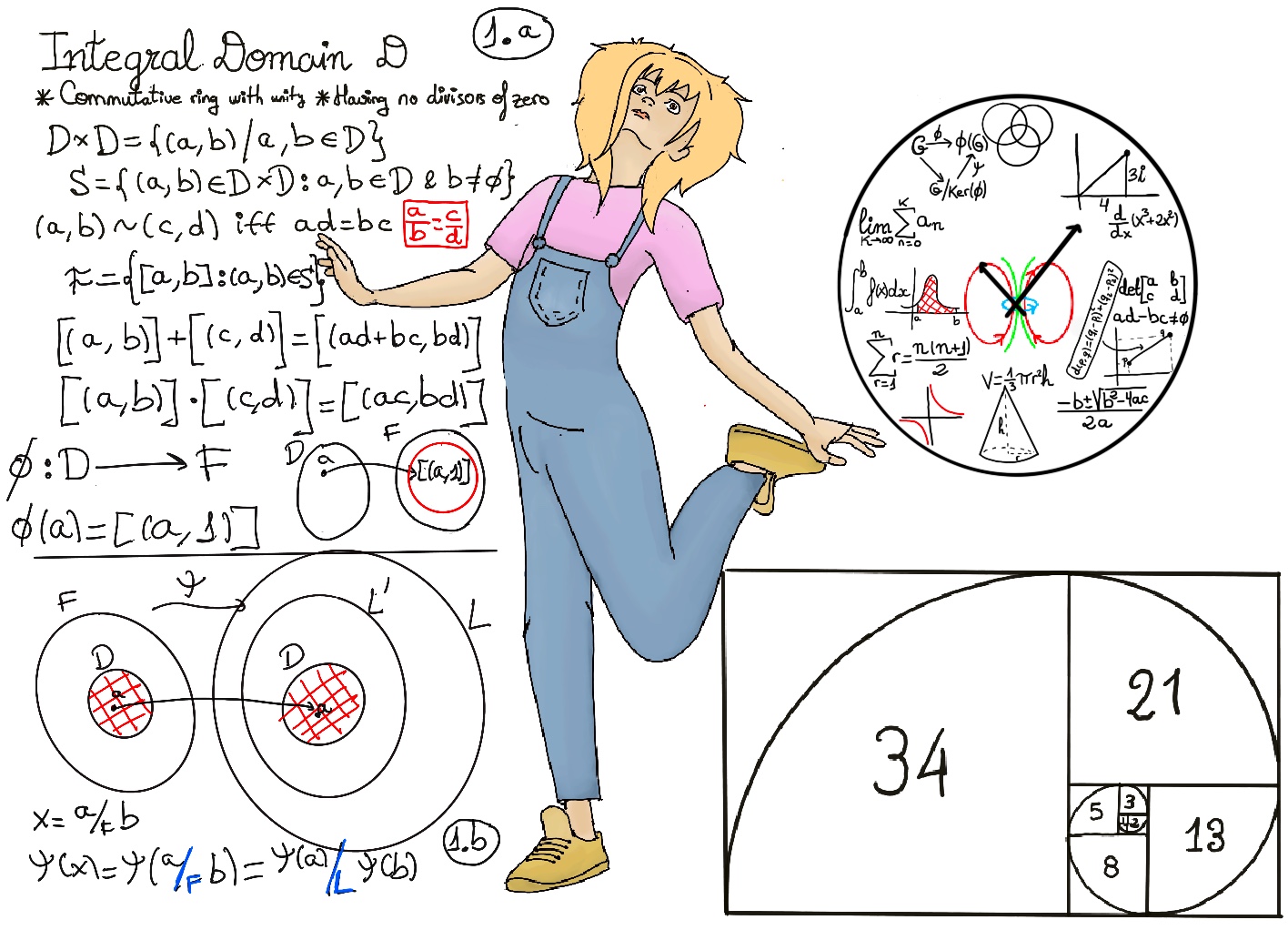
(a, b ) ~ (r, s) ↭ as = br ?

asd = [D integral domain, commutative ring] s(ad) = [(a, b) ~ (c, d) ⇒ ad = bc] sbc = bcs = [(c, d) ~ (r, s) ⇒ cs = dr] bdr = brd

In short, asd = brd ⇒ [D integral domain, it has not divisors of zero ⇒ the left cancellation law applies] as = br ⇒ (a, b ) ~ (r, s).

This equivalent relation partitions the set S into disjoint equivalent classes. Let F be the set of such equivalent classes, F = {[(a, b)]: (a, b) ∈ S}

[1/2] = {1/2, 2/4, 3/6,···} where 1/2 = 2/4 ↭ 1·4 = 2·2

• 2nd Step. We need to define the binary operations of addition and multiplication on F.

1. [(a, b)] + [(c, d)] = [(ad + bc, bd)]
2. [(a, b)] · [(c, d)] = [(ac, bd)]

Let’s prove that they are well defined, i.e., they do not depend on the choices of representatives. ∀(a₁, b₁) ∈ [(a, b)], ∀(c₁, d₁) ∈ [(c, d)] ⇒ a₁b = b₁a, c₁d = d₁c

We claim that [(a₁d₁ + b₁c₁, b₁d₁)] = [(ad + bc, bd)] ↭ (a₁d₁+b₁c₁)bd = b₁d₁(ad + bc)

a₁b = b₁a ⇒ [Multiplying by d₁d both sides of the equation] a₁bd₁d = b₁ad₁d (i)

c₁d = d₁c ⇒ [Multiplying by b₁b both sides of the equation] c₁db₁b = d₁cb₁b (ii)

(i) + (ii) = a₁bd₁d + c₁db₁b = b₁ad₁d + d₁cb₁b ⇒ (a₁d₁+b₁c₁)bd = b₁d₁(ad + bc) ⇒ (a₁d₁ + b₁c₁, b₁d₁) ~ (ad + bc, bd) ⇒ (a₁d₁ + b₁c₁, b₁d₁) ∈ [(ad + bc, bd)] or [(a₁d₁ + b₁c₁, b₁d₁)] = [(ad + bc, bd)]

Analogously, we claim (a₁c₁, b₁d₁) ∈ [(ac, bd)]

a₁b = b₁a ⇒ a₁bc₁d = b₁ac₁d ⇒[c₁d = d₁c] a₁c₁bd = b₁d₁ac ⇒ (a₁c₁, b₁d₁) ~ (ac, bd) ⇒ (a₁c₁, b₁d₁) ∈ [(ac, bd)] ↭ [(a₁c₁, b₁d₁)] = [(ac, bd)]

• 3rd Step. Check all the fields axioms to show that F is indeed a field under these operations.

We need to demonstrate that (F, +) is an Abelian group, that is, + is a binary operation in F, associative, it does have an additive identity element, F contains additive inverses of all its elements, and commutative. Besides, (F - {0}, ·) is an Abelian group, that is, · is a binary operation in F, associative, exists a unity in F, all non-zero elements of F are units (multiplicative inverse), and commutative.

1. +, · are well-defined. [(a, b)] + [(c, d)] = [(ad + bc, bd)] and [(a, b)] · [(c, d)] = [(ac, bd)]

   We know that ∀a, b, c, d ∈ D ⇒ ad + bc, bd, ad, bd ∈ D. (a, b) and (c, d) ∈ S, b ≠ 0 and d ≠ 0 ⇒ [D is an integral domain ⇒ it does no have divisors of zero] bd ≠ 0

   [(a, b)] + [(c, d)] = [(ad + bc, bd)] ∈ F and [(a, b)] · [(c, d)] = [(ac, bd)] ∈ F and we have previously demonstrated that they do not depend on the choices of representatives.

2. +, · are associative, e,g, let’s prove that + is associative.

   [(a, b)] + { [(c, d)] + [(e, f)] } = [(a, b)] + [(cf + de, df)] =[D is an integral domain ⇒ Associative and Distributivity] [(adf + bcf + bde, bdf)]

   { [(a, b)] + [(c, d)]} + [(e, f)] = [(ad + bc, bd)] + [(e, f)] =[D is an integral domain ⇒ Associative and Distributivity] [(adf + bcf + bde, bdf)]

3. Identity elements -+, · respectively-: [(0, 1)], [(1, 1)] ∈ F.

   [(a, b)] + [(0, 1)] = [(a·1 + b·0, b·1)] = [(a, b)] = [(0, 1)] + [(a, b)]

   [(a, b)] · [(1, 1)] = [(1, 1)] · [(a, b)] = [(a, b)]

4. Additive inverses.

   [(a, b)] + [(-a, b)] = [(ab + -ba, b²)] = [(0, b²)] = [(0, 1)] because (0, b²) ~ (0, 1), (-a, b) ∈ S because -a ∈ D (a ∈ D and D is an integral domain), b ≠ 0, hence [(-a, b)] ∈ F.

5. All non zero elements are units.

   Let [(a, b)] be a nonzero element in F. If a = 0, then [(a, b)] = [(0, 1)], that is, F’s additional identity.

   Therefore, a ≠ 0 and [(b, a)] ∈ F, this is our element multiplicative inverse.

   [(a, b)][(b, a)] =[ Since [(a, b)] ∈ F ⇒ b≠0, and by assumption a ≠ 0 ⇒ ab ≠ 0 because D is an integral domain, so it does no have divisors of zero] [(ab, ba)] = [(ab, ab)] = [(1, 1)] because (ab, ab) ~ (1, 1).

6. +, · are commutative, too. It is left as an easy exercise to the reader to prove it (it is based on (D, +, ·) multiplicative).

• 4th Step. Show that F can be viewed as containing D as an integral subdomain.

To show that F can be regarded as containing D. We will show that there is a ring isomorphism from D to a subring of F.

Let Φ: D → F, defined by Φ(a) = [(a, 1)]

1. Φ is homomorphism. Φ(a + b) = [(a + b, 1)]. Φ(a) + Φ(b) = [(a, 1)] + [(b, 1)] = [(a·1 + 1·b, 1·1)] = [(a + b, 1)].

   Φ(a · b) = [(a · b, 1)]. Φ(a) · Φ(b) = [(a, 1)] · [(b, 1)] = [(ab, 1)].

2. Φ is one-to-one. Let’s suppose Φ(a) = Φ(b) ⇒ [(a, 1)] = [(b, 1)] ⇒ (a, 1) ~ (b, 1) ⇒ a·1 = b·1 ⇒ a = b.

By the first isomorphism theorem for rings, the mapping Φ: D → F is a ring isomorphism from D to Φ(D) = F’, i.e., D ≋ Φ(D) = F', hence there exist a field F that contains a subring isomorphic to D (Φ(D)). Futhermore, any element of F can be expressed or written as a quotient of two elements of D.

Let [(a, b)] ∈ F, [(a, b)] = [(a, 1)][(1, b)] = [(a, 1)][(b, 1)]^-1 = [This is for notation’s sake or notation “sugar”] $\frac{[(a, 1)]}{[(b, 1)]}=\frac{Φ(a)}{Φ(b)}$ Therefore, we can write any element of F as a quotient of two elements of D.

Theorem. Let F be a field of quotients of D and let L be any field containing D (Figure 1.b.). Then, there exists a map ψ: F → L that gives an isomorphism of F with a subfield of L such that ψ(a) = a ∀a ∈ D.

Proof. Let’s define a map ψ: F → L, ψ(a) = a ∀a ∈ D.

Let x ∈ F, x = [We are using the previous result that elements of F can be rewritten as quotients of elements of D] a/_Fb where a, b ∈ D (Figure 1.b).

Define ψ(x) = ψ(a)/_Lψ(b) since a, b ∈ D, ψ(a), ψ(b) ∈ L. Therefore, ψ(a/_Fb) = ψ(a)/_Lψ(b).

Notice that x = a/_Fb where a, b ∈ D, b ≠ 0, ψ(b) = [b ∈ D, ψ(a) = a ∀a ∈ D] b ≠ 0 ⇒ ψ(a)/_Lψ(b) ∈ L

is it ψ well-defined? Let a/_Fb, c/_Fd ∈ F, such that a/_Fb = c/_Fd ⇒ ad = bc ⇒ ψ(ad) = ψ(bc) ⇒ [a, b, c, d ∈ D ⇒ ad, bc ∈ D] ad = bc ⇒ ψ(a)ψ(d) = ψ(b)ψ(c) ⇒ ψ(a)ψ(b)^-1 = ψ(c)ψ(d)^-1 ⇒[Notation sugar] ψ(a)/_Lψ(b) = ψ(c)/_Lψ(d) ⇒ ψ(a/_Fb) = ψ(c/_Fd)

is it homomorphism? Let x, y ∈ F, x = a/_Fb and y = c/_Fd where a, b, c, d ∈ D, b ≠ 0, d ≠ 0.

ψ(x+y) = ψ(a/_Fb + c/_Fd) = ψ((ad+bc)/_Fbd) = ψ(ad + bc)/_Lψ(bd) =[a, b, c, d ∈ D ⇒ ad + bc, bd ∈ D] (ad + bc)/_L(bd) 🚀

ψ(x) + ψ(y) = ψ(a)/_Lψ(b) + ψ(c)/_Lψ(d) = ψ(a)ψ(b)^-1 + ψ(c)ψ(d)^-1 =[Multiplying by the identity does not make any difference or does it? ψ(d)ψ(d)^-1 = 1, ψ(b)ψ(b)^-1 = 1] ψ(a)ψ(b)^-1ψ(d)ψ(d)^-1 + ψ(c)ψ(d)^-1ψ(b)ψ(b)^-1 = (ψ(a)ψ(d) + ψ(b)ψ(c))(ψ(d)^-1ψ(b)^-1) =[Sock- Shoe Property and · commutative] (ψ(a)ψ(d) + ψ(b)ψ(c))(ψ(b)ψ(d))^-1 =[Notation sugar] (ψ(a)ψ(d) + ψ(b)ψ(c))/_Lψ(b)ψ(d) = (ad + bc)/_L(bd) =[🚀] ψ(x+y).

Similarly, it is left to the reader to prove that ψ(x·y) = ψ(x)·ψ(y)

is it one to one? ψ(a/_Fb) = ψ(c/_Fd) ⇒ ψ(a)/_Lψ(b) = ψ(c)/_Lψ(d) ⇒ ψ(a)ψ(b)^-1 = ψ(c)ψ(d)^-1 ⇒ ψ(a)ψ(d) = ψ(b)ψ(c) ⇒ ad = bc ⇒ [ad = bc ⇒ add^-1 = bcd^-1 ⇒ a = bcd^-1 ⇒ b^-1a = b^-1bcd^-1 ⇒ ab^-1 = cd^-1 ] a/_Fb = c/_Fd. Then, by the first isomorphism theorem F ≋ ψ(F), say L’ (Figure 1.b), which is a subfield of L.

Examples

• If R is a field, then its field of fractions is R itself.
• The field of fractions of ℤ is ℚ. The field of fractions of 2ℤ is also ℚ.
• Let D = ℤ[x]. Since ℤ is an integral domain, so is ℤ[x]. Then, the field of quotients or fractions of ℤ[x] is the set of rational functions {f(x)/g(x) | f(x), g(x) ∈ ℤ[x], where g(x) is not the zero polynomial}, i.e., functions of the form f(x)/g(x) where f(x) and g(x) are polynomials with integer coefficients.

Notice that this field contains the field of fractions of ℤ, namely ℚ. However, it is interesting to point out that the field of fractions of ℚ[x] is the same as the field of fractions of ℤ[x].

• Let p be a prime ⇒ ℤ_p is a field ⇒ Frac(ℤ_p) = ℤ_p. Besides, ℤ_p(x) = {f(x)/g(x)| f(x), g(x) ∈ ℤ_p[x], g(x) ≠ 0} is an infinite field of characteristic p.

Exercises

• The set $ℚ[\sqrt{2}]$ = {a + b$\sqrt{2}$: a, b ∈ ℚ} is a field.

$ℚ[\sqrt{2}] ⊆ ℝ, ℚ[\sqrt{2}] ≠ ∅$. Let’s prove that ∀x, y ∈ $ℚ[\sqrt{2}], x -y ∈ ℚ[\sqrt{2}], xy ∈ ℚ[\sqrt{2}]$. Hence $ℚ[\sqrt{2}]$ is a subring of ℝ where we know that ℝ is a field.

$x = a +b\sqrt{2}, y =c +d\sqrt{2}$ where a, b, c, d ∈ ℚ, $x -y = (a -c) + (b -d)+\sqrt{2}∈ ℚ[\sqrt{2}], xy = (ac + 2bd) +(ad +bc)\sqrt{2} ∈ ℚ[\sqrt{2}]$

In (ℝ, ·), the multiplication is commutative ⇒ it is commutative in its subfield $ℚ[\sqrt{2}]$, so we have a commutative ring. Futhermore, 1 = 1 + 0$\sqrt{2}∈ ℚ[\sqrt{2}]$, hence it is a commutative ring with unity. ℝ has no zero divisors ⇒ $ℚ[\sqrt{2}]$ has no zero divisors, so $ℚ[\sqrt{2}]$ is a commutative ring with no zero divisors ⇒ $ℚ[\sqrt{2}]$ is an integral domain.

$(a+b\sqrt{2})(\frac{a}{a^2-2b^2}+\frac{-b}{a^2-2b^2}\sqrt{2}) = \frac{a^2}{a^2-2b^2} +\frac{-ab}{a^2-2b^2}\sqrt{2} + \frac{ba}{a^2-2b^2}\sqrt{2} - \frac{b^2}{a^2-2b^2}2 = \frac{a^2}{a^2-2b^2}- \frac{b^2}{a^2-2b^2}2 = 1$ ⇒ $(a+b\sqrt{2})^{-1}=\frac{a}{a^2-2b^2}+\frac{-b}{a^2-2b^2}\sqrt{2} ∈ ℚ[\sqrt{2}]$.

Note: if a, b ∈ ℚ, and at least one of a or b is not equal to zero ($a + b\sqrt{2} ≠ 0$), then a² -2b² ≠ 0. Suppose for the sake of contradiction, a² -2b² = 0 ⇒ a² = 2b² ⇒[if b = 0 ⇒ a² = 0 ⇒ a = b = 0 ⊥ at least one of a or b is not equal to zero] (a/b)² = 2 ⇒ $\sqrt{2} = \frac{a}{b} ∈ ℚ$ ⊥ Hence, $ℚ[\sqrt{2}]$ is a commutative division ring (inverses), that is, a field.

• Find all ring isomorphisms Φ: $\mathbb{Q[\sqrt{3}]→Q[\sqrt{3}]}$

First, let’s recall that Φ(1) = 1. ∀n ∈ ℕ, Φ(n) = Φ(1 + 1 + ··_n·· + 1) = Φ(1) + Φ(1) + ··_n·· +Φ(1) = n·Φ(1) = n·1 = n. Besides, 0 =[Φ preserves the additive identity] 0 = Φ(0) = Φ(n + (-n)) = Φ(n) + Φ(-n) = n + Φ(-n) ⇒ n + Φ(-n) = 0, and therefore Φ(-n) = -n, hence Φ(n) = n ∀n ∈ ℤ.

1 = Φ(1) = Φ(1/n + 1/n + ··_n·· + 1/n) = Φ(1/n) + Φ(1/n) + ··_n·· +Φ(1/n) = n·Φ(1/n), and therefore n·Φ(1/n) = 1 ⇒ Φ(1/n) = 1/n, ∀n ∈ ℕ.

∀m/n ∈ ℚ, Φ(m/n) = Φ(m·1/n) = Φ(m)·Φ(1/n) = m·1/n = m/n, hence ∀x ∈ ℚ, Φ(x) = x.

3 = Φ(3) = $Φ(\sqrt{3}\sqrt{3}) = Φ(\sqrt{3})Φ(\sqrt{3}) = Φ(\sqrt{3})^2⇒Φ(\sqrt{3}) = ±\sqrt{3}$. Then, ∀ $x ∈ℚ[\sqrt{3}], x = a + b\sqrt{3}, Φ(a + b\sqrt{3}) = a ± b\sqrt{3}$

All that is left to prove that the identity and $Φ(a + b\sqrt{3}) = a - b\sqrt{3}$ are indeed ring isomorphisms and it is left as an easy exercise.

• The quadratic fields $\mathbb{Q[\sqrt{2}]}$ and $\mathbb{Q[\sqrt{3}]}$ are not isomorphic.

For the sake of contradiction, let’s assume that there is an isomorphism Φ: $\mathbb{Q[\sqrt{2}]}→\mathbb{Q[\sqrt{3}]}$. By the similar reasoning as the previous problem, Φ(x) = x ∀x ∈ ℚ.

Let $Φ(\sqrt{2}) = a + b\sqrt{3} ∈ ℚ[\sqrt{3}]$ where a, b ∈ ℚ.

2 =[Φ(x) = x ∀x ∈ ℚ] Φ(2) = $Φ(\sqrt{2}\sqrt{2}) = Φ(\sqrt{2})^{2} = (a + b\sqrt{3})^{2} = 2 ⇒ a^2 +3b^2 +2ab\sqrt{3} = 2$ ⇒ [Suppose ab ≠ 0] $\sqrt{3} = \frac{2 -a^2 -3b^2}{2ab} ∈ \mathbb{Q}$ ⊥. If ab = 0 ⇒ a = 0 or b = 0. If a = 0, then 2 = 3b² ⇒ $b = ±\sqrt{\frac{2}{3}}∉ℚ$ ⊥ If b = 0 ⇒ 2 = a² ⇒ $a = ±\sqrt{2}∉ℚ$ ⊥

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.