
|
 |
 |
|
 |
Do one thing every day that scares you, Eleanor Roosevelt.
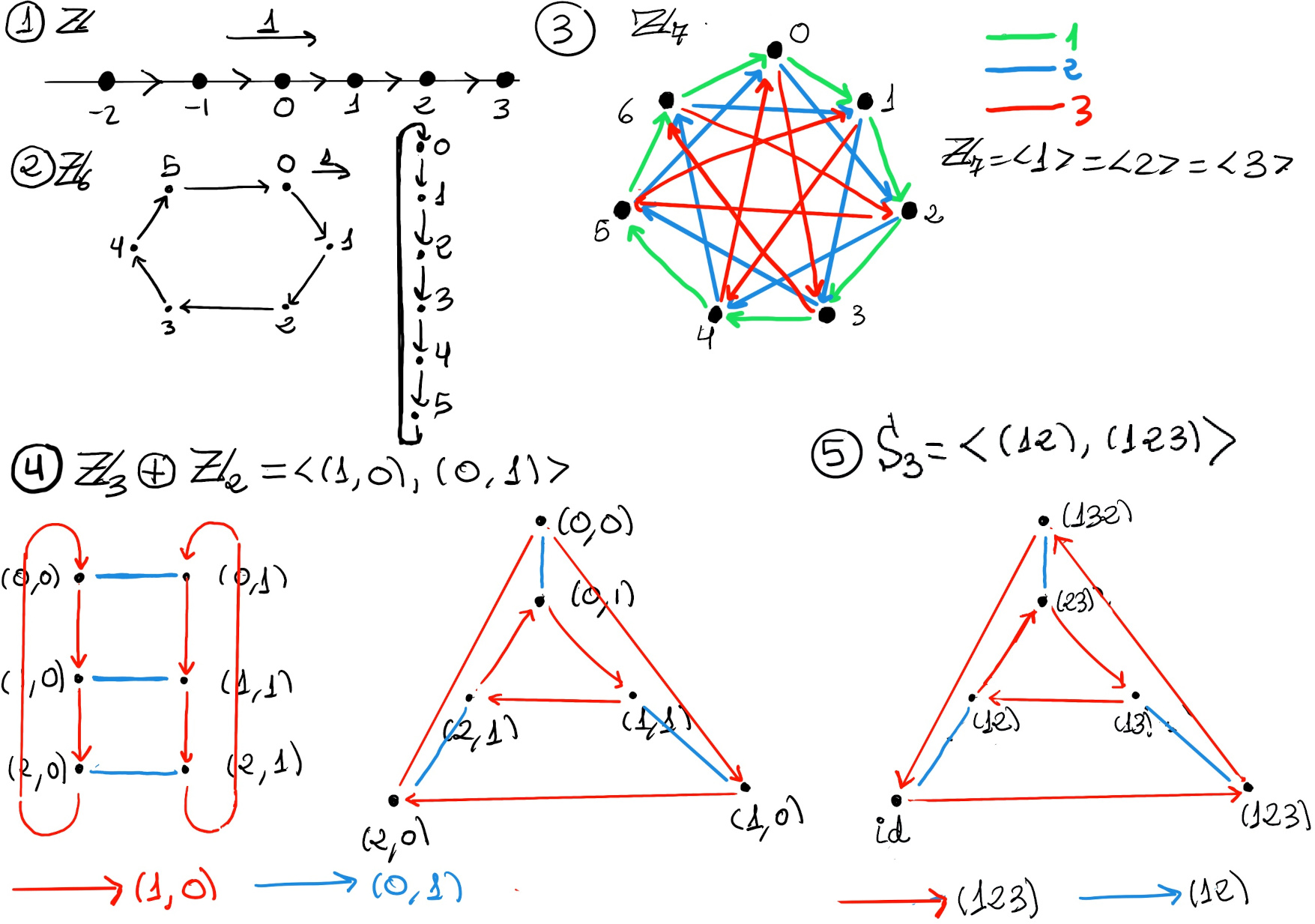
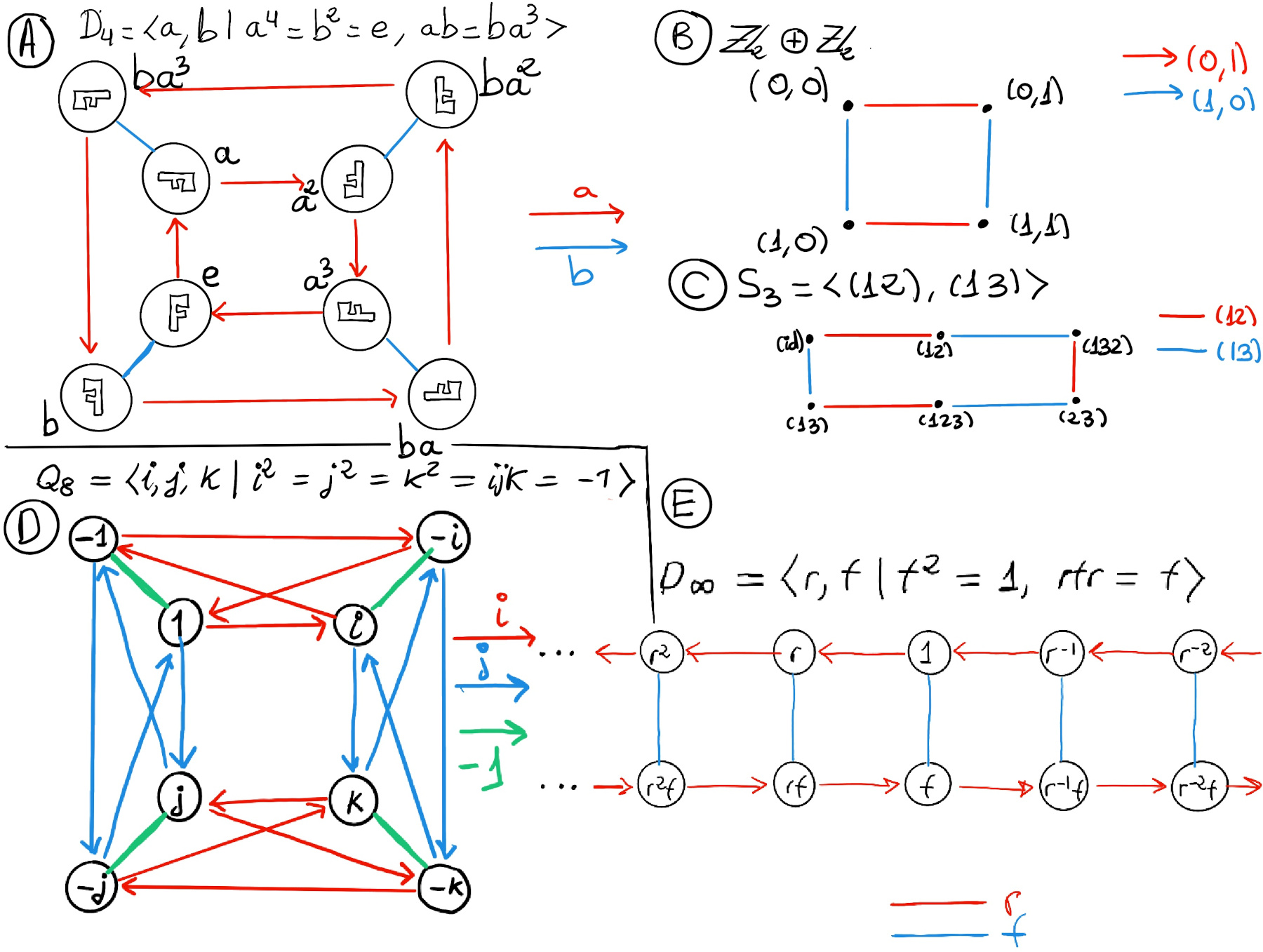
A presentation is one method of specifying a group. It comprises a set of generators S (elements that we want to generate the group) and a set of relations or equations R among those generators, we then say G has presentation ⟨S | R⟩, e.g., D4 = ⟨r, f | r4 = f2 = (rf)2 = id⟩, ℤ x ℤ = ⟨a, b | ab = ba⟩, ℤ4⊕ ℤ2 = ⟨a, b | a4 = b2 = e and ab = ba⟩
A graph, G, is a pair (V, E) where V is a set and E is a set of 2-element subsets of V . The set V is almost always finite and its elements are called vertices.
Definition. Let G be a group and S be a generating set of G. The Cayley graph, written as τ(G, S) or Cay(S:G), is an edge-colored (it assigns a color to each edge) directed graph (a graph that is made up of a set of vertices connected by directed edges called arcs) constructed as follows:
It provides a way to visualizing a group. They clearly communicate the group’s structure and complexity (or lack thereof).

Facts:
A Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once without returning to the starting point. A Hamiltonian cycle (or Hamiltonian circuit) is a cycle that visits each vertex exactly once.
There can be more than one Hamiltonian path in a single graph but the graph must be connected to have the possibility of the existence of a Hamiltonian path.
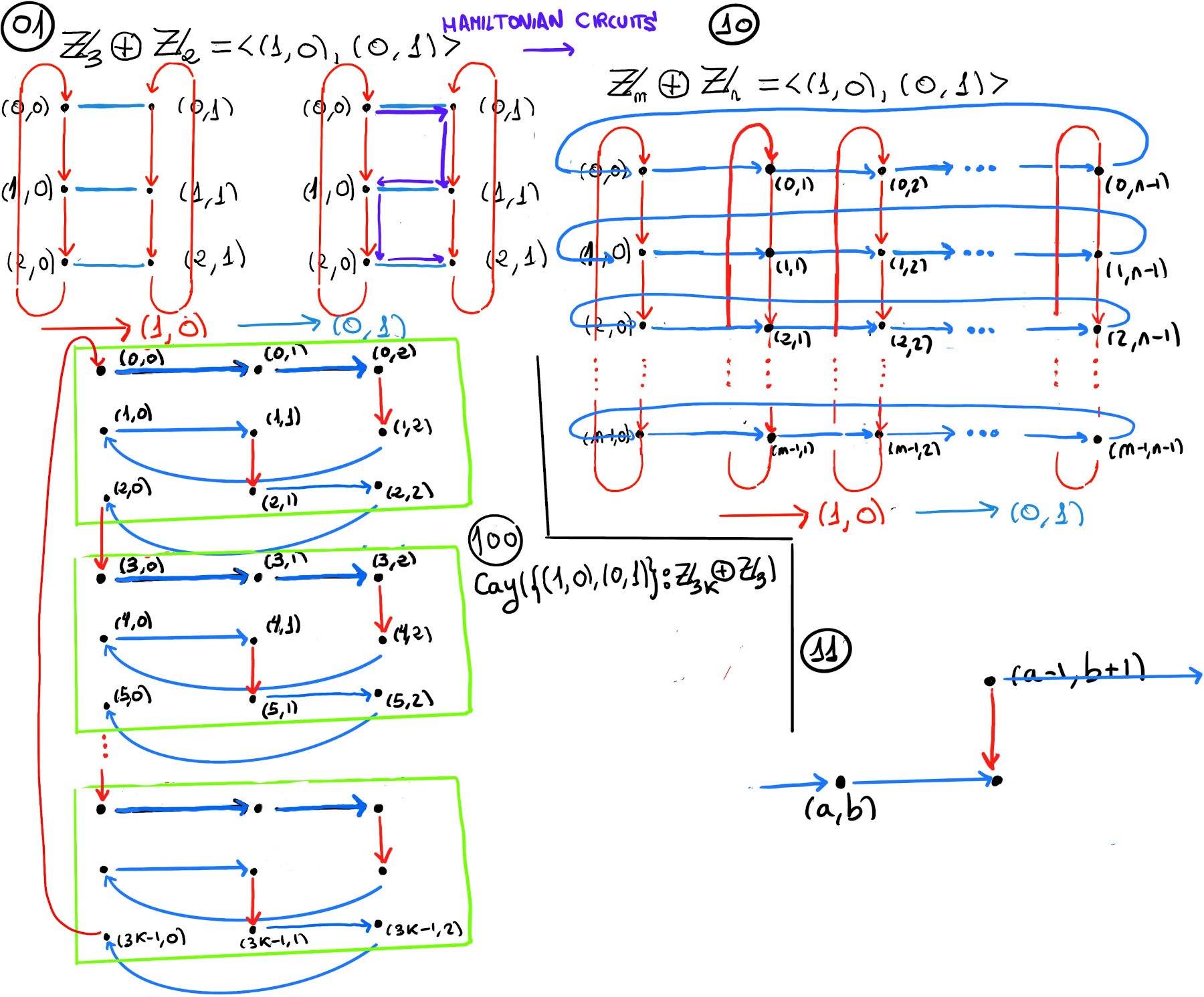
We want to research the existence of Hamiltonian circuits in Cay({(1, 0), (0, 1): ℤm⊕ℤn}) where m, n > 1 and gcd(m, n) = 1 (Figure 100).
If there is a Hamiltonian circuit and (a, b) is a vertex from which the circuit exists horizontally, then, it immediately follows, the circuit must exist (a -1, b +1) horizontally, too because otherwise the circuit would pass through (a, b + 1) twice (Figure 11). Then, repeating this argument, the circuit exists horizontally from each of the vertices (a, b), (a-1, b +1)(a -2, b +2),….that is, the coset (a, b) + ⟨(-1, 1)⟩. Futhermore, gcd(m, n) = 1 ⇒ ⟨(-1, 1)⟩ = ℤm⊕ℤn (that is, (-1, 1) generates the entire group). However, this is a contradiction because there cannot be a Hamiltonian circuit consisting entirely and exclusively of horizontal moves.

Theorem. Cay({(1, 0), (0, 1): ℤm⊕ℤn}) does not have a Hamiltonian circuitwhen m, n > 1 and gcd(m, n) = 1.
Theorem. Cay({(1, 0), (0, 1): ℤm⊕ℤn}) has a Hamiltonian circuit when n divides m.
Proof.
n divides m ⇒ ∃k ∈ ℤ: m = kn, then we may think of ℤm⊕ℤn as k blocks of size n x n (Figure 100). The Hamiltonian circuit is given as follows,
Let k ∈ ℤ, k * (a, b, c, ···) denotes the concatenation of k copies of the sequence (a, b, c, ···). Thus, this proof can be expressed as m * [(n - 1) * (0, 1), (1, 0)]
Theorem. Let G be a finite Abelian group and S any non-empty generating set for G. Then, the Cayley diagraph of G, Cay(S:G), has a Hamiltonian path.
Proof.
Let’s induct on the order of the generating set for G, |S|.
Base case. |S|=1, that is, S = ⟨a⟩, then the digraph is just a circle labeled with e → a → a2 →···→ am-1, where |a| = m, and there is an obvious Hamiltonian path for this Cayley diagraph.
Let’s |S| > 1, S = {s1, s2, …, sn-1, sn} and pick some arbitrary element s. Without losing any generality, let’s take the last element, sn = s ∈ S, and define T = S - {s}, H = ⟨s1, s2, …, sn-1⟩
|T| < |S| and H is a finite Abelian group ⇒ [By the induction hypothesis] ∃(a1, a2,···, ak) a Hamiltonian path in Cay(T:H)
We claim that (a1, a2,···, ak, s, a1, a2,···, ak, a1, a2,···, ak, s, a1, a2,···, ak, a1, a2,···, ak, s, a1, a2,···, ak, a1, a2,···, ak) where a1, a2,···, ak occurs |G|/|H| times and s appears |G|/|H| -1 times is indeed a Hamiltonian path.
By assumption S generates G, T = S - {s}, s = sn, H = ⟨s1, s2, …, sn-1⟩ ⇒[If group G is Abelian and H ≤ G, the quotient group G/H is a group] the coset Hs generates the factor group G/H. Thus, the cosets of H are H, Hs, Hs2,…, Hsn where n = |G|/|H| - 1.