Conjugacy Classes. The Class Equation.

1st Law. Males are fucked when getting married, there is nothing fair and equal about the divorce. You’re a man, you’re going to get bent over and you’re going to take it dry. Besides, the “so called Catholic church” will look another way and stay in communion with your ex, but if you get married or live together with someone else you are an adulterous, hence go to hell and be tormented forever and ever, Apocalypse, Anawim, #justtothepoint.

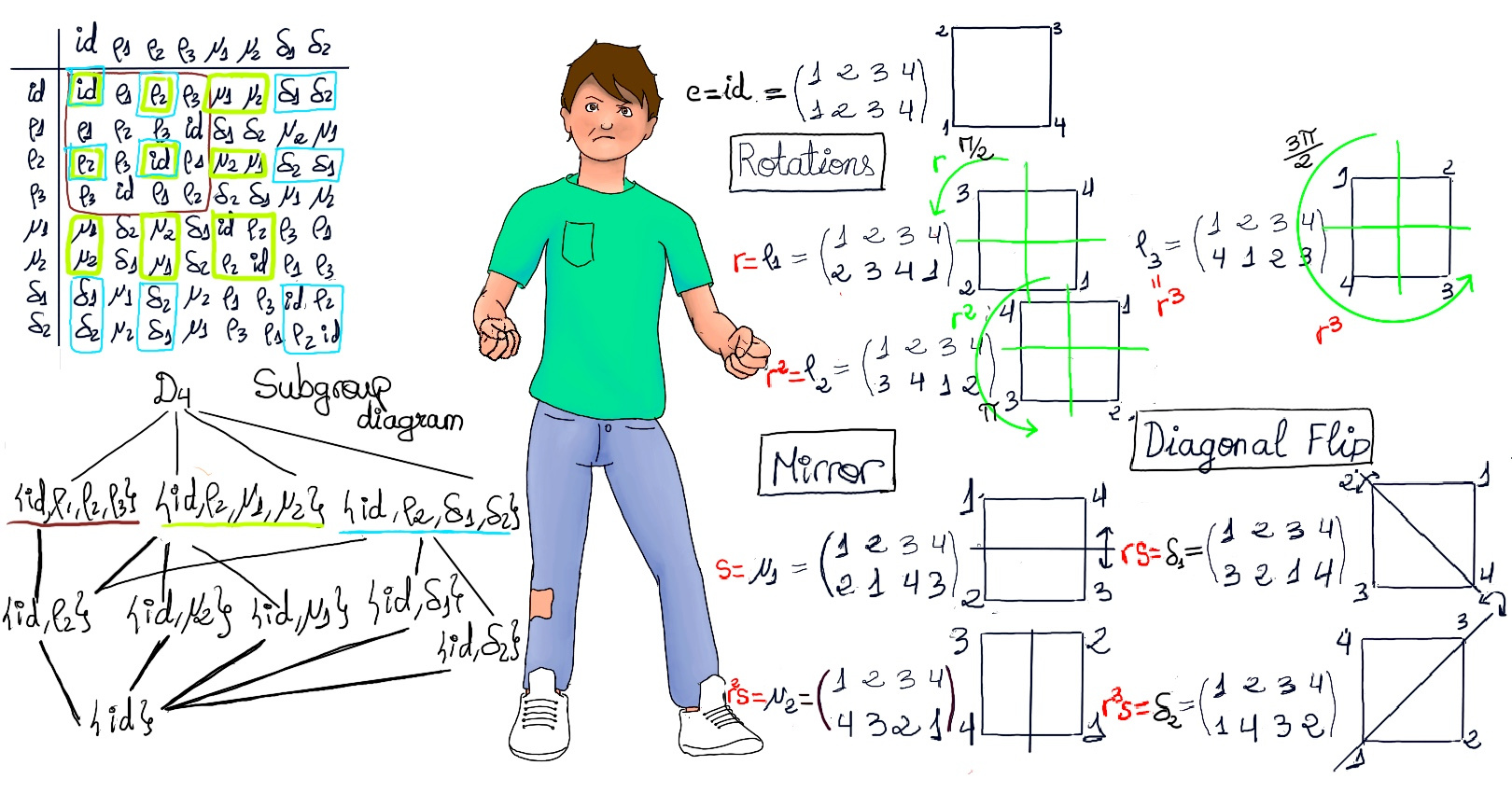
Definition. Any two elements a and b of a group G are said conjugate if xax^-1 = b for some x ∈ G.

Conjugacy is an equivalent relation on G, and the conjugacy class of “a”, denoted by cl(a) ={xax^-1 | x ∈ G} is the equivalence class of “a” under conjugacy, and therefore we could partition any group G into disjoint conjugacy classes.

Example. In D₄, cl(H) = {R₀HR₀^-1 (= H), R₉₀HR₉₀^-1 (= V), R₁₈₀HR₁₈₀^-1 (= H), R₂₇₀HR₂₇₀^-1 (= V), HHH^-1, VHV^-1, DHD^-1, D’HD’^-1} = {H, V}. Similarly, cl(R_o) = {R₀}, cl(R₉₀) = cl(R₂₇₀) = {R₉₀, R₂₇₀}, etc.

Theorem. Let G be a finite group and let g be any element of G. Then, the number of conjugates of g is the index of the centralizer, that is, |cl(g)| = |G:Z(g)|

Proof.

Recall that H = Z(g), also denoted as C(g), is the set of all the elements that actually commute with this given element “g”, that is, {x ∈ G | xg = gx}.

Let R = G/C(g) {right cosets of C(g) in G}, and define Φ:G/C(g) → cl(g), Φ(C(g)x) = x^-1gx.

• Φ is well-defined. If C(g)x = C(g)y ⇒ xy^-1 ∈ C(g) ⇒ (xy^-1)g = g(xy^-1) ⇒ [*x^-1] y^-1g = x^-1gxy^-1 [*y] = y^-1gy = x^-1gxy^-1y ⇒ y^-1gy = x^-1gx.
• Φ is one-to-one. Suppose Φ(C(g)x) = Φ(C(g)y) ⇒ We need to show that C(g)x = C(g)y, that is, xy^-1∈ C(g) or, alternatively, (xy^-1)g = g(xy^-1)

Φ(C(g)x) = Φ(C(g)y) ⇒ x^-1gx = y^-1gy ⇒ [*y^-1] x^-1gxy^-1 = y^-1gyy^-1 ⇒ x^-1gxy^-1 = y^-1g ⇒ [*x] xx^-1gxy^-1 = xy^-1g ⇒ gxy^-1 = xy^-1g

• Φ is onto. Since both sets are finite sets (G is a finite group), this implies that Φ is bijective.

Therefore, Φ is isomorphism ⇒ |R| = |G:Z(g)| = |cl(g)| ∎

Corollary. If G is a finite group, then |cl(a)| divides |G|.

Proof.

Recall that the centralizer of a in G is a subgroup of G ⇒ the set of left (or right) cosets G:C(a) divides the order of G by Lagrange’s Theorem, and therefore |cl(a)| =[previous theorem, Z(a) is also denoted as C(a)] |G:Z(a)| divides the order of G.

The Class Equation. Let G be a nontrivial finite group. Suppose that a₁, a₂, ···, a_k are the representatives of the conjugacy classes that have size > 1. Then, $|G| = |Z(G)|+\sum_{i=1}^k |G:C(a_k)|$

Proof.

We have already demonstrated that |cl(g)| = |G:C(g)|, and C(g) is a subgroup of G, then |G| = |G:C(a_i)|·|C(a_i)|, then |G|/|C(a_i)| = |cl(a_i)| = |G:C(a_i)|

Since the conjugacy classes partition a group G, let b₁, ··· b_r be representatives of the conjugacy classes that have size 1

G = cl(b₁) ∪ ··· cl(b_r) ∪ cl(a₁) ∪ ··· cl(a_k) ⇒ [A partition is a union of disjoint classes] |G| = |cl(b₁)| + ··· + |cl(b_r)| + |cl(a₁)| + ··· + |cl(a_k)| = [Previous result: a∈ C(G)=Z(G) iff cl(a)={a}, in other words, the center of G is the set of all representatives of the conjugacy classes that have size 1] 1 + ··· 1 + |cl(a₁)| + ··· + |cl(a_k)| = |Z(G)| + |G:C(a₁)| + ··· + |G:C(a_k)| ⇒ $|G| = |Z(G)|+\sum_{i=1}^k |G:C(a_k)|$

Lemma. If G/Z(G) is cyclic, then G is Abelian.

Proof. (Based on Mathonline)

Recall that Z(G) ◁ G ⇒ the quotient G/Z(G) is well-defined ⇒[By assumption, G/Z(G) is cyclic] ∃g ∈ G: G/Z(G) = ⟨gZ(G)⟩

Let h ∈ G ⇒ hZ(G) ∈ G/Z(G) = ⟨gZ(G)⟩ ⇒ ∃n ∈ ℤ: hZ(G) = (gZ(G))ⁿ = gⁿZ(G), that is, hZ(G) = gⁿZ(G) ↭ (gⁿ)^-1h ∈ Z(G) ⇒ ∃i∈ Z(G): i = (gⁿ)^-1h ⇒ h = gⁿi. In other words, ∀h∈ G, ∃n ∈ ℤ & i∈ Z(G): h = gⁿi

∀h₁, h₂ ∈ G, we claim h₁h₂ = h₂h₁.

We already know ∃n₁, n₂ ∈ ℤ & i₁, i₂ ∈ Z(G): h₁ = g^n₁i₁ and h₂ = g^n₂i₂

h₁h₂ = g^n₁i₁g^n₂i₂ =[i₁ ∈ Z(G)] g^n₁g^n₂i₁i₂ = g^n₁+n₂i₁i₂ = g^n₂g^n₁i₁i₂ =[i₂ ∈ Z(G)] g^n₂g^n₁i₂i₁ =[i₂ ∈ Z(G)] g^n₂i₂g^n₁i₁ = h₂h₁ ∎

Theorem. Every p-group has a nontrivial center.

Proof.

Recall that given a prime number p, a p-group is a group in which the order of every element is a power of p. |G| = pⁿ, p prime and some n > 0.

By the class equation, $|G| = |Z(G)|+\sum_{i=1}^k |G:C(a_k)|$, but recall that |G:C(a_i)|=|G|/|C(a_i)| where C(a_i) is a subgroup, its order must divide |G|, |G|/|C(a_i)| = $\frac{p^n}{p^k}$, k < n.

$|G| - \sum_{i=1}^k |G:C(a_k)| = |Z(G)|$ Therefore, each term on the left is divisible by p, it follows that p also divides |Z(G)| ⇒ |Z(G)| ≠ 1 ∎

Theorem. If G is a group of order p², |G|=p², where p is prime, then G is Abelian.

Proof. By Lagrange and previous theorem, we know that (i) Z(G) is a subgroup of G, (ii) |Z(G)| divides |G|, so |Z(G)| =1, p or p², and (iii) Every p-group has nontrivial center, |Z(G)| = p or p²

1. |Z(G)| = p² ⇒ G = Z(G), i.e., G is Abelian.
2. |Z(G)| = p ⇒ [|G/Z(G)| = |G|/|Z(G)| = p²/p = p ] |G/Z(G)| = p ⇒ [Let p be a prime number, |G|=p ⇒ G is cyclic] G/Z(G) is cyclic ⇒ [Let G be a group and Z(G) be the center of G. If G/Z(G) is cyclic, then G is Abelian] G is Abelian.

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn (Abstract Algebra), and MathMajor.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. Andrew Misseldine: College Algebra and Abstract Algebra.