8 Estadística.
Contenido
8.1 ¡Si tu cabeza está a 0º y tus pies a 72º has triunfado!
8.2 Dibujando gráficas estadísticas.
8.3 Introducción a la Probabilidad.
8.4 Tablas de contingencia y Chi-cuadrado.
8.5 Análisis de varianza.
8.5.1 ANOVA de un factor
8.5.2 Análisis de varianza factorial.
8.5.3 ANOVA de un factor con medidas repetidas.
8.5.4 ANOVA de dos factores con medidas repetidas.
8.6. Contrastes estadísticos.
8.7 Análisis correlacional
8.8 Análisis de regresión lineal simple y múltiple.
8.1 ¡Si tu cabeza está a 0º y tus pies a 72º has triunfado!
¿Qué es la estadística? Existen dos definiciones básicas:
· Emulando a Benjamin Disraeli: “Hay varios tipos de mentiras: las mentirijillas de los más peques de la casa , las pequeñas mentiras, las medias verdades, las grandes mentiras y la estadística”.
, las pequeñas mentiras, las medias verdades, las grandes mentiras y la estadística”.
· Es la ciencia que dice que si mi vecino tiene dos coches y yo ninguno, los dos tenemos uno (George Bernard Shaw) o si mis pies están a 72º y mi cabeza a 0º estoy perfectamente en unos confortables 36º.
Bueno… a partir de estas “definiciones” podemos considerar dos tipos:
· Estadística descriptiva: trata sobre la recopilación de datos, su presentación, descripción y, aún más importante, el análisis e interpretación de dichos datos.
· Estadística inferencial: tiene como objeto de estudio inferir, deducir propiedades, estimar cómo se comporta una población a partir del análisis de los resultados extraídos a una pequeña muestra de la misma.
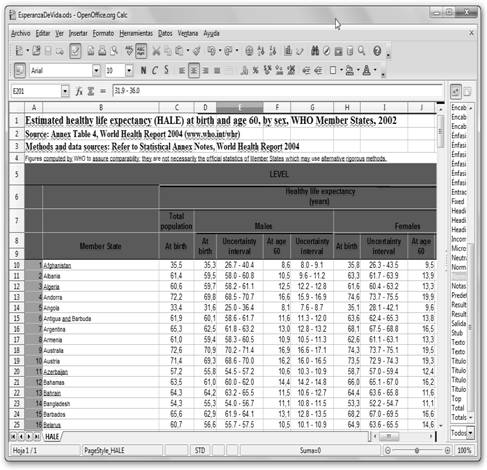
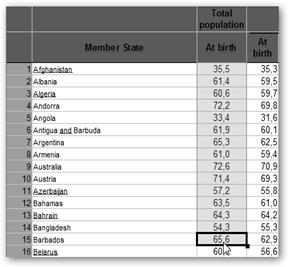
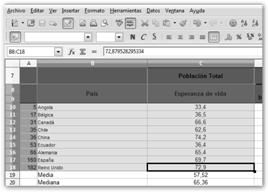
Tomemos como base las tablas que nos proporciona la Organización Mundial de la Salud, más concretamente, navega a su Web www.who.int/en/, selecciona Data and Statistics (datos y estadísticas), Life Expenctancy (esperanza de vida) y descarga alguno de los documentos adjuntos que se incluyen con datos “reales”.
Vamos a abrirlo con OpenOffice Calc. Recuerda como arrancar la aplicación: Inicio, Todos los programas, OpenOffice.org 3.2, OpenOffice Calc y donde encontrarlo es.openoffice.org. Las columnas que nos interesan son las siguientes: Member State (estado miembro de la Organización Mundial de la Salud), la segunda columna representa la esperanza de vida del país contando a todos los individuos, independiente de su género, mientras que la siguiente sería la de los varones de dicho país (Males, varones). La última que nos interesa es la que reza: At birth y Females, corresponde a la esperanza de vida de las mujeres en dicho país. Sin embargo, habrás observado que toda esta información es abrumadora  por su extensión. Tendremos que describirla, expresarla de una manera que nos sea más sencillo de interpretar.
por su extensión. Tendremos que describirla, expresarla de una manera que nos sea más sencillo de interpretar.
|
|
Para resumir los datos utilizamos la media. Se trata del promedio o más “formalmente” la suma ponderada de los valores de una variable por sus frecuencias:
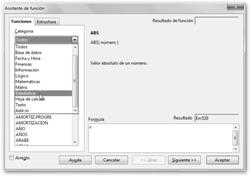
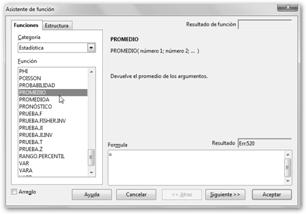
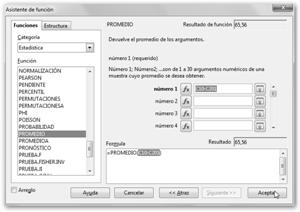
Donde ni es el número de veces que se presenta el valor xi, lo llamamos la frecuencia absoluta. Además, n es el tamaño de la población. Vale, Vale,… ¿Pero cómo lo obtenemos? Calculemos la esperanza de vida media de todos los países pertenecientes a la organización mundial de la salud. |
|
|
|
|
|
|
|
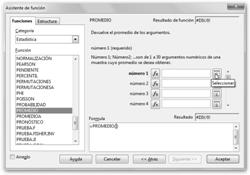
Observa que el asistente de función se ha minimizado para permitirte seleccionar los datos de tu hoja de cálculo. Recuerda que esta no es más que una matriz de celdas organizadas por filas (identificadas por números: 1, 2, 3, …) y columnas (en este caso se nombran por letras mayúsculas: A, B, C, …).
|
|
|
|
|
|
|
Hacemos lo mismo con otras medidas que nos ayuden a comprender mejor los datos, en particular: · Mediana: valor que se queda justo en medio · Moda: valor más frecuente observado en los datos. Observa que como son todos números decimales, ningún valor se repite, por lo que redondeamos con la función REDONDEAR. Por tanto, la función nos quedará como =MODA(REDONDEAR(c10:C201). |
|
El problema de si tú te comes dos pollos |
|
Veamos ahora como realizar todo esto con R. Se trata del software estadístico libre más potente que existe y es una alternativa real a SPSS. Incluye herramientas para el tratamiento y análisis de datos así como un entorno de programación. Al ser multiplataforma, puedes disponer de él en:
· Windows accediendo a su página web R http://cran.es.r-project.org/ y navegando por Windows, base, Download R 2.12.1 for Windows.
· Linux: navega por Linux y selecciona tu distribución favorita. En Ubuntu instala el paquete r-base. Se lanza con R desde el terminal y para salir, escribe q(). Al marcharte verás el mensaje: Save workspace image? [y/n/c] es la típica pregunta de cualquier aplicación sobre si quieres salvar tu trabajo, contesta “n”, no.
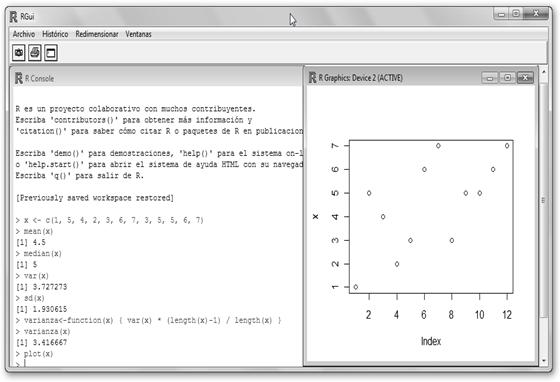
Creamos un vector “x” que va a representar las notas de ciertos alumnos. Ten en cuenta la sintaxis x <- c(valor1, valor2,….). Pedimos a R la media (mean(x)) y la mediana (median(x)). Desgraciadamente, R no contiene una función interna para calcular la moda. Cuidado ahora, curvas . ¡Con var(x) no conseguimos la varianza, sino la cuasivarianza y con sd(x), la cuasidesviación típica!
. ¡Con var(x) no conseguimos la varianza, sino la cuasivarianza y con sd(x), la cuasidesviación típica!
Sin embargo, no te líes , como varianza = cuasivarianza *
, como varianza = cuasivarianza *![]() y además como la función length calcula el número de elementos de un vector, definimos la función: varianza<-function(x) { var(x) * (length(x)-1) / length(x) }. Observa que hemos invocado la función recién creada con varianza(x) y también que nos grafique el vector de puntos: plot(x).
y además como la función length calcula el número de elementos de un vector, definimos la función: varianza<-function(x) { var(x) * (length(x)-1) / length(x) }. Observa que hemos invocado la función recién creada con varianza(x) y también que nos grafique el vector de puntos: plot(x).

Ahora hemos creado otro vector “y”. Mirando a la gráfica (plot(y)) puede confundirnos que no existan apenas diferencias, pero fíjate en el eje “y”. En este caso, oscila no entre 1 y 7 sino entre 4 y 7, es decir, los datos están menos dispersos. Podemos observar que al solicitar la varianza (varianza(y)≈1.08) obtenemos un valor significativamente menor que en el primer ejemplo 3.42. En otras palabras,  la media representa mucho mejor los datos en el segundo ejemplo que en el primero, pues los datos están más cercanos a él, menos dispersos. Otra forma de verlo es que entre la media y dos desviaciones típicas ([
la media representa mucho mejor los datos en el segundo ejemplo que en el primero, pues los datos están más cercanos a él, menos dispersos. Otra forma de verlo es que entre la media y dos desviaciones típicas ([![]() -2*D.T.,
-2*D.T., ![]() +2*D.T.]) están el 75% de los valores y entre la media y tres desviaciones típicas se encuentran el 89% de los datos.
+2*D.T.]) están el 75% de los valores y entre la media y tres desviaciones típicas se encuentran el 89% de los datos.
Ese es el problema de que tú te tomes dos huevos , yo cero “patatero” y la media nos dará uno, pero… ¿Qué dice la varianza? Que vale 1. ¿Y en el caso de que tanto tú como yo nos tomemos un solo huevo? Pues que la varianza vale 0, es decir, la media representa perfectamente a nuestros datos, nos describe exactamente los valores observados. ¡Ahí está la chicha, el meollo! La media es una medida central más, no nos dice toda la verdad.
, yo cero “patatero” y la media nos dará uno, pero… ¿Qué dice la varianza? Que vale 1. ¿Y en el caso de que tanto tú como yo nos tomemos un solo huevo? Pues que la varianza vale 0, es decir, la media representa perfectamente a nuestros datos, nos describe exactamente los valores observados. ¡Ahí está la chicha, el meollo! La media es una medida central más, no nos dice toda la verdad.

|
|
Imaginemos que al escribir el vector “y”, alguien se equivocó y tecleó 35 en vez de 7. ¿Qué ha sucedido? La media ha pasado de un representativo “5.5” a 7.92, es decir, un valor anómalo ha conseguido que nuestra media sea prácticamente inútil. |
|
Sin embargo, la mediana permanece inalterada. ¡Reivindiquemos la mediana amigos como una buena medida para representar nuestros datos! |
|
|
Mostremos varias funciones más: · min(y): mínimo del vector. · max(y): máximo del vector. · range(y): rango en el que oscila el vector, es decir, el mínimo y el máximo. · quantile(y): muestra los cuantiles del vector. · summary(y): presenta un resumen con el mínimo, el cuantil de orden ¼ Q1, la mediana (cuantil de orden ½), el cuantil de orden ¾ Q3 y el máximo. |
|
8.2 Dibujando gráficas estadísticas.
|
|
Veamos cómo realizar gráficos con Calc.
|
|
|
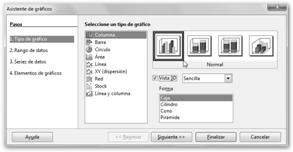
3. Elige en el menú Insertar la opción Gráfico… o pulsa alternativamente en el botón Gráfico.
4. Se lanzará un asistente donde seleccionarás el tipo de gráfico que deseas: columna, barra, circular, área, línea, etc., así como, otras opciones: Vista 3D y Forma. |
|
|
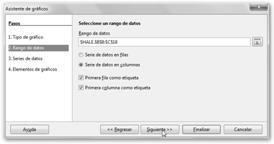
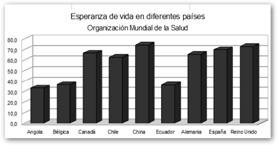
5. Seleccionamos el rango de datos, es decir, el conjunto de datos base para realizar la gráfica. En el ejemplo $HALE.$B$8:$C$18, es decir, se encuentran en la hoja $HALE y los datos comienzan en la celda B8 (País) y acaban en la celda C18 (72,9 el valor asociado al Reino Unido). |
|
En este ejemplo, las celdas B8 y B9 están combinadas, lo que hacía que Calc definiera como rango para valores-Y: $HALE.$B$9:$B$18 y de las categorías $HALE.$C$9:$C$18 lo que obviamente estaba mal y ha sido modificado en este paso. |
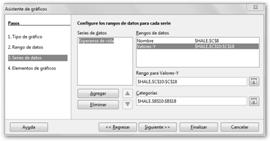
En el tercer paso del asistente se indica que el nombre se encuentra en $HALE.$C$8 (la columna C8, “Esperanza de vida”), las distintas categorías (Angola, Bélgica, España, etc.) en $HALE.$B$10:$B$18 (es decir, en el rango B10:B18) y el rango de valores se encuentra en $HALE.$C$10:$C$18 (el rango C10:C18: 33.4, 36.5, 66.6, etc.). ¡Cuídate de estos asistentes tan automáticos! A veces, tienen más peligro que un |
|
|
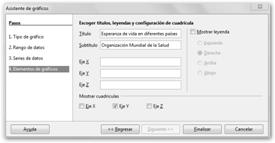
En el último paso, podemos escribir el título, subtítulo, si queremos mostrar la leyenda, dónde la situaríamos, etc. Cuando pulses en Finalizar, Calc te mostrará la gráfica realizada conforme a tus especificaciones. |
|
A partir de ahora, podemos modificar “a clic de ratón” el tipo de gráfico, el rango de datos, la posición y el tamaño, etc.
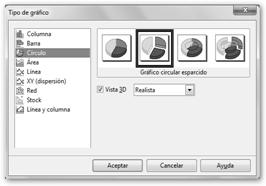
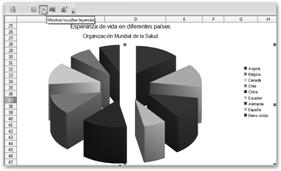
Elegiremos el tipo Gráfico circular esparcido con Vista 3D y Realista. |
Vamos a modificar el gráfico para ello haz doble clic sobre él. Luego con el botón derecho en el menú contextual selecciona Tipo de gráfico… |
|
Observa también que indicamos que queremos que se vea la leyenda pulsando Mostar/ocultar leyenda. |
|
|
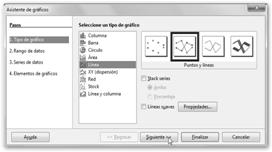
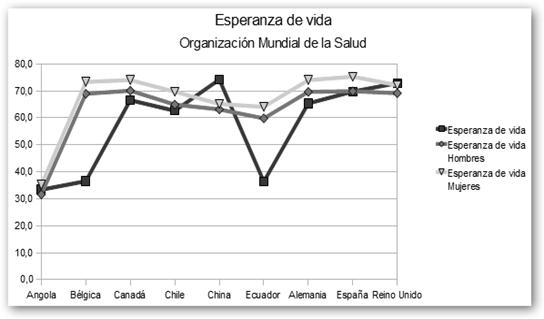
Vamos a realizar un gráfico más complicado. Veremos de los países ya seleccionados, no solo la esperanza de vida total sino también la esperanza de vida de los varones y las hembras y así podremos realizar comparaciones en función del género. |
Una vez seleccionado todo el rango (en el ejemplo B4:E13, País:72.1), navegamos por Insertar, Gráfico… y seleccionamos dentro del tipo Línea, Puntos y líneas. |
|
|
|
Observa el resultado obtenido: ¡Las mujeres viven más! Yo no sé quien fue el iluminado que dijo que son el sexo débil.
que dijo que son el sexo débil.
Dibujemos ahora gráficos estadísticos con R. Utilizaremos los datos del Barómetro de Opinión Pública de Andalucía, 2009. Más concretamente, el ítem relativo a cuáles son los tres problemas más importantes que los sujetos consideran que Andalucía tiene en este momento.
|
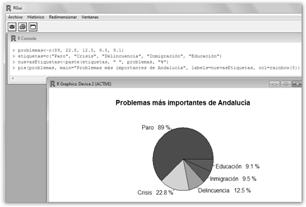
En un vector problemas guardaremos los porcentajes, son: 89,0% (paro), 22,8% (crisis económica), 12,5% (delincuencia), 9,5% (inmigración) y 9,1% (educación): problemas<-c(89, 22.8, 12.5, 9.5, 9.1) En otro vector etiquetas, los nombres asociados a dichos porcentajes: etiquetas=c("Paro", "Crisis", "Delincuencia", "Inmigración", "Educación") |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Con barplot(problemas, main="Problemas más importantes de Andalucía", ylab="Porcentaje de personas", names.arg=etiquetas, col=rainbow(5)) dibujamos el gráfico de barras. Observa los argumentos: vector con los datos (problemas), título del gráfico (main=”Problemas más importantes de Andalucía”), etiquetas del eje “y” (ylab) y de las barras (names.arg=etiquetas) y utilizaremos para los colores de las barras el arcoíris (col=rainbow(5)). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Creemos ahora un diagrama de tartas con R. En primer lugar, hemos creado un nuevo vector nuevasEtiquetas<-paste(etiquetas, " ", problemas, "%"), con el fin de que en las etiquetas aparezca no sólo el nombre, sino su valor numérico y el signo de porcentaje (p.e. Paro 89%). |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Considera que lo que hemos realizado es la concatenación con paste de los vectores etiquetas y problemas, un espacio en blanco “ “ y el porcentaje “%”. Dibujamos una tarta con pie(problemas, main="Problemas más importantes de Andalucía", labels=nuevasEtiquetas, col=rainbow(5)). Los argumentos de pie son: vector con los datos (problemas), título de la gráfica (main="Problemas más importantes de Andalucía"), etiquetas (labels=nuevasEtiquetas) y colores de la tarta (col=rainbow(5)). Para modificar los colores prueba las siguientes combinaciones: tipo temperatura col=heat.colors(5) o crea un vector de colores: colores<-c("blue", "yellow", "red", "orange", "brown") y sustituye la llamada anterior por pie(problemas, main="Problemas más importantes de Andalucía", labels=nuevasEtiquetas, col=colores). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
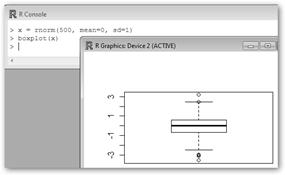
Con R podemos generar un vector con 500 números con la distribución normal de media 0 y desviación típica 1 con la orden x=rnorm(500, mean=0, sd=1). A continuación, dibujamos un diagrama de cajas con boxplot(x). La caja está comprendida entre el primer y el tercer cuartil, la línea central es la mediana. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
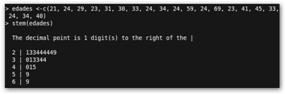
R también nos permite realizar árboles de tallo y hoja con stem. En este ejemplo, los tallos son las decenas (The decimal point is 1 digit(s)…) y las hojas las unidades. La mayoría de los sujetos tienen edades comprendidas entre 20 y 40 años. Sólo dos son más mayores: tienen 59 y 69 años respectivamente. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Veamos un ejemplo más avanzado. Mostraremos el número de parados registrados en el INEM desde 1996 hasta el 2010. Los datos estarán almacenados en el archivo parados.txt y tendrán el siguiente formato: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
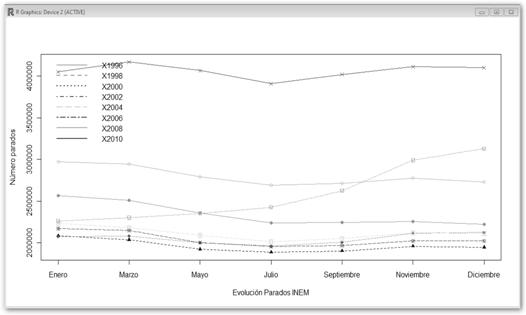
Se organiza en filas (años donde se toman los datos) y columnas donde se registra el número de parados en un año en los meses de Enero, Marzo, Mayo, Julio, Septiembre, Noviembre y Diciembre. Más interesante aún, vamos a escribir un script en R para evitarnos teclear todas las órdenes por consola y si nos equivocamos, no tendremos que reescribirlas de nuevo sino solo necesitaremos modificar el script y volver a lanzarlo. Crea una archivo con extensión .R como, por ejemplo, miScript.R y escribe en él lo siguiente: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
- parados <-read.table("C:/parados.txt ", header=T)
- plot(parados$X1996, type="o", xaxt="n", ylim=range(parados), col="violet", xlab="Evolución Parados INEM", ylab="Número parados")
- axis(1, at=1:7, lab=c("Enero", "Marzo", "Mayo", "Julio", "Septiembre", "Noviembre", "Diciembre"))
- colores<-c("violet","green","blue","purple","pink","brown","orange","red")
- lines(parados$X1998, type="o", pch=16, lty=1, col="green")
- lines(parados$X2000, type="o", pch=17, lty=2, col="blue")
- lines(parados$X2002, type="o", pch=18, lty=3, col="purple")
- lines(parados$X2004, type="o", pch=11, lty=4, col="pink")
- lines(parados$X2006, type="o", pch=13, lty=5, col="brown")
- lines(parados$X2008, type="o", pch=14, lty=6, col="orange")
- lines(parados$X2010, type="o", pch=4, lty=7, col="red")
- legend("topleft", names(parados),col=colores, lty=1:7, lwd=2, bty="n")
|
Expliquemos línea a línea el script realizado:
|
|
|
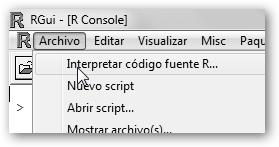
Para ejecutar el script que hemos realizado basta con navegar por Archivo, Interpretar código fuente R…, tal como se ilustra en la figura, e indicar dónde está nuestro script. Observa el resultado obtenido. |
|
Sin embargo, conocer si esa representación de los datos es conforme a la dura realidad en la que se ve sumida España se escapa al ámbito de la ciencia exacta de la Estadística. Por ejemplo, ¿representa las personas que se han registrado en el INEM el número real de parados?, ¿es mejor medida la Encuesta de Población Activa?, etc.
|
|
Las siguientes órdenes te resultarán de utilidad. Si quieres entrar en R escribe R en la consola y para salir q(). Para buscar ayuda sobre una determinada “orden” escribe help(orden) o ?orden y con help.start() mostrará la ayuda completa. |
8.3 Introducción a la Probabilidad.
|
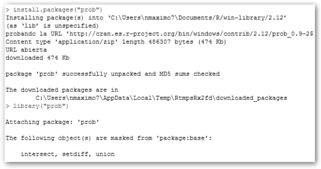
Para introducirte en la Probabilidad utilizaremos también R. Necesitamos instalar install.packages("prob") y cargar el paquete prob library(“prob”) tal como se ve en la figura (para mayor información consulta 8.5). |
|
|
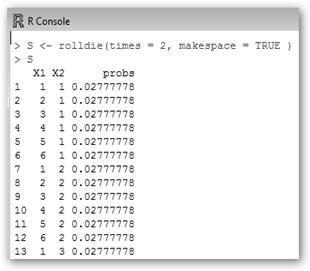
Veamos las diferentes posibilidades que podemos obtener tirando dos veces una moneda y una única vez un dado así como sus probabilidades asociadas. Al lanzar dos monedas tenemos cuatro posibilidades: H (heads, caras) H; T (tails, cruces) H; H T y T T, todas tienen la misma probabilidad 1/4. En un dado existen seis resultados posibles (1,2,…6) todos con probabilidad 1/6. Recuerda que para calcular la probabilidad se divide el número de casos posibles (1 en ambos casos) por el número de posibilidades (4 y 6 respectivamente). |
La figura continúa hasta las 36 posibles combinaciones.
|
|
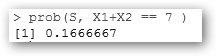
Tiremos la moneda dos veces: ¿Cuál es la probabilidad de que sumemos 7 con los dos dados? Pues las posibilidades son: 1, 6 (y 6, 1, luego contamos por 2); 2, 5 (5, 2); 3, 4 (4, 3), es decir, 6/36=0.166… ¿Y de que nos salgan dos veces 6? Pues teclea prob(S, X1==6 & X2==6 ) y obtendrás 0.02777778. Lo que es lógico pues se trata de sucesos independientes y P(A∩B)=P(A)*P(B)=1/6*1/6=1/36. |
|
|
¿Y de que nos salga en el primero un 1 o un 6? Escribe en R: prob(S, X1==1 | X1==6 ) y obtendrás 0.333333, hay dos posibilidades entre 6, 1/3. |
|
|
¿Cuál es la probabilidad de que nos salga el mismo valor de la moneda en los dos dados, dado que hemos obtenido 8? |
|
|
Estamos trabajando con probabilidad condicionada, es decir, a la probabilidad de un suceso (A, los dos dados tengan el mismo valor) dado que haya ocurrido otro (la suma de los dos dados es 8). Luego, utilizaremos las fórmulas: P(A/B)= Observa que P(B)=5/36, pues hay sólo 5 posibilidades: 2, 6; 6, 2; 3, 5; 5, 3 y 4, 4. La probabilidad de Otros ejemplos: probabilidad de que el primer dado sea 6 dado que éste haya salido par prob(S, X1==6, given = (X1%%2==0)), es 1/3; de que sea 6 el primero dado que el segundo ha salido par y la suma de ambos es mayor que 8 prob(S, X1==6, given = ((X2%%2==0) & (X1+X2>8)) ), también es 1/3; de que sea 6 el primero dado que la suma de ambos haya salido mayor que 8 y el segundo es impar prob(S, X1==6, given = ((X2%%2!=0) & (X1+X2>8)) ), resulta en ½, etc. |
|
|
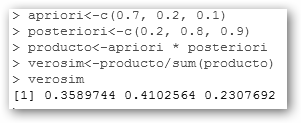
¡Liemos más la cosa! Un profesor tiene tres tipos de estudiantes: torpes (0.7), listos (0.2) y superdotados (0.1). Típicamente las probabilidad de que estos grupos aprueben un examen son: 0.2, 0.8 y 0.9 respectivamente. Tiene un examen aprobado pero nadie lo ha firmado, ¿a qué grupo pertenece? |
Las probabilidades de pertenecer el examen a los distintos grupos están representadas en el vector versosim. En particular, el primer elemento 0.3589 representa la probabilidad de que sea uno del grupo de los torpes. |
|
Pues utilizaremos el Teorema de Bayes para resolverlo. ¿Recuerdas la fórmula? P(B/Ai)= Las probabilidades a priori de pertenecer a un grupo son apriori<-c(0.7, 0.2, 0.1). Las probabilidades a posteriori P(B/Ai) las hemos llamado posteriori<-c(0.2, 0.8, 0.9). Luego, hemos multiplicado ambas y sumado el vector resultante para obtener la probabilidad del denominador del teorema de Bayes que no es más que P(B), es decir, la probabilidad de aprobar (sum(producto)) y es igual a 0.39. |
|
8.4 Tablas de contingencia y Chi-cuadrado.
Cuando nos preguntamos sobre la relación de dos variables categóricas, léase sexo, raza, si el individuo es zurdo o diestro, fumador, etc., utilizamos tablas de contingencia para organizar y analizar los datos. Veamos un ejemplo en el que se tienen dos variables: género y fumar.
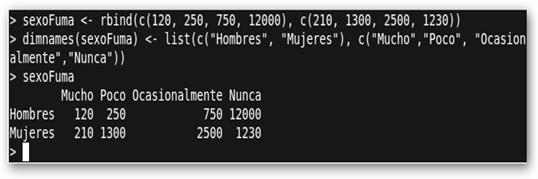
|
Veamos los pasos a seguir: 1. sexoFuma <- rbind(c(120, 250, 750, 12000), c(210, 1300, 2500, 1230)): Creamos una matriz sexoFuma con los datos. 2. dimnames(sexoFuma) <- list(c("Hombres", "Mujeres"), c("Mucho","Poco", "Ocasionalmente","Nunca")): asignamos etiquetas a dicha matriz para mejorar su lectura y comprensión 3. sexoFuma: finalmente la mostramos |
|
|
4. chisq.test(sexoFuma): contrastamos la hipótesis de que las variables están relacionadas. Nos devuelve un estadístico chi-cuadrado de Pearson 8658.464. En la distribución χ2 con tres grados de libertad tiene una probabilidad asociada de p<2.2e-16<.05. Debemos rechazar la hipótesis de independencia. |
En “cristiano” sería que las variables están relacionadas. El problema ahora es ¿cómo? Puedes observar los datos o utilizar la gráfica que te muestra mosaicplot(sexoFuma, shade=T) para hacerte una idea. |
8.5 Análisis de varianza.
8.5.1 ANOVA de un factor
|
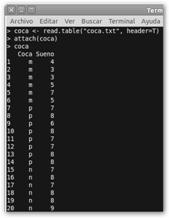
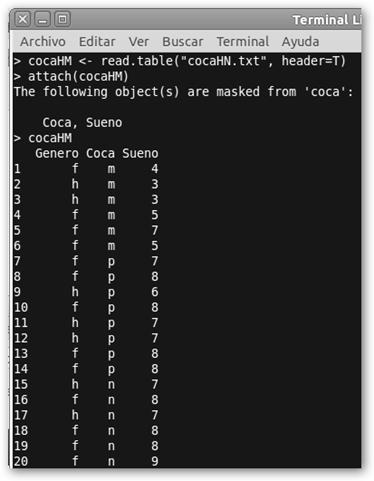
coca.txt Coca Sueno m 4 m 3 m 3 m 5 m 7 m 5 p 7 p 8 p 6 p 8 p 7 p 7 p 8 p 8 n 7 n 8 n 7 n 8 n 8 n 9 |
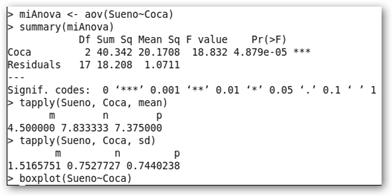
Sea la siguiente tabla (coca.txt) que representan el número de horas “Sueno” que informan que duermen un número de sujetos que consumen una cantidad de refresco de cola “Coca”. Más concretamente el consumo de coca se ha cuantificado como: m (mucho, más de 1 litro), p (poco, entre una lata y un litro), n (nada, no consumen refrescos de cola). Se quiere conocer el impacto del consumo del refresco en el sueño y, en su caso, cual es la medida del consumo ideal. Esto se realiza con un ANOVA con una variable independiente o factor V. I. (que es categórica: m, p y n) “Coca” y una variable dependiente V. D. “Sueño” (cuantitativa) en la que se comparará la variable independiente. El ANOVA realiza contrastes de hipótesis para conocer si las diferencias de medias en cada uno de los grupos de la V. I. son iguales. Si fueran iguales, los grupos estudiados no difieren en la V. D. y nuestras dos variables serían ciertamente independientes. ¡Basta de charla que parece que nos han dado cuerda, con más rollo que Calleja paseando al perro de Scottex! |
||
|
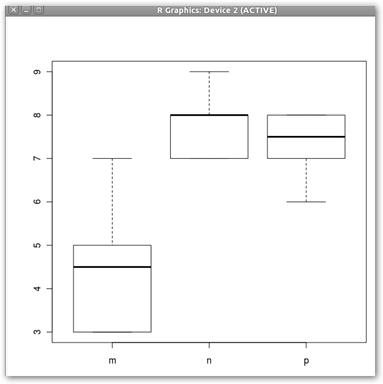
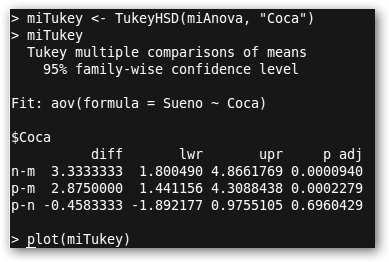
4. La madre del cordero, el ANOVA: miAnova <- aov(Sueno~Coca). Fíjate: aov(V.D~V.I.). 5. summary(miAnova) muestra toda la información del ANOVA. 6. tapply(Sueno, Coca, mean) y tapply(Sueno, Coca, sd) nos permiten conocer las medias y las desviaciones típicas respectivamente en los distintos grupos de la V.I. 7. Se muestra en la figura el gráfico solicitado con boxplot(Sueno~Coca) para poder comprender mejor que está pasando en los diferentes grupos. Destaca sobremanera el grupo que consume mucha “m” cola. 8. Vamos a realizar el estudio de Tukey para encontrar las diferencias entre los grupos en el consumo de coca: miTukey<- TukeyHSD(miAnova, “Coca”). |
Sigue los siguientes pasos:
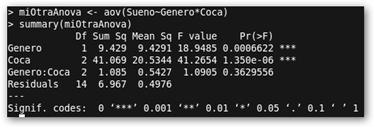
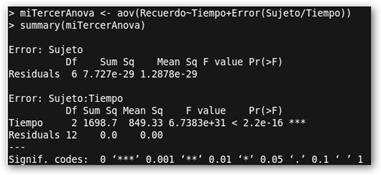
Nota: El carácter ~ puedes encontrarlo pulsando simultáneamente las teclas AltGr y 4 y luego la barra espaciadora. Lo más importante es que se ha obtenido que los efectos de la Coca son estadísticamente significativos. El nivel crítico asociado al estadístico F (18.832) es menor que .05 (Pr(>F)=4.879e-05). Se rechaza la hipótesis de igualdad de medias y, en consecuencia, los grupos comparados difieren en su sueño en función del consumo de refresco de cola. |
|
|
|
La conclusión sería: beber un poco de refresco de cola no hace daño pero sin excederse: ¡como casi cualquier cosa en la vida, casi todo es bueno en su justa medida! |
|||
|
Por cada posible combinación obtenemos una columna: diff (diferencias de medias), lwr y upr (límites inferiores y superiores del intervalo de confianza) y padj (el valor de p). Son significativas las diferencias entre los grupos que no consumen nada y mucho y los que consumen poco y mucho, pero no entre los que consumen poco o nada. |
|
||
|
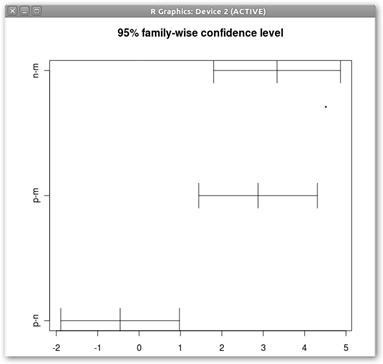
9. Al dibujar con plot(miTukey) este análisis, sólo el grupo p-n incluye en su intervalo de confianza el cero, lo que no nos permite rechazar la hipótesis nula de igualdad de medias. |
|
|
|
|
|
|||
8.5.2 Análisis de varianza factorial.
|
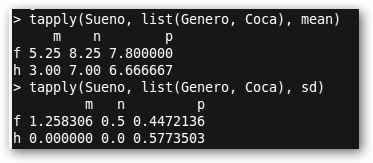
Genero Coca Sueno f m 4 h m 3 h m 3 f m 5 f m 7 f m 5 f p 7 f p 8 h p 6 f p 8 h p 7 h p 7 f p 8 f p 8 h n 7 f n 8 h n 7 f n 8 f n 8 f n 9 La línea de código que diferencia este estudio del previo es: miOtraAnova <- (Sueno~Genero*Coca). En la siguiente línea summary(miOtraAnova) obtenemos un resumen de la información encontrada por R. Todas las columnas tienen los mismos significados que en el apartado anterior y en el ejemplo que nos ocupa son significativos los efectos individuales de Genero y Coca pero no de la interacción entre ambos. tapply(Sueno, list(Genero, Coca), mean) y tapply(Sueno, list(Genero, Coca), sd) nos permiten conocer las medias y las desviaciones típicas en los distintos grupos; por ejemplo, las mujeres (f) que toman mucha (m) cola duermen en media 5.25. |
Queremos determinar si el sexo es ahora un factor determinante y el efecto de la combinación entre el consumo de coca y el género. Tenemos pues un ANOVA de dos factores: Genero (f, female, mujer; h hombre) y Coca y una V.D. Sueño. En este análisis factorial estudiaremos: los efectos del género, del consumo de refrescos de cola y de la interacción del género y el consumo de coca en el sueño. Volvemos a extraer los datos de un fichero (véase la columna de la izquierda) llamado cocaHN.txt. “f m 4” se lee como que una mujer que tomó mucho refresco de cola informa de dormir unas cuatro horas.
|
|
|
|
|
|
8.5.3 ANOVA de un factor con medidas repetidas.
|
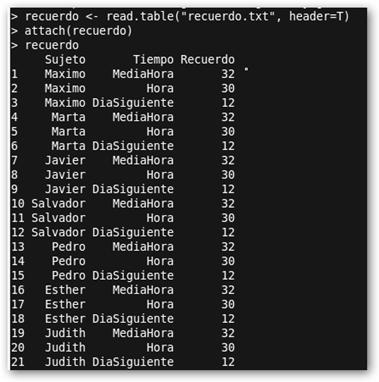
Fichero: Recuerdo.txt Sujeto Tiempo Recuerdo Maximo MediaHora 32 Maximo Hora 30 Maximo DiaSiguiente 12 Marta MediaHora 32 Marta Hora 30 Marta DiaSiguiente 12 Javier MediaHora 32 Javier Hora 30 Javier DiaSiguiente 12 Salvador MediaHora 32 Salvador Hora 30 Salvador DiaSiguiente 12 Pedro MediaHora 32 Pedro Hora 30 Pedro DiaSiguiente 12 Esther MediaHora 32 Esther Hora 30 Esther DiaSiguiente 12 Judith MediaHora 32 Judith Hora 30 Judith DiaSiguiente 12 La chicha vuelve a estar en la línea: miTercerAnova <- (Recuerdo~Tiempo+ Error(Sujeto/Tiempo)). Como el factor “Tiempo” está vinculado con el “Sujeto” debemos especificar el término de error en el análisis: Error(Sujeto/Tiempo) |
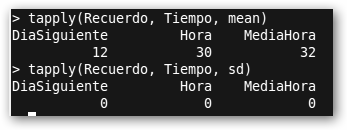
Te presento otro experimento. A los sujetos se les presentan una lista con un número de palabras que tienen que memorizar. Al cabo de media hora, una hora y al día siguiente se les cuestiona sobre la calidad de su recuerdo que se mide como el número de palabras que recuerdan. En este caso existe un factor o V.I. “Tiempo” con tres niveles (MediaHora, Hora, DiaSiguiente) y la V.D. “Recuerdo”. Además todos los sujetos repiten en el factor, es decir, se les toma medidas en los tres niveles del factor. Maximo MediaHora 32 se lee como “Máximo recordaba a la media hora 32 palabras”. El principio del estudio es un calco idéntico: “Igualico, Igualico que el difunto de su agüelito”.
|
|
El análisis muestra que el factor tiempo incide estadísticamente de forma significativa en la calidad del recuerdo de los sujetos. Observa que el valor de F (6.73831e+31) tiene una significación (Pr(>F)=2.2e-16) menor que .05. |
|
|
¡No era de extrañar! Observa como las medias solicitadas con tapply chillan este resultado. En particular, al día siguiente las personas olvidan mucho más. |
Si ya sé, la desviación típica es un perfecto cero…Los datos están más amañados que una escopeta de feria, las máquinas tragaperras o los bolsillos de un mago. |
8.5.4 ANOVA de dos factores con medidas repetidas.
|
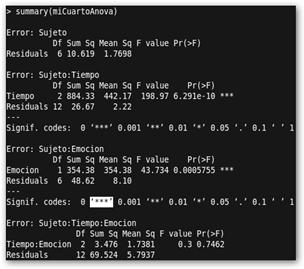
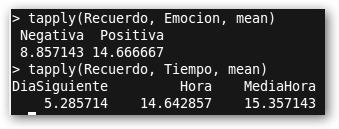
Sujeto Tiempo Emocion Recuerdo Maximo MediaHora Positiva 20 Maximo MediaHora Negativa 12 Maximo Hora Positiva 20 Maximo Hora Negativa 10 Maximo DiaSiguiente Positiva 10 Maximo DiaSiguiente Negativa 2 Marta MediaHora Positiva 17 Marta MediaHora Negativa 12 Marta Hora Positiva 16 Marta Hora Negativa 14 Marta DiaSiguiente Positiva 8 Marta DiaSiguiente Negativa 4 Javier MediaHora Positiva 18 Javier MediaHora Negativa 13 Javier Hora Positiva 20 Javier Hora Negativa 10 Javier DiaSiguiente Positiva 8 Javier DiaSiguiente Negativa 3 Salvador MediaHora Positiva 17 Salvador MediaHora Negativa 11 Salvador Hora Positiva 21 Salvador Hora Negativa 11 Salvador DiaSiguiente Positiva 7 Salvador DiaSiguiente Negativa 1 Pedro MediaHora Positiva 20 Pedro MediaHora Negativa 10 Pedro Hora Positiva 18 Pedro Hora Negativa 9 Pedro DiaSiguiente Positiva 6 Pedro DiaSiguiente Negativa 2 Esther MediaHora Positiva 18 Esther MediaHora Negativa 17 Esther Hora Positiva 15 Esther Hora Negativa 14 Esther DiaSiguiente Positiva 8 Esther DiaSiguiente Negativa 2 Judith MediaHora Positiva 15 Judith MediaHora Negativa 15 Judith Hora Positiva 14 Judith Hora Negativa 13 Judith DiaSiguiente Positiva 12 Judith DiaSiguiente Negativa 1 Observa que los efectos tanto del “Tiempo” como de la “Emoción” son significativos estadísticamente pero no de la interacción entre Tiempo y Emoción. Puede observarse claramente (volvemos a solicitar las medias con tapply de los diferentes grupos) que los sujetos recuerdan mejor las palabras positivas y que conforme pasa el tiempo, disminuye la calidad del recuerdo. |
¿Y si además de contar como factor el “Tiempo” tuviéramos un segundo? El factor “Emoción” mide los sentimientos que determinada palabras nos provocan: positivos (vacaciones, amor, música, etc.) o negativos (enfermedad, muerte, accidente, etc.). Se trata de un ANOVA de dos factores (Tiempo, Emoción) con medidas repetidas, es decir, los sujetos pasan por todas las combinaciones de los dos factores. Maximo MediaHora Positiva 20 se lee como: “el sujeto Máximo a la media hora recordaba 20 palabras positivas”.
El meollo es: miCuartoAnova <-aov(Recuerdo~(Tiempo*Emocion)+Error(Sujeto/(Tiempo*Emocion))) porque queremos medir no sólo los efectos individuales de Tiempo y Emoción sino también de su interacción. Además, tendremos que sumar a la ecuación, análogamente al caso anterior, el error Error(Sujeto/(Tiempo*Emocion)).
|
8.6. Contrastes estadísticos.
|
La distribución binomial es una distribución de probabilidad que cuenta el número de éxitos en una sucesión de “n” experimentos independientes donde la probabilidad de éxito es fija. Por ejemplo, tiramos un dado, la probabilidad de que nos salga un número es siempre 1/6. Realicemos el contraste de hipótesis sobre la probabilidad de éxito de un experimento de Bernoulli. |
|
|||
|
En el ejemplo, tecleamos: binom.test(c(10, 50), p=1/6). Es decir, contrastamos el éxito de un experimento en el que ejecutado 60 veces, 10 nos sale un determinado resultado (por ejemplo, si fuera un dado, nos sale un número), 50 nos saldría cualquier otro. Cada ensayo es independiente y tiene una probabilidad 1/6. El resultado es p-value=1, es decir, no rechazamos la hipótesis nula, la probabilidad de éxito de nuestro experimento es 1/6 (≈0.17). Sin embargo, si escribimos binom.test(c(30, 30), p=1/6), es decir, obtenemos el mismo resultado 30 veces sobre 60 y queremos contrastar que la probabilidad de éxito es 1/6, R nos devuelve un p-value 2.785e-09, prácticamente cero, se rechaza la hipótesis nula, 1/6 no es la probabilidad de éxito. También, devuelve un intervalo de confianza de la probabilidad de éxito [0.36, 0.63] y la probabilidad estimada de éxito ½, es decir, parece que se trata de un experimento de cara y cruz. Prueba ahora: binom.test(c(30, 30), p=1/2) ¿Qué sucede? Pues que no se rechaza la hipótesis nula. |
||||
|
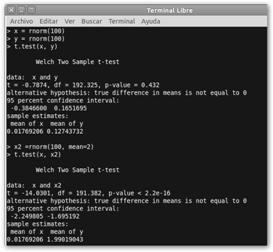
Simulamos en “x” e “y” datos de sendas distribuciones normales que por defecto tienen media 0. ¿Podremos suponer que las medias de las dos poblaciones a las que supuestamente pertenecen estas muestras son iguales? Realizamos el test de Welch y observamos que no rechazamos la hipótesis nula de igualdad de medias (H0: η1=η2). Sin embargo, si la comparamos con otra muestra x2 donde se obtienen los datos de una distribución normal de media 2, el test rechaza la hipótesis nula: x y x2 son muestras de poblaciones con medias diferentes. |
|
|||
|
Con var.test(x,y) no rechazamos la hipótesis nula de igualdad de varianza (H0: σ2x= σ2y) (p=0.9626). Luego, podemos solicitar t.test(x, y, var.equal=T), es decir, el test de Student pues tenemos igualdad de varianzas (H0: ηx= ηy). Se obtiene que no se rechaza tampoco la hipótesis nula de igualdad de medias. |
Si ejecutas t.test(x, mu=0), es decir, H0: ηx= 0, obtendrás que no se rechaza dicha hipótesis nula. Con t.test(x, mu=1) si se rechaza H0: ηx= 1. |
|||
|
Observa ahora que tras comprobar que “x” e “y” son dos muestras con igualdad de varianzas realizamos el siguiente test de Student: t.test(x, y, var.equal=T, alternative="less"). En esta ocasión queremos contrastar la hipótesis alternativa de que la media de “x” es menor que la de “y” (Ha: η1< η2) y se rechaza la hipótesis nula. Podemos suponer que la media de la primera población de donde se ha extraído la muestra es menor que la de la segunda. |
|
|||
|
Para seguir avanzando, vamos ahora a instalar el paquete PASWR. En él se encuentran numerosos datos del libro Probability and Statistics with R de Ugarte, Militino y Arhnholt. Se realiza con las siguientes órdenes: · install.packages("PASWR"): descarga e instala el paquete PASSWR de los repositorios; tendrás que indicar una ciudad cercana a tu ubicación. · library("PASWR"): carga el paquete, listo para ser utilizado. Con library() podrás consultar todas los paquetes disponibles. |
||||
|
En particular nos interesa de PASWR una tabla Fertilize con los datos de las alturas de plantas fertilizadas con dos métodos: cross (cruzada) y self (autofertilización). Veamos las tres instrucciones que hemos solicitado:
La idea es realizar inferencia estadística. ¿A que nos referimos? Idealmente estudiaríamos toda la población, es decir, todas las cosechas y comprobaríamos cual es el mejor sistema. Sin embargo, esto suele ser inviable económicamente y muy inconveniente. Lo que se realiza es extraer un subconjunto de datos de la población (muestra) e intentar extrapolar conclusiones respecto a la población general. En particular, estos datos son sólo una muestra de la población total. |
|
|||
|
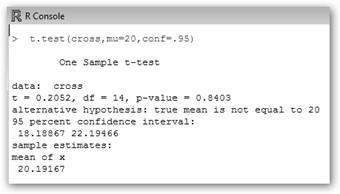
Vamos a realizar un test en el que preguntemos si podemos asumir que la media de la población es un cierto valor, por ejemplo, 20. Realiza los siguientes pasos: 1. attach(Fertilize): enlazamos la base de datos o tabla Fertilize a R para que podamos invocar sus variables cómodamente. 2. t.test(cross, mu=20, conf=.95): realizamos un contraste de hipótesis donde tenemos dos hipótesis:
La hipótesis nula Ho es que la media |
Observa que nos indica el valor de t, los grados de libertad, y el valor de probabilidad (p-value= 0.8403), es decir, no se rechaza la hipótesis nula de que la media de la población total sea 20. Además, obtenemos el intervalo de confianza en donde se encuentra la media [18.19, 22.19]. Sin embargo, prueba con t.test(cross, mu=17, conf=.95) y obtendrás una p<0.05, con lo que diríamos que estamos estadísticamente seguros que la media de la población no es 17. |
|||
|
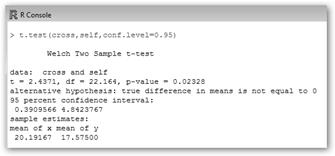
¿Serán los dos métodos de fertilización iguales? Una forma de saberlo es realizar un test que pregunte si las diferencias de medias son significativas. Esto se realizaría con la orden: t.test(cross, self, conf.level=0.95). ¡Observa que hay una probabilidad de 2.328% de equivocarse! |
En este ejemplo la hipótesis nula es que ambas medias son iguales, H0: η1=η2. Como p-value=0.02328<0.05 se rechaza dicha hipótesis, podemos asegurar que las medias de las poblaciones son diferentes y, por tanto, los métodos obtienen diferentes resultados. |
|||
|
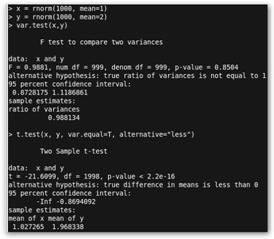
Observa que R no asume igualdad de varianzas por defecto. Si quieres asumirlo el test se realizaría con la orden t.test(cross,self,var.equal=T,conf.level=0.95), donde var.equal=T indica que suponemos igualdad de varianzas en las dos poblaciones. Para comprobar que puedes realizar esta suposición ejecuta la orden var.test(cross, self). |
La hipótesis nula en este test es la igualdad de varianzas de las dos poblaciones (H0: σ2x= σ2y) y la rechazamos (p-value=0.04208<0.05). Nos tenemos que conformar con la hipótesis alternativa: las varianzas de las poblaciones son diferentes y el test de Welch (opción por defecto en R con t.test). |
|||
|
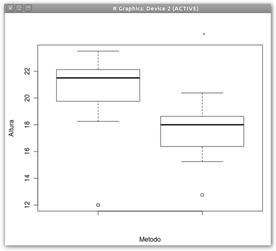
Con boxplot(cross, self, ylab="Altura", xlab="Metodo") nos hacemos una idea de las muestras. En este caso, parece claro que las medias de sus poblaciones no debían ser idénticas.
|
|
|||
|
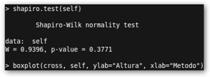
Como último apunte el test de Shapiro-Wilk comprueba la normalidad de los datos de la muestra que es requisito de los contrastes realizados. En la figura, se observa que p>.05 y no rechazamos la hipótesis nula de que los datos provienen de una distribución normal (que como su propia palabra lo dice es lo más “normal” o habitual de encontrarse). El mismo resultado (con p-value más próximo a 1) nos sale obviamente si escribimos: shapiro.test (rnorm(1000, mean = 1, sd = 2)) pero no con shapiro.test(rchisq(1000, 2)) donde los datos son extraídos de una χ2 con dos grados de libertad. |
||||
|
Hay una base de datos disponibles llamada Aggression que mide el comportamiento agresivo. Existen dos grupos:
|
Como podemos comprobar no podemos rechazar la hipótesis nula, es decir, no estamos seguros que la exposición a la violencia incite al comportamiento agresivo. |
|||
8.7 Análisis correlacional
|
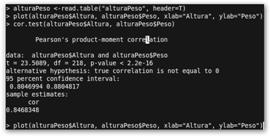
Un análisis correlacional mide el grado en el que dos variables cuantitativas están relacionadas o asociadas. Veamos un ejemplo. 1. Crearemos un archivo de datos que llamaremos alturaPeso.txt con dos columnas: Altura y Peso. El archivo de datos se muestra sólo parcialmente por su abultado tamaño. 2. Leemos dicho archivo de datos con la orden alturaPeso <-read.table("C:/alturaPeso.txt", header=T), es decir, indicamos la ruta donde se encuentra el archivo de datos y que tiene una cabecera. |
Altura Peso 1.61 72.21 1.61 65.71 1.70 75.08 1.65 68.55 1.72 70.77 1.63 77.18 1.76 81.21 1.67 75.71 […] |
|
|
A “vista de pájaro” parece existir una relación positiva entre la Altura y el Peso. Conforme aumenta la altura, también lo hace el peso. |
|
|
|
El análisis correlacional realizado con cor.test(alturaPeso$Altura, alturaPeso$Peso) encuentra una asociación positiva con un coeficiente de correlación r≈0.85>0. Esta relación es estadísticamente significativa pues p=2.2e-16<0.05. Además, R devuelve el estadístico t de Student (23.5089) de la prueba, los grados de libertad (218) y el intervalo de confianza [0.80, 0.88]. ¿Quieres obtener que dos variables no estén relacionadas? Teclea: x = rnorm(1000); y = rnorm(1000); cor.test(x,y) y obtendrás algo como: t = -0.5186, df = 998, p-value = 0.6042>0.05, cor =-0.01641383. También, puedes obtener los coeficientes Tau-b de Kendall y Spearman con: cor.test(x,y, method=c("kendall")) y cor.test(x,y, method=c("spearman")). |
||
8.8 Análisis de regresión lineal simple y múltiple
Hagamos ahora un análisis de regresión lineal muy sencillo prosiguiendo con el estudio anterior.
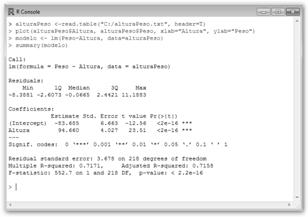
Se trata de conocer la relación existente entre una variable llamada dependiente (Y) y una o más variables independientes o predictoras (X1, X2, …Xn). Más formalmente, en un análisis de regresión lineal simple tendríamos una variable dependiente Y explicada por una única variable predictora X con el modelo: Y=β0+β1X+ε. Obviamente β0 y β1 son desconocidos y tendrán que determinarse a partir de los datos observados en orden a minimizar el error ε. β0+β1X es la recta que define nuestro modelo, β0 es el punto en que la recta corta el eje de ordenadas, β1 es la pendiente de nuestra recta.
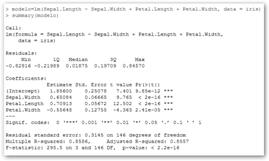
- Con la orden: modelo <- lm(Peso~Altura, data=alturaPeso) indicamos que tratamos de modelar el Peso (Y) como una función lineal de Altura (X) y se representa como V.D.~V.I.: Peso~Altura.A continuación, ejecutamos summary(modelo) para conocer la información que R nos proporciona sobre el modelo.
|
2. Observamos en la ilustración que el modelo es: Peso = -83,685 + 94,660 * Altura y que los dos coeficientes son significativos. Más concretamente, se realizan sendos test para contrastar las hipótesis nulas que β0=0 y β1=0; se demuestra que como β1 es distinto de cero la relación lineal entre Altura y Peso es significativa. Además, el coeficiente de determinación R2, es decir, la proporción de la varianza de la variable dependiente “Peso” que está explicada por la independiente Altura, es alto, aproximadamente 0.72. También, obtenemos el coeficiente de determinación ajustado o corregido: R2corregida=0.7158. |
|
|
|
|
|
|
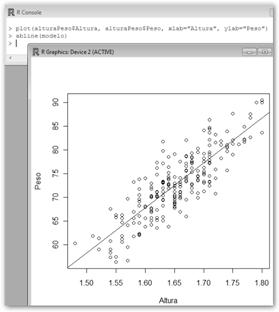
Debe observarse que la recta se ajusta bastante bien “visualmente” a la nube de puntos. |
|
|
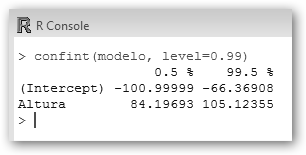
2. Podemos solicitar el intervalo de confianza de los parámetros del modelo al nivel que deseemos, en el ejemplo al 99%. |
|
|
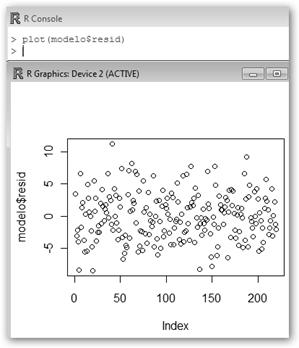
3. Finalmente, si queremos acceder a los residuos tecleamos resid(modelo) y si queremos dibujarlos plot(modelo$resid). Los coeficientes se muestran tecleando coef(modelo). 4. ¿Y cuál es el valor estimado para 1.70? Estimado <-modelo$coefficients[1] + modelo$coefficients[2] *1.70; Estimado, en este ejemplo, 77.23787. |
|
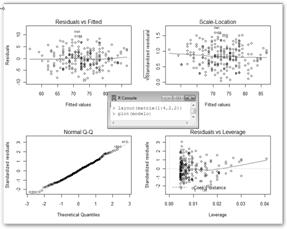
|
5. ¿Podemos fiarnos del análisis? Con layout y plot hemos obtenido cuatro gráficos: el de residuos versus los valores predichos por el modelo (deberían estar distribuidos sin ningún patrón sobre la línea horizontal), residuos estandarizados versus valores predichos, gráfico Q-Q de residuales (debe observarse que los errores residuales siguen una distribución normal) y distancias de Cook (existen valores influyentes en la estimación de los parámetros del modelo que deben ser estudiados: 5, 136 y 53). |
|
Con cook <-cooks.distance(modelo) calculamos las distancias de Cook y con valoresSignificativos<-cook>1; valoresSignificativos obtenemos aquellos que son significativos, debería resultar que para todas las observaciones obtenemos FALSE, es decir, no hay observaciones anómalas. Por último, veremos un análisis de regresión múltiple, es decir, tenemos una variable dependiente (Y) y dos variables predictoras o independientes (X1, X2). La variable dependiente Y está explicada por las variables predictoras X1 y X2 con el modelo: Y=β0+β1X1+ β2X2+ε. |
|
|
Obtenemos que el modelo es: Y = -50,3588 + 0,6712 * Air.Flow + 1,2954 * Water.Temp, que los coeficientes son significativos y que el coeficiente de determinación R2 es alto 0,90. |
Observa los tres pasos: 1. Leemos del archivo de datos: datos <-read.table("C:/regresionMultiple.txt", header=T) o lo extraemos de una tabla (stackloss) que ya está incluida en R. 2. Indicamos nuestro modelo, por ejemplo, la pérdida de amoniaco (stack.loss) en una planta industrial se explica por el flujo del aire de la refrigeración (Air.Flow) y la temperatura del agua de entrada al sistema de refrigeración (Water.Temp): modelo = lm(stack.loss ~ Air.Flow + Water.Temp, data=stackloss). 3. Solicitamos información a R sobre nuestro modelo con: summary(modelo). |
|
Para consultar las tablas de datos que ya vienen incluidas en R escribe data() para conocerlas y help(…) para encontrar ayuda sobre una tabla específica. En el siguiente ejemplo, indicamos que podemos explicar bastante bien (R2=0.85) la longitud del sépalo de una flor con las variables: anchura del sépalo, longitud y anchura del pétalo utilizando la base de datos iris. |
Otro ejemplo es lm(Volume ~ Girth + Height, data = trees). Los factores: diámetro del árbol y su peso predicen muy bien (R2=0.95) su volumen. |
También, podríamos tener modelos “más raritos”, por ejemplo, variableDependiente ~ factor1 + I(factor^2), log(variableDependiente) ~ I (1/factor), etc. ¿Te haces una idea como de desesperado te tienes que encontrar para intentar ajustar tus datos a modelos de este tipo?
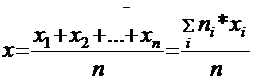



 , dejando el mismo número de datos antes y después de él una vez los hemos ordenados. En nuestro ejemplo sería: =MEDIANA( C10:C201).
, dejando el mismo número de datos antes y después de él una vez los hemos ordenados. En nuestro ejemplo sería: =MEDIANA( C10:C201). y yo ninguno y la estadística dice que nos hemos comido un pollo los dos, se soluciona con las medidas de dispersión. Utilizamos la varianza que sería el promedio de las desviaciones al cuadrado de los distintos valores a la media y la desviación típica sería su raíz cuadrada. En nuestro ejemplo son: =VAR(C10:C201) y =DESVEST(C10:C201) respectivamente.
y yo ninguno y la estadística dice que nos hemos comido un pollo los dos, se soluciona con las medidas de dispersión. Utilizamos la varianza que sería el promedio de las desviaciones al cuadrado de los distintos valores a la media y la desviación típica sería su raíz cuadrada. En nuestro ejemplo son: =VAR(C10:C201) y =DESVEST(C10:C201) respectivamente.


 resistente a los antibióticos en un
resistente a los antibióticos en un 






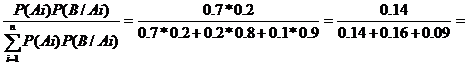 0,3589.
0,3589.



 !, como x e y son obtenidos de sendas distribuciones normales con la misma desviación típica 1, no precisamos el Test de Welch.
!, como x e y son obtenidos de sendas distribuciones normales con la misma desviación típica 1, no precisamos el Test de Welch. 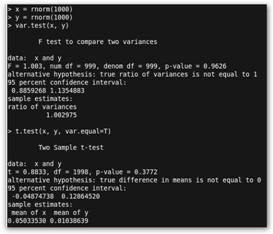

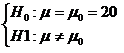


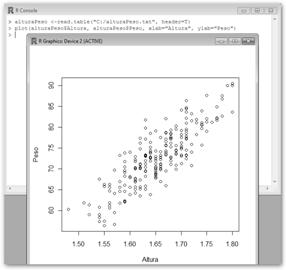
 LosTiros: plot(alturaPeso$Altura, alturaPeso$Peso, xlab="Altura", ylab="Peso").
LosTiros: plot(alturaPeso$Altura, alturaPeso$Peso, xlab="Altura", ylab="Peso").