9. Matemáticas avanzadas: ¡no es tan fiero como lo pintan!
9.1.3. Derivando que es gerundio
9.1.6. Integrales definidas y primitivas
9.2.1. Operando con números complejos
9.2.2. Representación cartesiana y polar de los números complejos
9.2.3. Jugando con las coordenadas polares
9.2.4. Representación gráfica de la suma de números complejos
9.3. Trabajando con vectores y matrices
9.4. Resolución de sistemas de ecuaciones
9.5. Editando texto científico: OpenOffice Math y el temido LaTeX
9.1. Cálculo infinitesimal.
9.1.1 Límites
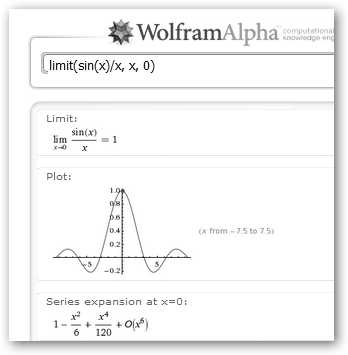
Empecemos calculando límites.
Diremosque una función f(x) tiene límite l al tender la incógnita x hacia a
(![]() ) si
) si ![]() (si para cualquier valor épsilon)
(si para cualquier valor épsilon)
![]() (existe
otro valor delta tal que) | f(x) – l | < ε si 0 <
| x –a | < δ. En cristiano paladín sería:
si quieres que los valores de la función estén en un
entorno cercano a l, digamos de radio ε, tienes que tomar los
valores x a una distancia a lo sumo δ de a, es decir, en un
entorno de radio a y radio δ.
(existe
otro valor delta tal que) | f(x) – l | < ε si 0 <
| x –a | < δ. En cristiano paladín sería:
si quieres que los valores de la función estén en un
entorno cercano a l, digamos de radio ε, tienes que tomar los
valores x a una distancia a lo sumo δ de a, es decir, en un
entorno de radio a y radio δ.
¿Cómo se calculan estos límites? Vamos a hacer distintos ejemplos en Maxima (más concretamente wxMaxima: maxima.sourceforge.net/es, lánzalo en Windows en Inicio, Todas las aplicaciones, Maxima-5.22-1, wxMaxima; en Ubuntu: Aplicaciones, Ciencia, wxMaxima) y WolframAlpha (www.wolframalpha.com).
|
|
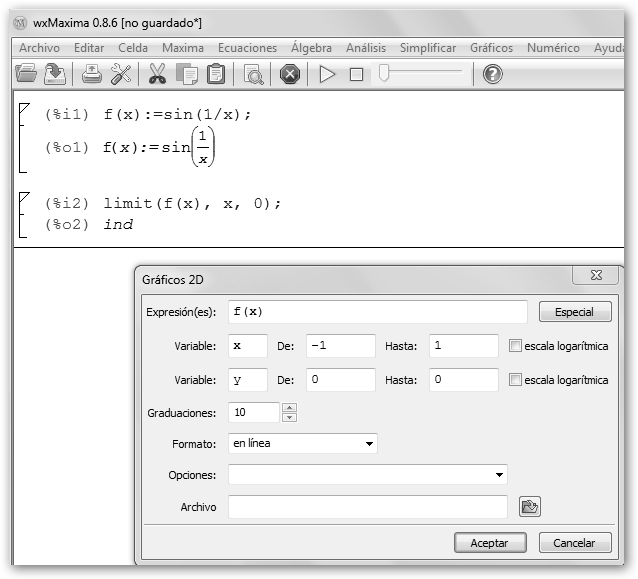
Realiza los siguientes pasos: 1. Define la función con f(x):=sin(1/x); 2. Solicita su límite cuando x tiende hacia cero: limit(f(x), x, 0). Comprueba que nos devuelve ind, indefinido. 3. Requerimos la gráfica para entender lo que está pasando desde el menú Gráficos, opción Gráficos 2D. 4. En la ventana emergente que te aparece indica que la expresión es f(x) y que quieres que grafique en el intervalo [-1, 1]. |
|
|
|
Observa la representación gráfica de nuestra función. Ésta no se asienta en ningún valor conforme se acerca a “0” sino que oscila indefinidamente en el rango [-1,1] por lo que el límite es indeterminado. Conviene también darse cuenta que podemos solicitar nosotros la representación gráfica con la orden: wxplot2d([f(x)], [x,-1,1]). |
|
|
|
En www.wolframalpha.com teclea limit(sin(1/x), x->0) y volverás a obtener un resultado similar: undefined, indefinido. Por tanto,
|
|
|
|
En ambas funciones conforme x crece, sus valores f(x) se hacen más y más grandes. ¿Y
cuál será el límite de 1/x cuando x tiende
hacia 0? Pues
|
|
|
|
||
|
|
Para conocer mejor que está pasando vamos a solicitar a Wolfram que nos muestre los límites laterales, es decir, a la derecha y a la izquierda del cero. Escribe en Wolfram: lim 1/x as x->0+. Resulta que a la derecha del cero el límite es infinito y a la izquierda es menos infinito: * 1/0.1=10, 1/0.01=100, 1 / 0.001 =1000, 1/0.0001=10000… * 1/-0.1=-10, 1/-0.01=-100, 1/- 0.001=-1000, 1/- 0.0001=-10000… La
definición formal del límite a la derecha es
|
|
|
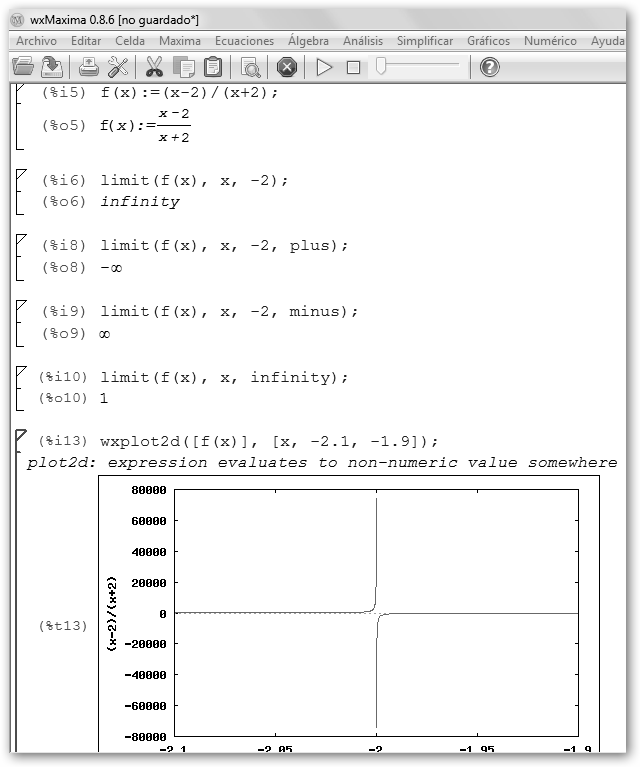
En este caso tenemos una
asíntota vertical. Más generalmente, una función tiene
una asíntota vertical si
Se ve otro ejemplo en la
figura adjunta la función
También,
solicitamos limit(f(x), x, -2, plus); es decir, el límite
por la derecha (fíjate en el último argumento plus)
|
Así se invoca los límites laterales en Maxima: limit (f(x), x, a,
plus) limit (f(x), x, a,
minus) |
|
|
Concluimos, en consecuencia, que también tiene una asíntota horizontal en la recta y=1. Si quieres verlo teclea: wxplot2d([f(x)], [x, -1000, 1000], [y, 0, 2]);.
Recuerda: una función tiene una
asíntota horizontal si sucede que
Fíjate en este
otro ejemplo.
|
|
|
9.1.2. Continuidad
Una función es continua si podemos dibujarla “sin
levantar el lápiz del papel”. Más formalmente
diríamos que una función es continua en un punto “a”
de su dominio si no sólo existe su límite en dicho
punto sino que es igual a “f(a)”, es decir, si
![]() (si
para cualquier valor épsilon)
(si
para cualquier valor épsilon)
![]() (existe
otro valor delta tal que) | f(x) –f(a) | <ε si | x
–a | < δ. Traducido sería: si quieres que los
valores de la función estén en un entorno cercano a
f(a) de radio ε, tienes que tomar los valores x a una
distancia a lo sumo δ de a, es decir, en un entorno de radio a
y radio δ. Una función se dice continua si es continua
en todos sus puntos.
(existe
otro valor delta tal que) | f(x) –f(a) | <ε si | x
–a | < δ. Traducido sería: si quieres que los
valores de la función estén en un entorno cercano a
f(a) de radio ε, tienes que tomar los valores x a una
distancia a lo sumo δ de a, es decir, en un entorno de radio a
y radio δ. Una función se dice continua si es continua
en todos sus puntos.
Veamos algunos ejemplos: 1/x que acabamos de estudiar no es continua en cero porque no está ni siquiera definida en 0. Ejemplos de funciones continuas son: x2, x-1, en realidad, cualquier polinomio, sin(x) y cos(x).
|
La función definida en trozos
1. f(0) está definido y es 0. 2. Los límites a la derecha y a la izquierda del cero existen y valen f(0). Es justo indicar que la sintaxis de WolframAlpha para trabajar con este tipo de funciones es complicada. |
|
|
¡Hay un salto
|
La función se define como {{x^2, x < 0}, {x, x >= 0}}, pero para dibujarla no sólo debemos invocar a plot sino también a Piecewise. La invocación a Maxima limit {{x^2, x<0}, {x, x>=0}} as x->0+ obtiene lo mismo. No pintan las cosas tan bien para la función:
En este caso, la función es continua tanto a la derecha de 0 como a la izquierda, es decir, en (0,+∞) y (-∞,0). |
|
Pero aunque está definida para 0 (vale 0), el límite a la izquierda es -2 y a la derecha vale 0. Luego dicha función no es continua en el punto 0. |
|
|
Comprobamos la continuidad de la función valor absoluto en Maxima. Observa que no sólo es continua en los intervalos (0,+∞) y (-∞,0) pues x y –x lo son, sino también en 0: * f(0) está definido y vale 0. * Los límites a la derecha limit(f(x), x, 0, plus) y a la izquierda limit(f(x), x, 0, minus) existen y valen f(0). |
9.1.3. Derivando que es gerundio
La derivada de una función en un punto “a” es la
velocidad de la variación de f en dicho punto. En términos
geométricos sería la pendiente de la tangente a la
función en dicho punto. Formalmente (siempre tiene que
haber alguien dando la lata ,
¿no?) una función es derivable en “a” si
este límite existe
,
¿no?) una función es derivable en “a” si
este límite existe
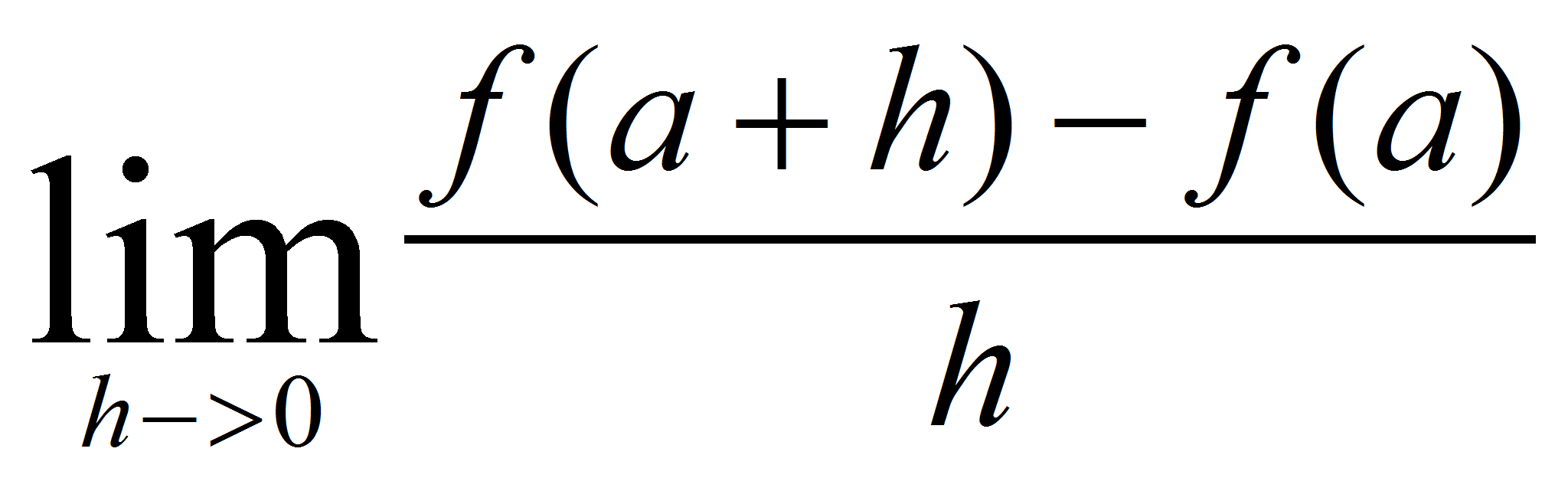 y se denomina f’(a). ¡Calculemos la derivada!
y se denomina f’(a). ¡Calculemos la derivada!
|
Para calcular la derivada de f(x) se teclea en Maxima: diff(f(x), x); Observa que hemos
calculado tres derivadas. La derivada de un polinomio es bien
conocida, si f(x)=xn entonces f’(x)=nxn-1y
también hacemos uso de las fórmulas (f(x)
En la segunda derivación, hacemos uso de la derivación de funciones compuestas. Si nuestra función a derivar es f(g(x)) su derivada es f’(g(x)).g’(x). |
|
|
Recuerda que la derivada de la función coseno es –seno. Finalmente, la tercer derivada se hace uso de la fórmula para cocientes (f/g)’ y de ratsimp(%) para simplificar la expresión resultante, en este caso:
|
|
|
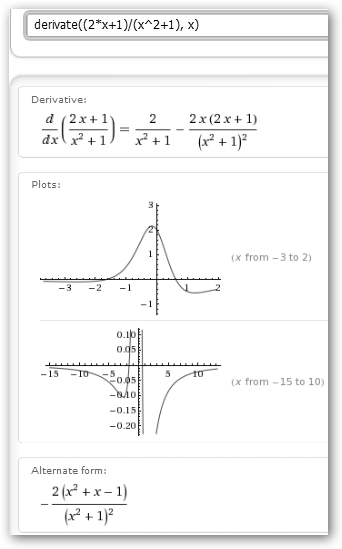
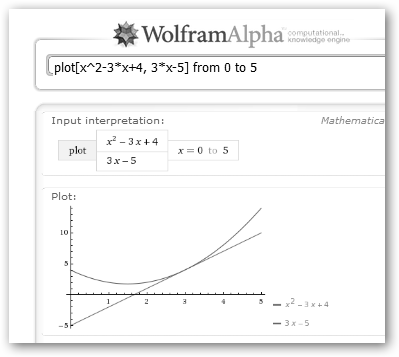
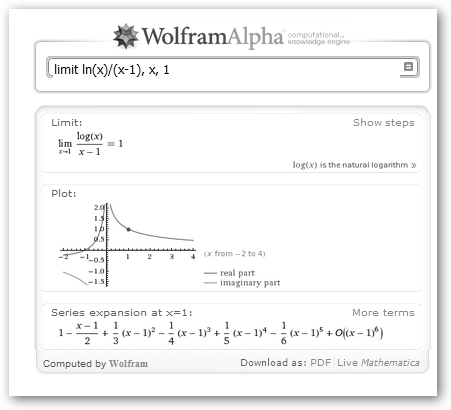
Realizamos la misma operación en WolframAlpha. En este caso, aplicamos la sintaxis derivate(función, variable). Si haces clic en Show steps en la sección Derivate en la esquina superior derecha (no aparece en la figura), puedes ver paso a paso como se aplica la fórmula del cociente. Dijimos que la derivada de una función en el punto “a” es la pendiente de la tangente a la función en dicho punto. Sea la parábola x2-3x+4, realiza los siguientes pasos: 1. Calcula la derivada: f’(x)=2*x-3. 2. Más calculitos: f’(3)=2*3-3=3 y f(3)=32-3*3+4=4. 3. La recta tangente en 3 tiene como ecuación y=f’(3)(x-3)+f(3), es decir, como pendiente f’(3) y pasa por (3, f(3)). 4. Resolvamos: y= f’(3)(x-3)+f(3)=3(x-3)+4=3x-9+4=3x-5. |
|
|
5. Dibujemos finalmente en Wolfram la parábola x2-3x+4 y su recta tangente en 3: 3x-5 en el intervalo [0, 5] para verlo mejor. |
|
9.1.4. Regla de l’Hôpital
En pocas palabras, lo
que nos dice es que si dos funciones f y g son diferenciables en a,
se anulan en a (f(a) = g(a) = 0) y existe el límite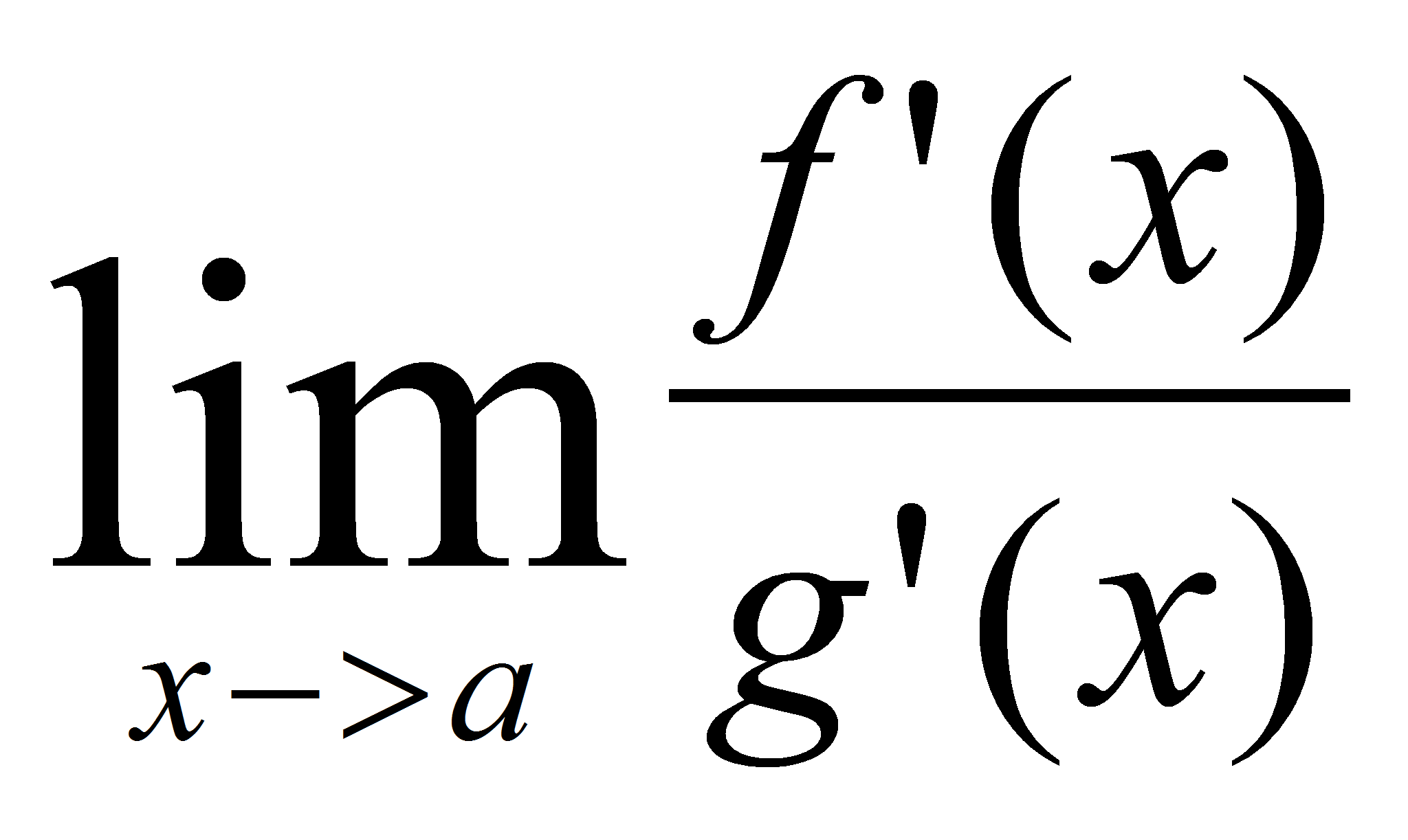 entonces
existe el límite
entonces
existe el límite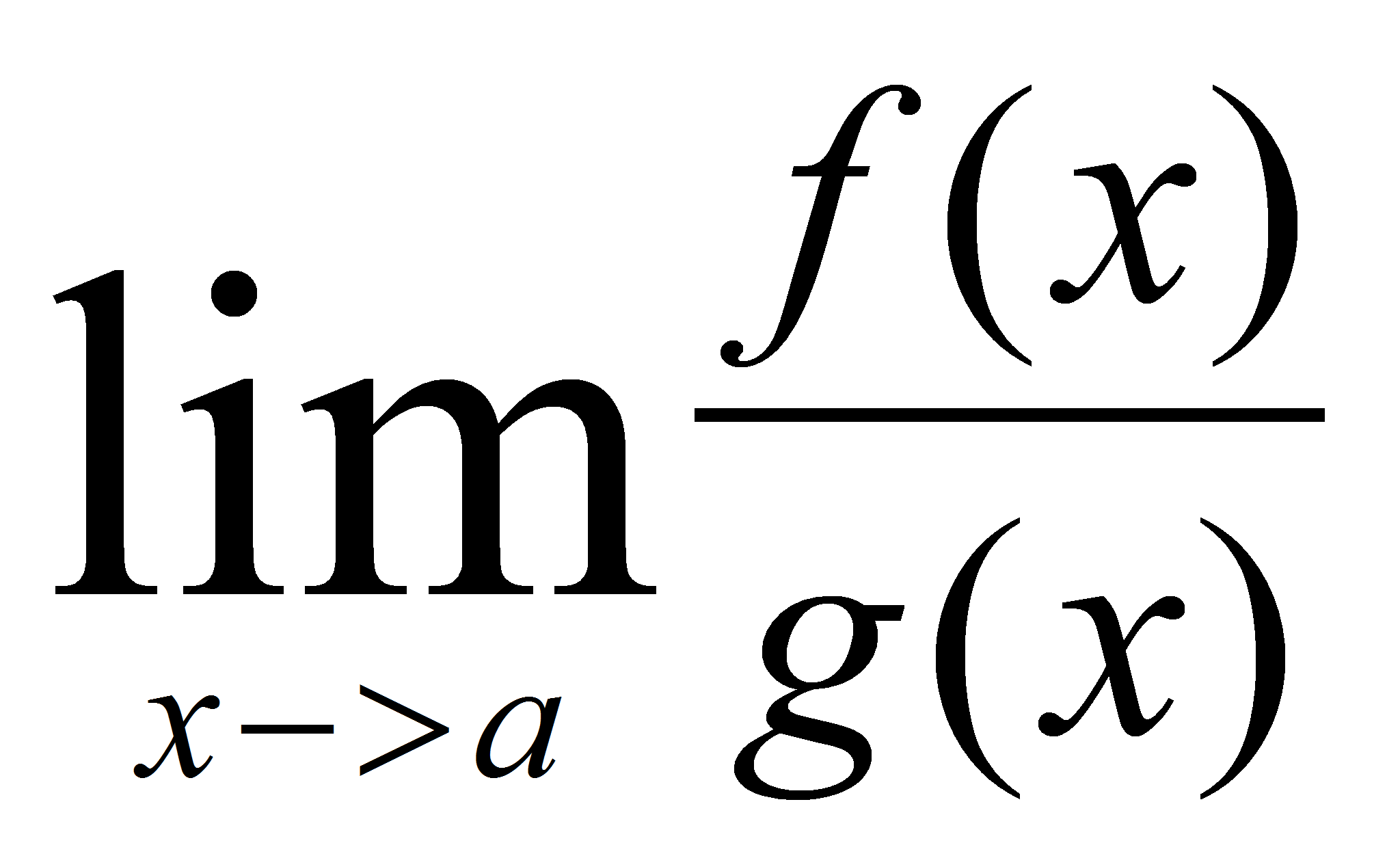 y es igual al primero, es decir:
y es igual al primero, es decir:
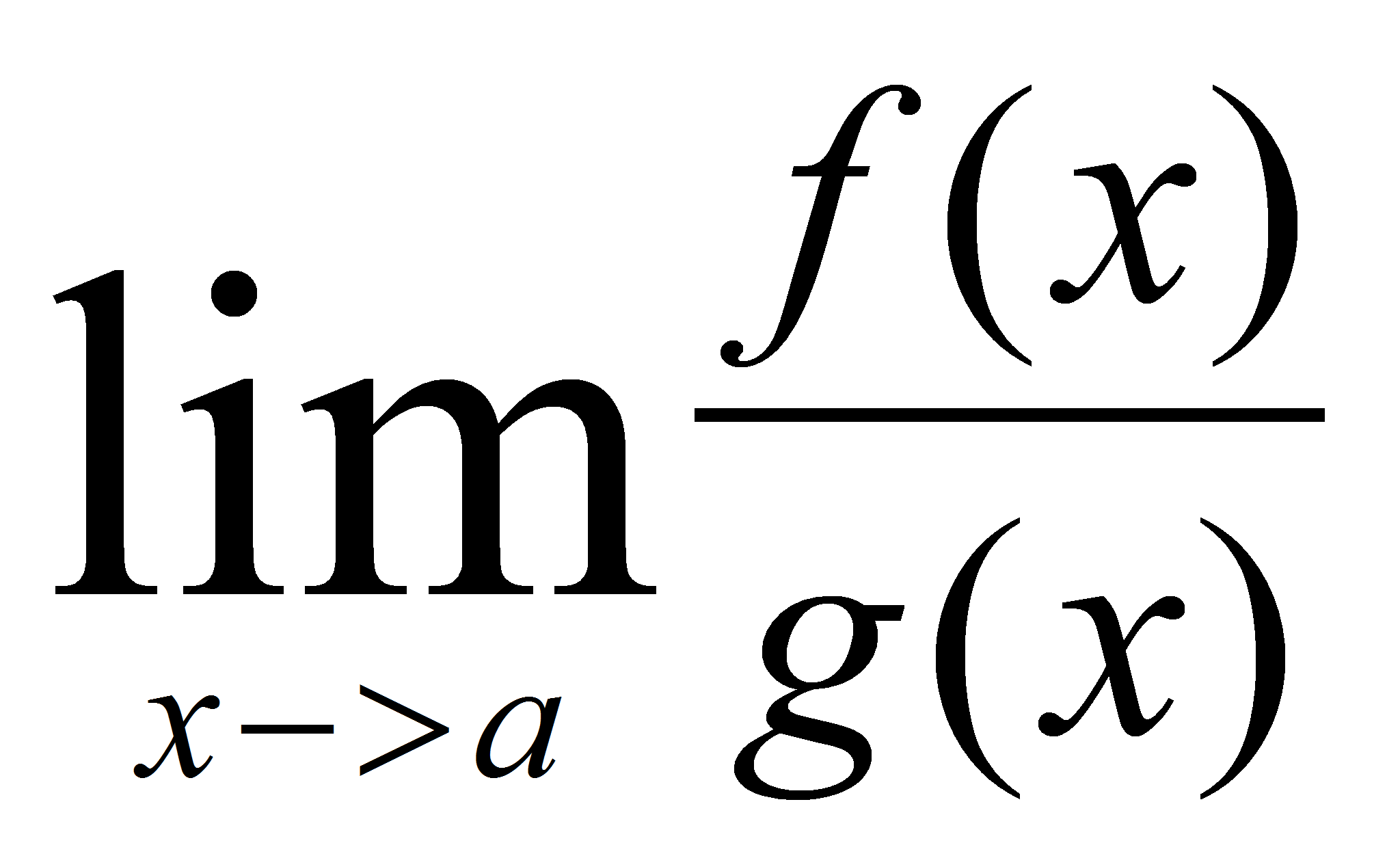 =
=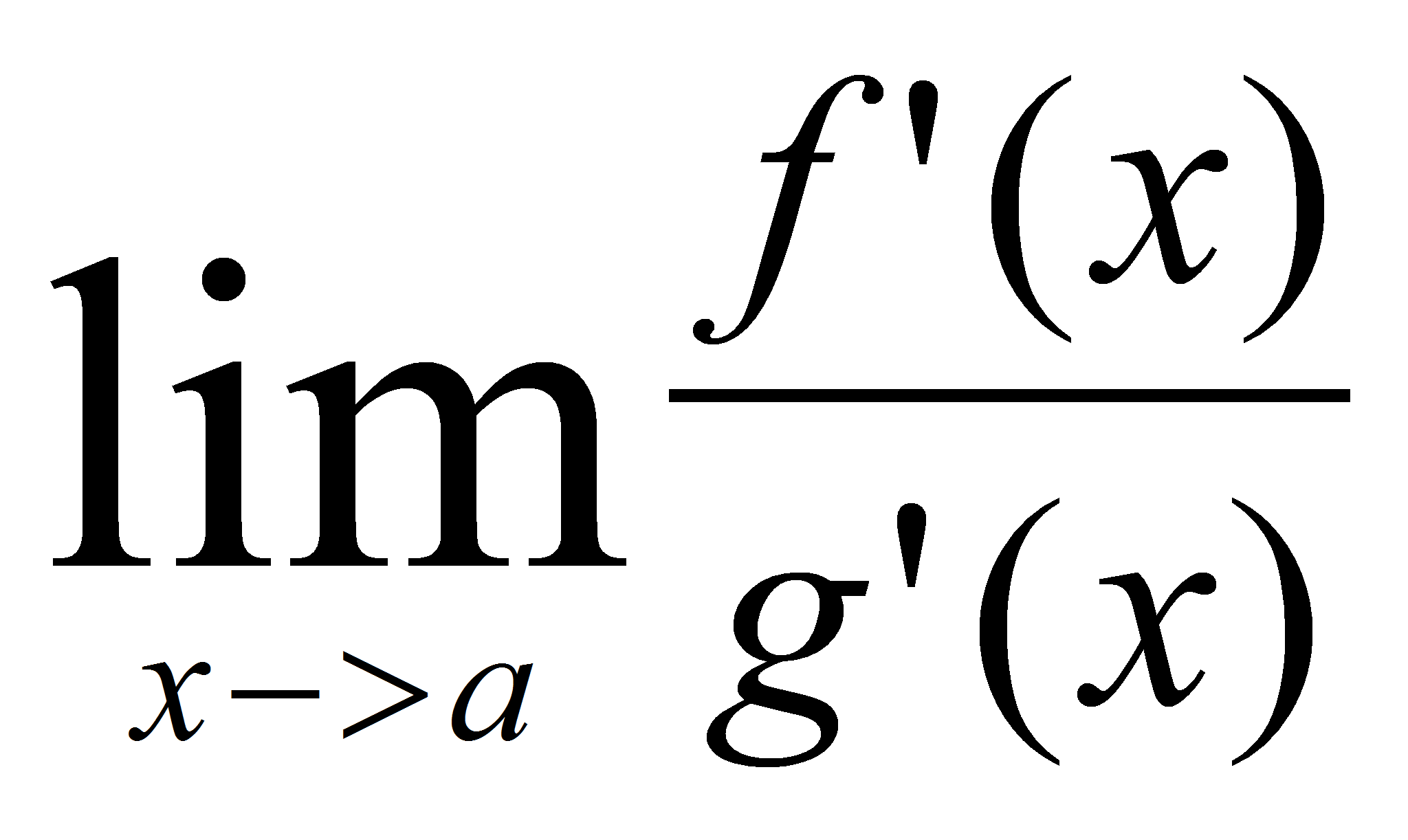 . Por ejemplo
. Por ejemplo
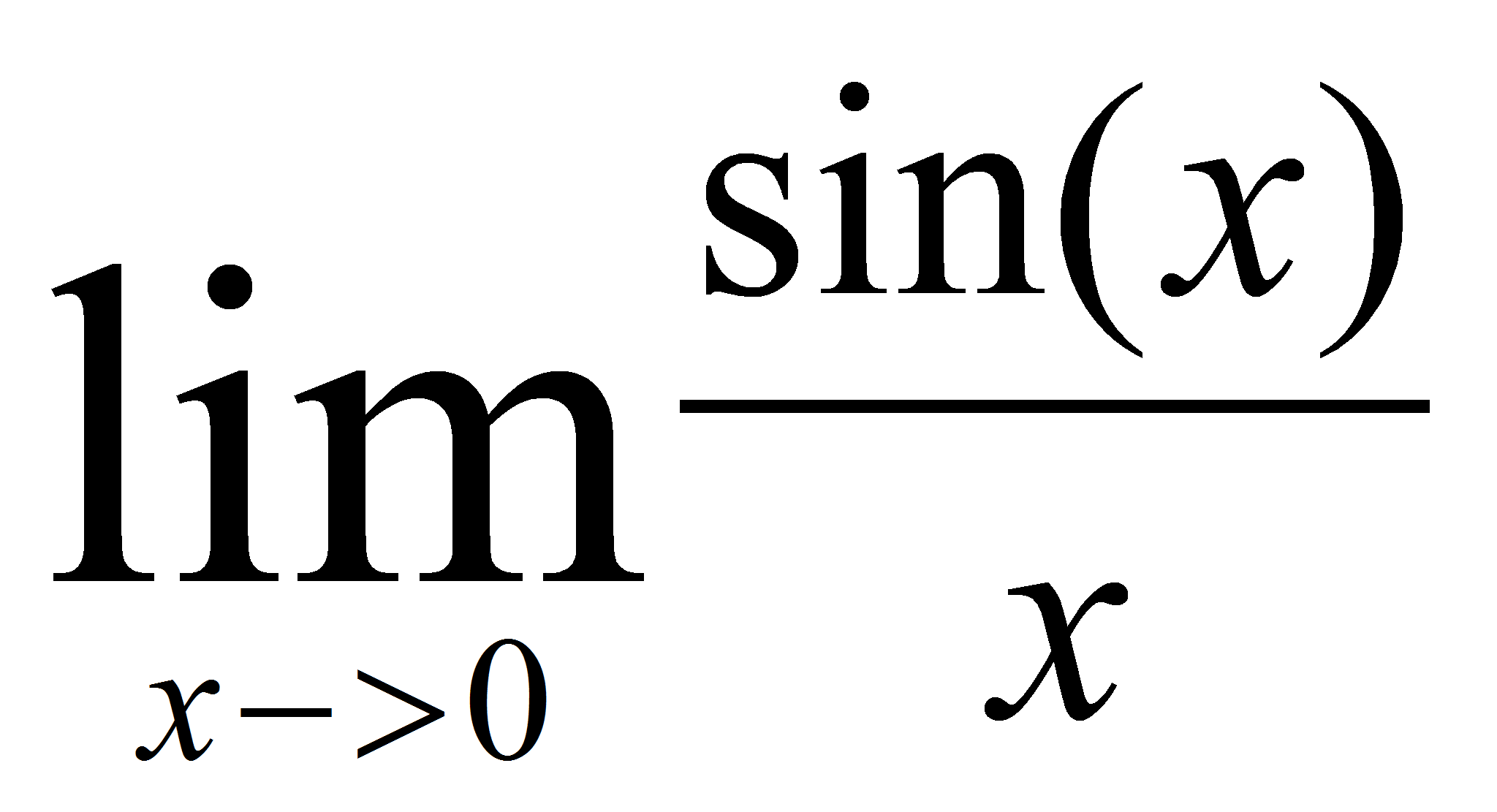 , sin(0)=0, y el
, sin(0)=0, y el
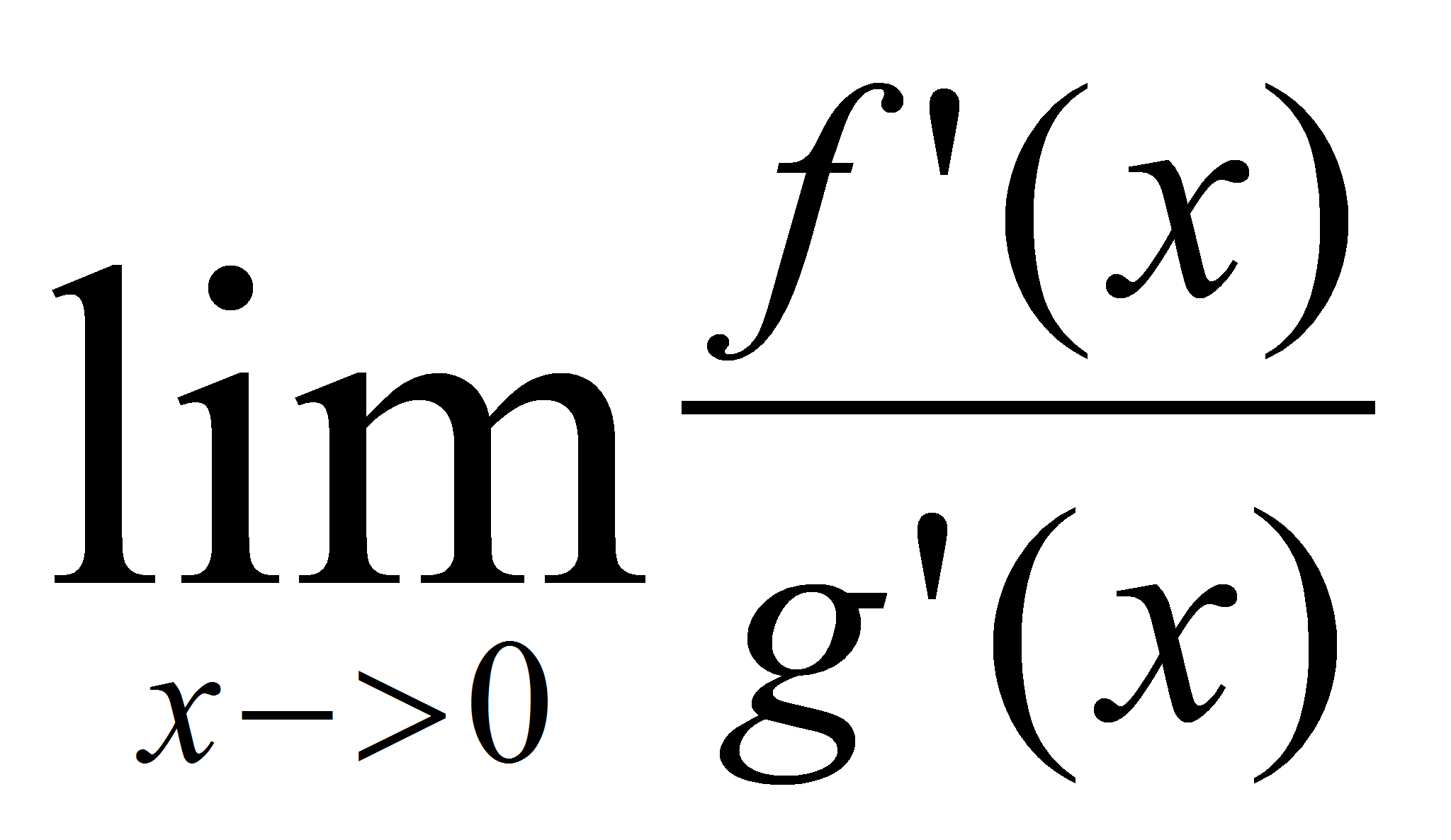 =
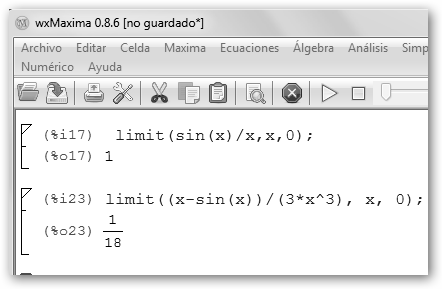
=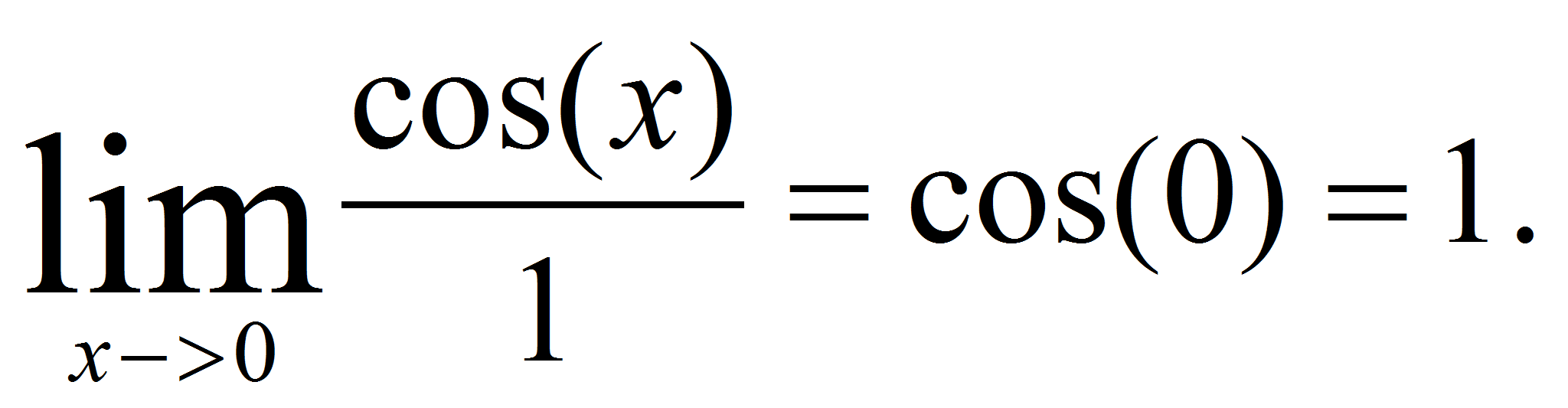 Veamos lo que WolframAlpha y Maxima dicen al respecto.
Veamos lo que WolframAlpha y Maxima dicen al respecto.
|
|
|
|
Observa que hemos aplicamos la regla varias veces.
|
|
9.1.5. Cálculo de series
|
Una serie es la suma
infinita de los términos de una sucesión:
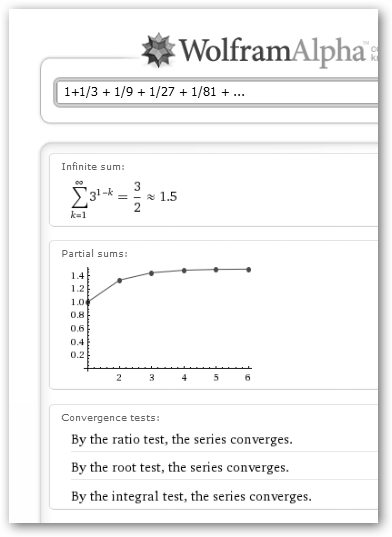
En WolframAlpha escribimos 1+1/3 + 1/9 + 1/27 + 1/81 + ... y nos dice que la serie converge y que vale 1.5. En realidad, se
trata de una serie geométrica
|
|
|
En Maxima definimos primero los términos de la sucesión o término general: a[n]:=1/(3^n); A continuación, solicitamos la serie sum(a[i], i, 0, inf) y con simpsum lo simplificamos. Teclea también: (1) a[n]:=1/(2^n);
(2) sum(a[i], i, 0, inf), simpsum; y obtendrás 2 (es
otra serie geométrica:
|
|
|
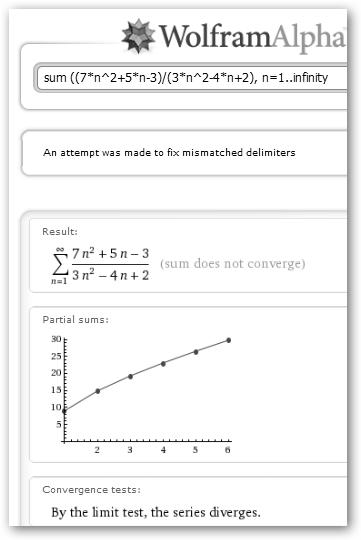
Podemos también calcular la suma n-ésima de la serie, observa los resultados de 0, 1, 2, … n y 1, 3, 5,… 2n-1 respectivamente. |
|
|
Fíjate que te lo está indicando: By the limit test, the series diverges, por el test del límite la serie diverge. |
Prueba ahora en
Wolfram: sum(1/(n*(n+1)), n=1..infinity y sum(1/(n^2),
n=1..infinity y verás que convergen a 1 y a
Sin embargo, no
siempre el mundo es de color de rosa.
Una condición necesaria pero no suficiente para que la serie
En el caso que nos ocupa
la serie es divergente |
9.1.6. Integrales definidas y primitivas.
|
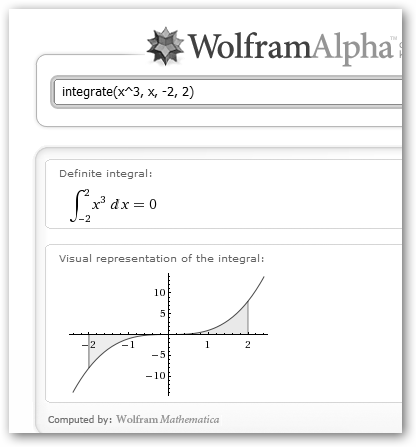
Solicitamos el cálculo de la integral tanto en WolframApha como en Maxima, las sintaxis son bastantes similares: integrate(función, variable). Observa que como la primitiva F de una función continua f verifica que F’ es f, podemos comprobar que nuestros resultados son correctos. |
|
|
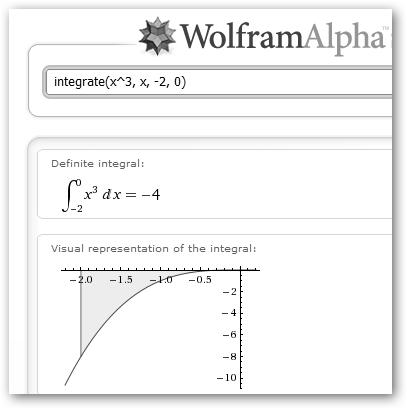
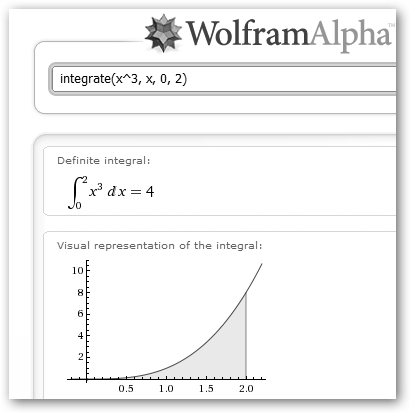
En el caso de las integrales definidas, la sintaxis es un poco diferente sería: integrate(función, variable, valor_mínimo, valor_máximo). Muy interesante es el resultado que nos muestra WolframAlpha. En este caso es una representación visual de la integral, el área limitada por la gráfica de la función. ¡Pero ojo!, cuando la función toma valores positivos el área toma signo positivo y su signo será negativo en caso contrario, de ahí que la integral definida de x3 entre [-2, 2] sea 0. |
|
|
|
|
|
Comprobémoslo con algunos calculillos. Recuerda que si F es
la primitiva de nuestra integral, se verifica que
|
|
Haz otras pruebas: integrate(sin(x)*cos(x), x) devuelve -1/2*cos2(x); integrate(exp(x)/(1+exp(x)), x); devuelve log(ex+1); integrate((2*x-5)*sin(x), x); da 2sin(x)+(5-2x)cos(x), integrate(1/x, x, 1, %e) da 1 en Maxima (observa el uso del porcentaje %e) en Wolfram quítalo; integrate(sin(x), x, 0, %pi); da 2,…
9.1.7. Series de Taylor.
|
La idea es bien sencilla: aproximar una función mediante un polinomio de grado prefijado en el entorno de un punto “a” e incluso conocer el orden de magnitud del error que sabemos que estamos cometiendo. Necesitamos que la función sea derivable infinitamente (las derivadas de sus derivadas sean derivables …) en un entorno de “a”. Entonces podemos expresar nuestra función de la siguiente fórmula: f(x)=
En el caso de la exponencial como (ex)’= exy e0=1, se obtiene: ex=
|
En la figura de la izquierda se han dibujado tanto ex como su desarrollo de Taylor. En wxMaxima los mismos resultados se obtendrían con: taylor(exp(x), x, 0, 6) o taylor(tan(x), x, 0, 6); en este caso, la sintaxis sería taylor(función, variable, a, orden). |
9.2. Cálculo complejo.
9.2.1. Operando con números complejos.
Un número complejo es un par ordenado (a, b) donde a y b son números reales. Se representa como a + bi donde i es la raíz de -1.
|
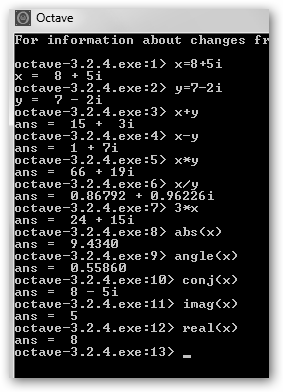
Trabajemos con complejos en Octave (www.gnu.org/software/octave/). En Windows arráncalo desde Inicio, Todos los programas, GNU Octave 3.2.4, Octave. Realiza lo siguiente: 1. Definimos dos complejos x e y: x=8+5i, y=7-2i. 2. Realizamos la suma, resta, multiplicación, división y multiplicación por escalar: x+y, x-y, x*y, x/y, 3*x. Por ejemplo x + y= (8+7)+(5-2)i=15+3i. 3. Solicitamos el módulo
de x: abs(x)= 4. Y también
el argumento: angle(x)=
5. Pedimos finalmente el conjugado (conj(x)=Real-Imag i), la parte imaginaria (imag(x)) y la parte real (real(x)).
|
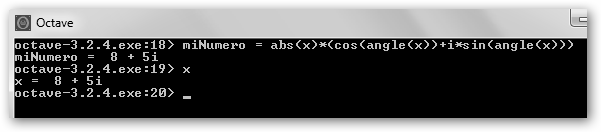
Para facilitar la comprensión, expresamos x como Real + Imag i. Por tanto x podemos expresarlo: * En forma polar o exponencial: 9.4340 ei (0.58860+2*Pi*n) siendo n un entero cualquiera. * Trigonométrica: 9.4340 * (cos(0.58860+2*Pi*n)+i*sin(0.58860+2*Pi*n). |
||
9.2.2. Representación cartesiana y polar de los números complejos.
|
|
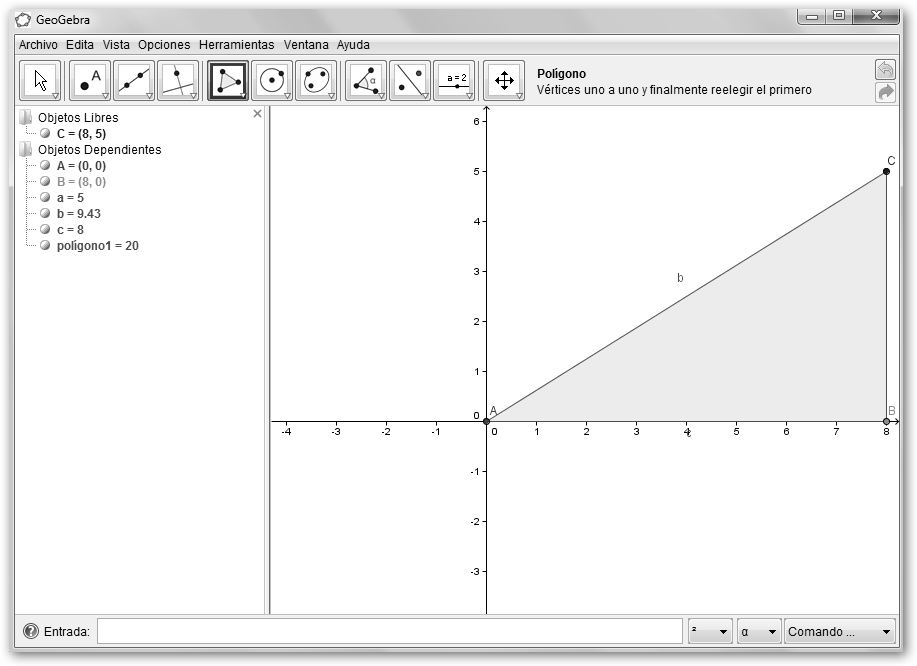
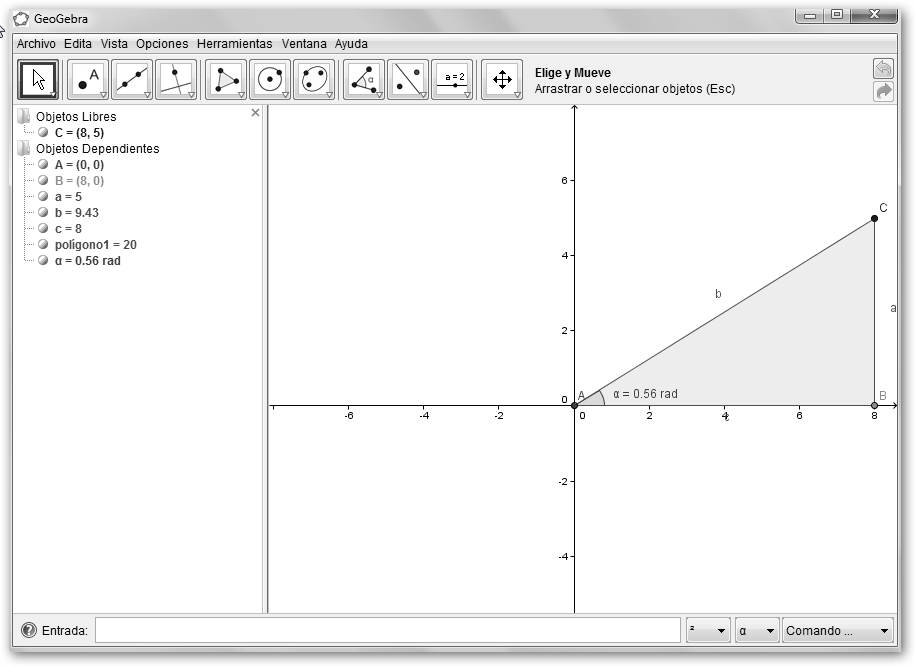
Ahora vamos a representar el número complejo x=8+5i en GeoGebra. Creamos un triángulo en GeoGebra. Primero haremos uso de la herramienta Polígono haciendo clic sucesivamente en A(0,0), B(8,0), C(8,5) y D(0,0) o escribiendo en Entrada: A=(0,0), B=(8,0), C=(8,5), Polígono[A, B, C, A]. Observa que b=9.43 es lo que hemos denominado módulo. |
||
|
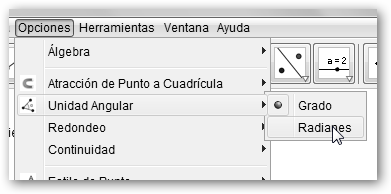
Resulta que Octave devuelve el argumento en radianes. Pasemos en Geogebra los ángulos de grados a radianes navegando por: Opciones, Unidad Angular, Radianes y comprueba el resultado final en la figura de la derecha: α=0.56 rad. |
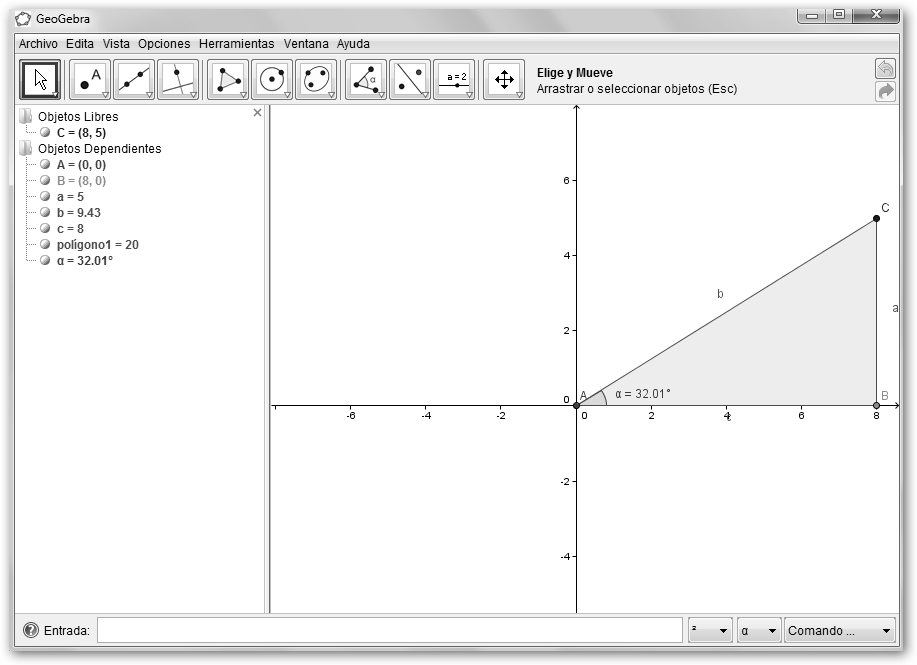
A continuación,
crearemos el ángulo haciendo uso de la herramienta Ángulo
y haciendo clic “en este orden” en B, A y C (Angulo[B, A, C]).
¿Qué nos ha salido? 32,01 y, sin embargo, habíamos dicho que el
argumento era angle(x)= 0.5586. ¡Que no cunda el pánico!
|
||
|
|
|||
|
También se puede expresar como módulo*ei*(argumento+2*Pi*n). |
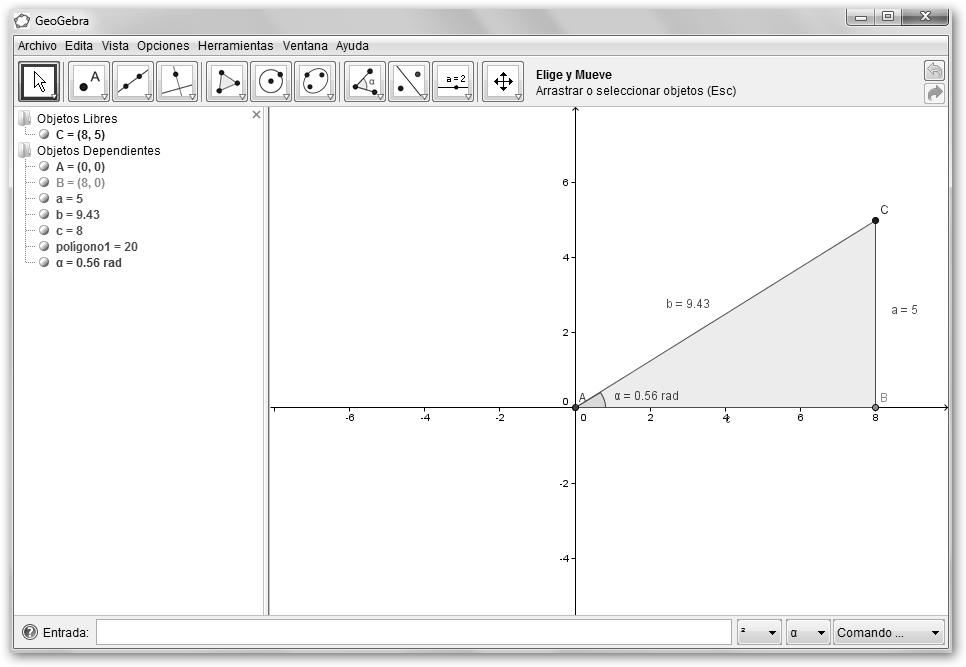
En la figura de la izquierda hemos representado finalmente el número complejo con su representación polar siendo b el módulo (haz clic sobre él, selecciona Propiedades, Muestra rótulo y elige Nombre y Valor) y α el argumento.
A continuación, recordamos que un numero complejo=módulo * (coseno(argumento)+i*seno(argumento)). |
||
|
|
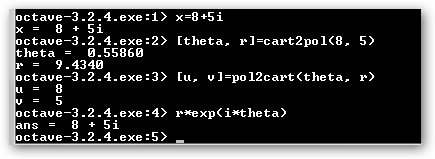
Con la función cart2pol pasamos de coordenadas cartesianas (x, y) a polares (argumento, modulo) y con pol2cart realizamos el proceso inverso. A continuación, comprobamos que las formas de expresar un complejo (polar, cartesianas) son realmente equivalentes. |
||
|
|
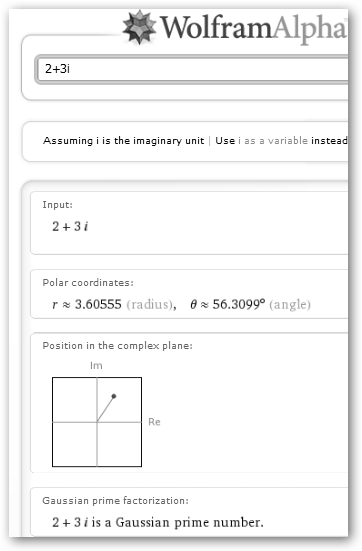
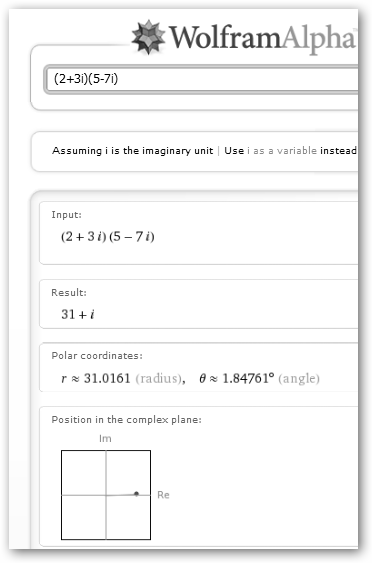
En WolframAlpha cuando introducimos un número complejo nos lo representa y nos muestra sus coordenadas polares. Además, podemos realizar con ellos las operaciones habituales. |
||
9.2.3. Jugando con las coordenadas polares
|
|
Realizamos dos apuntes más. El primero es que puedes utilizar fooplot.com para dibujar fácilmente en coordenadas polares, es decir, dibujaríamos en vez de (x, y), (theta, r(theta)). Tienes que indicarlo en el panel lateral derecho y sustituir función por Coordenadas polares. Observa, por ejemplo, que r(theta)=2 con theta oscilando en [0, 2Pi] es la ecuación de una circunferencia de radio 2. ¡Lógico!, todos los puntos tienen por definición un módulo de 2 y equidistan del origen. |
||
|
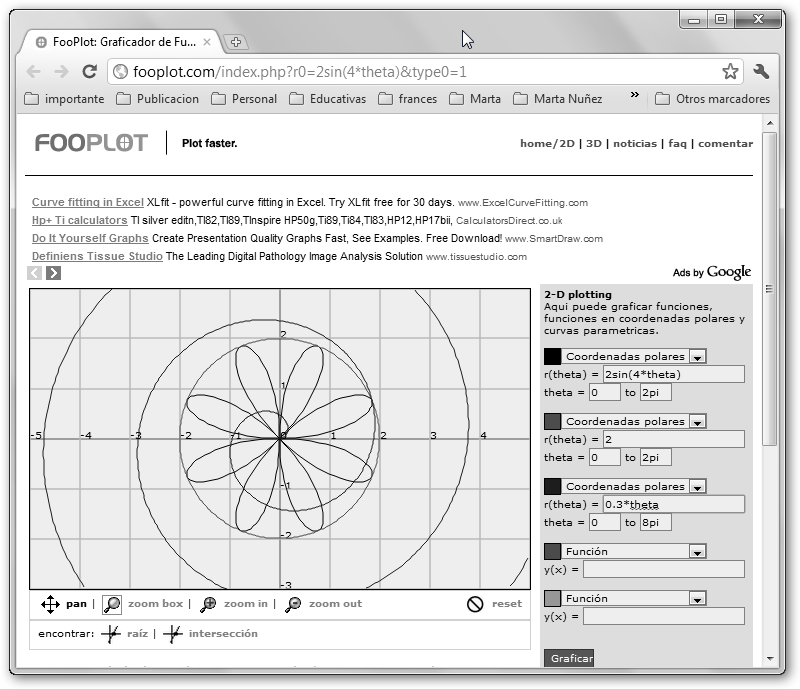
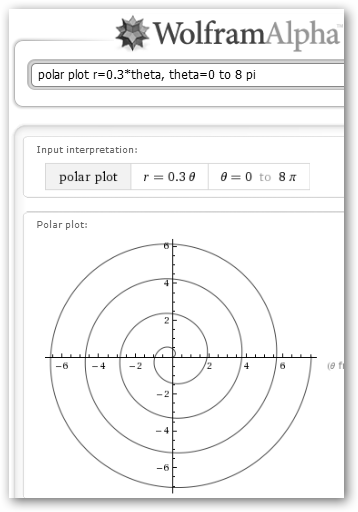
Mostramos también una rosa polar con la ecuación r(theta)=2sin(4*theta) en [0, 2Pi] y la espiral de Arquímides con r(theta)=0.3*theta en [0, 8Pi]. Modifica los valores y obtendrás figuras diferentes. |
|||
|
|
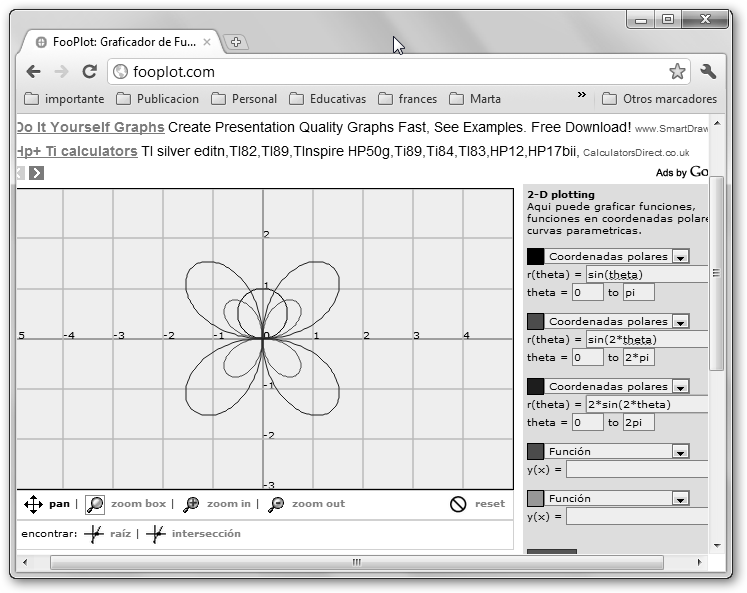
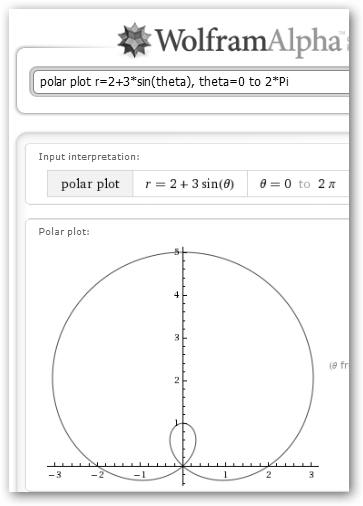
Para comprenderlo mejor observa las siguientes tres curvas: * r(theta)=sin(theta) entre [0, Pi] es simplemente un círculo de diámetro 1. Conforme theta oscila entre [0, Pi/2], r toma valores entre 0 y 1 formando la semicircunferencia de la derecha. Entre [Pi/2, Pi], r toma valores entre 1 y 0 y completa la circunferencia. * sin(2*theta) consigue obtener una flor de cuatro pétalos en [0, 2Pi] * 2*sin(2*theta) obtiene la misma flor pero con el doble de diámetro. |
||
|
Sin(2*theta) en [0, Pi/2] consigue el primer pétalo, en el tramo de theta [0, Pi/2] (el primer cuadrante) pues r llega de 0 (sin(2*0)=sin(0)=0) a 0 (sin(2*Pi/2)=0) pasando por 1 (Pi/4, sin(2*Pi/4) = sin(Pi/2) =1) y forma el pétalo. Entre [Pi/2, Pi], forma el segundo pétalo en el cuadrante inferior derecho; para el tercero precisarás el intervalo [Pi, 3Pi/2] y el pétalo se obtendrá en el cuadrante inferior izquierdo y el último que queda se forma en [3Pi/2, 2Pi]. También podemos representar en Wolfram curvas en coordenadas polares, la sintaxis sería: polar plot r=0.3*theta, theta=0 to 8 pi. |
|||
|
|
|
||
9.2.4. Representación gráfica de la suma de números complejos.
|
Alternativamente, aux1 = Vector [(0,0), a] y aux2=Vector[(0,0), b]. |
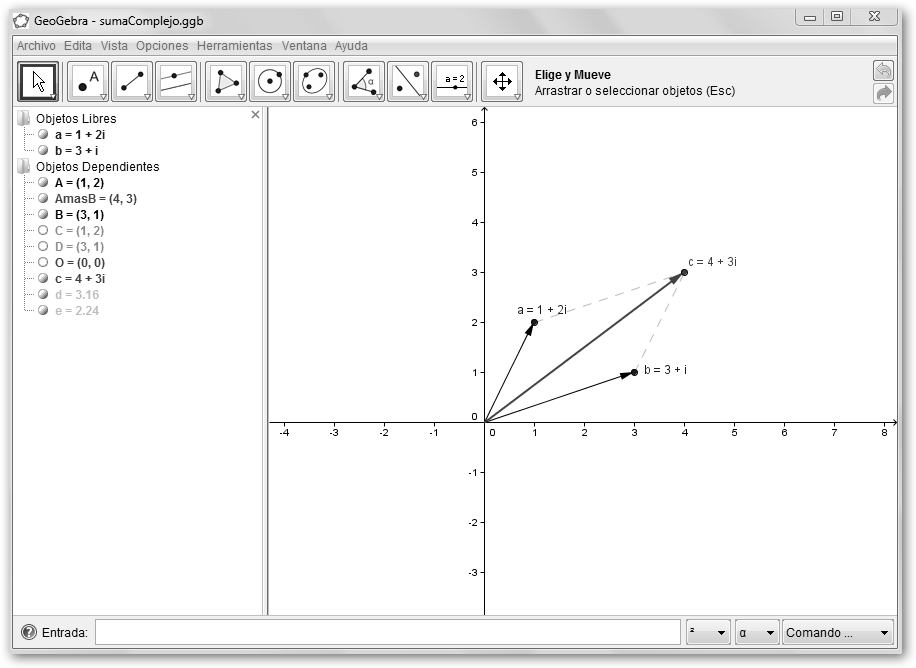
El segundo apunte es que GeoGebra puede mostrarnos gráficamente la razón de la fórmula suma de dos números complejos. Sigue los siguientes pasos: 1. Crea los puntos a y b. Puedes teclearlos directamente en la Entrada: a=1+2i, b=3+i. 2. En el menú Recta que pasa por dos puntos, selecciona la opción Vector entre dos puntos y crea dos vectores (sean aux1 y aux2) con orígenes el centro (0,0) y destinos a y b. |
||
|
3. Crea dos rectas paralelas en el menú Recta Perpendicular, la opción Recta Paralela: una que pase por “a” y sea paralela al vector aux2 y otra que pase por b y sea paralela a aux1 (llamémoslas aux3 y aux4). También se puede hacer con: aux3=Recta[a, aux2] y aux4=Recta[b, aux1]. 4. En el menú Nuevo Punto, selecciona Intersección de Dos Objetos y obtén el punto intersección de las dos rectas paralelas recién trazadas (aux3, aux4), en consola teclea c=Interseca[aux3, aux4]. Ya solo precisas crear el vector desde (0, 0) al recién creado (4, 3) con Recta que pasa por dos puntos, Vector entre dos puntos (Vector[(0,0), c]) En la figura se ha modificado algunos aspectos de forma para mejorar la apariencia. |
|||
9.3. Trabajando con vectores y matrices
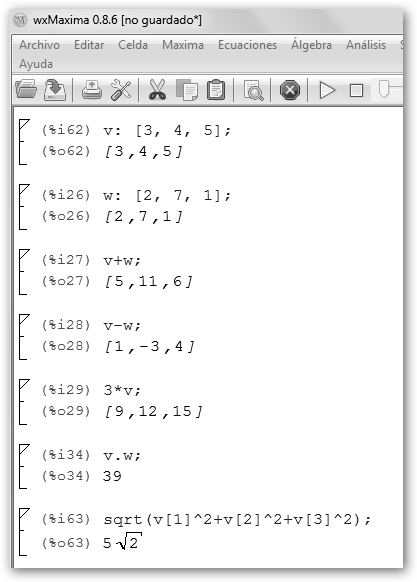
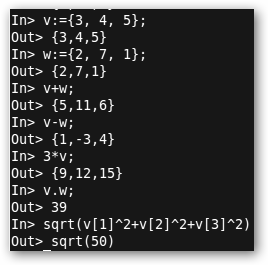
Trabajemos con vectores con wxMaxima. Primero, los definimos con miVector: [elemento1, elemento2, …]; a continuación, podemos realizar las operaciones clásicas: suma (v+w), resta(v-w), multiplicación por un escalar (3*w), producto escalar (v.w).
|
El módulo de un vector no viene implementado por defecto. Tenemos que realizarlo de la forma tradicional:
|
Para calcular el producto vectorial requerimos cargar el paquete vect con load(vect). Luego, ejecutamos v~w y express(%) o directamente: express(v~w); Para normalizar un vector cargamos el paquete eigen (load(eigen);) y escribimos unitvector(v); obtendremos [3/(5*sqrt(2)),2^(3/2)/5,1/sqrt(2)]. Finalmente, calculamos el rango de la matriz formada por los vectores v y w para conocer si son independientes o no, en este caso lo son. Escribe como ejercicio: v: [1, 2, 4]; w: [5, 10, 20]; rank(matrix(v, w)); y obtendrás 1, pues v y w son dependientes, no en vano w=5.v. |
|
|
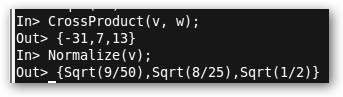
A continuación, realizamos casi lo mismo con Yacas: definición de vectores (v:={3, 4, 5}, suma (v+w), resta (v-w), multiplicación por un escalar (3*v), producto escalar (v.w), el módulo “hecho a mano”, producto vectorial (CrossProduct(v,w)) y normalización (Normalize(v)). |
|
|
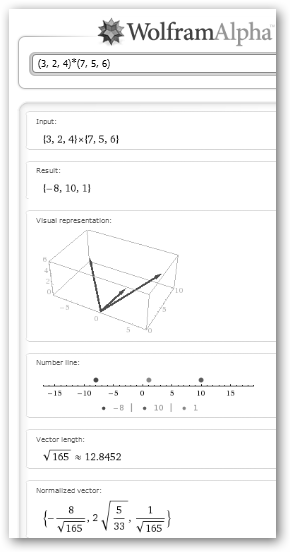
Por supuesto, todo esto lo puedes realizar si tienes una conexión “decente” a Internet desde WolframAlpha. En la figura se muestra el producto vectorial de dos vectores. Observa que también te presenta una representación visual, el módulo del vector resultante e incluso normalizado. Distintas opciones son: * vector(3, 2, 4): muestra el vector normalizado, su módulo y representación gráfica. * (3,2,4).(7,5,6): realiza el producto escalar. * 2*(3,2,4)+5(8,6,3): cálculos básicos con vectores. * norm(3, 2, 4): calcula su módulo. * MatrixRank {{3, 2, 4}, {8, 6, 3}: devuelve el rango de los dos vectores. En este caso, es 2 demostrando que se trata de vectores independientes. * Normalize(3, 2, 4): calcula el vector normalizado. |
|
Estudiemos las matrices en Octave. Se definen como se muestra en la figura a = [1, 2, 5; 3, 8, 6; 2, 5, 7], las filas precisan estar separadas por punto y coma “;”. Este sería el equivalente de lo que solemos expresar gráficamente como:
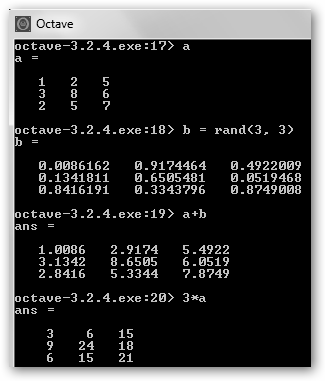
A continuación, generamos una matriz b aleatoria con tres filas y dos columnas y las multiplicamos. Observa que se precisa a(m*n)*b(n*z)=producto(m*z), donde a(m*n) expresa una matriz con “m” filas y “n” columnas. Luego, generamos otra matriz aleatoria 3*3 para mostrar la suma. Recuerda que suma[i,j]=a[i,j]+b[i,j] y que las dos matrices deben tener la misma dimensión. Finalmente, multiplicamos la matriz a por un escalar. |
|
|
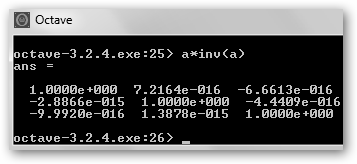
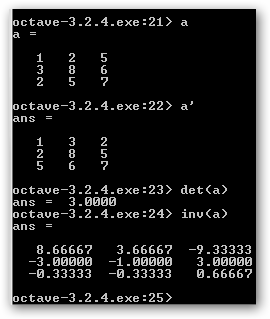
Ahora calculamos la transpuesta de una matriz con a’, es decir, la matriz que se obtiene al intercambiar sus filas y columnas, es decir, a’(i,j)=a(j,i) para todo i, j. A continuación, calculamos el determinante de la matriz con det(a) y como es distinto de cero, no es singular, podemos solicitar su inversa: inv(a). No te lleves las manos a la cabeza, si a*inv(a) no es exactamente la matriz identidad. Recuerda que trabajamos con ordenadores y estos cometen errores, pero son tan pequeñines…
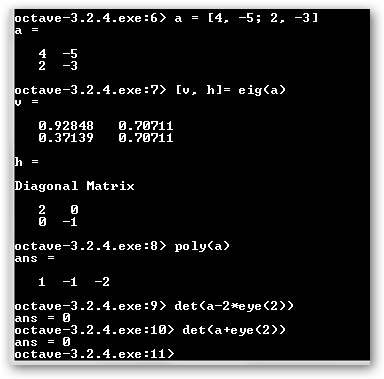
Si A es una matriz cuadrada, se dice que λ es un autovalor o valor propio si existe un vector x (es el autovector o vector propio asociado) tal que A x = λ x. Además, λ es autovalor de A si y solo si es la raíz del polinomio det(A- λ I)=0, que se denomina polinomio característico. Con eig(a) calculamos los vectores y valores propios de a. Los autovalores son: 2 y -1. En el ejemplo probamos que det(A- λ I) =det(a-2*eye(2))=det(a+1*eye(2)) =0. El polinomio característico es (λ-2)*(λ+1) = λ2- λ -2 que nos lo muestra poly(a): 1 -1 2. |
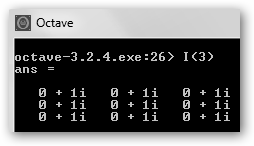
Para solicitar la matriz identidad n, basta con escribir I(n):
|
|
|
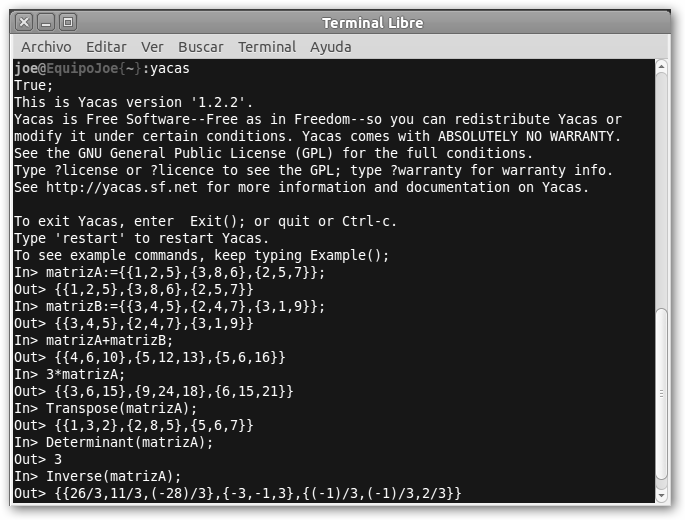
Veamos dos ilustraciones de cálculos similares con Yacas tanto en aplicación de escritorio como en la nube. |
|
|
Recuerda que hay una versión de Yacas disponible online en yacas.sourceforge.net/homepage.html en la pestaña My Yacas. Solo han
cambiado la definición de las matrices y los nombres de las
funciones transpuesta, determinante e inversa: Transpose,
Determinant e Inverse. “El mismo perro
|
|
En Wolfram Alpha también podremos trabajar cómodamente con matrices. Veamos a modo de ejemplo: la transpuesta de una matriz (Transpose[{{1, 2, 5}, {3, 8, 6}, {2, 5, 7}}], comprueba la definición diferente de la matriz); su determinante (Det[{{1, 2, 5}, {3, 8, 6}, {2, 5, 7}}]); la matriz inversa (Inverse[{{1, 2, 5}, {3, 8, 6}, {2, 5, 7}}]); suma de matrices ({{1, 2, 5}, {3, 8, 6}, {2, 5, 7}}+{{3, 4, 5}, {2, 4, 7}, {3, 1, 9}}); producto de matrices ({{1, 2, 5}, {3, 8, 6}, {2, 5, 7}}*{{3, 4, 5}, {2, 4, 7}, {3, 1, 9}}); autovalores y vectores propios (Eigenvalues[{{4, -5}, {2, -3}}], Eigenvectors[{{4, -5}, {2, -3}}]) y polinomio característico (CharacteristicPolynomial [{{4, -5}, {2, -3}}], x]); |
|
9.4. Resolución de sistemas de ecuaciones.
|
Resolvamos el siguiente sistema:
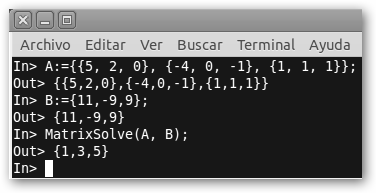
Lo hemos resuelto en Yacas, Wolfram y wxMaxima. Recuerda que todo sistema de ecuaciones lo podemos expresar de la forma A x = B donde A es la matriz de coeficientes y B es el vector de los términos independientes. En Yacas los argumentos de la función MatrixSolve son precisamente A y B. |
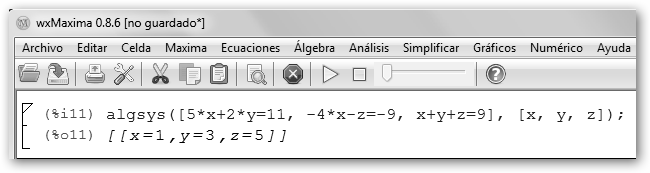
En WolframAlpha basta con separar las ecuaciones con comas y en Maxima indicar al final las incógnitas encerradas entre llaves y separadas también con comas. |
|
|
|
|
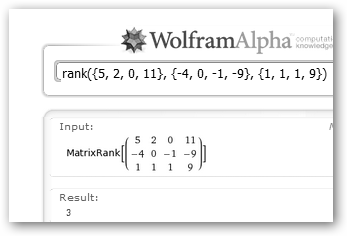
El teorema que tenemos que tener presente es el de Rouché-Fröbenius que asegura que el sistema de ecuaciones tiene solución si y solo si rango(A|B)=rango(A), donde A|B es la matriz extendida o ampliada (la matriz de coeficientes más los términos independientes). Si rango(A|B)=rango(A), el número de ecuaciones (m) es igual al número de incógnitas(n) y A es regular (rango(A)=n, es decir, det(A)≠0) el sistema tiene solución única (es un sistema determinado) que es el caso que nos ocupa: |
|
|
|
|
|
|
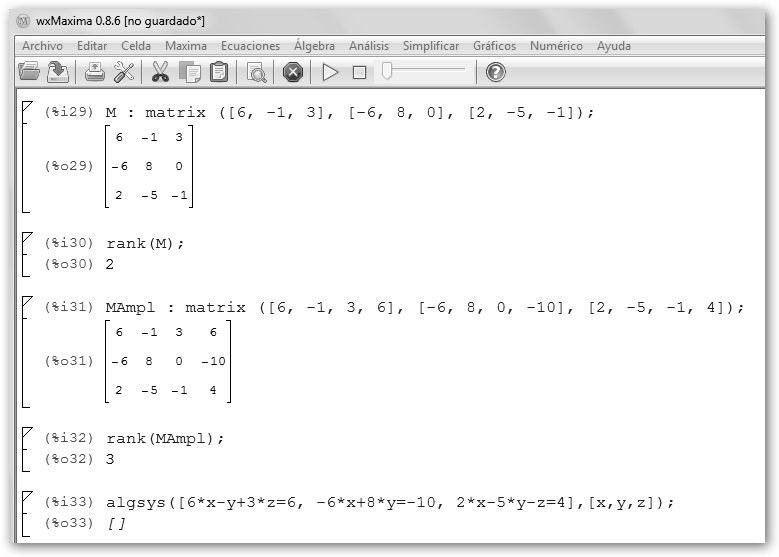
Veamos otro ejemplo con wxMaxima. El sistema de ecuaciones siguiente:
En este caso rango(A|B)=3 != rango(A)=2, luego el sistema es incompatible, no hay solución. |
|
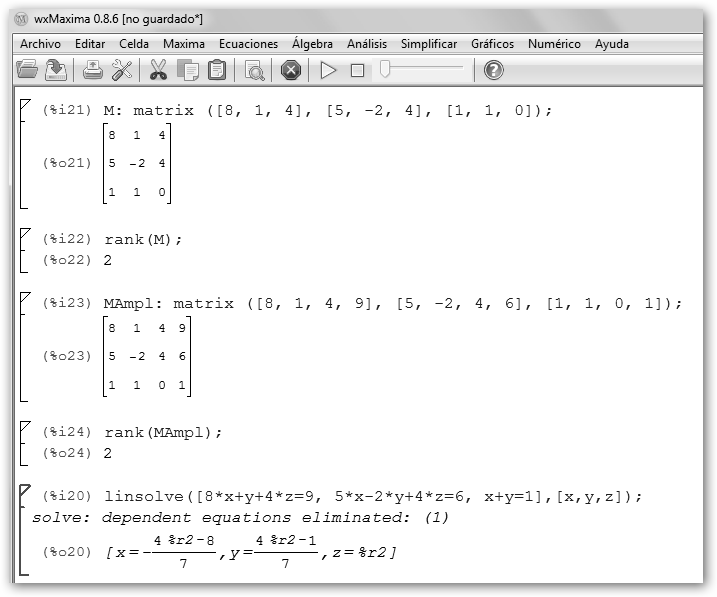
Es importante destacar que el rango de una matriz es el número de filas o columnas linealmente independientes y que en ambos programas la función se denomina rank. Solo difieren en que se definen las matrices de forma diferente. |
|
|
En el último ejemplo rango(A|B)=rango(A)=2 pero hay 3 ecuaciones para dos incógnitas, luego hay infinitas soluciones, basta con dar valores al parámetros %r2, por ejemplo 0: (8/7, -1/7, 0) cumple el sistema. |
|
9.5. Editando texto científico: OpenOffice Math y el temido LaTeX.
|
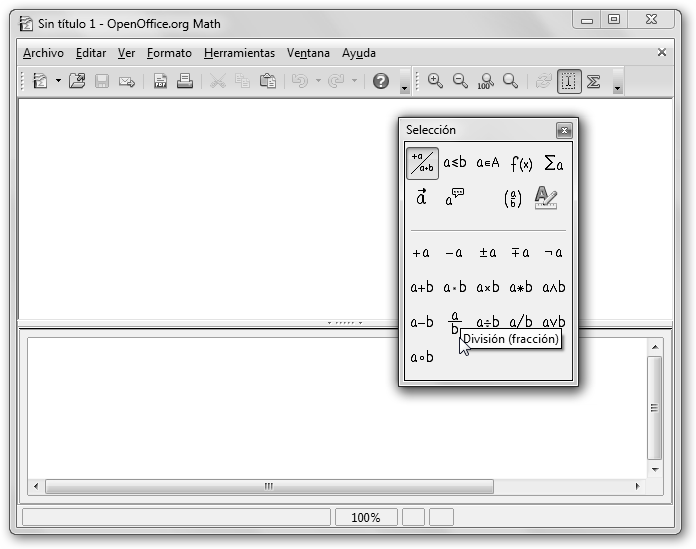
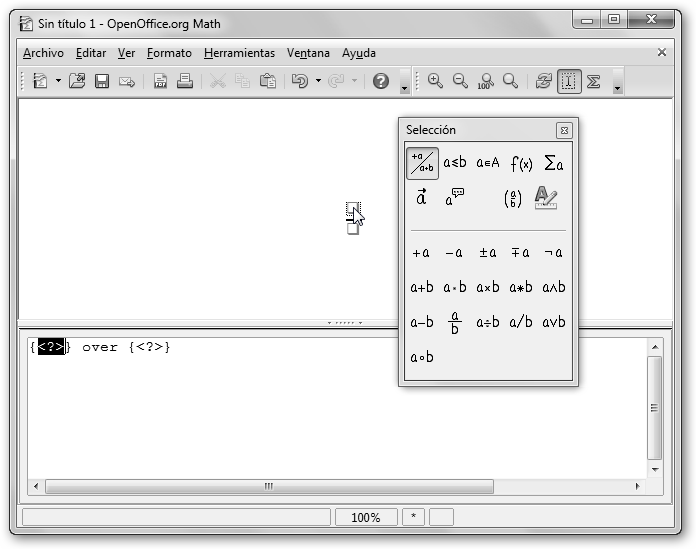
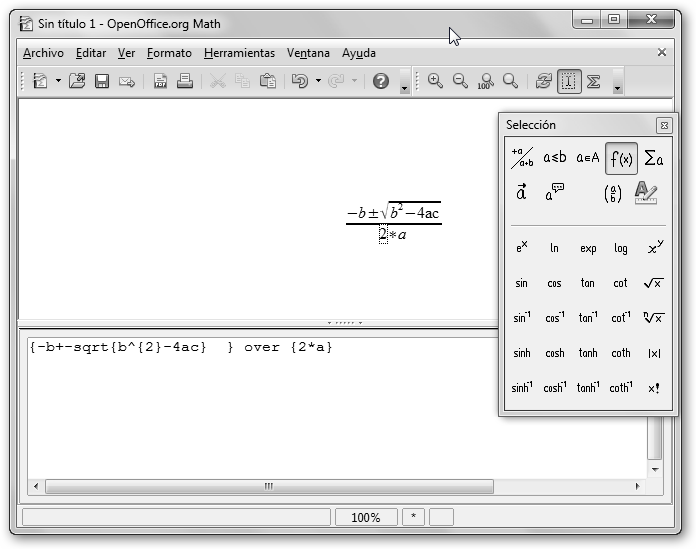
Para editar texto científico utilizaremos OpenOffice Math. Vamos a realizar una fórmula “sencillita” la solución de una ecuación de segundo grado. Sigue los siguientes pasos: 1. Descárgalo desde http://es.openoffice.org/ e inícialo en Inicio, Todos los programas, OpenOffice.org 3.2, OpenOffice Math desde Windows. 2. Fíjate en la ventana de Selección, está organizada por categorías: Operadores unarios/binarios, Relaciones, Operaciones de conjunto, etc. |
3. En particular, selecciona la División de la categoría Operadores unarios/binarios. |
|
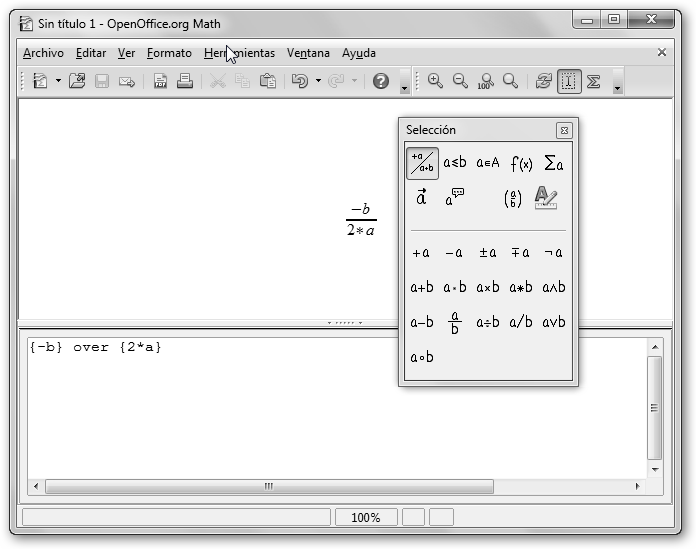
Observa podemos teclear el numerador -b desde la ventana de
selección (la superior) en los cuadraditos o en la de
comandos (inferior): sustituyendo <?> por –b y dejando las llaves
|
Es decir, es
equivalente teclear en los cuadraditos y obtener
|
|
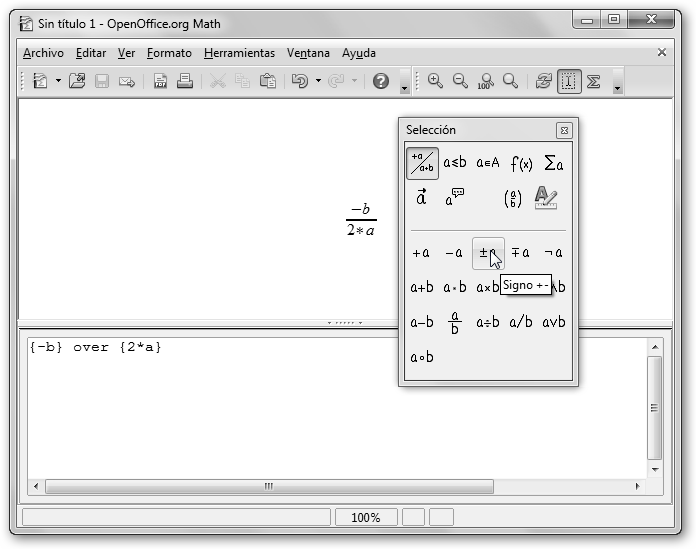
Realiza lo mismo para la opción Signo de la misma categoría Operadores unarios/binarios. |
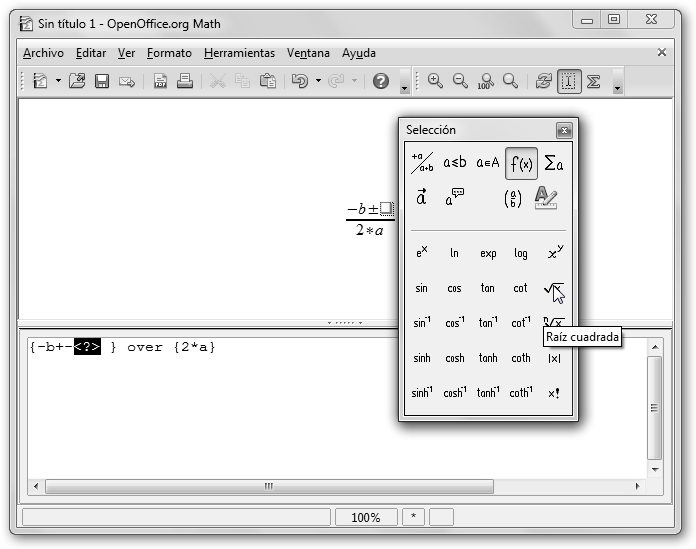
A continuación, cambiamos de categoría a la de f(x) Funciones para seleccionar la Raíz Cuadrada, equivale en comandos a sqrt{(<?>)} y acabamos la fórmula. |
|
Por si no te has dado cuenta, tendrás que utilizar la opción Potencia en Funciones para incluir en la fórmula b2. |
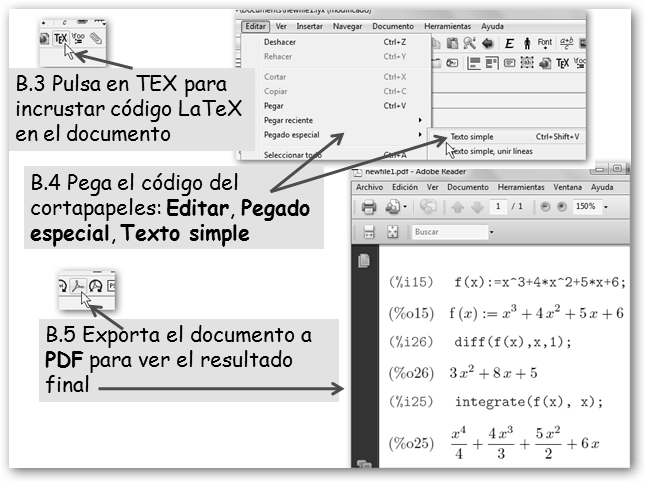
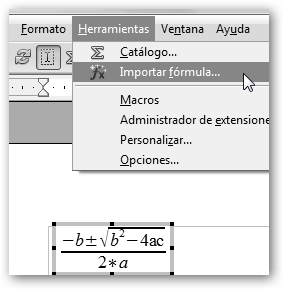
Guarda tu trabajo navegando por Archivo, Guardar, dále un nombre y sálvalo como Formula ODF (el archivo tendrá extensión .odf). También, podemos exportarla a formato PDF (Archivo, Exportar). Abre OpenOffice Writer y selecciona Insertar, Objeto, Fórmula. Ahora aparece OpenOffice Math, puedes trabajar directamente con él o importar una fórmula que hayas creado previamente desde Herramientas, Importar formula tal como se ilustra en la figura inferior. |
|
LaTeX se ha utilizado extensamente para la creación de tesis doctorales, artículos académicos, científicos y similares por la gran calidad que ofrece. Es software libre y cada día que pasa hay editores disponibles más sencillos de utilizar. |
Navega al directorio donde guardaste la fórmula, selecciónala y ya la tendrás en tu documento ofimático. Por supuesto, hay mucho más…
OpenOffice Math te permite también la inserción de
símbolos especiales y griegos (Herramientas,
Catálogo…), podemos utilizar KFormula (de la
suite Calligra en www.calligra-suite.org) y si quieres caña
* Kile: kile.sourceforge.net. * Lyx: www.lyx.org. * TexLive: www.tug.org/texlive. |
|
Observa la pantalla inicial de LyX, viene con una ayuda muy completa y sencilla, eso sí bastante extensa. En Ubuntu, Debian y derivados instala los paquetes kile, lyx y texlive-full. |
Creemos nuestro primer documento desde Archivo, Nuevo (en Archivo, Nuevo desde plantilla… vienen multitud de modelos para no empezar desde cero). |
|
Fíjate como empezamos a crear el documento directamente.
Puedes utilizar las herramientas que te proporcionan como en el
menú Insertar, Ecuación, En línea.
Al ver el fuente LaTeX (Ver, Ver fuente) podrás
comprobar que
| |
|
|
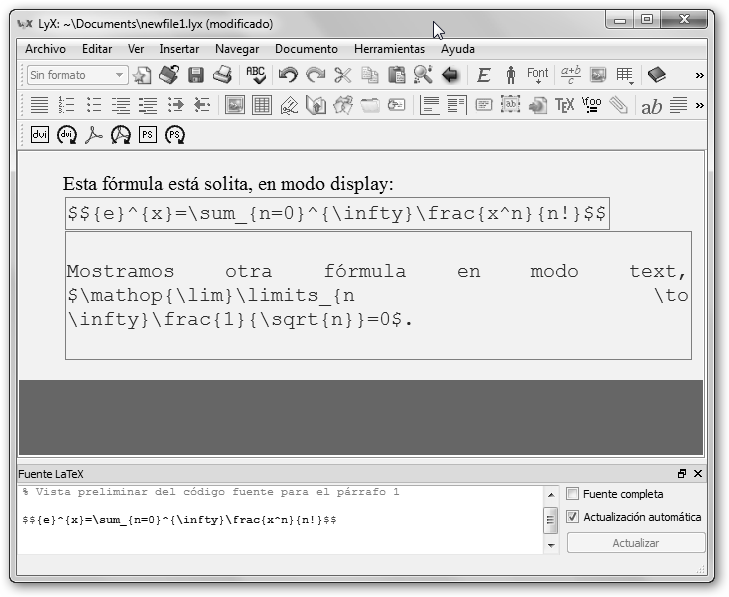
En ambos casos, debes después poner los preceptivos “$” al principio y al final de las fórmulas en tu editor LaTeX preferido en modo text, es decir, si quieres que la fórmula se muestre con el texto. |
|
|
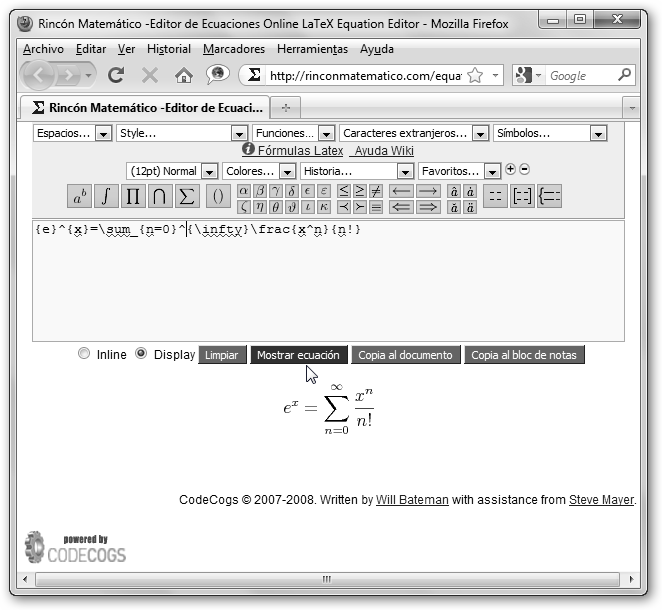
Sustituye un dólar “$” por dos “$$” si quieres que la expresión se vea en modo display. En este caso, la formula irá “tan solita” como un huérfano o Adán en el día de la madre. |
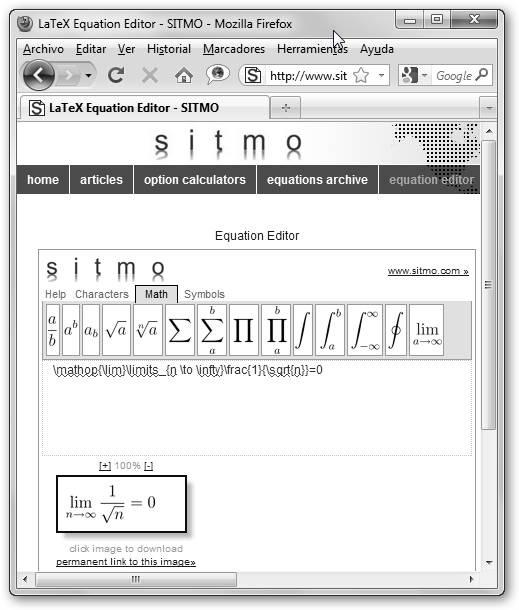
Observa el código de la serie {e}^{x}=\sum_{n=0}^{\infty}\frac{x^n}{n!} y del límite \mathop{\lim}\limits_{n \to \infty}\frac{1}{\sqrt{n}}=0.
Un soporte parcial para LaTeX lo encontramos en Google Docs, el paquete ofimático en la nube de Google con las ventajas añadidas de poder compartir documentos, publicarlos en la Web y trabajar en equipo.
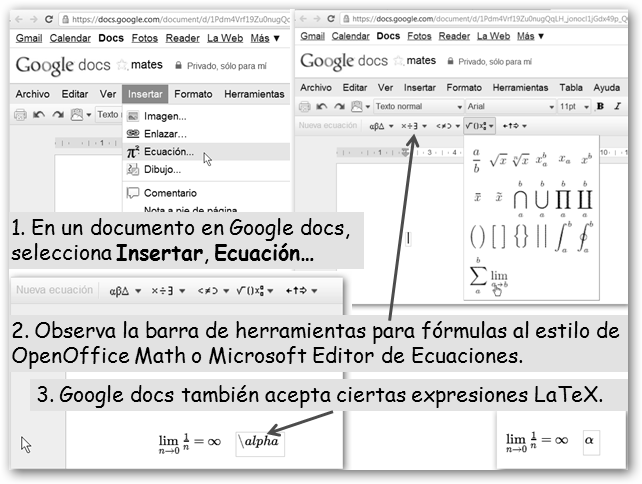
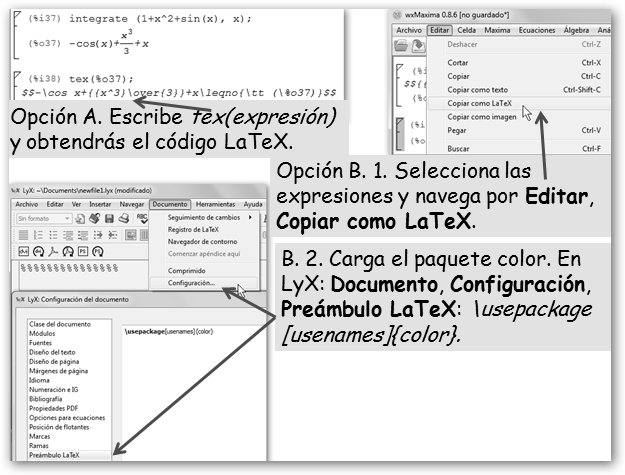
También, podemos integrar nuestro trabajo con Maxima en los documentos LaTeX:
|
|
|
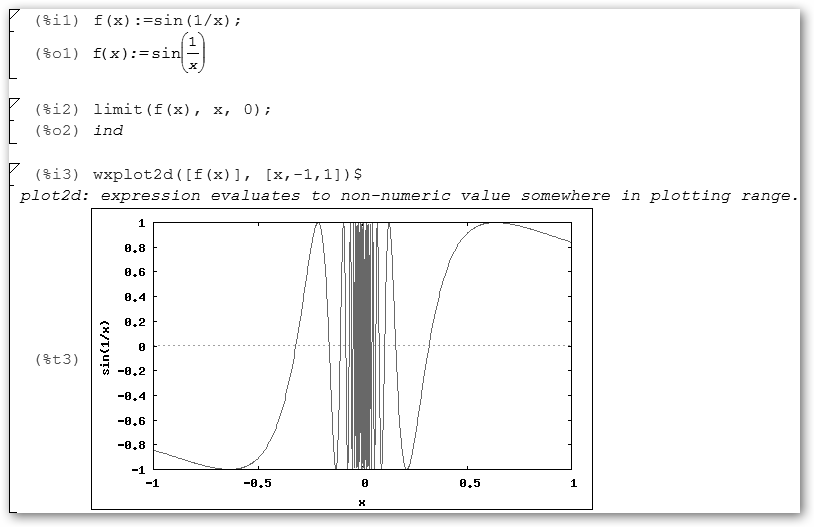
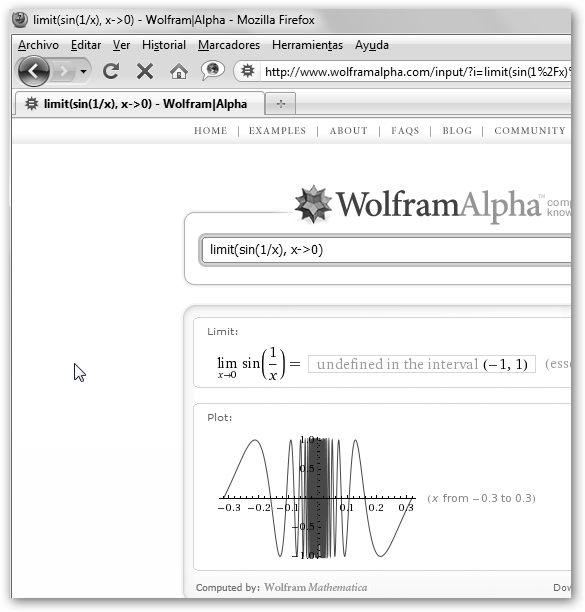
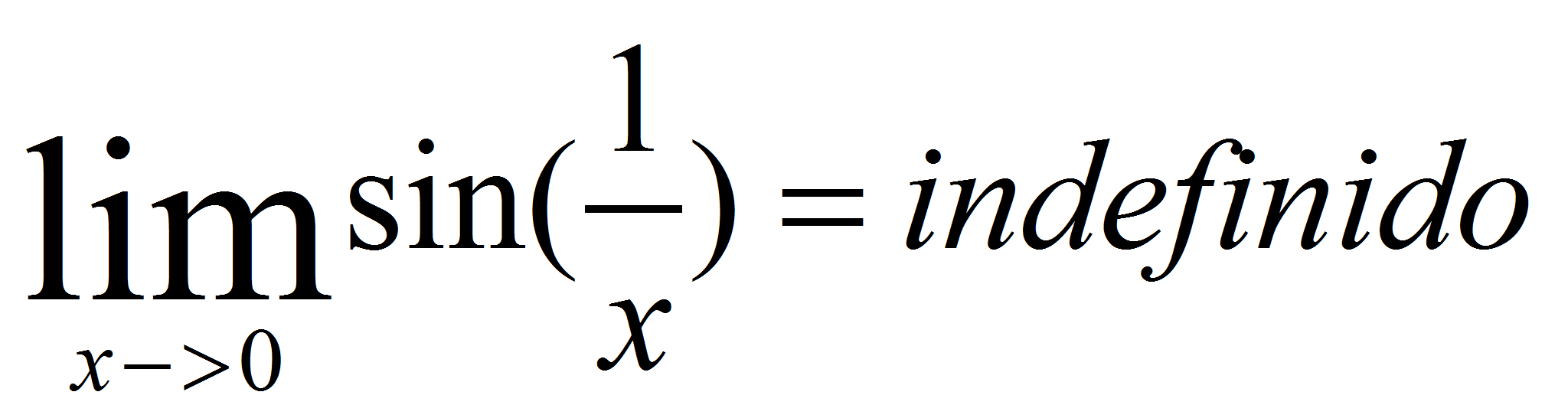 . Veamos ahora los siguientes límites:
. Veamos ahora los siguientes límites:
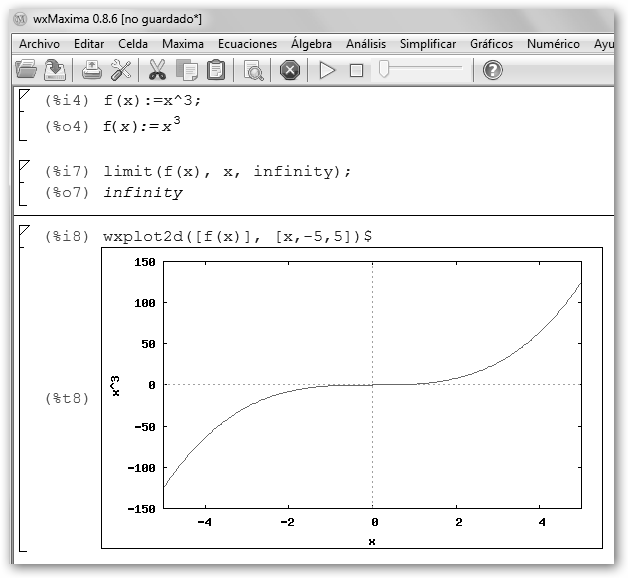

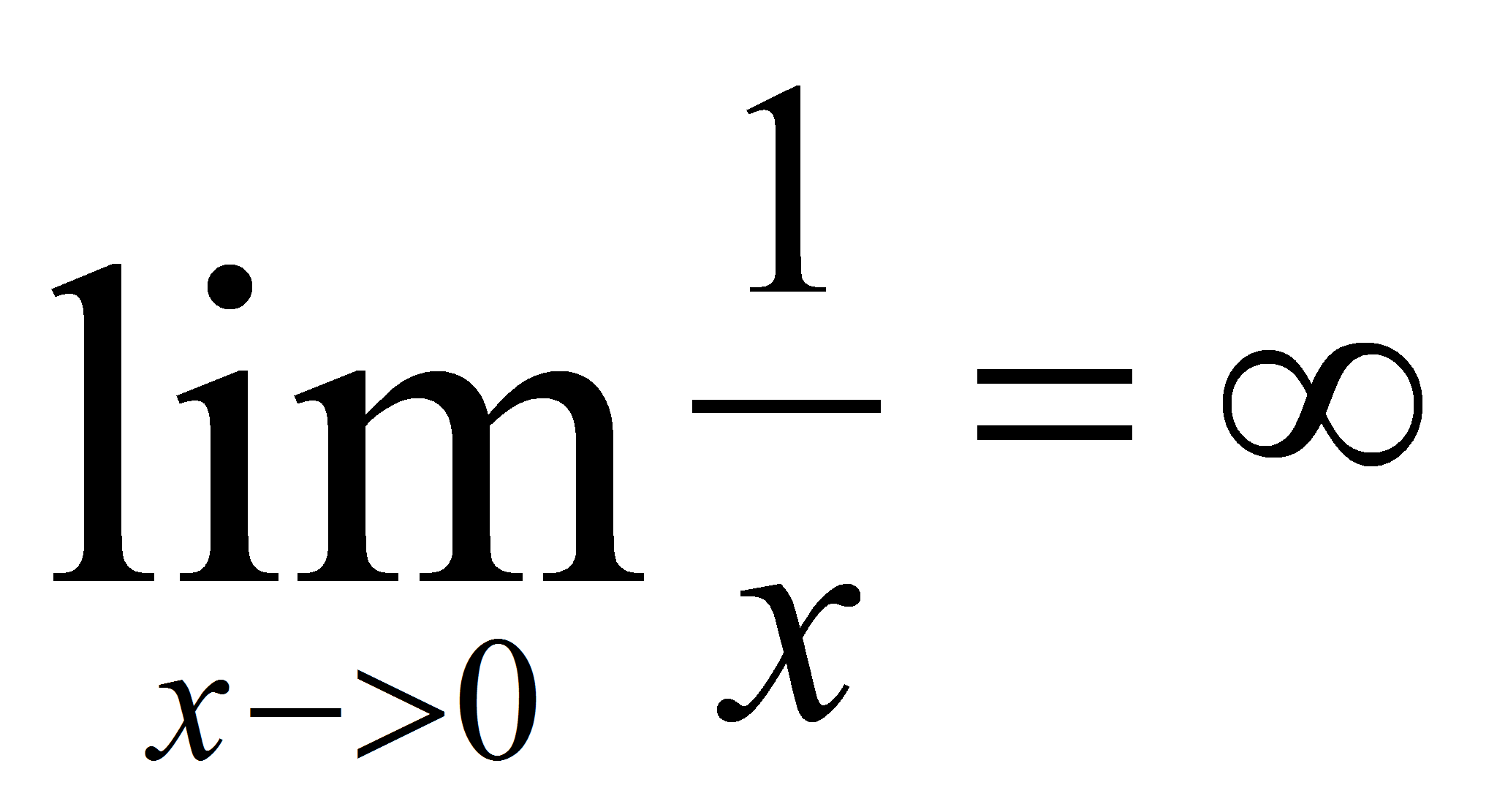 .
. ¡Escucha ahora!
¡Te lo puedo decir más alto pero no más claro! 1/0 no
es igual a infinito, el límite de 1/x cuando x tiende hacia cero es infinito.
1/0 es una indeterminación y el infinito es sólo un concepto
matemático para expresar que una función crece sin mesura.
¡Escucha ahora!
¡Te lo puedo decir más alto pero no más claro! 1/0 no
es igual a infinito, el límite de 1/x cuando x tiende hacia cero es infinito.
1/0 es una indeterminación y el infinito es sólo un concepto
matemático para expresar que una función crece sin mesura.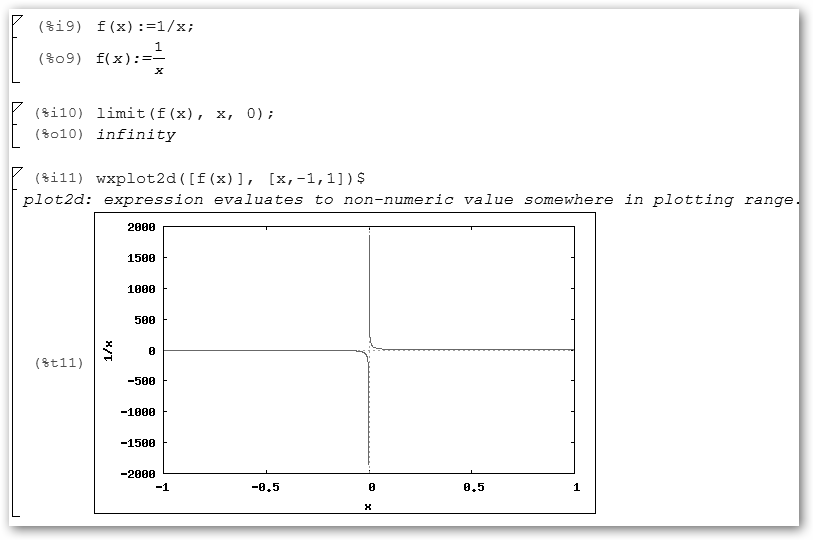


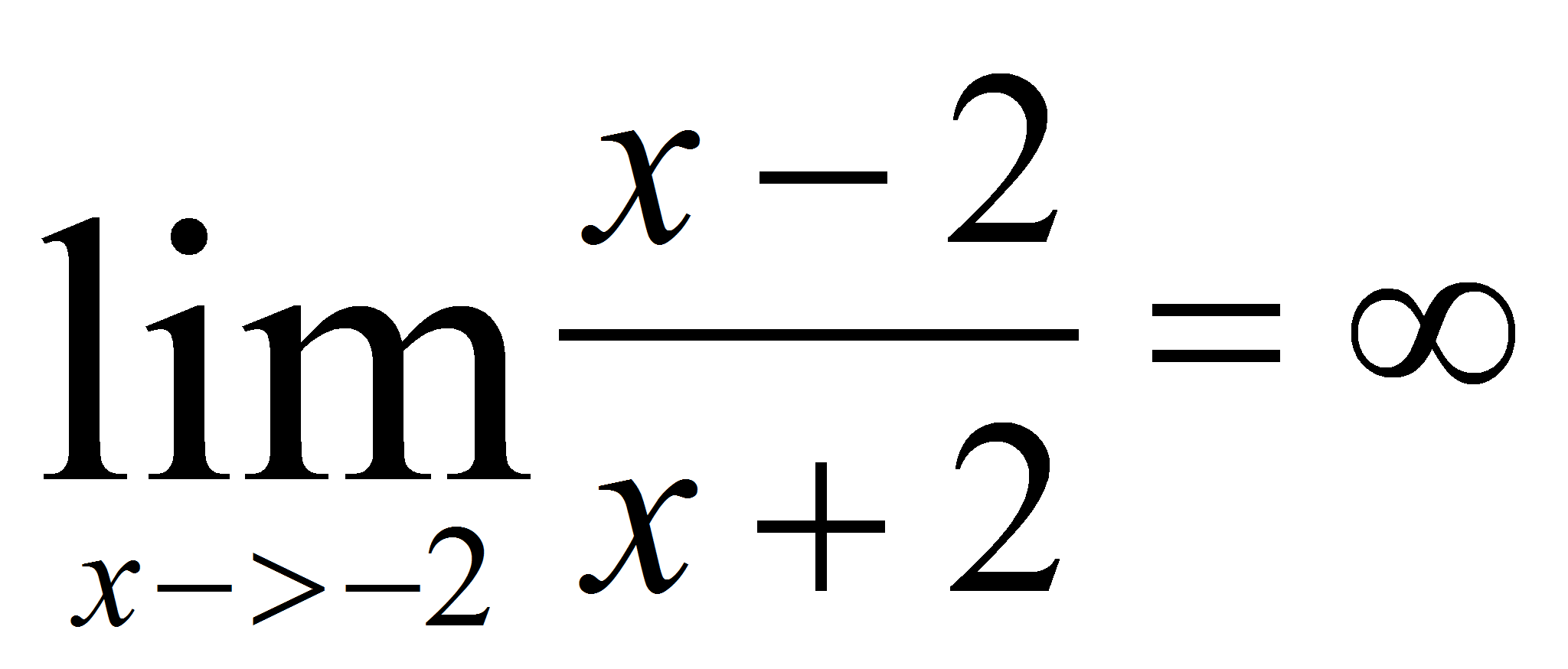 y, por tanto, una asíntota vertical en la recta
x=-2.
y, por tanto, una asíntota vertical en la recta
x=-2. 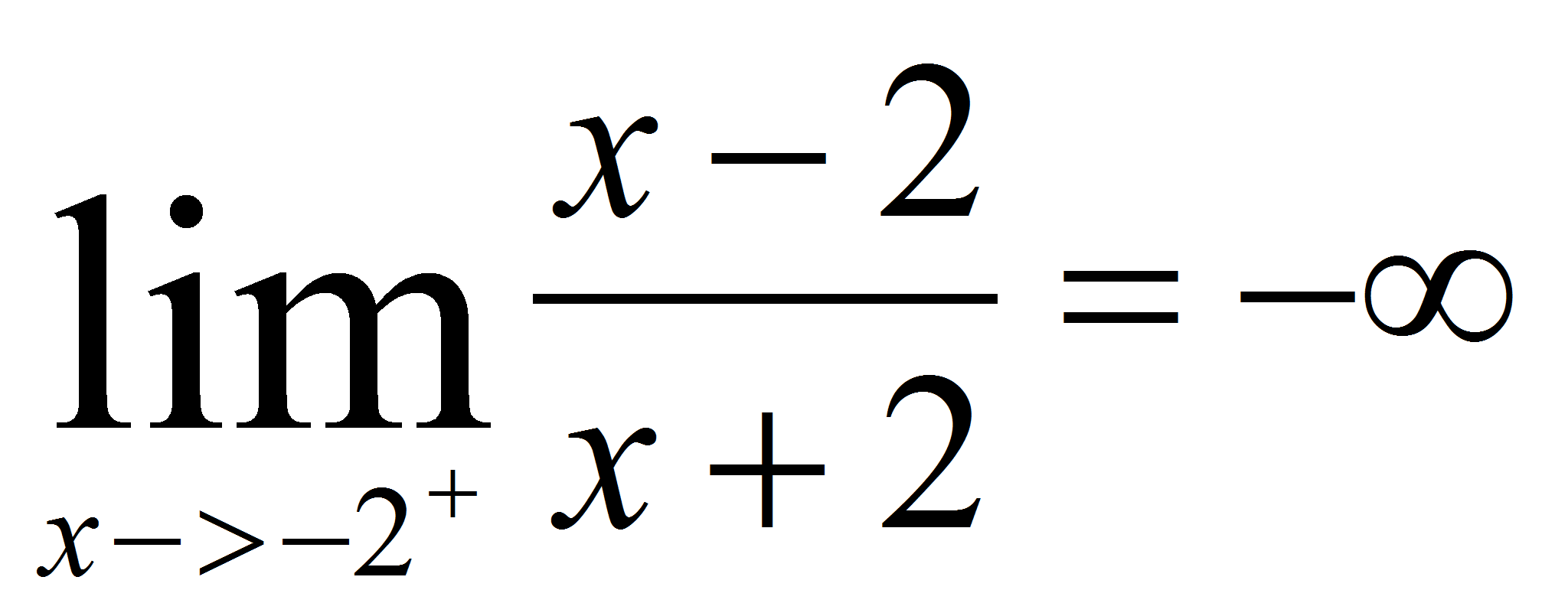 y el límite por la izquierda limit(f(x), x, -2, minus);
obtenemos que
y el límite por la izquierda limit(f(x), x, -2, minus);
obtenemos que 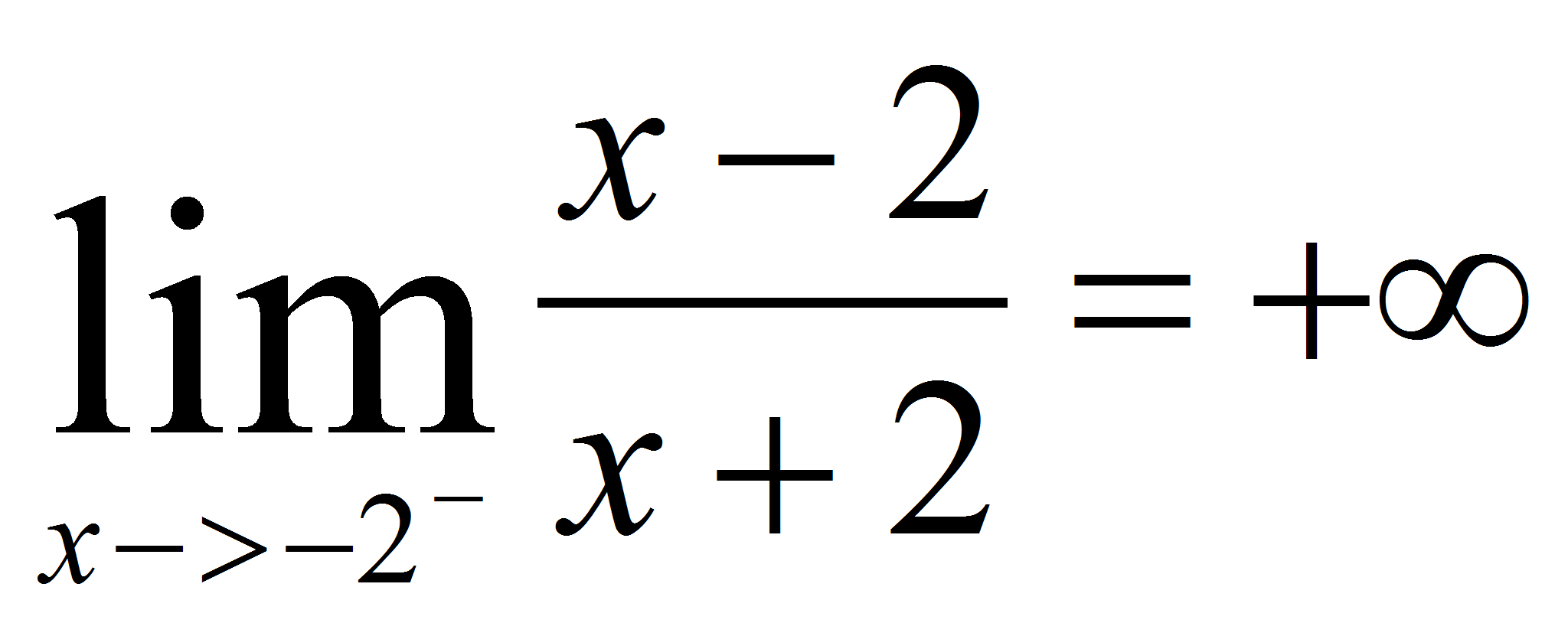 . Además, limit(f(x),
x, infinity); devuelve 1, matemáticamente:
. Además, limit(f(x),
x, infinity); devuelve 1, matemáticamente:
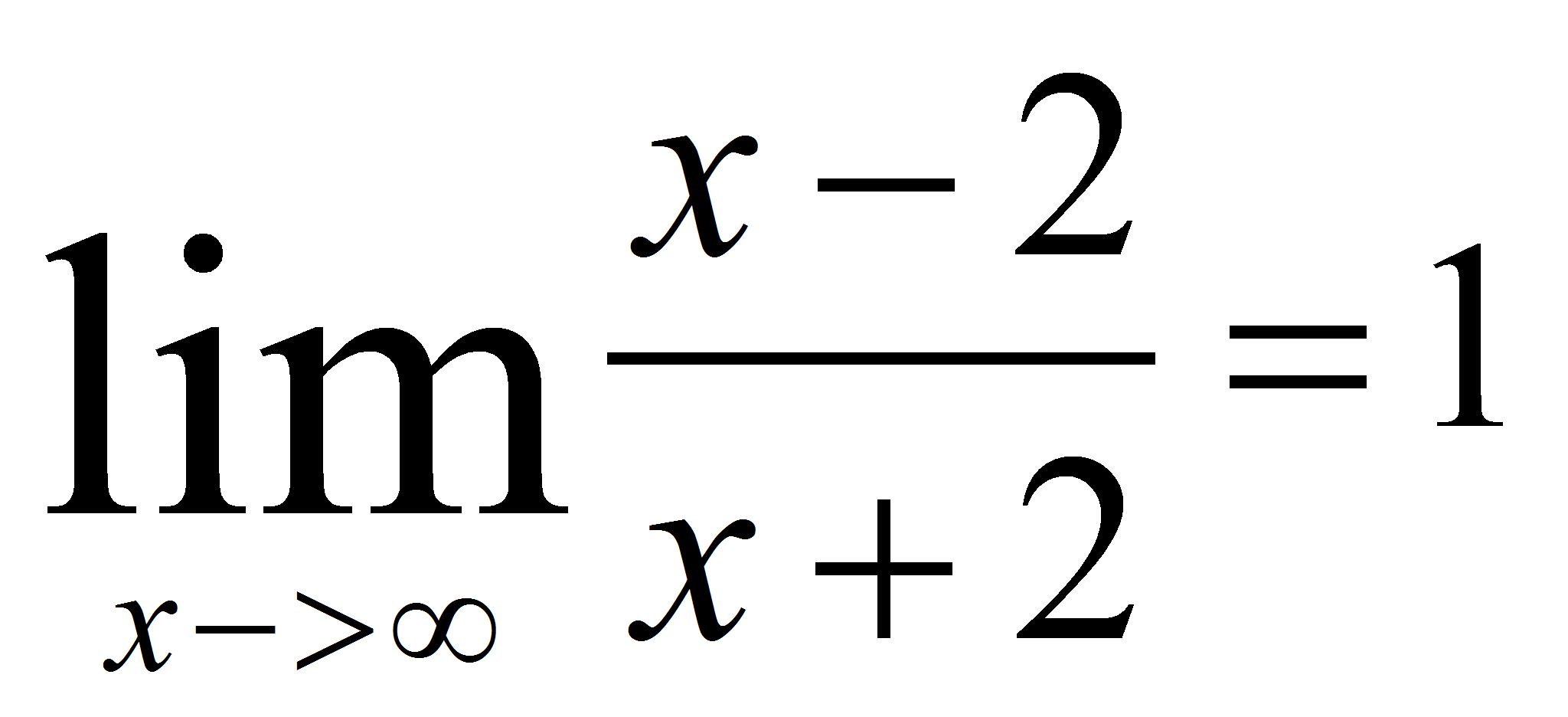 .
.
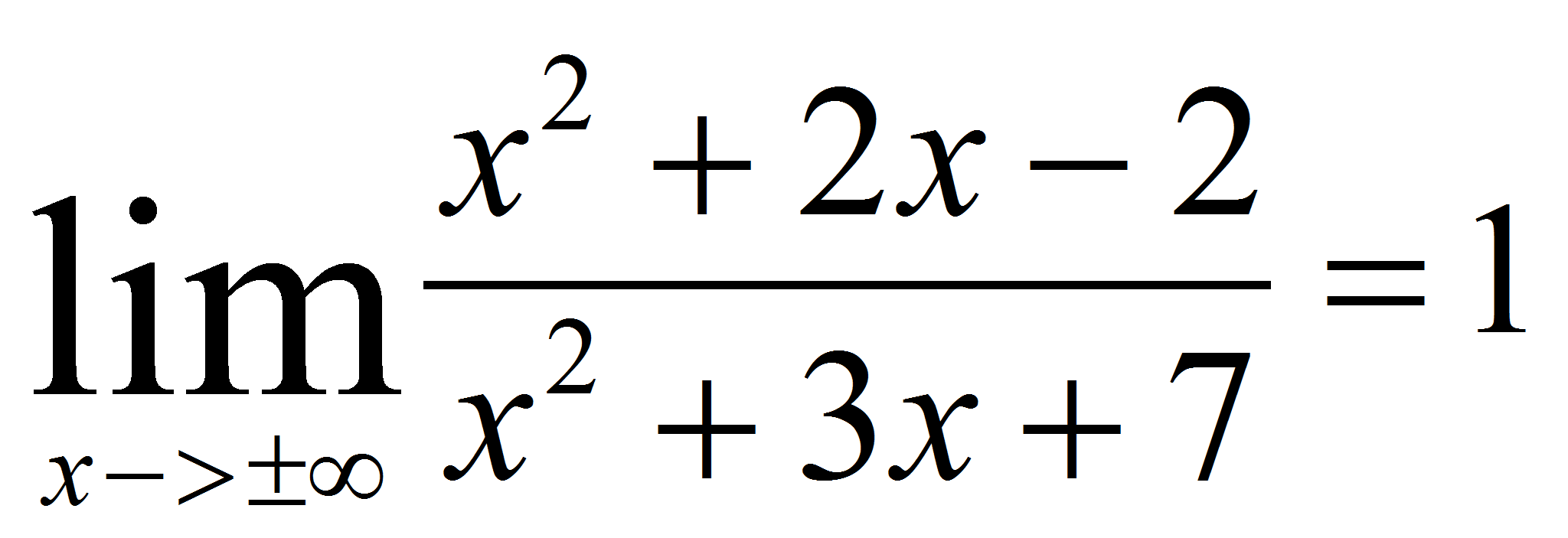 y, por tanto, tiene una asíntota horizontal en y=1.
y, por tanto, tiene una asíntota horizontal en y=1.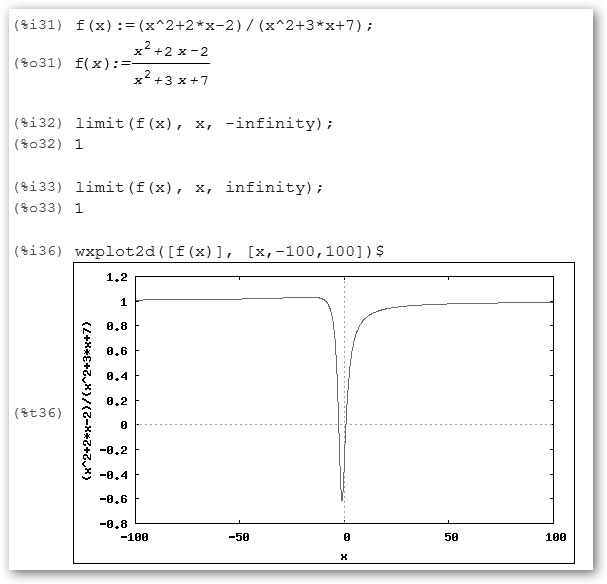
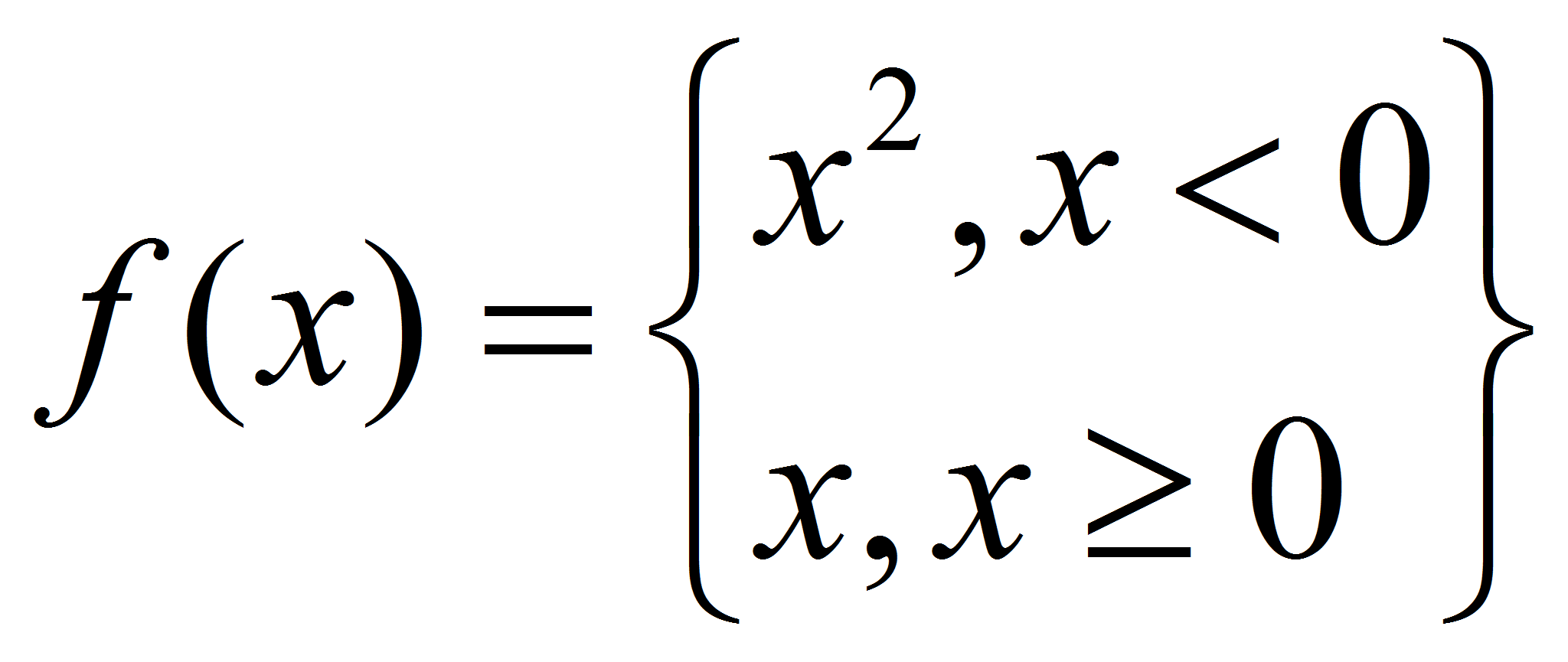 es continua, como se puede apreciar en las figuras porque las
funciones x2
y x lo son. En el punto conflictivo 0, obtenemos lo siguiente:
es continua, como se puede apreciar en las figuras porque las
funciones x2
y x lo son. En el punto conflictivo 0, obtenemos lo siguiente: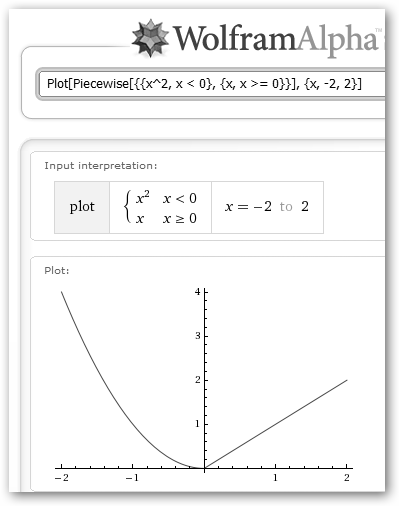

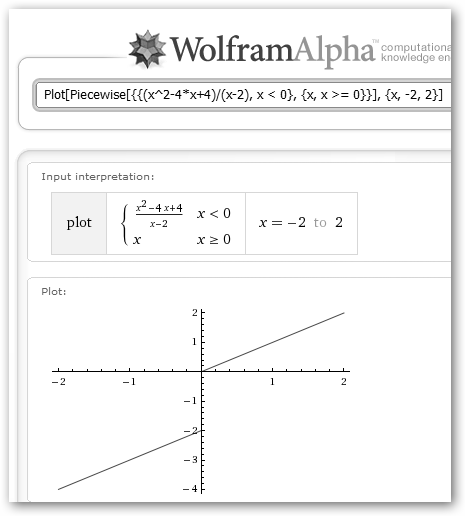
 en el cero!
en el cero! 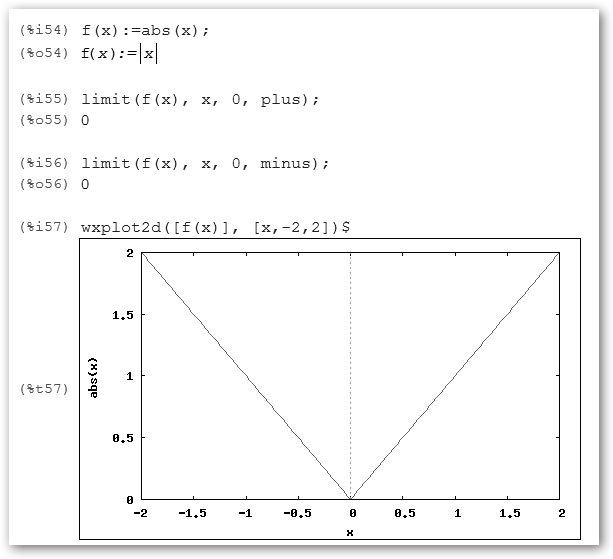
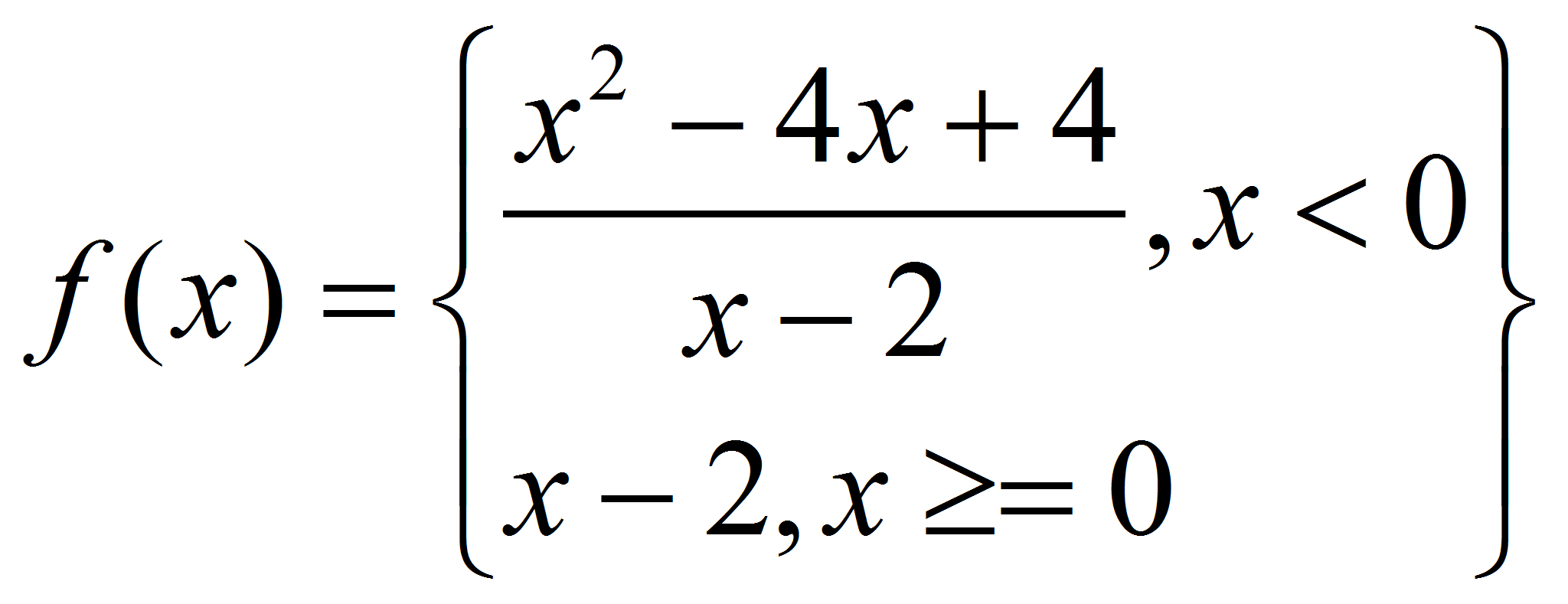


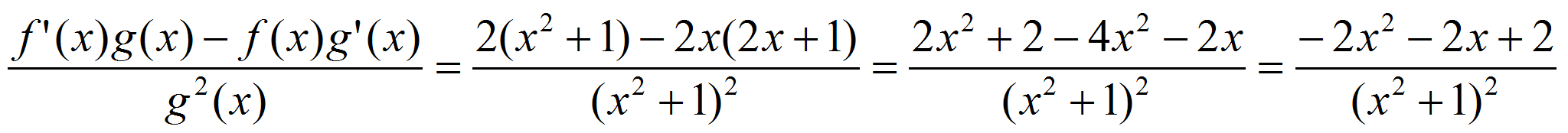

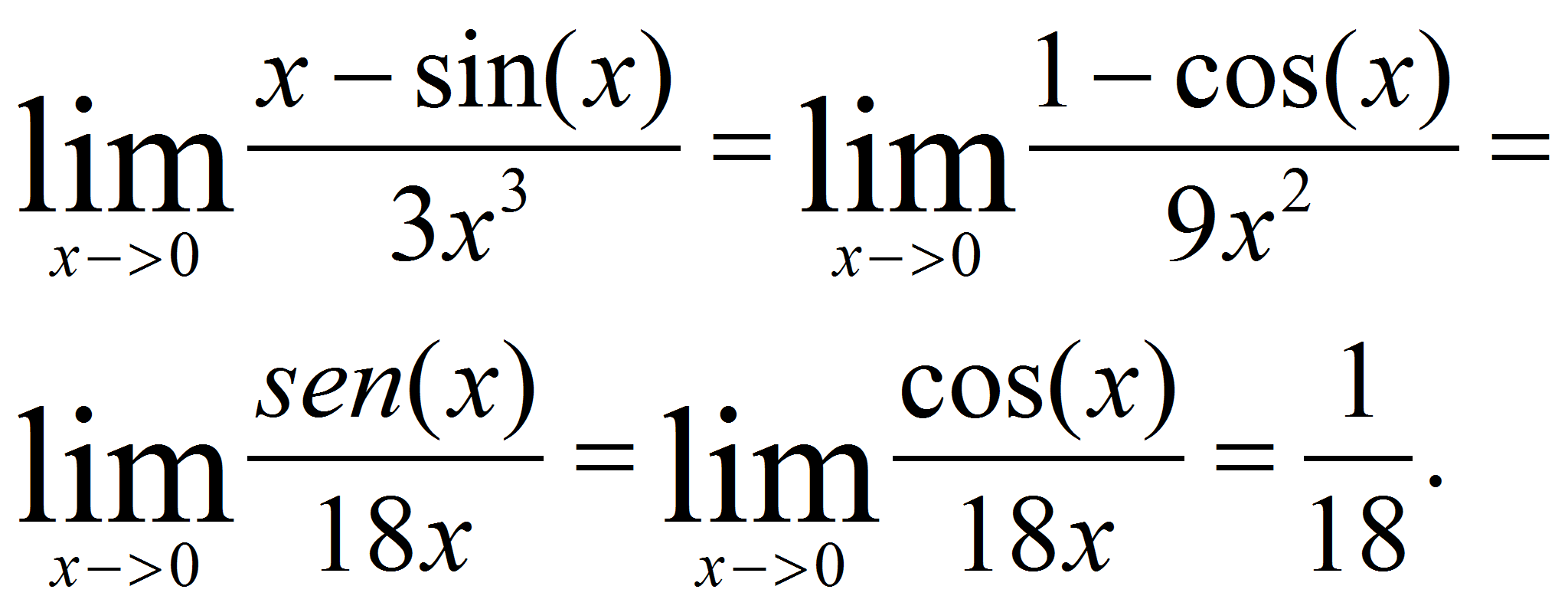
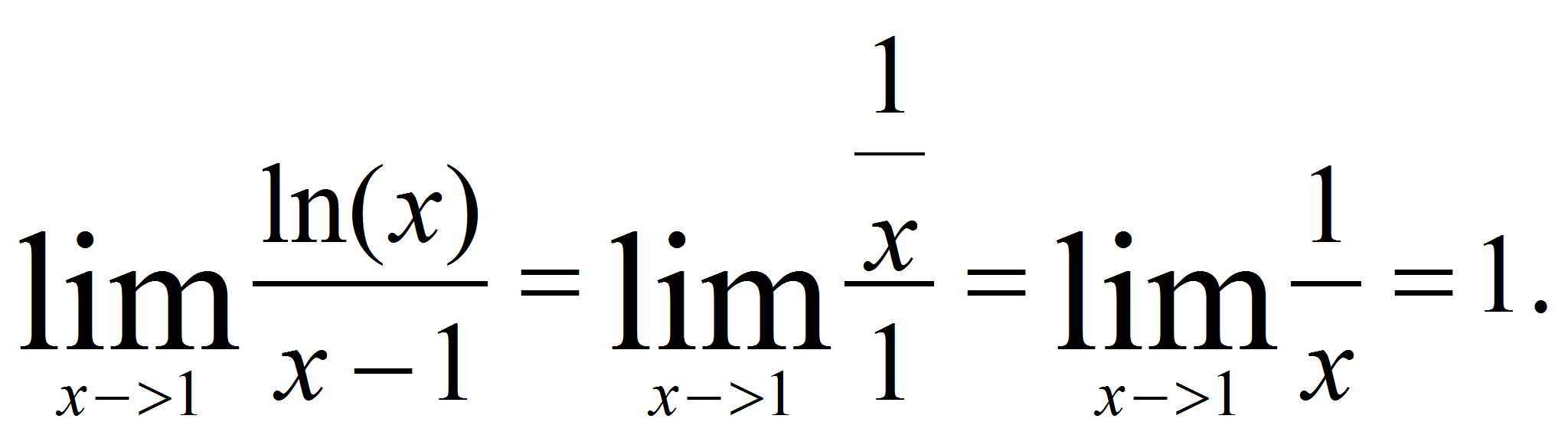
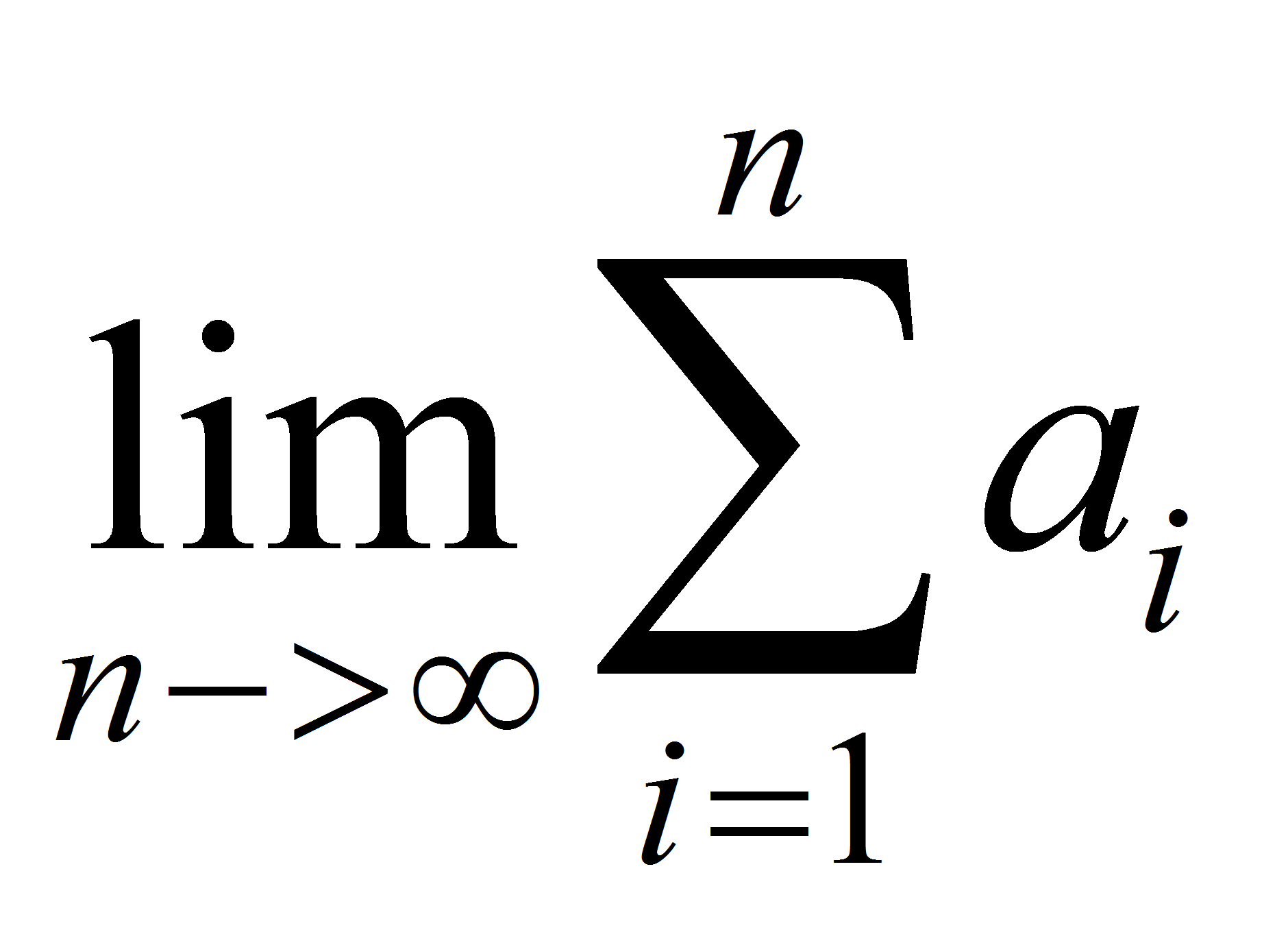 existe, la serie converge, en caso contrario diverge.
existe, la serie converge, en caso contrario diverge.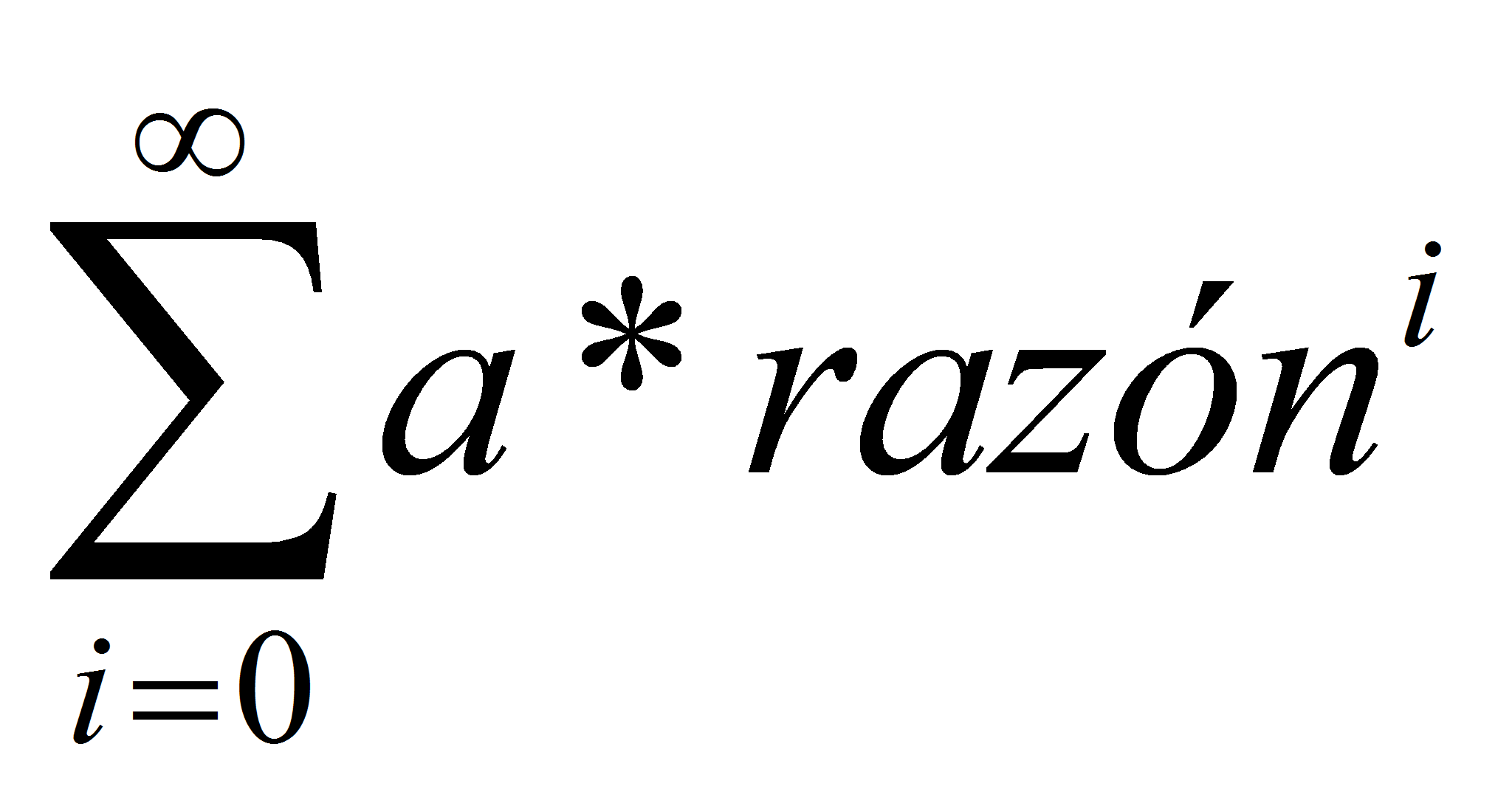 con razón=1/3<1 y término inicial a=1, que por
lo tanto converge a
con razón=1/3<1 y término inicial a=1, que por
lo tanto converge a
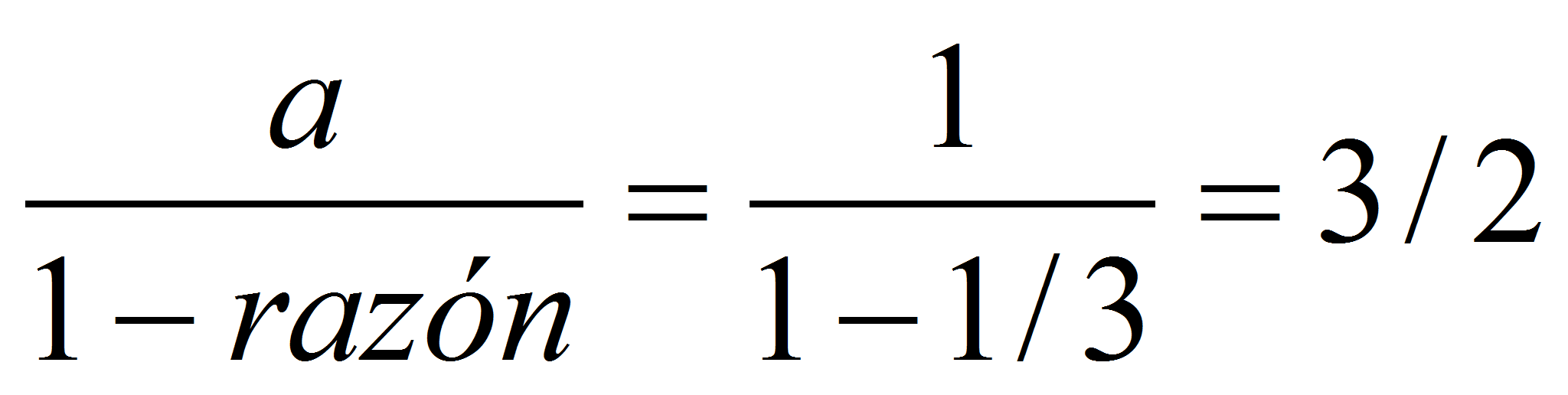 .
.
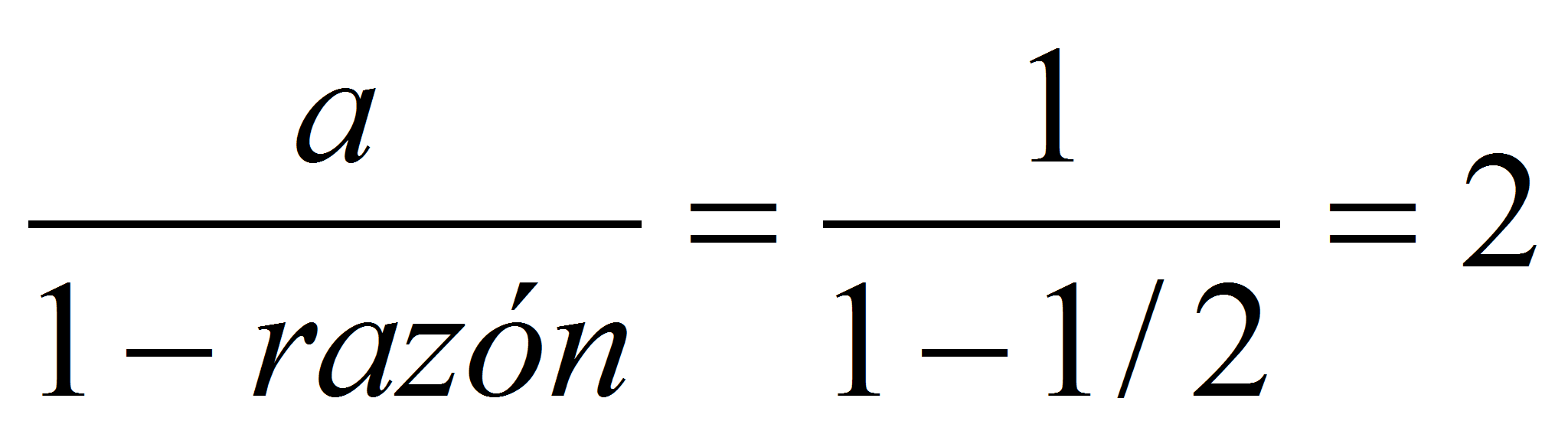 ).
Prueba otro tipo de series: (1) a[n]:=1/(n^2); (2)
sum(a[i], i, 1, inf), simpsum; y obtendrás
).
Prueba otro tipo de series: (1) a[n]:=1/(n^2); (2)
sum(a[i], i, 1, inf), simpsum; y obtendrás
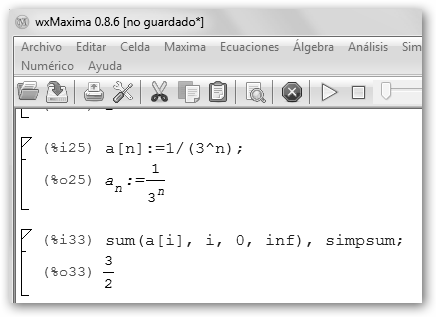


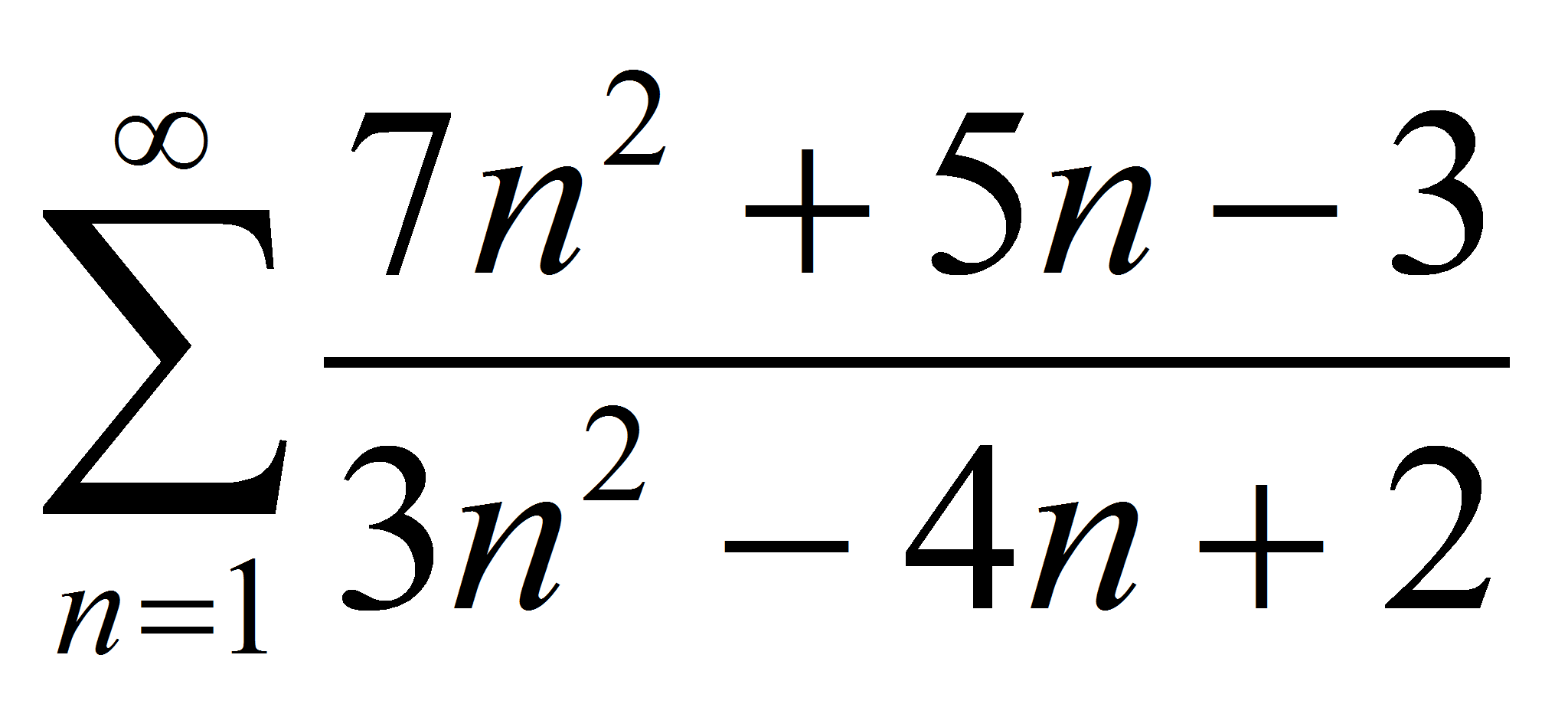 precisamente porque el
precisamente porque el
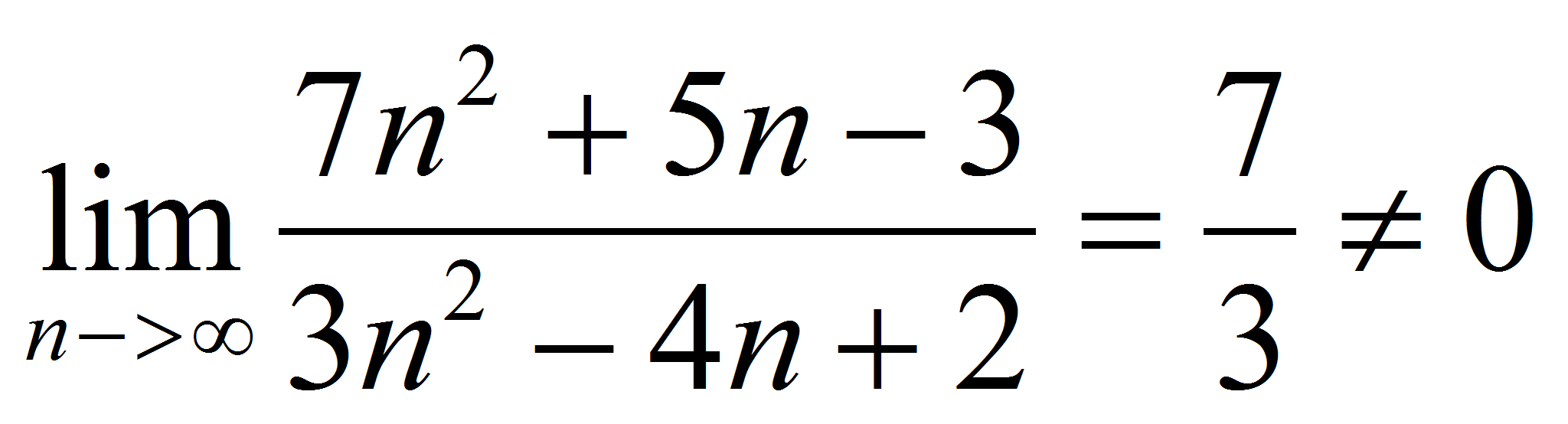 .
.

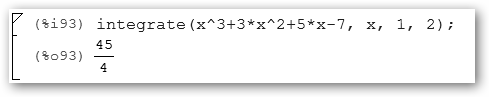
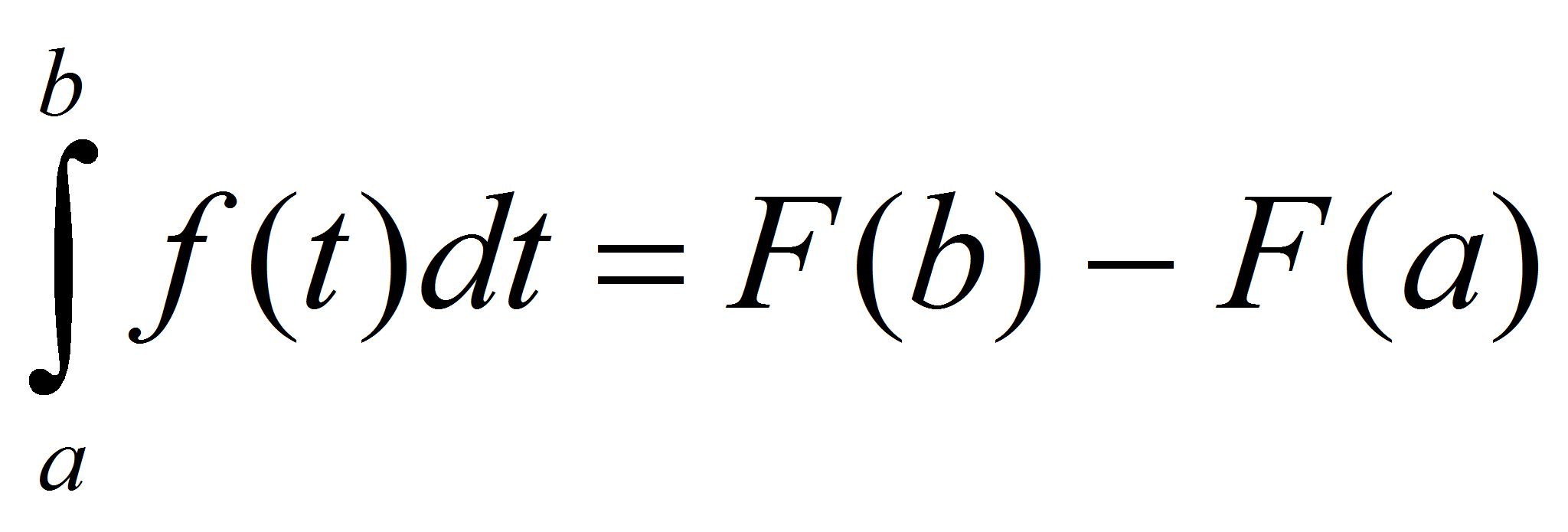 y que la integral de un polinomio
y que la integral de un polinomio
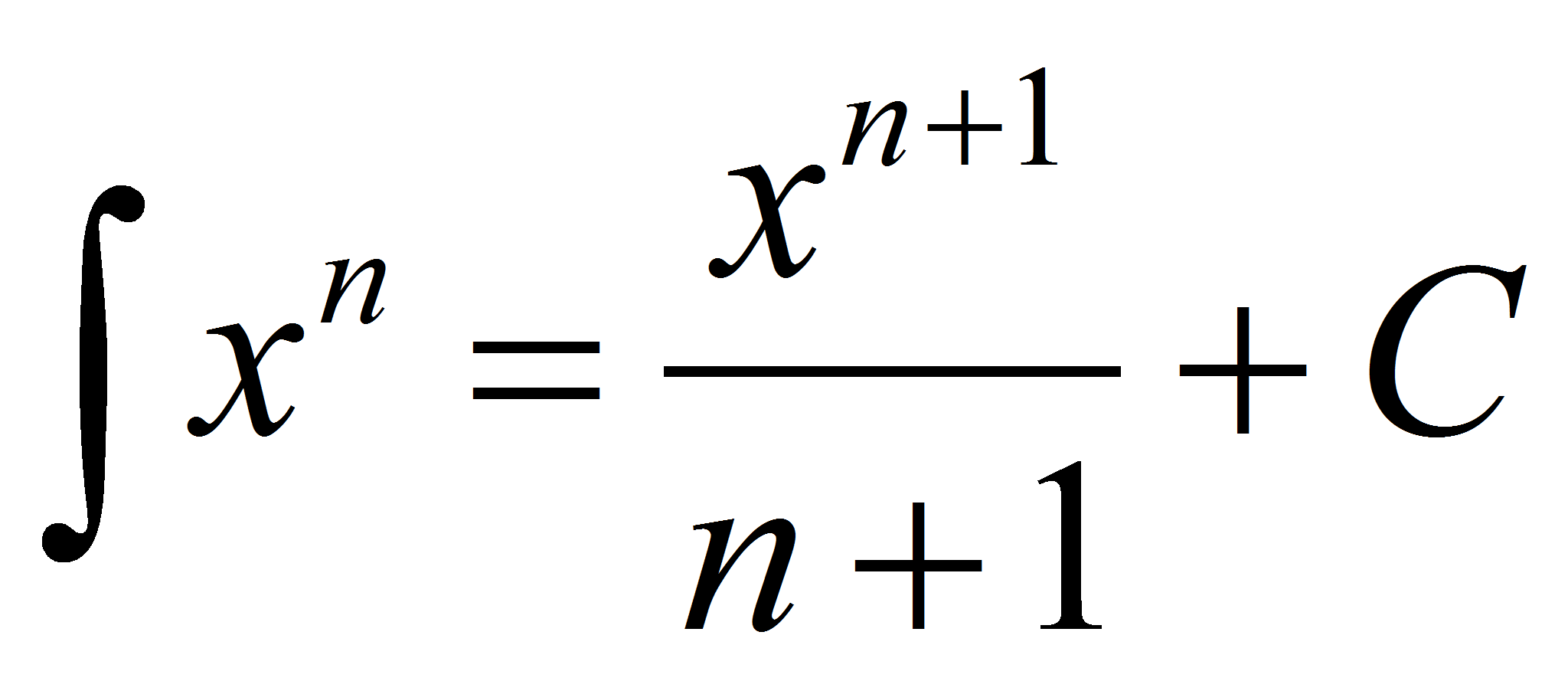 .
.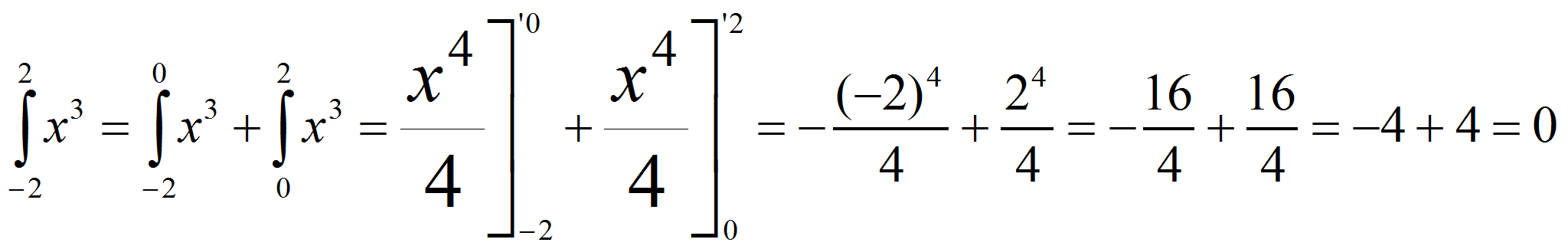
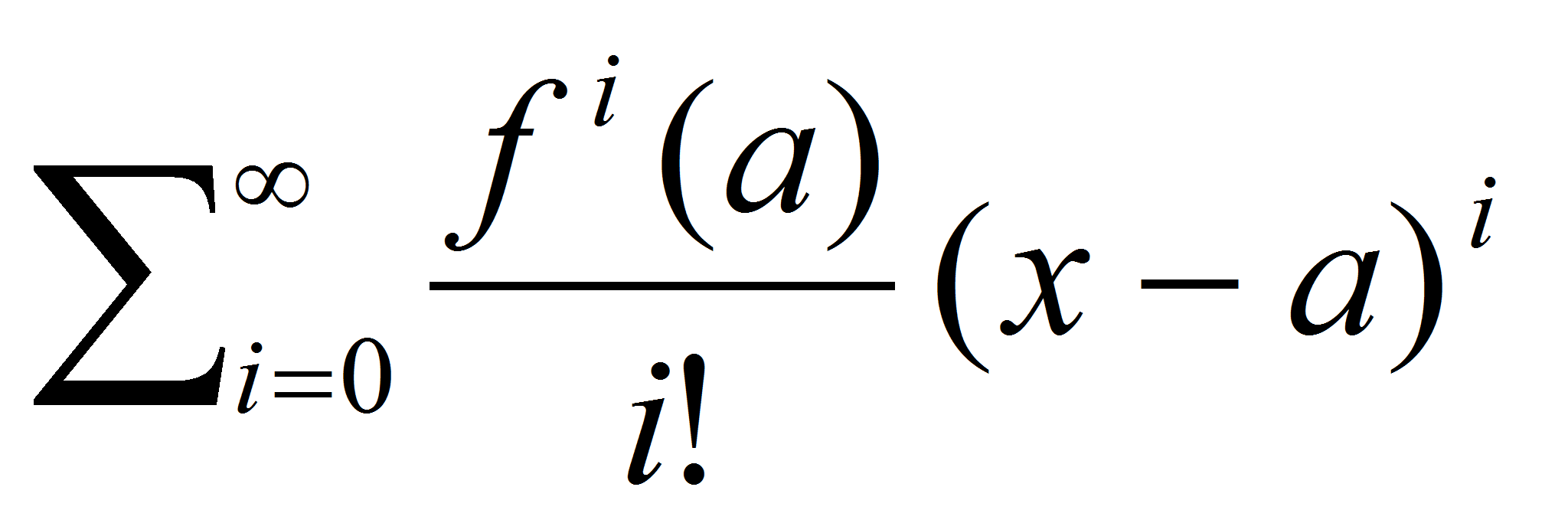 .
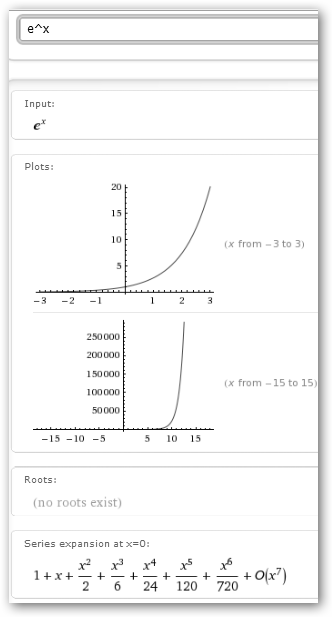
.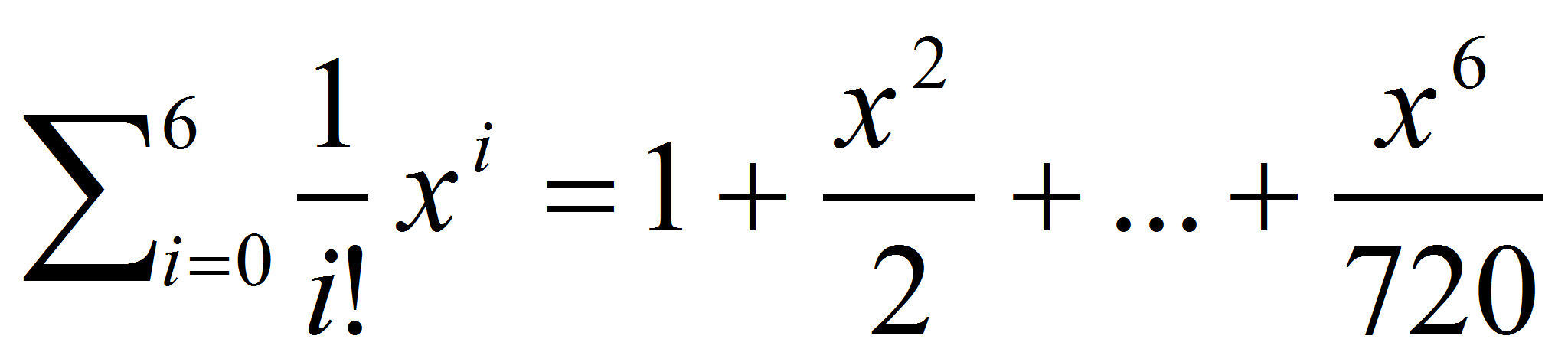 . En WolframAlpha basta con escribir la función, aunque
se puede explícitamente indicarlo: series e^x at x=0 to order 6.
Prueba también series tan(x) at x=0 to order 6
y obtendrás x+x3/3+2x5/15.
. En WolframAlpha basta con escribir la función, aunque
se puede explícitamente indicarlo: series e^x at x=0 to order 6.
Prueba también series tan(x) at x=0 to order 6
y obtendrás x+x3/3+2x5/15. 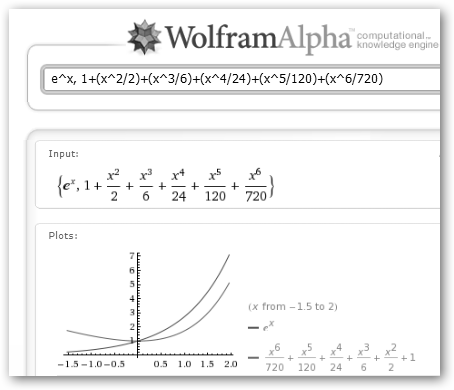
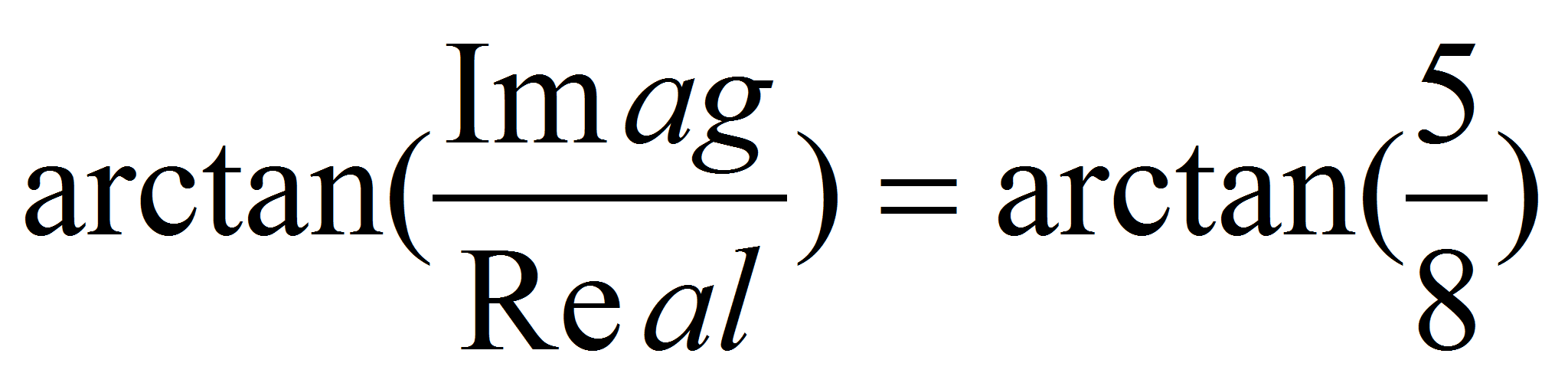 ≈0.5586.
≈0.5586.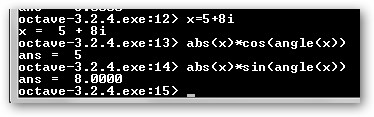
 Todo
tiene solución menos la muerte.
Todo
tiene solución menos la muerte.

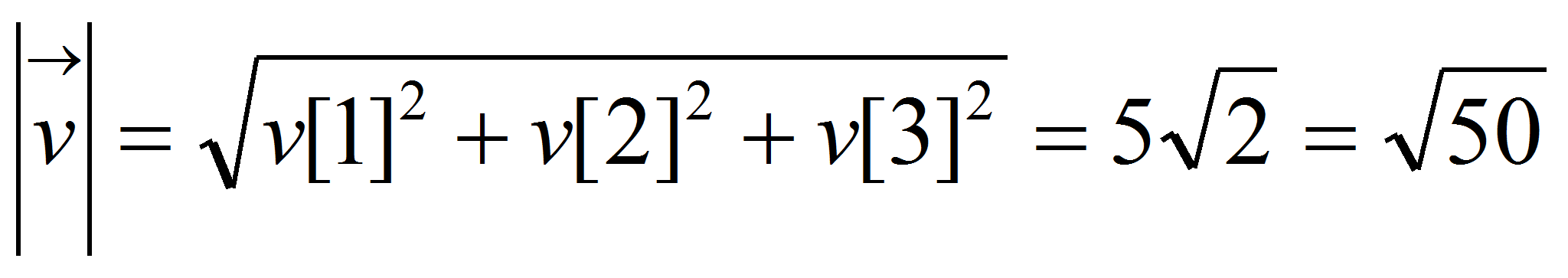

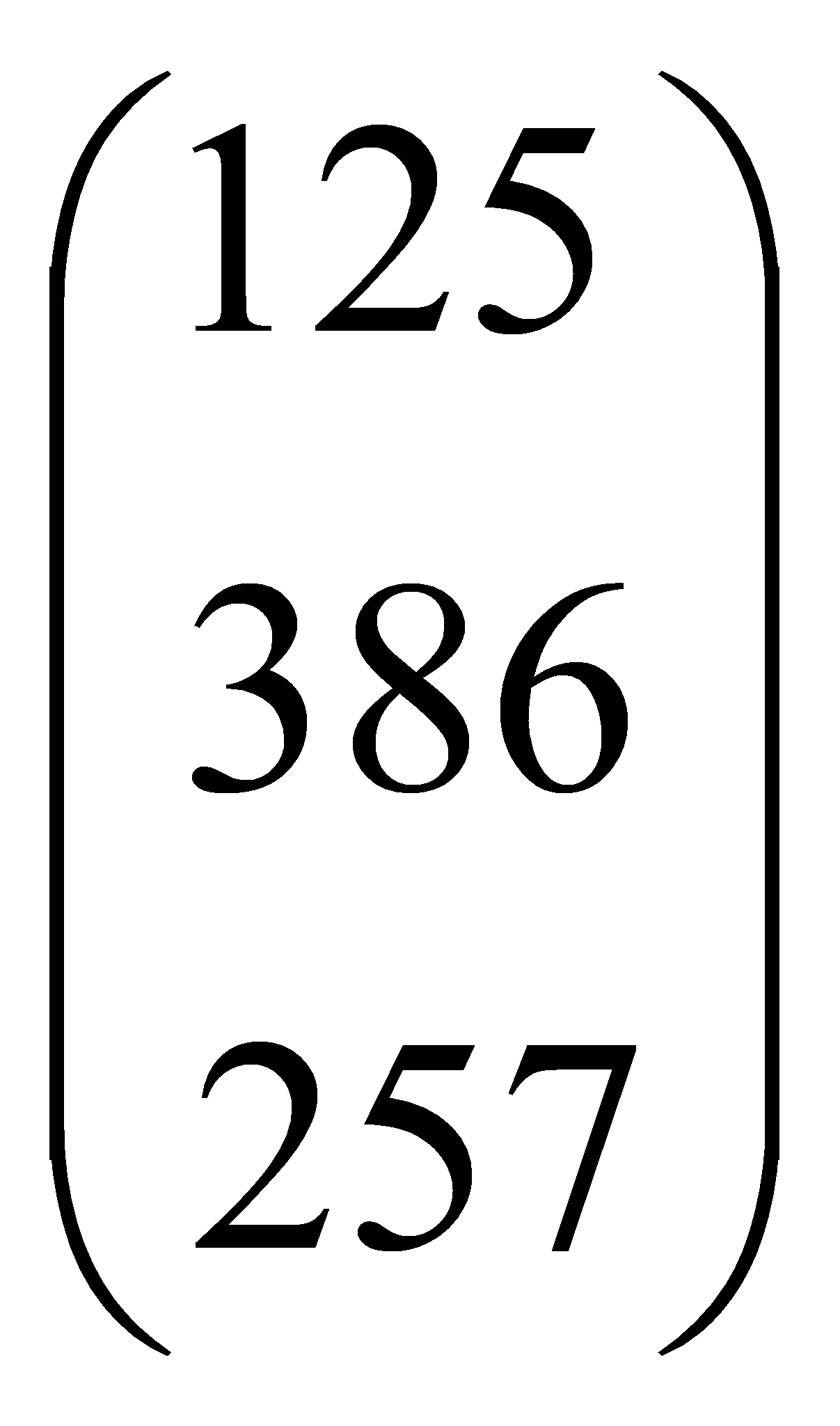 ,
una matriz cuadrada con tres filas y tres columnas.
,
una matriz cuadrada con tres filas y tres columnas.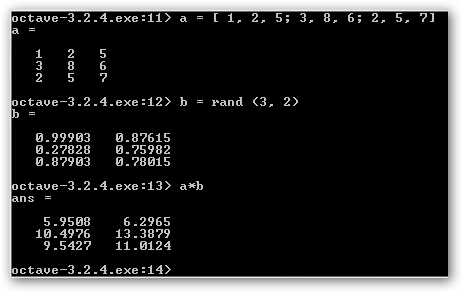


 pero con distintos collares”.
pero con distintos collares”.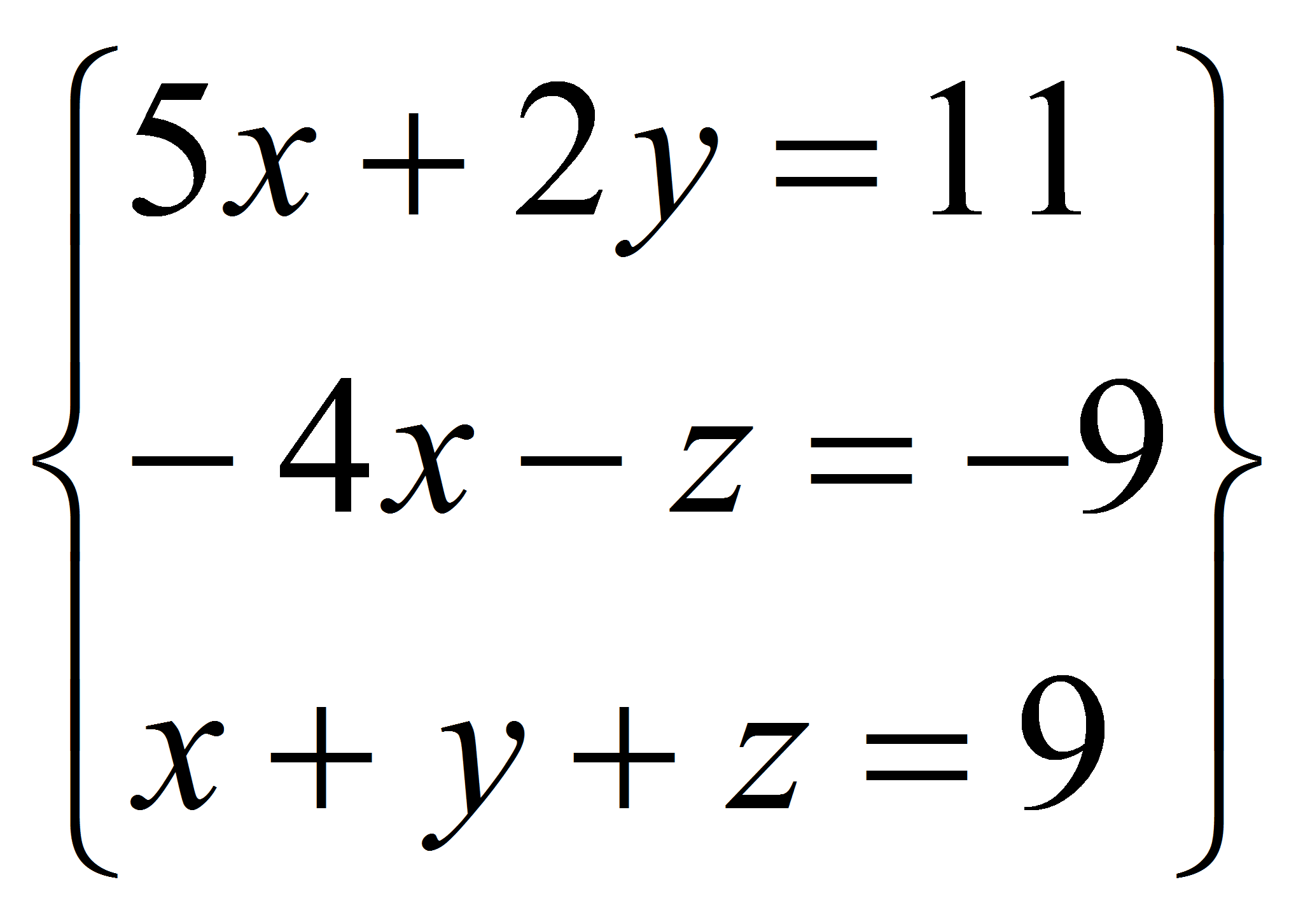


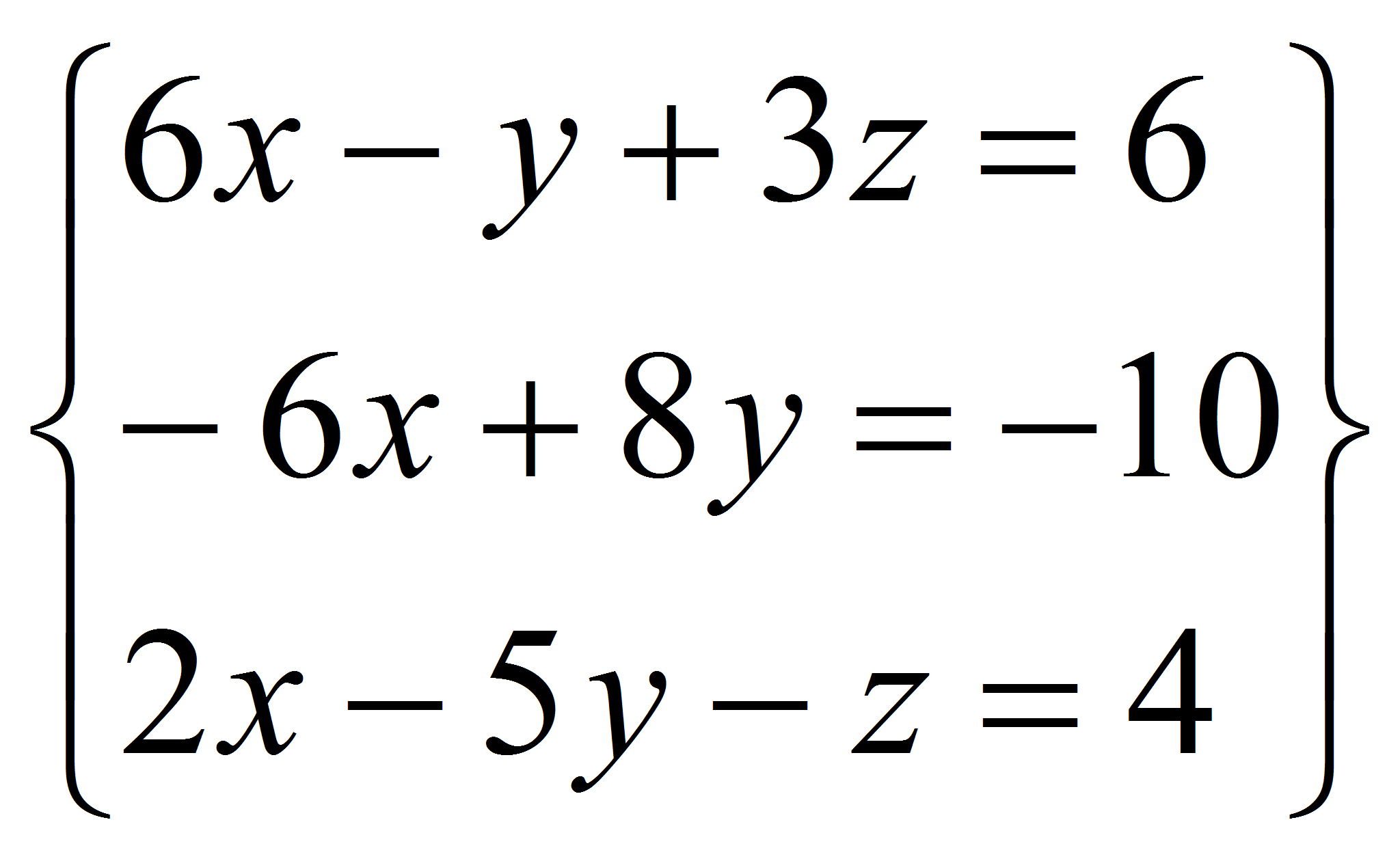

 y calidad puedes utilizar LaTeX con alguno de sus muchos editores:
y calidad puedes utilizar LaTeX con alguno de sus muchos editores: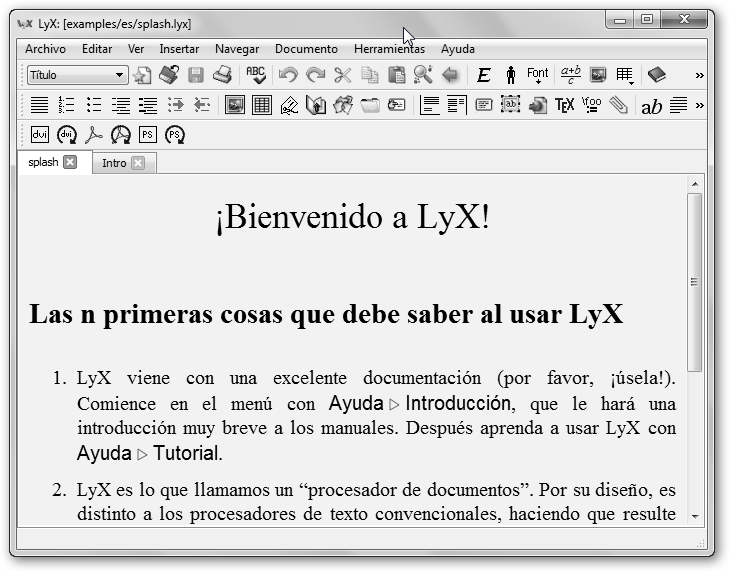
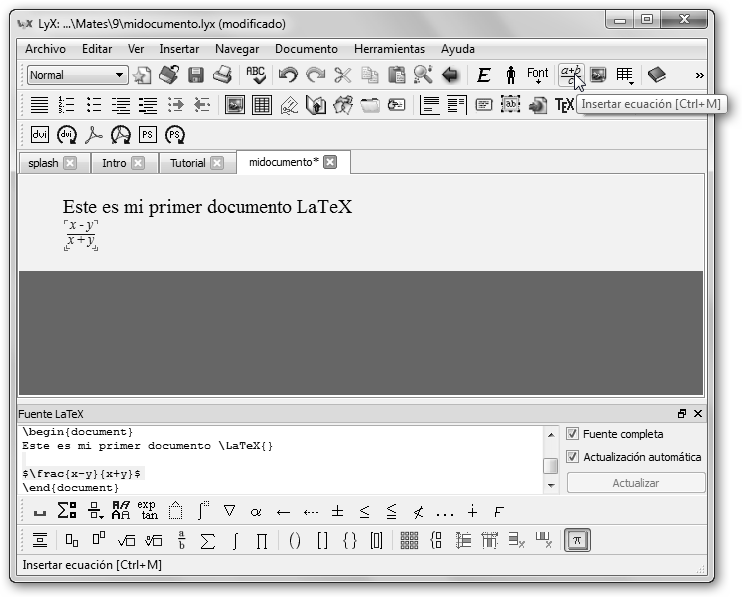
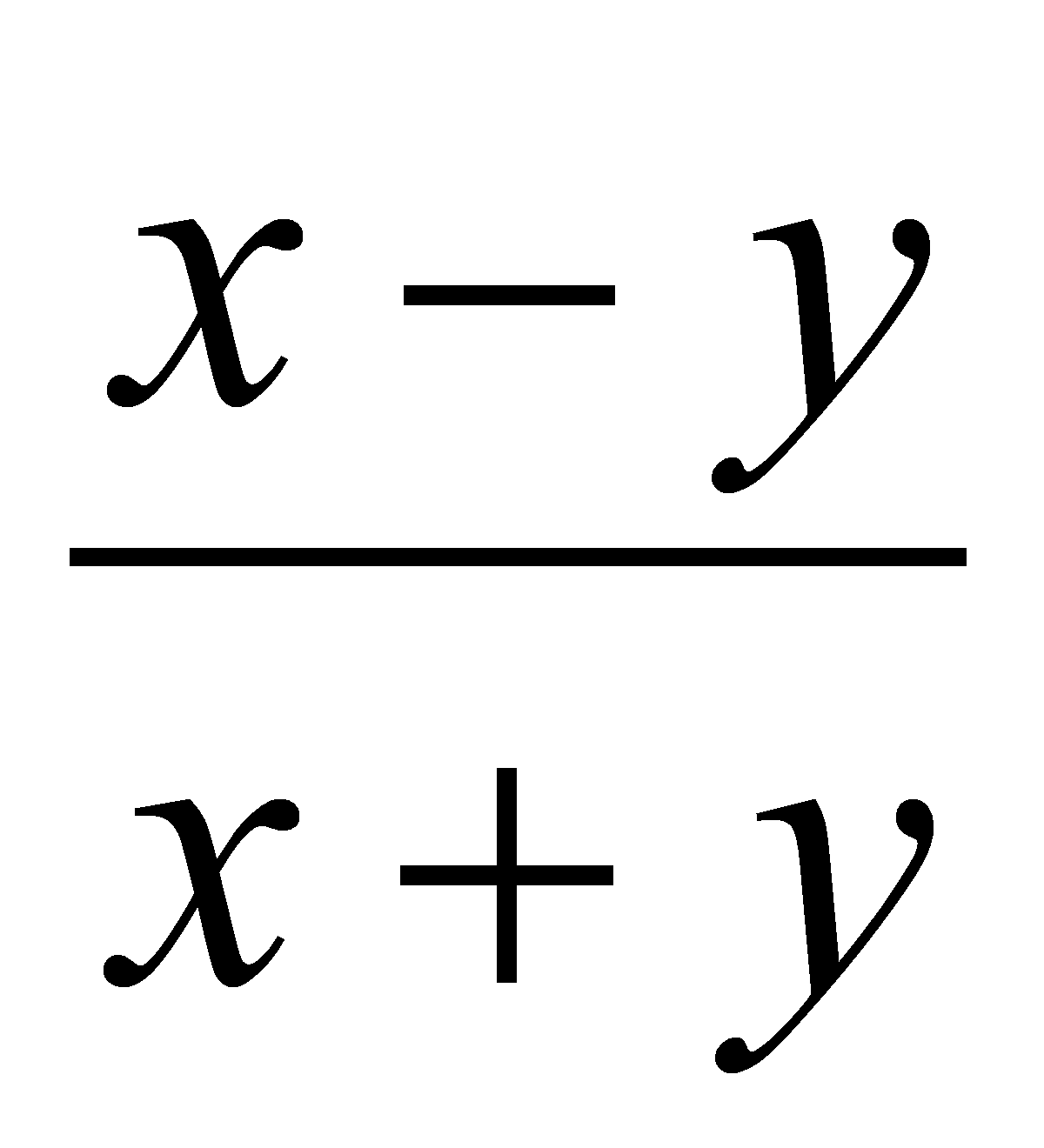 equivale a $\frac{x-y}{x+y}$ o que
$\sqrt[3]{8}=2$ es el código de
equivale a $\frac{x-y}{x+y}$ o que
$\sqrt[3]{8}=2$ es el código de