6. Teoría de Conjuntos y Álgebra
6.1. Introducción a la teoría de conjuntos.
6.2. Peleándonos con polinomios.
6.2.1. Operaciones con polinomios.
6.2.3. Factorización de polinomios
6.2.4. Raíces de un polinomio.
6.3. Ecuaciones de primer grado.
6.4. Ecuaciones de segundo grado.
6.5. Sistemas de dos ecuaciones con dos incógnitas.
6.1. Introducción a la teoría de conjuntos.
|
Con Maxima podemos trabajar con conjuntos. Pero,… ¿qué es un conjunto?
Pues podemos decir que es una colección de cosas, de
objetos, por ejemplo, animales, vocales, palabrotas (¡sí!,
lo has adivinado. ¡No voy a poner ejemplos!, que tiene más
peligro que una |
Básicamente
se trata de una lista, un saco o una agrupación de
elementos no ordenados (el orden es irrelevante, {1, 2} es
el mismo conjunto que {2, 1}) y que no se repiten |
En Maxima (arráncalo desde Inicio, Todos los programas, Máxima-5.22.1, wxMaxima) podemos trabajar con conjuntos muy fácilmente. Veamos cómo:
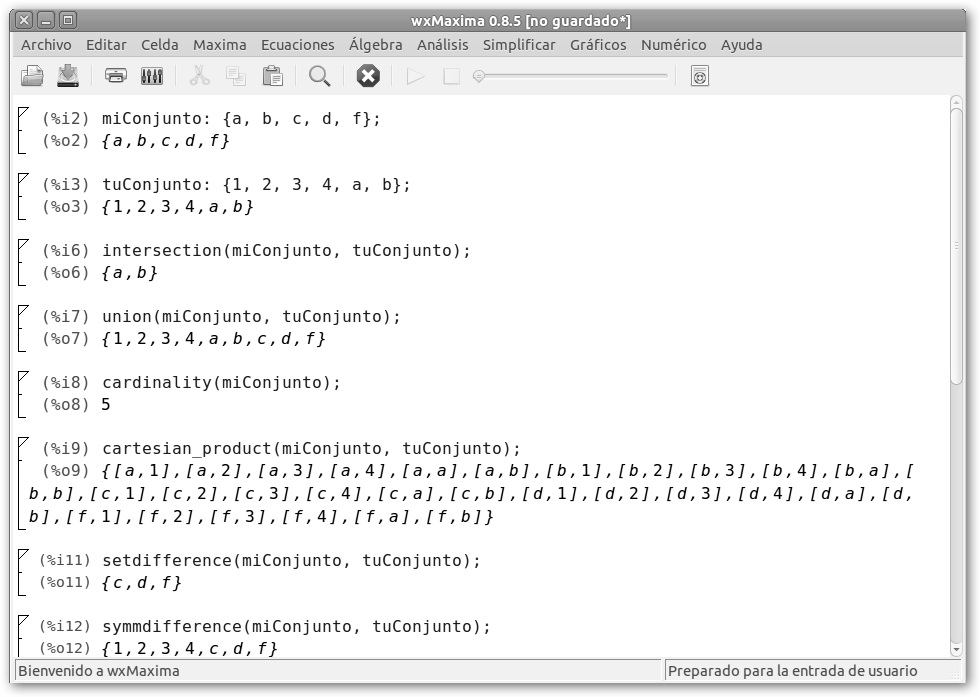
* Definir los conjuntos: enumerar los elementos de los que están formados, miConjunto : {a, b, c, d, f}; (¡no olvides el punto y coma “;” del final, para eso estos programas son muy sibaritas! Y presiona simultáneamente Ctrl + INTRO), es decir, los elementos están agrupados entre llaves y separados por comas. El número de elementos de los que se compone un conjunto es la cardinalidad. La cardinalidad de miConjunto es cinco y se solicita con: cardinality(miConjunto);. Esta es la definición por extensión, es decir, escribiendo todos los elementos que pertenecen al conjunto. Maxima también permite la definición por comprensión, es decir, indicando la característica común de todos los elementos. Un ejemplo sería otroConjunto : divisors(32); sería el conjunto de los divisores de 32, {1, 2, 4, 8, 16, 32}.
* Veamos otra forma más compleja de definir funciones: setify(makelist(fib(n), n, 1, 10)); devuelve un conjunto formado a partir de la lista (setify realiza la conversión de listas a conjuntos) de los primeros números de la serie de Fibonacci (fib(n) devuelve el n-esimo número de la serie de fibonacci, donde fib(0)=0, fib(1)=1, fib(2)=1, fib(3)=2,…) {1, 2, 3, 5, 8, 13, 21, 34, 55}. Sin embargo, la cardinalidad de {1, 2, 3, 5, 8, 13, 21, 34, 55} es 9 y nosotros hemos pedido los 10 primeros elementos de la serie, ¿sabes por qué? Pues porque makelist(fib(n), n, 1, 10) efectivamente devuelve 10 números [1, 1, 2, 3, 5, 8, 13, 21, 34, 55], pero uno de los “1”, lo elimina setify para formar un conjunto.
* Observa, por tanto, que todos los elementos del conjunto son distintos. Así podemos definir conjuntos como C = setify ([1, 2, 3, a, b, c]); y el resultado será el mismo que si escribiéramos C=setify ([1, 2, 3, a, b, c, 1]); es decir, C = {1, 2, 3, a, b, c}.
* Además en un conjunto el orden de sus elementos es irrelevante, así setequalp ({a, b, c, d, e, f}, {f, e, d, c, b, a}); (setequalp responde si los dos conjuntos pasados como argumentos son iguales), devuelve true, verdadero. En cambio, setequalp ({a, b, c, d, e, f}, {f, e, d, c, b, a, h}); devuelve false, falso.
* Realizar la
intersección de dos conjuntos miConjunto ∩
tuConjunto: intersection(miConjunto, tuConjunto); devuelve
los elementos que están tanto en miConjunto como en
tuConjunto, en el ejemplo, a y b (define previamente tuConjunto:
{1, 2, 3, 4, a, b};). Formalmente:
![]() {elemento
: elemento
{elemento
: elemento
![]() miConjunto
y elemento
miConjunto
y elemento![]() tuConjunto}.
Si la intersección de dos conjuntos es vacía se dice
que son disjuntos. En Maxima la orden a utilizar es
disjointp, por ejemplo, disjointp(miConjunto, tuConjunto);
devuelve false porque ambos conjuntos no son disjuntos, en realidad,
comparten a y b. Sin embargo, disjointp({2, 4, 6, 8}, {1, 3, 5,
7}); es true.
tuConjunto}.
Si la intersección de dos conjuntos es vacía se dice
que son disjuntos. En Maxima la orden a utilizar es
disjointp, por ejemplo, disjointp(miConjunto, tuConjunto);
devuelve false porque ambos conjuntos no son disjuntos, en realidad,
comparten a y b. Sin embargo, disjointp({2, 4, 6, 8}, {1, 3, 5,
7}); es true.
* Solicitar la unión
de dos conjuntos miConjunto
![]() tuConjunto:
union(miConjunto, tuConjunto); devuelve los elementos que
están en los dos conjuntos, es decir, en miConjunto,
tuConjunto o en ambos {1, 2, 3, 4, a, b, c, d, f}.
Matemáticamente:
tuConjunto:
union(miConjunto, tuConjunto); devuelve los elementos que
están en los dos conjuntos, es decir, en miConjunto,
tuConjunto o en ambos {1, 2, 3, 4, a, b, c, d, f}.
Matemáticamente:![]() {elemento
: elemento
{elemento
: elemento
![]() miConjunto
o elemento
miConjunto
o elemento![]() tuConjunto}.
tuConjunto}.
* Otra operación
que solicitamos es el producto cartesiano miConjunto X
tuConjunto: cartesian_product(miConjunto, tuConjunto);
conjunto de pares de elementos formados por el primero de miConjunto
y el segundo de tuConjunto: {[a, 1], [a, 2], ...[b, 1], [b, 2],…}.
En lenguaje matemático: miConjunto x tuConjunto =
{(elemento1, elemento2) : elemento1
![]() miConjunto
y elemento2
miConjunto
y elemento2![]() tuConjunto}.
tuConjunto}.
* Pedimos también
(“contra el vicio de pedir, la virtud es no dar”) la
diferencia de dos conjuntos miConjunto\tuConjunto:
setdifference(miConjunto, tuConjunto); es el conjunto de
elementos que están en miConjunto pero que no están en
tuConjunto (observa que a y b si lo estaban) {c, d, f}. Formalmente:
miConjunto\tuConjunto = {elemento : elemento
![]() miConjunto
y elemento
miConjunto
y elemento![]() tuConjunto}.
tuConjunto}.
* Finalmente,
requerimos la diferencia simétrica miConjunto Δ
tuConjunto: symmdifference(miConjunto, tuConjunto); es el
conjunto de elementos que están en miConjunto (a, b, c, d,
f), en tu Conjunto (1, 2, 3, 4, a, b) pero no están en los
dos (eliminamos a y b). Estrictamente hablando: miConjunto Δ
tuConjunto = {elemento : (elemento
![]() miConjunto
˄ elemento
miConjunto
˄ elemento
![]() tuConjunto)
˅ (elemento
tuConjunto)
˅ (elemento
![]() tuConjunto
˄ elemento
tuConjunto
˄ elemento
![]() miConjunto)
}.
miConjunto)
}.
Utilizando
WolframAlpha (www.wolframalpha.com) podemos también
trabajar con conjuntos. En la primera fila solicitamos la
intersección, la unión, la diferencia simétrica
y una operación más compleja: (A![]() B)
∩ C. Nos devuelve una representación gráfica
denominada diagrama de Venn donde la parte más oscura
representa el resultado.
B)
∩ C. Nos devuelve una representación gráfica
denominada diagrama de Venn donde la parte más oscura
representa el resultado.
En la segunda fila solicitamos la intersección, la diferencia y la unión de los conjuntos {a, b, c, d, e} y {a, c, j}.

Aunque a veces los escritores
nos enrollamos más que las persianas
 ,
nos hemos dejado muchas “cosas en el tintero”, nos
faltan:
,
nos hemos dejado muchas “cosas en el tintero”, nos
faltan:
* Un subconjunto Ci
de un conjunto C, Ci![]() C,
es aquel en el que todos sus elementos están en el conjunto
original C. Matemáticamente decir Ci
C,
es aquel en el que todos sus elementos están en el conjunto
original C. Matemáticamente decir Ci![]() C
equivale a
C
equivale a
![]() .
En Maxima la orden subsetp ({a, b, c, e},
{a, b, c, d}); devuelve false porque “e” no está
en {a, b, c, d}. Además, podemos indicar a Maxima que nos dé
el subconjunto de números pares (subset ({1, 2, 3, 4, 5,
6}, evenp);), impares (subset ({1, 2, 3, 4, 5, 6}, oddp);)
o primos (subset ({1, 2, 3, 4, 5, 6}, primep);) de un
conjunto dado.
.
En Maxima la orden subsetp ({a, b, c, e},
{a, b, c, d}); devuelve false porque “e” no está
en {a, b, c, d}. Además, podemos indicar a Maxima que nos dé
el subconjunto de números pares (subset ({1, 2, 3, 4, 5,
6}, evenp);), impares (subset ({1, 2, 3, 4, 5, 6}, oddp);)
o primos (subset ({1, 2, 3, 4, 5, 6}, primep);) de un
conjunto dado.
* Hallar las
particiones de un conjunto C. Se trata de encontrar una colección
de subconjuntos de C (C1,C2,…Ci)
que satisfacen dos propiedades: a) la unión de todos estos
subconjuntos forman el conjunto original C; b) son subconjuntos
disjuntos, es decir, no tienen elementos en común (Ci∩
Cj =Ø, es decir, no existe ningún elemento
e que verifique simultáneamente que e![]() Ci
y e
Ci
y e![]() Cj).
En Wolfram escribiendo Partition[{a, b, c, d, e, f}, 2]
devuelve [{a, b}, {c, d}, {e, f}], es decir, un particionado con
subconjuntos de cardinalidad 2. En Maxima, set_partitions({a, b,
c}); devuelve todas las formas de particionar dicho conjunto:
{{{a},{b},{c}},{{a},{b, c}},{{a, b},{c}},{{a, b ,c}},{{a, c},{b}}}.
Cj).
En Wolfram escribiendo Partition[{a, b, c, d, e, f}, 2]
devuelve [{a, b}, {c, d}, {e, f}], es decir, un particionado con
subconjuntos de cardinalidad 2. En Maxima, set_partitions({a, b,
c}); devuelve todas las formas de particionar dicho conjunto:
{{{a},{b},{c}},{{a},{b, c}},{{a, b},{c}},{{a, b ,c}},{{a, c},{b}}}.
* En Maxima podemos comprobar: si un elemento pertenece a un conjunto: elementp(7, {2, 4, 6, 8, 10}); devuelve false, falso porque 7 no está en {2, 4, 6, 8, 10}); si un conjunto es vacío (C=Ø), así emptyp({a, b, c}); es falso porque tiene tres elementos, sin embargo, emptyp({}); es cierto; si lo que pasamos como argumento es o no un conjunto: setp(makelist(fib(n), n, 1, 10)); y setp(3) devuelven falso pero setp(miConjunto) es verdadero.
* Relaciones de
equivalencia. Una relación R de un conjunto C es un
subconjunto de C x C. Si (x, y)
![]() R decimos que están relacionados y se expresa como x R y. Una
relación R es de equivalencia si cumple las siguientes
propiedades:
R decimos que están relacionados y se expresa como x R y. Una
relación R es de equivalencia si cumple las siguientes
propiedades:
- Reflexiva: todo
elemento está relacionado consigo mismo, x R x.
Formalmente:
![]() C,
x R x.
C,
x R x.
- Simetría:
si un elemento “x” está relacionado con otro
“y”, x R y, entonces éste último
está relacionado con el primero, y R x:
![]() C,
x R y
C,
x R y
![]() R
x.
R
x.
- Transitiva: si un elemento
“x” está relacionado
con un elemento “y”, y éste además tiene
la fortuna o la desgracia, tal como se mire, de estar relacionado
con un tercero “z”, entonces el primero está
relacionado con el tercero “z”, x R z:
![]() C,
x R y, y R z
C,
x R y, y R z
![]() R
z. La transitividad es como este ejemplo: mi hija Marta le echa
la culpa a su hermano Javi sobre una travesura y éste a su
hermano gemelo Máximo, al final, los tres quedan castigados
por mamá
R
z. La transitividad es como este ejemplo: mi hija Marta le echa
la culpa a su hermano Javi sobre una travesura y éste a su
hermano gemelo Máximo, al final, los tres quedan castigados
por mamá![]() .
.
* Clases de
equivalencia. Una relación de equivalencia define en un
conjunto clases de equivalencias que no son más que
subconjuntos disjuntos de él formados por elementos que están
relacionados. Así, si a es un elemento, la clase de
equivalencia a se representa como [a] y es igual a {e
![]() C:
a R e}. Podemos solicitar en Maxima que nos defina de un
conjunto las clases de equivalencia definidas por la relación
ser primo: equiv_classes ({1, 2, 3, 4, 5, 6, 7, 8, 9, 10},
lambda([x,y], is (equal (primep(x),primep(y))))); devuelve
{{1,4,6,8,9,10},{2,3,5,7}}, es decir, el primer conjunto
{1,4,6,8,9,10} son los elementos que no son primos y {2,3,5,7} los
que sí lo son.
C:
a R e}. Podemos solicitar en Maxima que nos defina de un
conjunto las clases de equivalencia definidas por la relación
ser primo: equiv_classes ({1, 2, 3, 4, 5, 6, 7, 8, 9, 10},
lambda([x,y], is (equal (primep(x),primep(y))))); devuelve
{{1,4,6,8,9,10},{2,3,5,7}}, es decir, el primer conjunto
{1,4,6,8,9,10} son los elementos que no son primos y {2,3,5,7} los
que sí lo son.
Hemos definido la relación de equivalencia con una función
anónima (sin haber sido bautizada con un nombre como Dios
manda, “se condenará al fuego eterno por apóstata” )
definida de la siguiente forma: lambda([x,y], is (equal
(primep(x),primep(y))). La función tiene dos argumentos:
x, y. Devuelve verdadero si es igual el resultado de primep(x) y
primep(y), es decir, si ambos son primos o ninguno de ellos lo son.
)
definida de la siguiente forma: lambda([x,y], is (equal
(primep(x),primep(y))). La función tiene dos argumentos:
x, y. Devuelve verdadero si es igual el resultado de primep(x) y
primep(y), es decir, si ambos son primos o ninguno de ellos lo son.
Razonando análogamente equiv_classes ({1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, lambda([x,y], is (equal (oddp(x),oddp(y))))); devuelve {{1,3,5,7,9},{2,4,6,8,10}, es decir, la relación de equivalencia ser impar crea en nuestro conjunto dos clases: la de los números impares y la de los números pares. Véase en la figura inferior un ejemplo más elaborado y elegante en cuatro pasos:
1. Definimos miLista con los diez primeros números de la serie de Fibonacci.
2. Creamos un conjunto con setify a partir de dicha lista.
3. Definimos la relación de equivalencia R “ser primo”.
4. Solicitamos a Maxima todas las clases de equivalencia definidas en miConjunto con dicha relación de equivalencia R, es decir, el conjunto cociente. Un pequeño detalle, para Maxima 1 no es primo.

El
siguiente ejemplo es un poco más complicado, aunque los
primeros dos pasos son bien sencillos. Tomamos una lista del 1 al 20
y la convertimos en un conjunto. R es ahora la relación de
congruencia módulo 4 (en realidad puedes sustituir 4 por
cualquier otro número),
![]() (mod
4) si el resto del cociente entre a-b y 4 es cero, es decir, 4 divide
exactamente a “a-b”. Utilizamos la función de
Maxima remainder que devuelve el resto de la división
entre los dos enteros que se le pasan como argumento.
(mod
4) si el resto del cociente entre a-b y 4 es cero, es decir, 4 divide
exactamente a “a-b”. Utilizamos la función de
Maxima remainder que devuelve el resto de la división
entre los dos enteros que se le pasan como argumento.
Las
relaciones de congruencia son relaciones de equivalencia. Veamos que
los resultados son consistentes. Por ejemplo
![]() (mod
4), pues 5-17=-12 que al dividirlo con 4 da resto 0. Lo mismo sucede con
(mod
4), pues 5-17=-12 que al dividirlo con 4 da resto 0. Lo mismo sucede con
![]() (mod
4), pues 4 divide exactamente a -12.
(mod
4), pues 4 divide exactamente a -12.

6.2. Peleándonos con polinomios.
Los polinomios me matan.
 ¡Tranquilo, no es para tanto! Un polinomio es una expresión
algebraica cuya expresión general es la siguiente:
P(x)=anxn+an-1xn-1+…a2x2+a1x1+a0.
Ejemplos son: x3+35x+17 y x2-4x+4. Un polinomio
tiene una serie de coeficientes: an, an-1,…,
a2, a1, a0 y decimos que es la suma
de varios monomios o términos del polinomio. Por ejemplo, el
polinomio x3+35x+17 es la suma de tres monomios, a saber:
x3, 35x, 17. Como la mayor potencia de los monomios que lo
componen es tres, el grado del polinomio es tres.
¡Tranquilo, no es para tanto! Un polinomio es una expresión
algebraica cuya expresión general es la siguiente:
P(x)=anxn+an-1xn-1+…a2x2+a1x1+a0.
Ejemplos son: x3+35x+17 y x2-4x+4. Un polinomio
tiene una serie de coeficientes: an, an-1,…,
a2, a1, a0 y decimos que es la suma
de varios monomios o términos del polinomio. Por ejemplo, el
polinomio x3+35x+17 es la suma de tres monomios, a saber:
x3, 35x, 17. Como la mayor potencia de los monomios que lo
componen es tres, el grado del polinomio es tres.
6.2.1. Operaciones con polinomios.
|
|
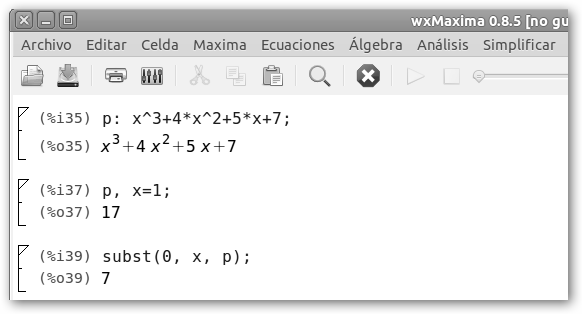
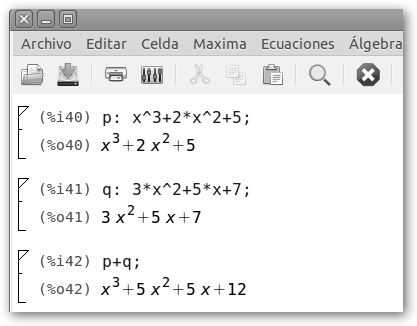
Definimos el polinomio y solicitamos el valor del polinomio en 1 y en 0, es decir, el resultado de sustituir la variable x por 1 y por 0. Se puede utilizar el operador coma “,”con la función subst o desde el menú Simplificar, Sustituir. Por ejemplo: P(1)=13+4*12+5*1+7=1+4+5+7=17. |
|
Vemos con wxMaxima como realizamos la suma de dos polinomios. Observa como sumamos los coeficientes de los términos que tienen el mismo grado.
|
|
|
|
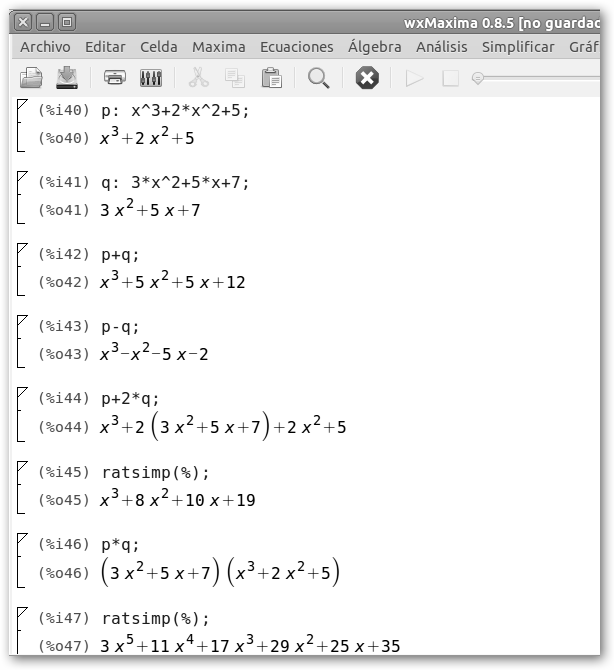
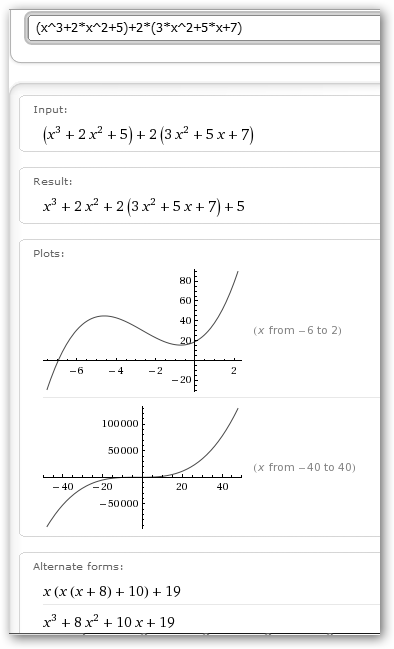
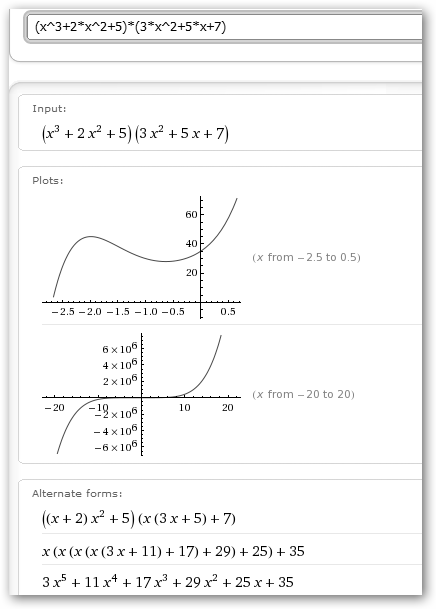
Realizamos además la resta de los dos polinomios, así como, P(x)+2*Q(x) y la multiplicación de los dos polinomios. Fíjate que tenemos que llamar a la función ratsimp(%) para simplificar la expresión resultante o desde Simplificar, Simplificar expresión.
En la multiplicación de polinomios multiplicamos todos los términos de un polinomio (Q(x)) por los del otro (P(x)) y se simplifican los términos semejantes. |
|
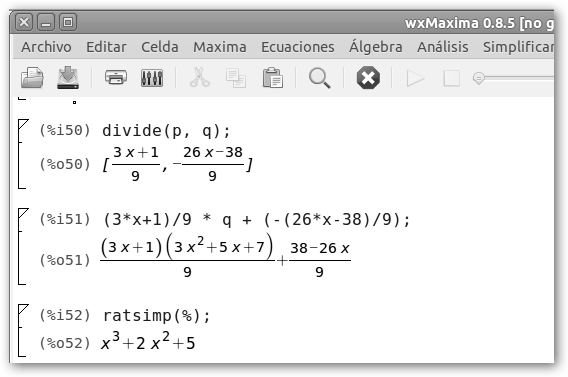
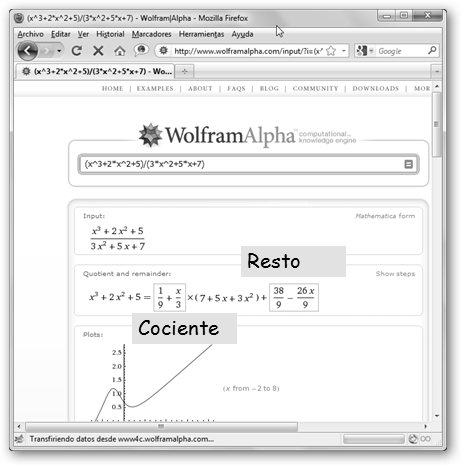
Con la orden divide o desde el menú Análisis, Dividir polinomios podemos dividir dos polinomios. Obtenemos el cociente y el resto. Se ilustra también en la figura la comprobación de la división: Dividendo (P(x)) = Cociente * Divisor (Q(x)) + Resto. |
|
|
|
Con WolframAlpha podemos también realizar todas las operaciones con polinomios.
En la sección Alternate forms obtenemos la versión simplificada de los resultados. |
6.2.2. Expresiones notables.
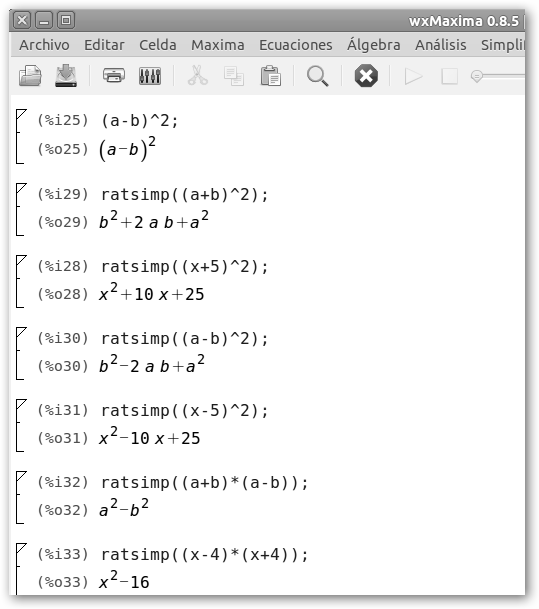
Es importante recordar estas
expresiones notables para salvarnos tiempo, ¡sobre todo en los exámenes!
 En WolframAlpha tendrás los mismos resultados en la
sección Alternate forms.
En WolframAlpha tendrás los mismos resultados en la
sección Alternate forms.
6.2.3. Factorización de polinomios
|
|
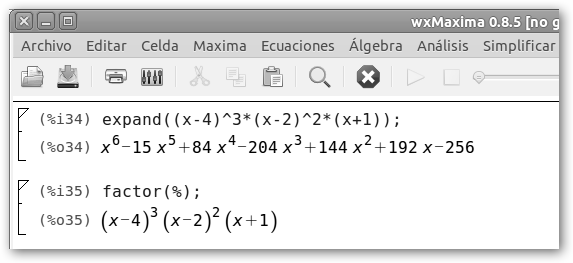
Para expandir una expresión en wxMaxima utilizamos la orden expand o desde el menú Simplificar, Expandir expresión. Para factorizar un polinomio (expresarlo como producto de binomios, es decir, con dos términos) contamos con la función factor o la opción Factorizar expresión del menú Simplificar. |
|
Por supuesto, tenemos como siempre nuestro aliado WolframAlpha. |
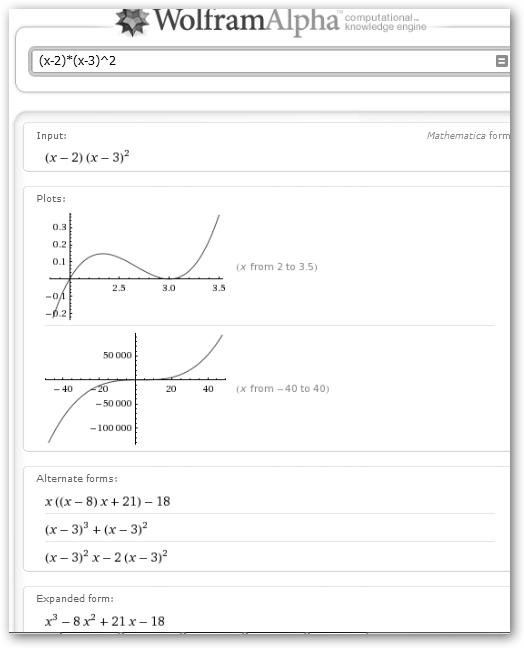
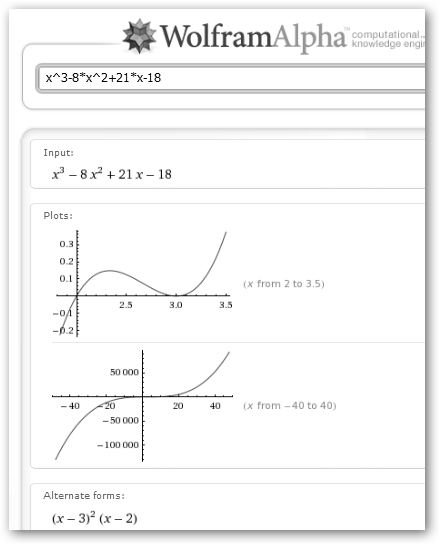
Observa los detalles de la expansión de una expresión (Expanded form) así como de la factorización de un polinomio (Alternate form). |
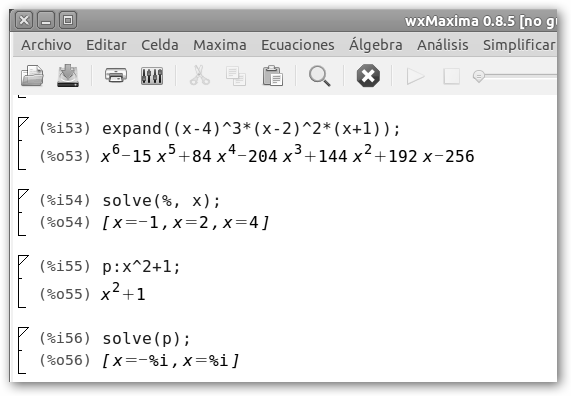
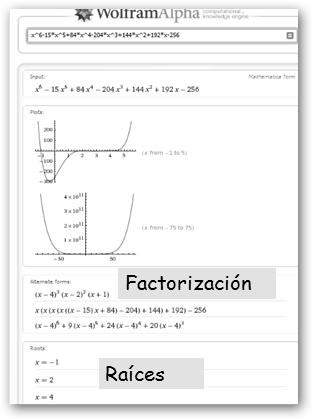
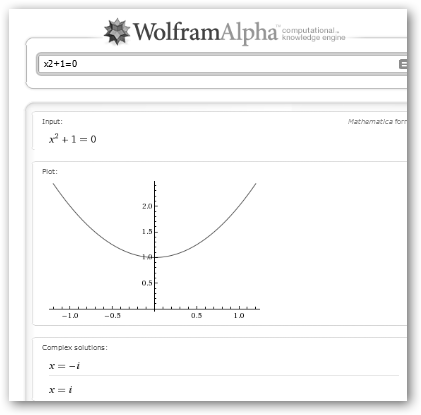
6.2.4. Raíces de un polinomio.
|
Para calcular las raíces de un polinomio utilizamos la función solve o navegamos por Ecuaciones, Resolver. Comprueba que encuentra las raíces complejas de x2+1. En WolframAlpha si introducimos un polinomio nos devuelve la representación gráfica, su factorización, las raíces, etc. ¡Parece que le han dado cuerda con tanta información! |
|
6.2.5. La regla de Ruffini
|
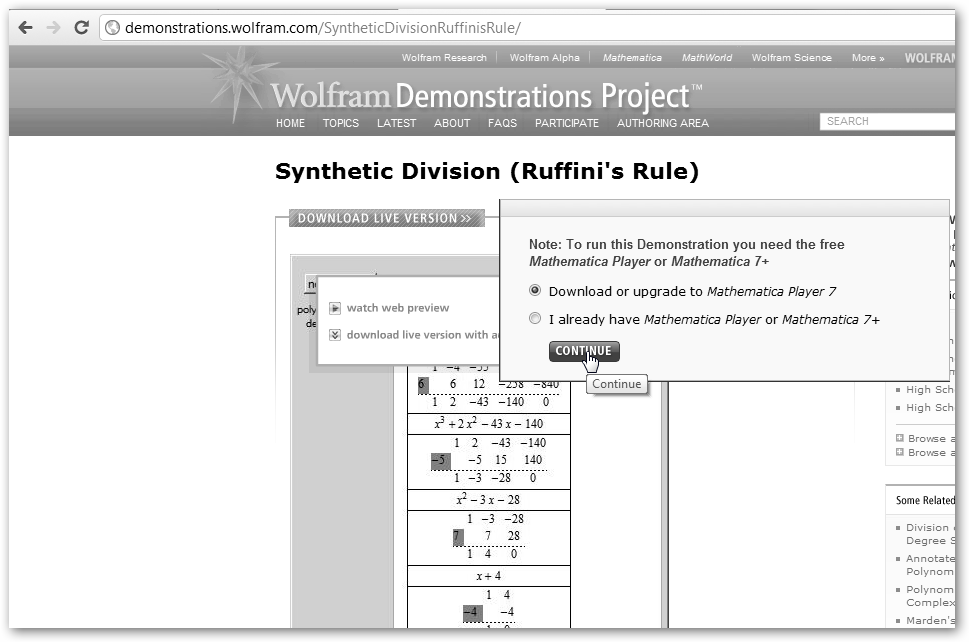
En demonstrations.wolfram.com/ SyntheticDivisionRuffinisRule encontrarás una demostración de la famosa regla de Ruffini. Haz clic en Download Live Version para descargar e instalar el programa gratuito Mathematica Player 7, luego pulsa en Download or upgrade to Mathematica Player 7 y en CONTINUE. |
|
Te pedirá tu nombre, e-mail, organización (teclea típicamente Casa), afiliación, ámbito de interés, sistema operativo, así como, responder a una pregunta para comprobar que no eres un robot. Suministra estos datos para poder descargar la herramienta y haz clic en DOWNLOAD NOW, descargar ahora. ¡Ojo!, estás descargando la versión Player de Mathematica, no el Mathematica en sí que cuesta sobre unos 3.000 euros.
|
Una vez lanzado haz clic en FIND DEMONSTRATIONS para buscar demostraciones y ejemplos en Wolfram Demonstrations Project. |
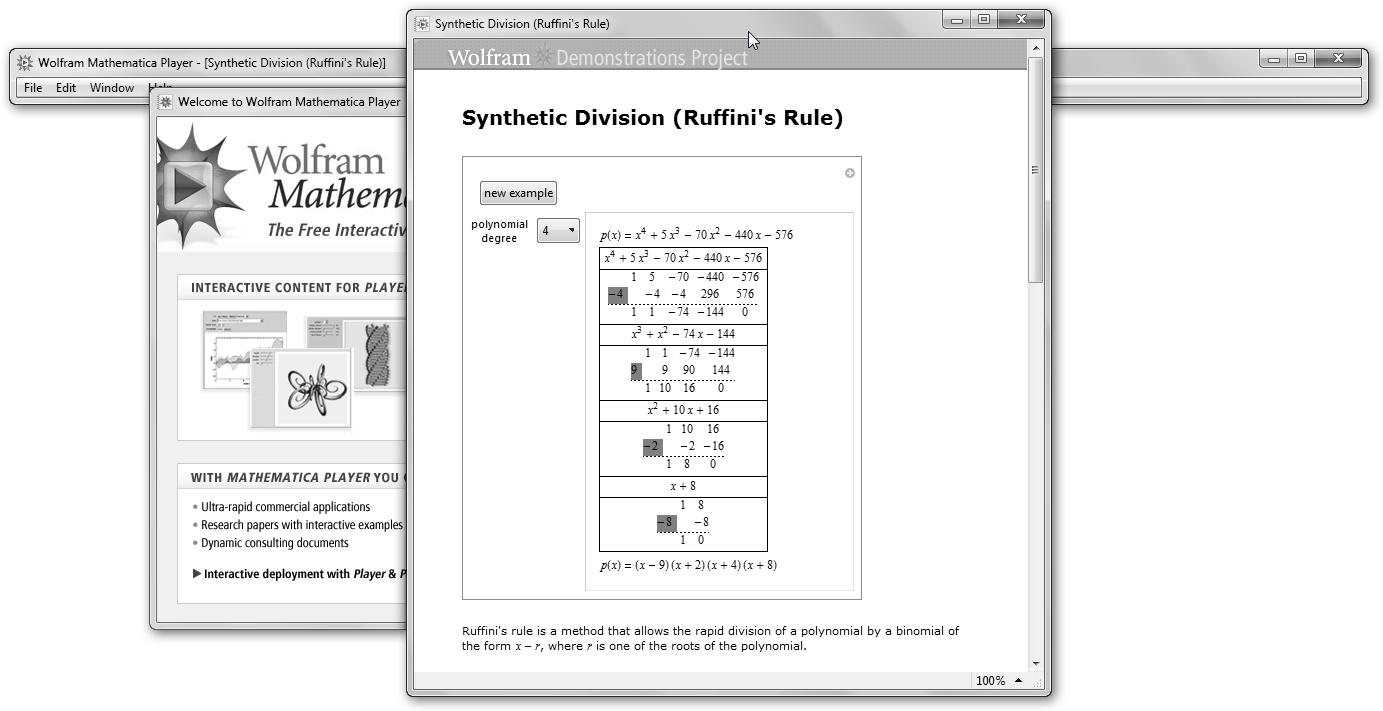
Vuelve a la misma página y pulsa en Download Live Version. Haz doble clic en el archivo .nbp descargado y podrás visualizar numerosos ejemplos de aplicación de la regla de Ruffini pulsando en new example. |
|
Se ilustran dos demostraciones más: resolución de una ecuación con una incógnita y de una ecuación de segundo grado. Hay cientos de ejercicios, los inconvenientes son que hay que buscarlos y que están en inglés. |
Típicamente navegarás a la sección Mathematics de demonstrations.wolfram.com/ topics.html y buscarás en una categoría: School Mathematics (matemáticas elementales), Algebra (algebra), Geometry (geometría), etc. |
6.3. Ecuaciones de primer grado.
Una ecuación es una igualdad entre dos expresiones algebraicas que contiene una o más incógnitas y que se puede verificar para ciertos valores de dichas incógnitas, por ejemplo: x3+2*x*y=3*x+y2, 4*y3+7* y=6*x2+y3. Una ecuación de primer grado es aquella en la que la única incógnita x tiene como exponente 1, es decir, no está elevada a ninguna potencia.
Supongamos el siguiente problema: si el doble de los patitos que tengo más seis es igual al número de mis patitos menos cuatro. ¿Cuántos patitos tengo?
Sería 2 *
 + 6 =
+ 6 =
 -4. Sustituyendo los patitos por la incógnita x tendremos una
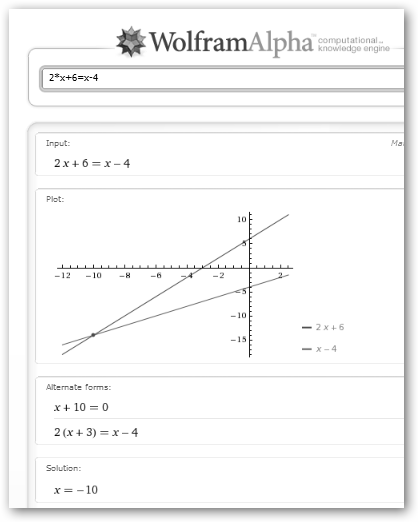
ecuación matemática: 2*x+6=x-4. Lo resolveremos primero
en Maxima y luego en WolframAlpha.
-4. Sustituyendo los patitos por la incógnita x tendremos una
ecuación matemática: 2*x+6=x-4. Lo resolveremos primero
en Maxima y luego en WolframAlpha.
|
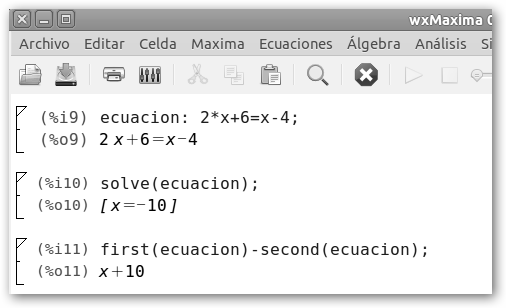
|
Considera lo siguiente: 1. Como se define la ecuación de primer grado: ecuacion: 2*x+6=x-4; (¡ecuacion sin tilde!). 2. La resolución de la ecuación se solicita con solve(ecuación) o desde el menú Ecuaciones, Resolver. 3. El primer miembro de la ecuación sería first(ecuación)(en el ejemplo, x) y el segundo second(ecuación) (-10). |
||
|
|
Como se observa en la figura al teclear en WolframAlpha la ecuación, obtenemos la representación gráfica de los dos miembros de la ecuación tal como se escribieron. Se trata de dos rectas: 2x+6, x-4 que se cortan en x=-10. Por supuesto, donde ambas rectas se encuentran es la solución de la ecuación. Sin embargo, a veces, no somos tan afortunados. No todas las ecuaciones tienen soluciones e incluso algunas tienen infinitas soluciones, es decir, algunas se pasan y otras no llegan. |
||
|
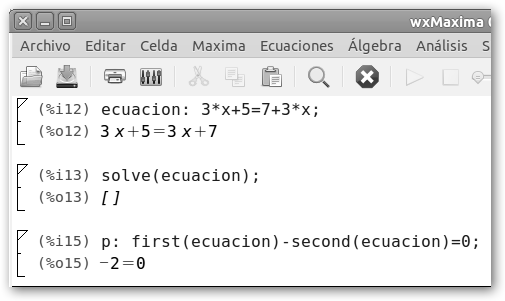
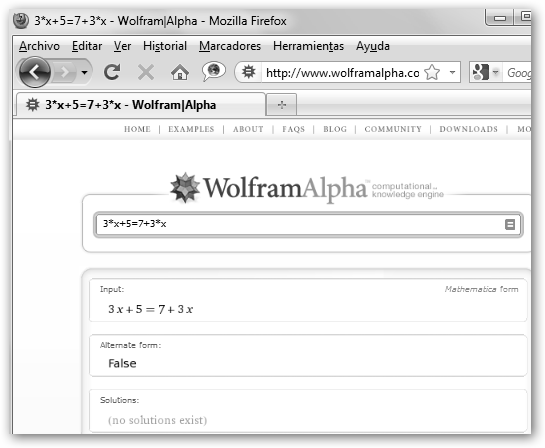
Por ejemplo 3x+5=3x-7, es igual a 3x-3x=-7+5, es decir, 0=2. Por supuesto ningún valor podrá satisfacer dicha ecuación. |
Observa como Maxima dice que la lista de soluciones es la lista vacía [] y WolframAlpha indica: no solutions exist, no existen soluciones. |
||
|
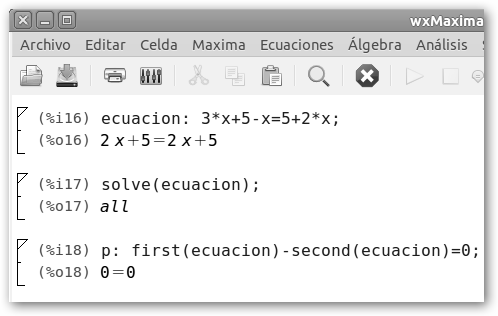
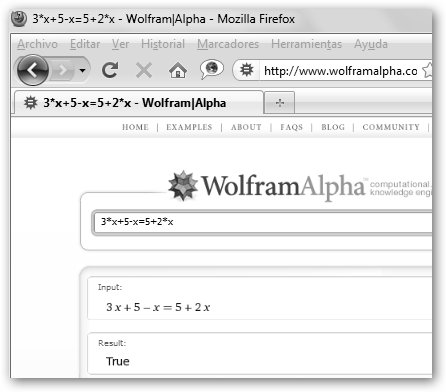
En el lado opuesto, 3x+5-x=5+2x es igual a 3x-x-2x=5-5, es decir, 0=0, por tanto cualquier número con el que se sustituya la incógnita x (all) verifica la ecuación. |
Wolfram lo expresa diciendo que es True. |
||
|
Veamos un último ejemplo: ¿Cuánto tardó cada cerdito en construirse su casa en la famosa fábula?
Entre todos tardaron 17 años. El más pequeño
lo hizo en un “santiamén” pues era de paja,
¿recuerdas? (sea x el tiempo que tardó). Cuando el
lobo feroz destruyó la casa de un fuerte soplido
|
La ecuación se muestra en la ilustración y es 3x+14=17, la solución es 1. Por tanto, el pequeño sólo tardó un año, el mediano necesitó 3 y el mayor 13. Lo cual no fue una excesiva buena idea, las dos primeras fueron derrumbadas por el lobo y para la tercera, el mayor quedó tan endeudado al construirla que el banco la embargó y ahora viven de nuevo en la casa de sus padres.
|
6.4. Ecuaciones de segundo grado.
|
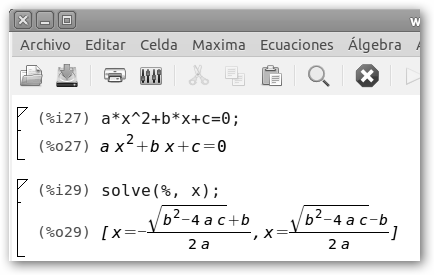
Una ecuación de segundo grado es aquella en la que la única incógnita x tiene como máximo exponente 2. Se expresa como ax2+bx+c y se resuelve cómo se muestra en la figura: |
|
|
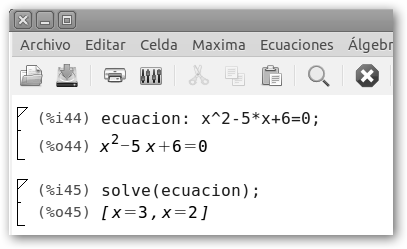
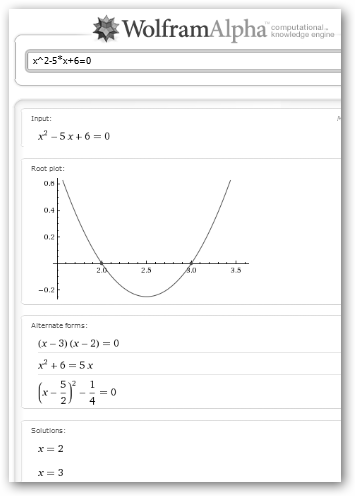
Existen varias posibilidades. A.Que el discriminante b2-4ac sea mayor que cero y tengamos dos raíces reales. En el ejemplo, el discriminante b2-4ac= 52-4*1*6=1>0. La raíz cuadrada del discriminante son 1 y -1. Las soluciones son: * X1 = (5-1)/2 = 2. * X2 = (5+1)/2 =3. La representación gráfica de la ecuación de segundo grado es una parábola que corta al eje de abscisas en los puntos x=2 y x=3. |
Fíjate que tanto para Maxima (solve) como para WolframAlpha la petición de resolución se hace de la misma forma que para ecuaciones de primer grado. |
|
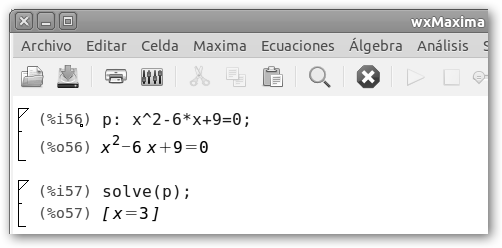
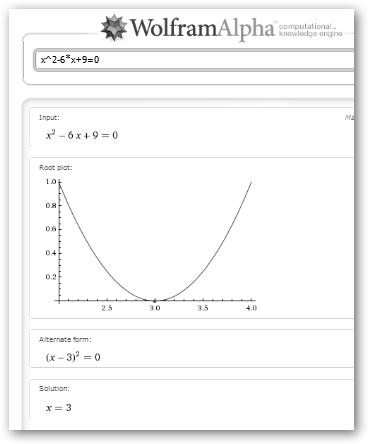
B. El discriminante b2-4ac sea igual a cero y tengamos únicamente una única raíz.
En el ejemplo b2-4ac= 62-4*1*9=0 cuyo raíz cuadrada es cero patatero. Las soluciones son: * X1 = (6-0)/2=3. * X2 = (6+0)/2=3. Es decir, una única solución que es el único punto en el que la parábola interseca con el eje de abscisas. |
|
|
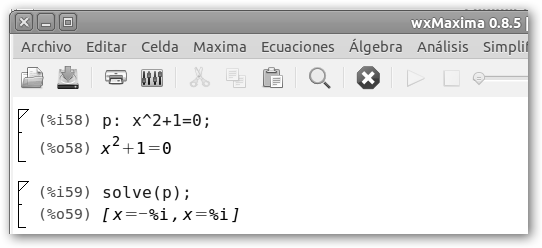
C. El discriminante b2-4ac = 02 -4 * 1 *1 = -4<0 es menor que cero, por lo tanto no tiene raíces reales. En la representación gráfica observa que la parábola no interseca con la recta real. Si tenemos, sin embargo, dos soluciones imaginarias –i, i. |
|
6.5. Sistemas de dos ecuaciones con dos incógnitas.
Un sistema de ecuaciones es un conjunto o una lista de ecuaciones.
Existen tres métodos de resolución: sustitución,
igualación y reducción. ¿Para qué
 queremos los sistemas de ecuaciones? Existen miles de problemas que
sólo podrás resolver con un sistema de ecuaciones, por
ejemplo, recuerdas el que planteamos al principio:
queremos los sistemas de ecuaciones? Existen miles de problemas que
sólo podrás resolver con un sistema de ecuaciones, por
ejemplo, recuerdas el que planteamos al principio:
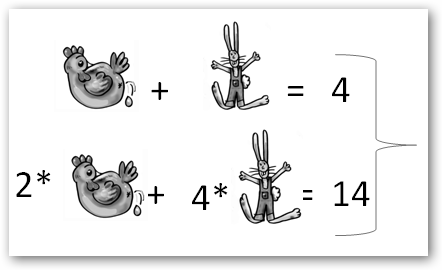
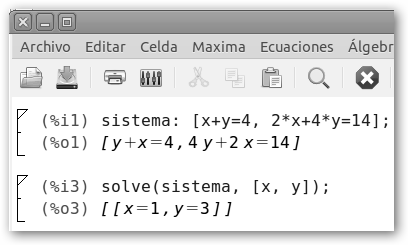
En un corral hay conejos y gallinas. El total de las cabezas suman 4 y el número de patas es 14. ¿Cuántos conejos hay? ¿Y gallinas? Entonces lo resolvimos por reducción, ahora lo haremos por sustitución.
|
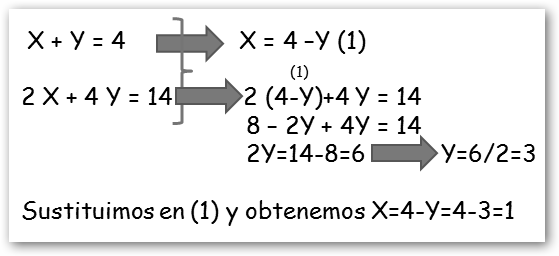
El método de sustitución consiste básicamente en despejar una incógnita (X) de una de las ecuaciones (X=4-Y) y sustituir la expresión resultante en la segunda ecuación (2(4-Y)+4Y=14) para poder resolverla (Y=3). |
Si sustituimos las gallinas por X y los conejos por Y tenemos el siguiente sistema de ecuaciones: 1. X + Y = 4 2. 2 X + 4 Y = 14.
|
|
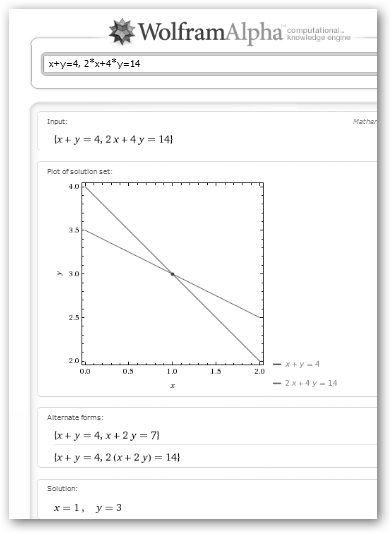
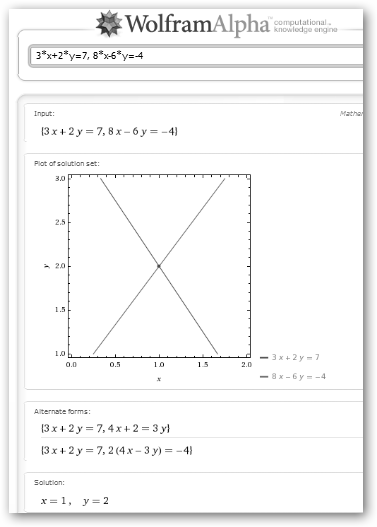
En Wolfram basta con separar las ecuaciones con comas “,”. Fíjate como ambas rectas se cortan en (1, 3). |
Ahora solicitamos a Maxima y WolframAlpha que la resuelva y podamos comprobar que hemos realizado correctamente los cálculos. Observa la sintaxis para definir el sistema en Maxima: sistema: [ecuación1, ecuación2]. Luego para resolverlo escribe solve(sistema, [x, y]), es decir, el sistema de ecuaciones, una coma y la lista de incógnitas entre corchetes y separadas por comas. |
|
|
Es importante reconocer que cada día que pasa es más importante la definición y conceptualización del problema, la interpretación de los resultados que la computación, en este caso, la resolución del sistema de ecuaciones en sí. Para esta tarea, las máquinas son más rápidas y mejores que nosotros. La parte previa es la creativa, la más puramente humana. |
|
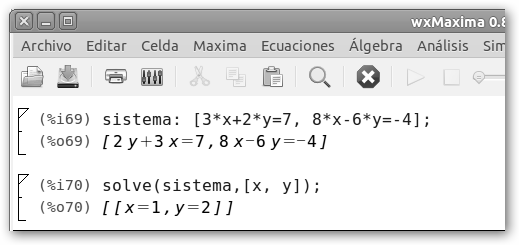
En este otro ejemplo proponemos otro sistema de ecuaciones: 1. 3*X + 2*Y = 7 2. 8*X – 6*Y = -4. Comprueba que tanto Maxima como WolframAlpha encuentran que la solución es un único punto: x=1, y = 2. La ventaja de WolframAlpha es que te muestra además de la solución, la representación gráfica, la desventaja es que necesitas de conexión a Internet. |
¡No te
equivoques!, no todos los sistemas de ecuaciones tienen una única
solución, existen algunas más malignas
|
|
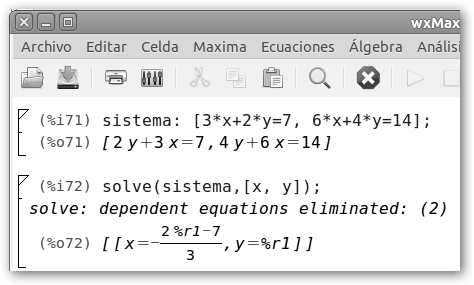
Observa el sistema de la figura. No tiene una única solución porque tenemos una ecuación redundante, más concretamente si multiplicamos la primera ecuación (3*X+2*Y=7) por 2, obtenemos la segunda (6*X+4*X+14). Por tanto, tiene infinitas soluciones tantas como puntos hay en la recta que define la ecuación 3*X+2*Y=7. Maxima sugiere que tomes un “y” al azar (%r1), digamos 1, x=-(2*1-7)/3=5/3. (5/3, 1) verifica la ecuación 3*X+2*Y=7: 3*5/3 + 2*1=5+2=7. |
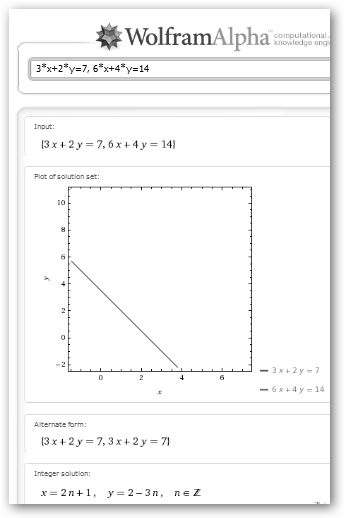
Wolfram dice toma “n” cualquier número entero, pongamos 1. x=2*n+1= 2*1+1=3; y=2-3n=2-3*1=-1. Luego (3, -1) satisfacen 3*X+2*Y=7: 3*3+2*(-1)=9-2=7. |
|
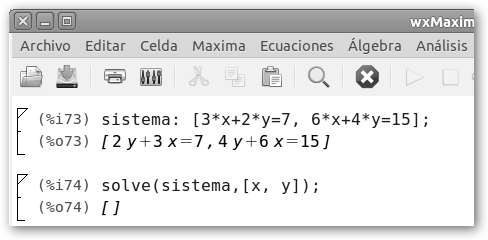
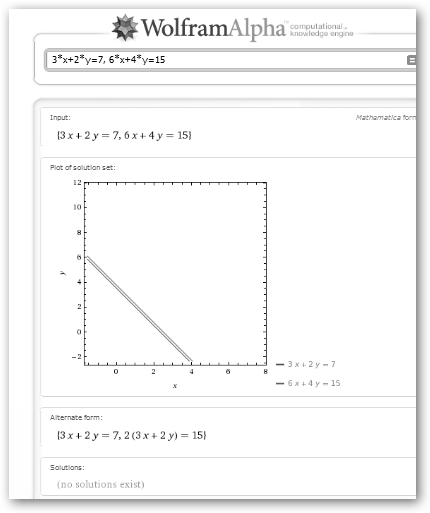
También existen sistemas donde no hay soluciones. Observa la figura. Multiplica la primera ecuación por dos y obtendrás 6*X+4*Y=14. La segunda ecuación es 6*X+4*Y=15. Si restamos las segunda ecuación a la primera obtenemos 0 =15-14, es decir 0=1. Se trata, por tanto, de dos rectas paralelas que no se cortan en ningún punto. |
|
6.6. Inecuaciones
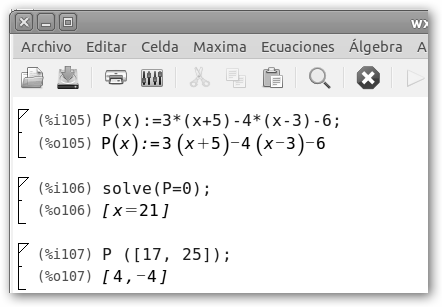
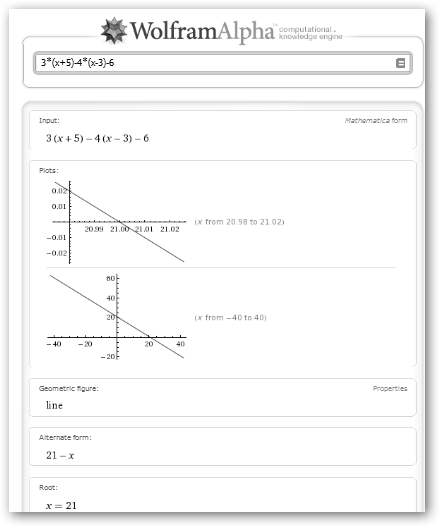
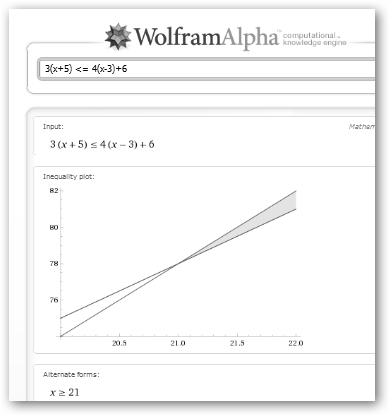
Las inecuaciones son expresiones que presentan desigualdades algebraicas, por ejemplo: 3(x+5) <= 4(x-3)+6, 2 x > 14, etc. Wolfram Alpha te permite escribirlas tal cual y en la sombra bordeada tendrás la solución: x>=21.
|
En Maxima podemos aplicar un pequeño truco. Si por ejemplo la inecuación es 3(x+5) <= 4(x-3)+6, podemos resolverlo con los siguientes pasos: 1. Pasamos el miembro de la derecha a la izquierda. 2. Resolvemos el polinomio resultante con solve como siempre. 3. Comprobamos que en (-∞, 21) el polinomio es positivo, pues en 17 (un punto arbitrario) lo es (4>0) y en (21, +∞) negativo (en 25 lo es, -4<0). Por tanto, la solución es donde el polinomio es negativo (P(x)<=0): x>=21 (21, +∞). |
WolframAlpha te permite visualizar más claramente los mismos resultados. Esto es un punto muy importante a su favor, en su contra está que no es software libre, sólo gratuito… por ahora. |
|
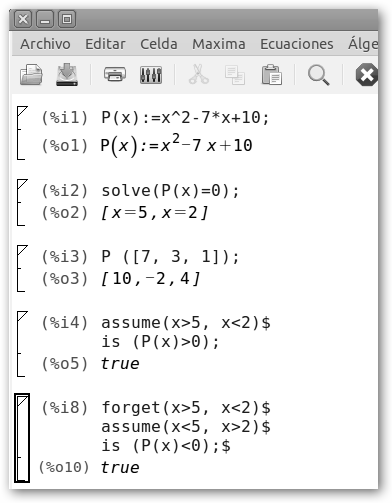
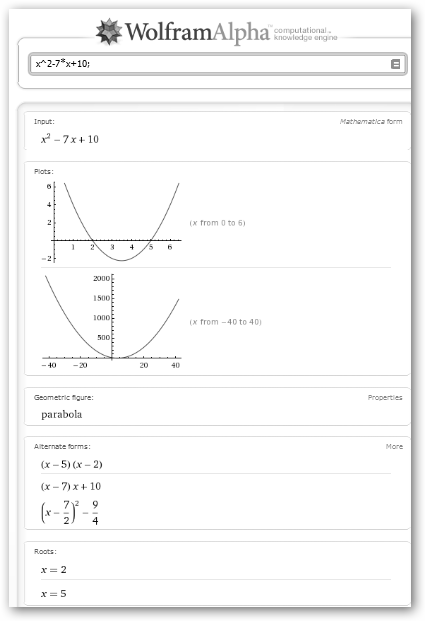
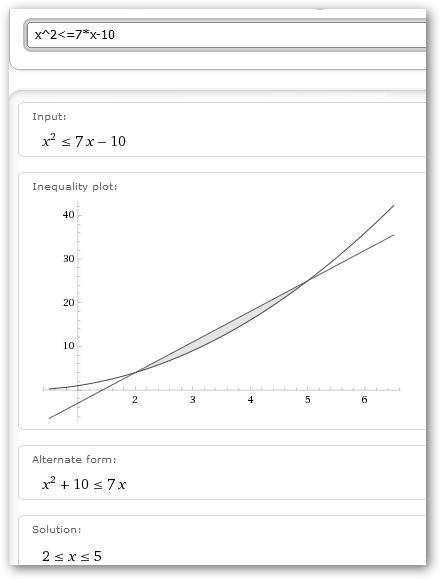
Si la inecuación es x2<=7*x-10 operamos como en el caso anterior. La diferencia es que ahora en la parábola tenemos tres zonas: dos positivas (-∞, 2), (5, +∞) y una negativa (2, 5). Lo sabemos porque hemos tomado tres puntos arbitrarios en cada zona (1, 7, 3 respectivamente) y los hemos evaluado. Luego, la inecuación se satisface en (2, 5). |
|
|
Explicaremos mejor las últimas líneas que lo único que sirven es para ser “más formales”: * assume(x>5, x<2)$: assume indica a Maxima que asumiremos como válida una condición lógica, en este caso que x sea mayor que 5 o menor que 2. * is(P(x)>0)$: preguntamos si P(x) es mayor que cero bajo dicha condición lógica y nos devuelve verdadero. * forget(x>5, x<2)$: indica a Maxima que no asuma como válida una condición lógica previa. Esto se realiza para, a continuación, buscar si el polinomio P(x) es menor que cero si x está en (2, 5). Por supuesto, si no te quieres complicar mucho la vida, ya sabes WolframAlpha es tu amigo:
|
|
 en ayuno en
un
en ayuno en
un ).
).
 .
.
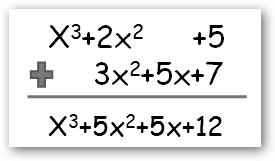
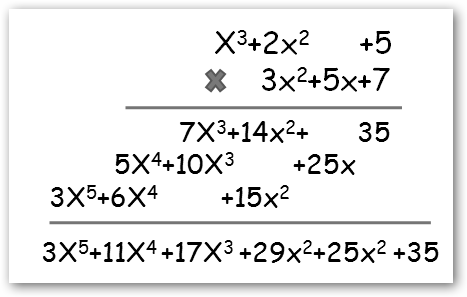


 ,
todos salieron corriendo y el mediano decidió empezar a
construir una más sólida. El mediano tardó
dos años más (x+2), su casa era de madera, su
construcción más laboriosa, pero el lobo volvió
y sopló y sopló,…, ¡y como no fumaba ni
padecía de asma!, consiguió derrumbar la segunda
casa y los tres se quedaron de patitas en la calle. El mayor muy
decidido por resolver el problema, pensó día y
noche, planificó con esmero y precisó diez años
más que el mediano pues su casa estaría construida
con ladrillos y además le costó encontrar mano de
obra y materiales (por cierto muy caros) en el tiempo de la
burbuja especulativa (x+2+10).
,
todos salieron corriendo y el mediano decidió empezar a
construir una más sólida. El mediano tardó
dos años más (x+2), su casa era de madera, su
construcción más laboriosa, pero el lobo volvió
y sopló y sopló,…, ¡y como no fumaba ni
padecía de asma!, consiguió derrumbar la segunda
casa y los tres se quedaron de patitas en la calle. El mayor muy
decidido por resolver el problema, pensó día y
noche, planificó con esmero y precisó diez años
más que el mediano pues su casa estaría construida
con ladrillos y además le costó encontrar mano de
obra y materiales (por cierto muy caros) en el tiempo de la
burbuja especulativa (x+2+10). 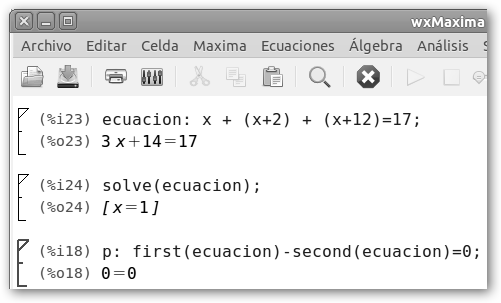



 .
.