5. Fracciones, números decimales e irracionales. ¡Ya la liamos!
5.2. Fracciones diferentes pero iguales ¿Queeeeeeeé?
5.3. Simplificación de fracciones.
5.5. Aritmética de fracciones: ¡si empezamos con nombres raros me voy!
5.6. Fracciones impropias y mixtas
5.7. Representación de las fracciones en la recta real.
5.8.1. Conversión de números decimales a fracciones.
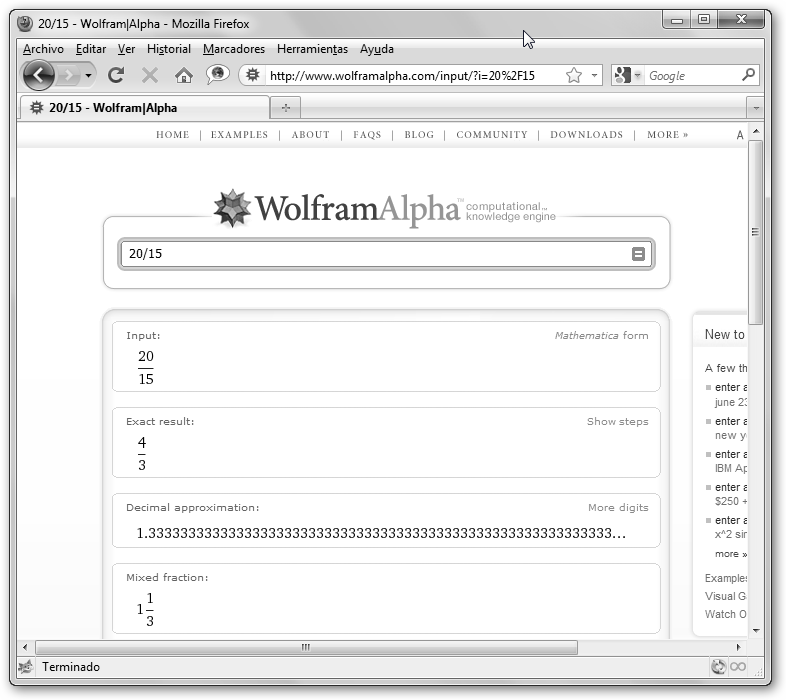
5.8.2. Conversión de fracciones a números decimales.
5.8.3. Tu primero, tu segundo,…
5.8.4. Operando con números decimales.
5.10. Números insensatos…bueno, irracionales.
5.11. Conversión entre diferentes unidades de medida.
5.12. Proporciones y la Regla de tres.
5.1 ¿Cómo se comen?

|
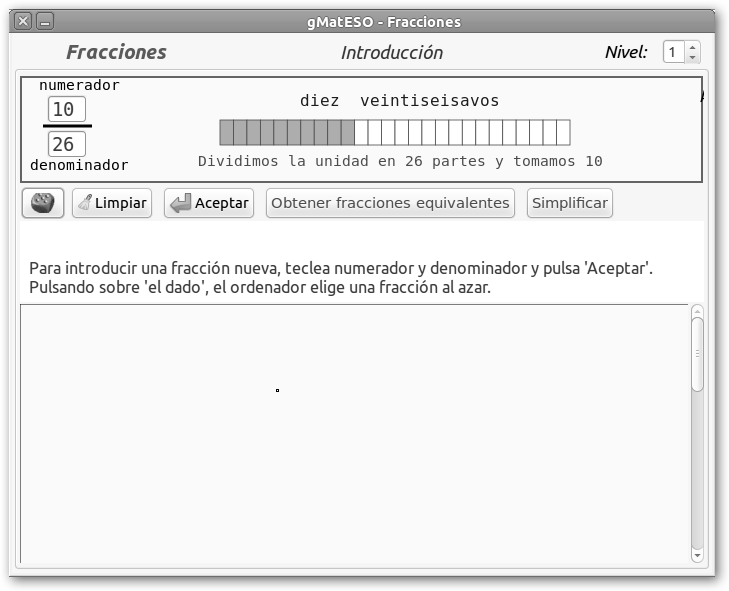
Para ver cómo se comen utilizaremos gMatESO. Lánzalo desde Aplicaciones, Educación, gMatESO. Haz clic en el menú Temas y selecciona la opción Fracciones. En la siguiente pantalla podemos seleccionar el nivel. En esta pantalla
(Nivel 1) podemos observar el concepto de fracciones. Si dividimos una tarta
o una pizza en partes iguales Al 10 lo llamamos numerador y a 26 denominador. |
|
|
|
5.2. Fracciones diferentes pero iguales ¿Queeeeeeeé?
|
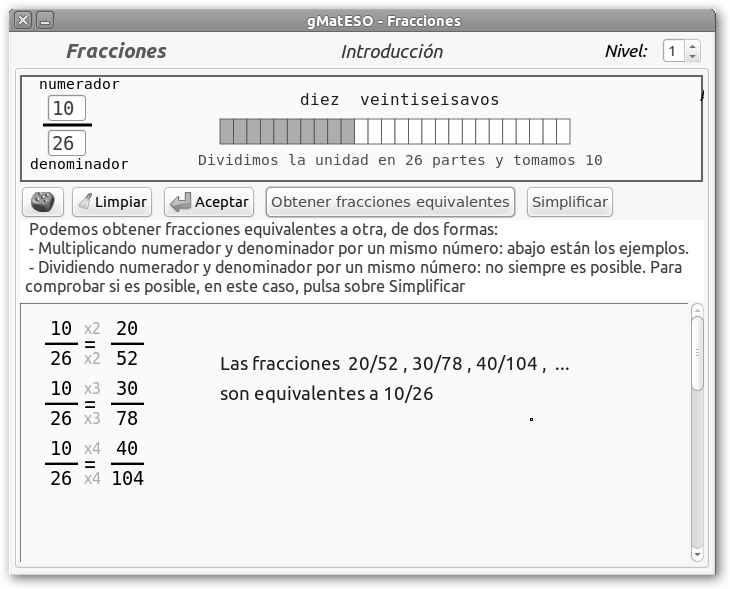
En la misma pantalla puedes hacer clic en el botón Obtener fracciones equivalentes y obtendremos 20/52, 30/78 y 40/104 al multiplicar tanto el numerador como el denominador por 2, 3 y 4 respectivamente. Dos fracciones equivalentes representan el mismo valor, aunque se escriben de forma diferente; por ejemplo, 1/2=2/4=4/8 representan lo mismo, la mitad de la pizza. |
|
|
|
|
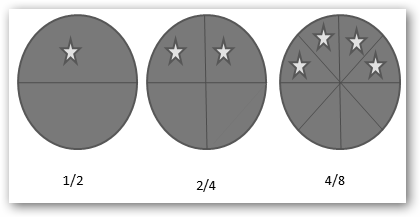
La idea es sencilla, si tienes una tarta y la divides por dos tenemos la fracción 1/2. Podemos dividir la tarta en cuatro partes, si cogemos dos, poseemos 2/4. Si la dividimos en ocho partes y tomamos cuatro, nuestra fracción es 4/8. Es decir si multiplicamos el numerador y el denominador por el mismo número siempre nos quedamos como estamos, en el ejemplo media tarta. |
|
|
|
||
5.3. Simplificación de fracciones
|
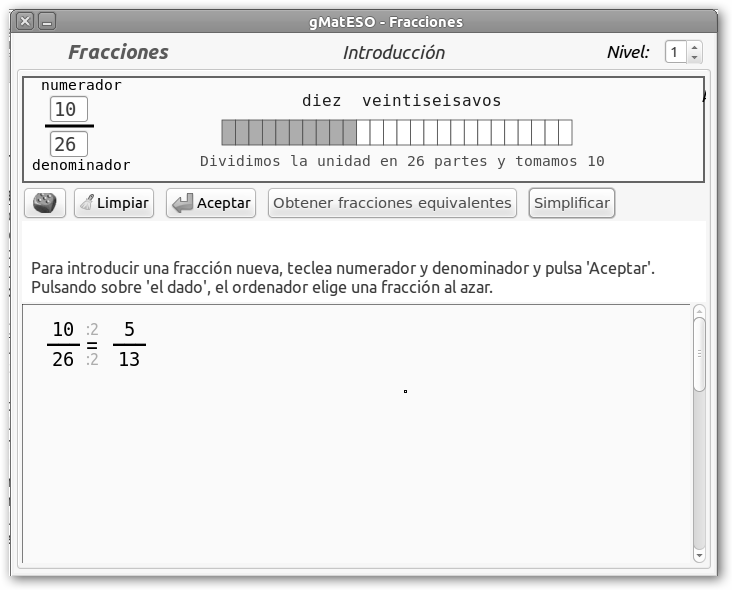
Como existen muchas fracciones equivalentes nos interesa simplificar, es decir, obtener una fracción más simple, una cuyo numerador y denominador sean los más pequeños posibles. Si dividimos el numerador y el denominador por el máximo común divisor obtenemos una fracción irreducible (5/13), es decir, que no se puede reducir por otra más pequeña. |
|
|
|
Haz clic en el botón Simplificar y obtendremos 5/13. Observa que el m.c.d(10,26) = m.c.d(2*5,2*13) = 2, por lo que dividimos 10 y 26 por 2. Intenta con 70/60, como el m.c.d(70, 60) = m.c.d(2*5*7, 22*5*3)= 2*5=10, la fracción irreducible se obtiene dividiendo 70 y 60 por 10, es decir, será 7/6. “No solo de gMatESO vive el hombre”. JFractionLab es otra magnifica herramienta para aprender fracciones. Es libre, multiplataforma y se puede descargar de sourceforge.net/projects/jfractionlab/. Necesitas tener instalado el entorno de ejecución de Java (JRE), si no lo tienes ya obtenlo de www.java.com/es/download. En Windows lo encontrarás en Inicio, Todos los programas, JFractionLab, JFL. En Ubuntu precisas el paquete jfractionlab. |
||
|
Observa todas
las actividades a tu disposición para que “seas un hacha”
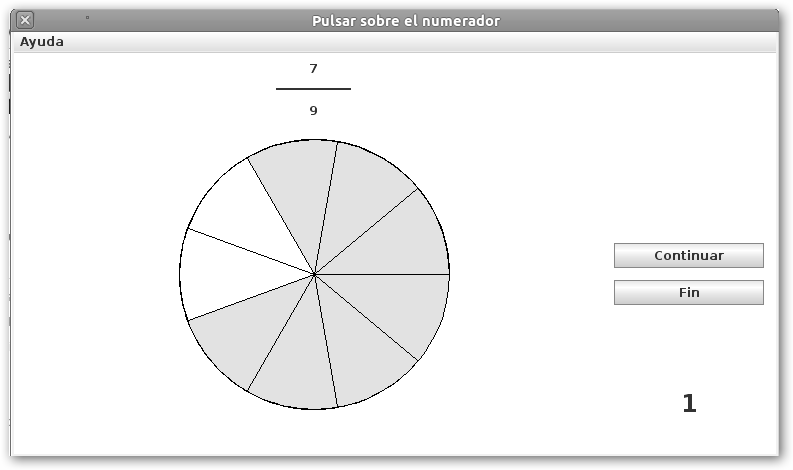
Selecciona Pulsar sobre el resultado y observa una tarta dividida en 9 quesitos (el denominador de la fracción es 9). Haz clic en tantas partes como indique tu numerador (en el ejemplo 7) y pulsa en Continuar. |
|
|
|
|
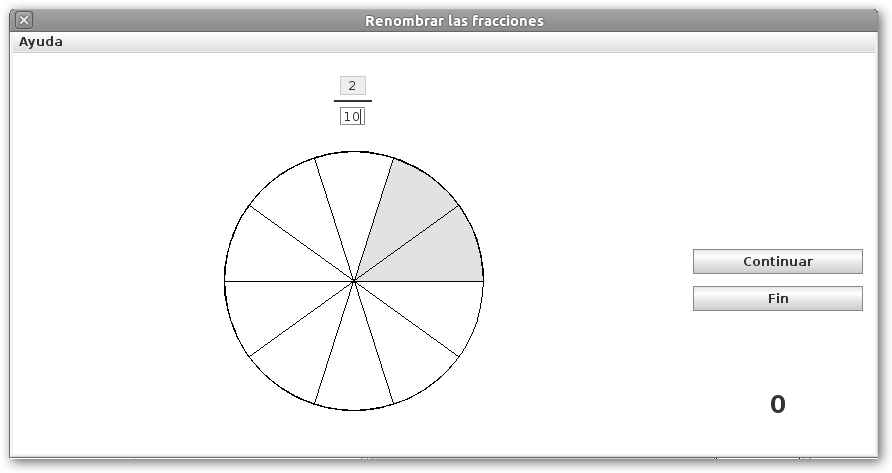
En Definir la fracción debes indicar la fracción que corresponde al dibujo. Introduce el numerador, pulsa INTRO, escribe el denominador y haz clic nuevamente en INTRO. |
|
|
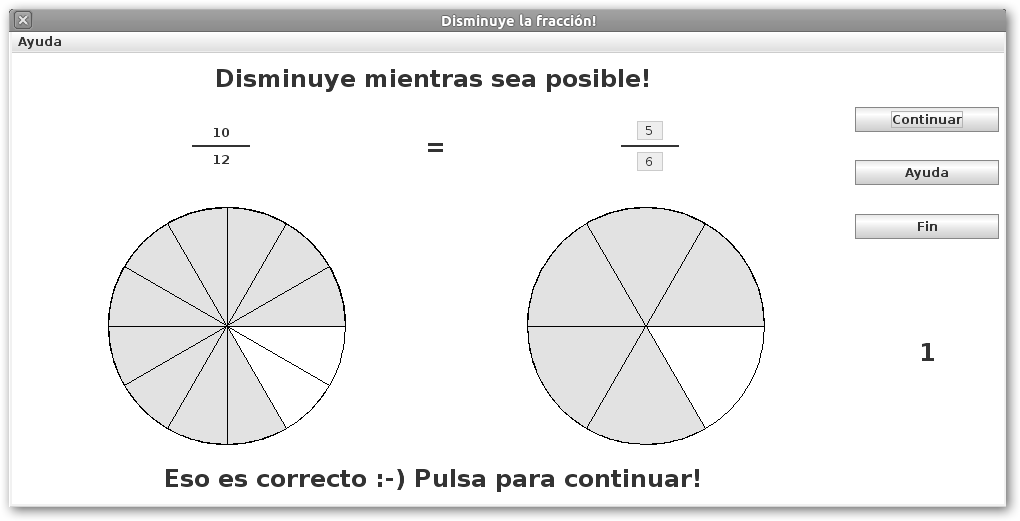
En Disminuir las fracciones aprenderemos a simplificar fracciones para obtener la fracción irreducible. 5/6 es irreducible porque m.c.d.(5, 6)=1, en otras palabras, 5 y 6 son primos entre si. |
|
|
|
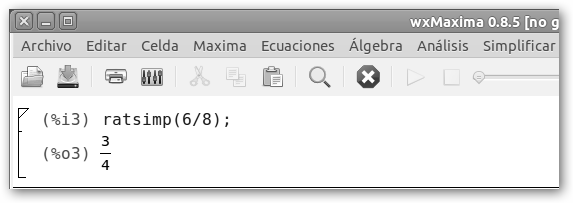
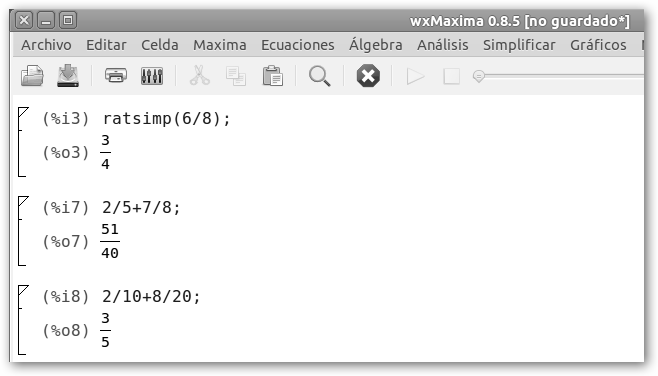
En wxMaxima podemos simplificar una fracción escribiendo ratsimp(fracción), por ejemplo, ratsimp(6/8); También puedes escribir la fracción o cualquier otra expresión más compleja y navegar por Simplificar, Simplificar expresión. |
|
|
|
Si escribimos una fracción reducible, Wolfram devolverá la fracción equivalente irreducible. Para saber cómo lo resuelve, haz clic en Show Steps. |
Comprueba que primero factoriza el numerador y el denominador, para continuar eliminando los factores comunes (5) con el mínimo exponente (1) que se presentan tanto en el numerador como en el denominador. |
5.4. Comparando fracciones.
|
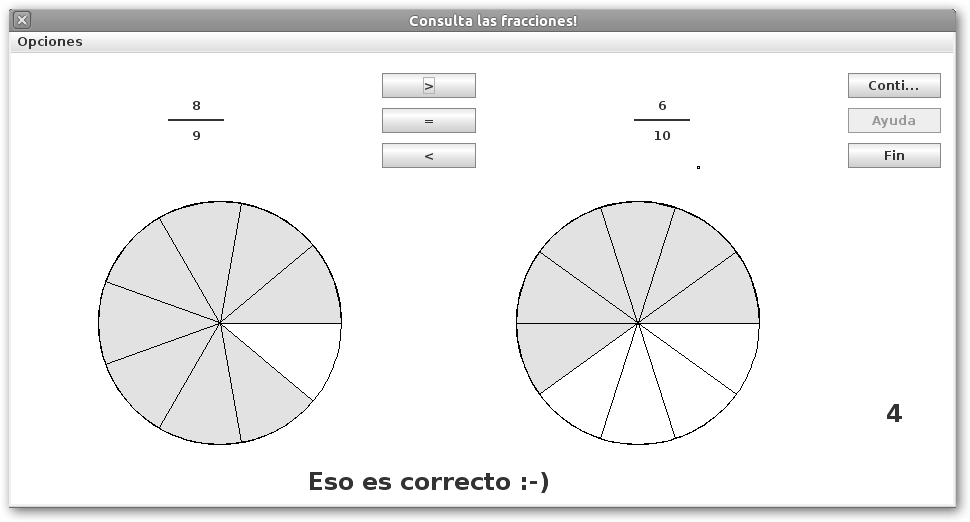
Siguiendo con JFractionLab, en la actividad Consultar las fracciones podemos comparar fracciones. Observa la importancia de la representación gráfica para que puedas resolver el problema e interpretar los resultados. |
|
|
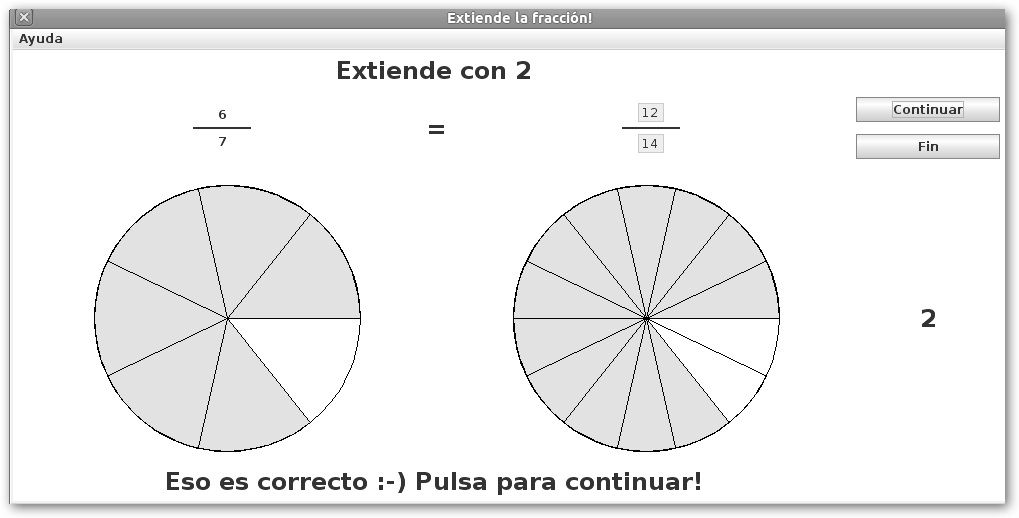
En el mismo programa, el ejercicio Extender las fracciones, nos propone obtener fracciones equivalentes más complicadas (aunque son en realidad lo mismo), multiplicando numerador y denominador por el mismo número (en este caso 2). |
|
|
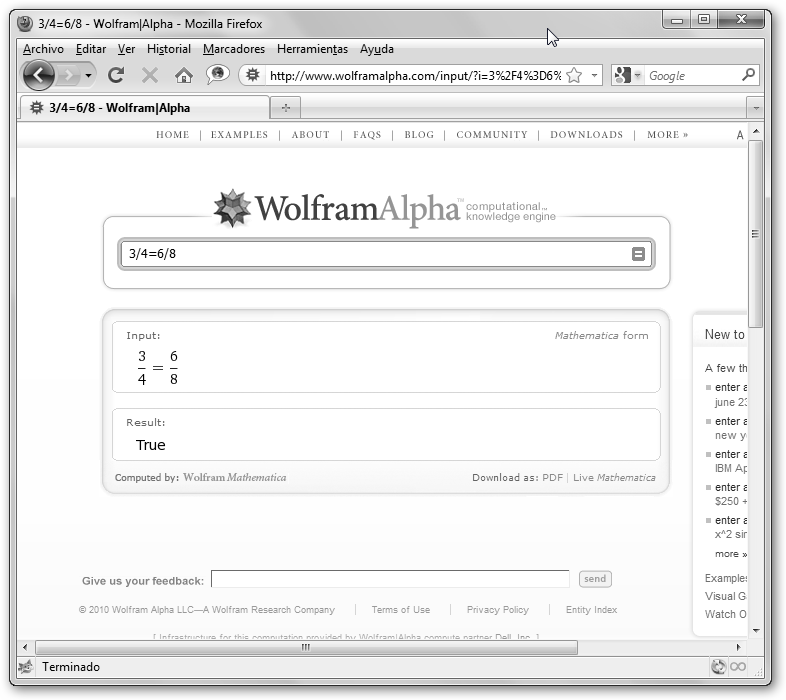
Con WolframAlpha podemos también comparar fracciones. Si escribimos 3/4=6/8 nos devuelve True, verdadero, es decir, se trata de dos fracciones equivalentes. |
|
|
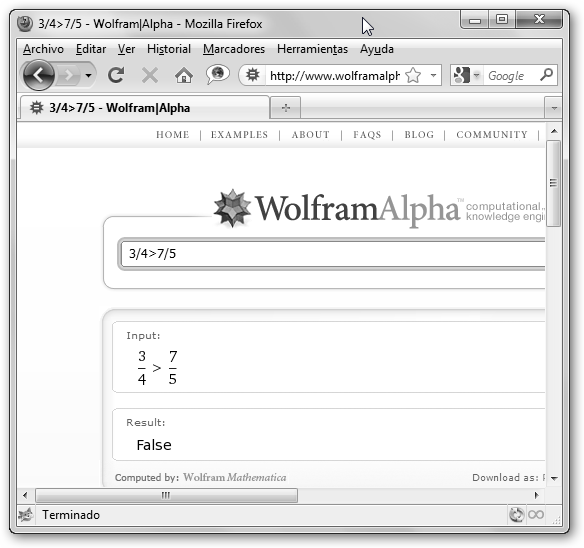
Si la consulta es 3/4>7/5 el resultado es False, falso pues 3/4<7/5. |
|
5.5. Aritmética de fracciones: ¡si empezamos con nombres raros me voy!
|
|
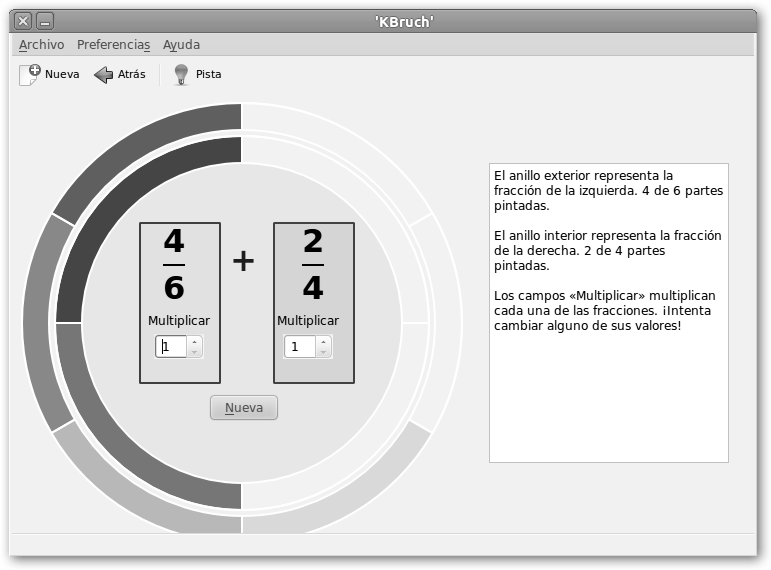
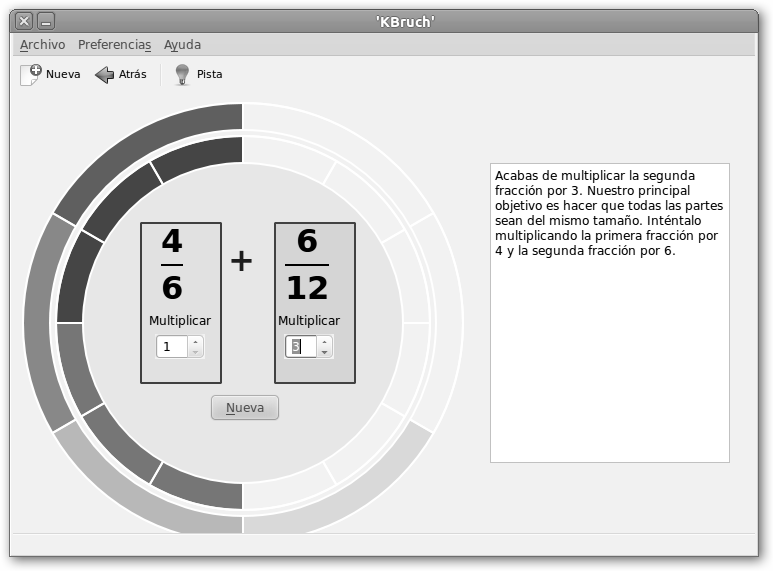
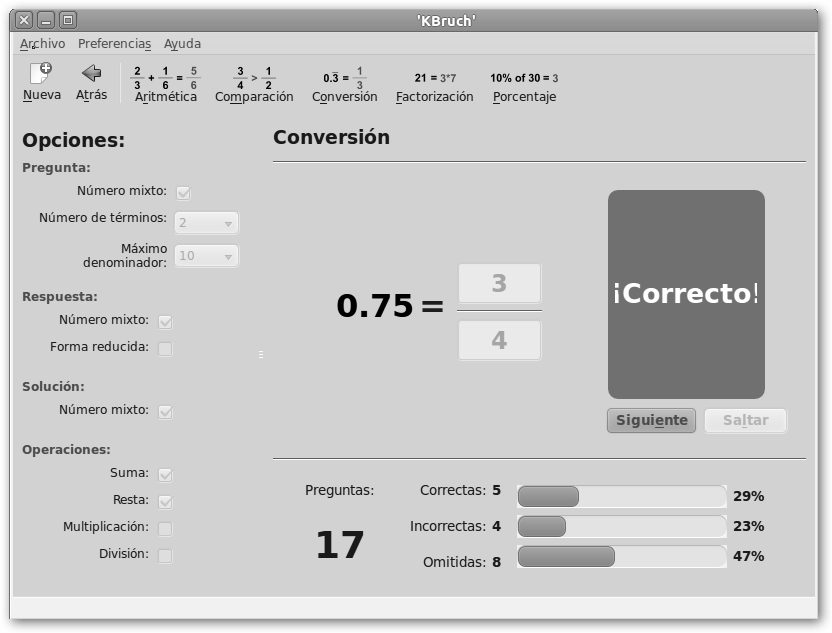
Si sigues desesperado, KBruch viene también en tu ayuda. Se trata de otra magnífica herramienta disponible para GNU/Linux para practicar el cálculo de fracciones y porcentajes. En Ubuntu basta instalar sudo apt-get install kbruch. Lánzalo desde Aplicaciones, Educación, KBruch y selecciona Aprendizaje. Observa que te propone la suma de dos fracciones, te muestra una ayuda en un cuadro a la derecha (que puede ocultarse haciendo clic en Pista) y una representación gráfica de las dos fracciones: anillos exterior (4/6, primer operando) e interior (2/4, segundo operando). |
||
|
Disponemos de dos cuadros de textos, etiquetados Multiplicar debajo de las fracciones, para obtener fracciones equivalentes de suerte que ambas tengan el mismo denominador y podamos sumarlas. |
El m.c.m(6,4)=m.c.m(2*3, 2*2)=22*3=12. Entonces, el denominador debe ser para ambas fracciones 12. Multiplica la segunda fracción por 3 y obtendrás 6/12. Observa que el anillo interior se ha dividido en doce porciones y seis están oscurecidas representando la nueva fracción. |
||
|
|
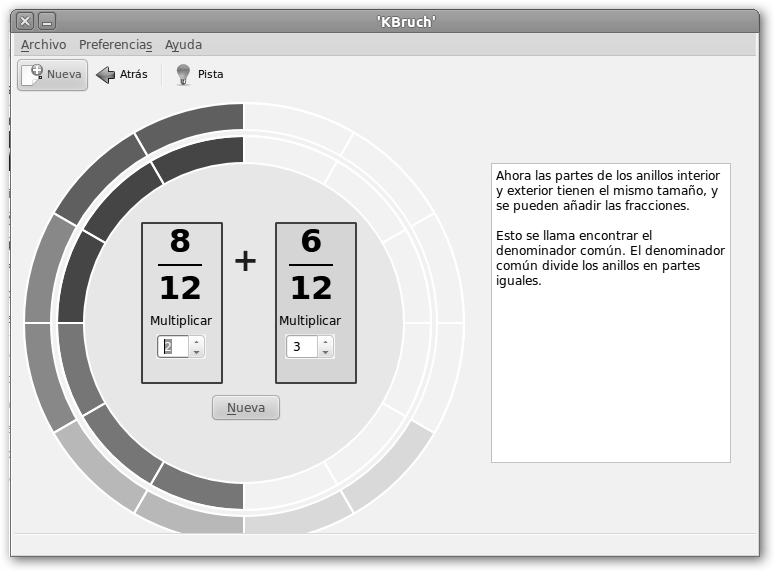
A continuación, multiplica la primera fracción por 2 y obtendrás 8/12. Ahora tenemos ambos anillos divididos en 12 partes. Para sumar las dos fracciones sumamos ambos numeradores (8+6=14) y dejamos el mismo denominador (12), es decir, 14/12=7/6. Haz clic en el botón Nueva para realizar otra actividad. ¡Podemos sumar porque si las tartas están divididas en el mismo número de partes, los trozos son iguales! |
Puedes utilizar también la siguiente fórmula:
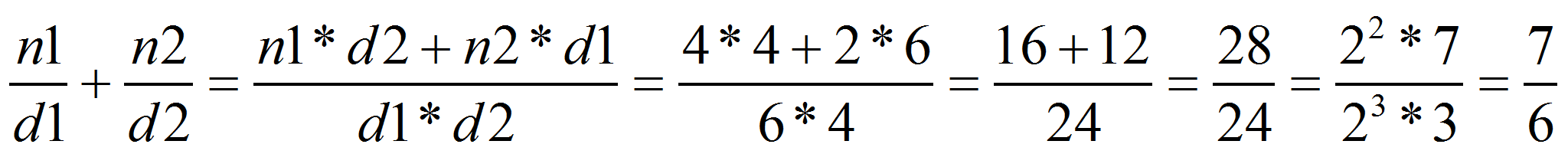
Dicho de otro modo, supongamos que nos quedan los restos de dos
tartas de cumpleaños. En una quedan 2 trozos y fue dividida
en seis y de la otra dejaron un trozo huérfano y se cortó
en cuatro. ¿Con los tres trozos restantes sería
justo darle a tres amigos (que se han incorporado muy tarde a la
fiesta) un trozo a cada uno? ¡Sí, pero a mí me dais el trozo de la tarta
que se ha dividido en cuatro partes! Pues va a ser que no,
porque los trozos de la primera tarta (1/6) son más
pequeños que los de la segunda (1/4).
¡Sí, pero a mí me dais el trozo de la tarta
que se ha dividido en cuatro partes! Pues va a ser que no,
porque los trozos de la primera tarta (1/6) son más
pequeños que los de la segunda (1/4).
|
|
|
|
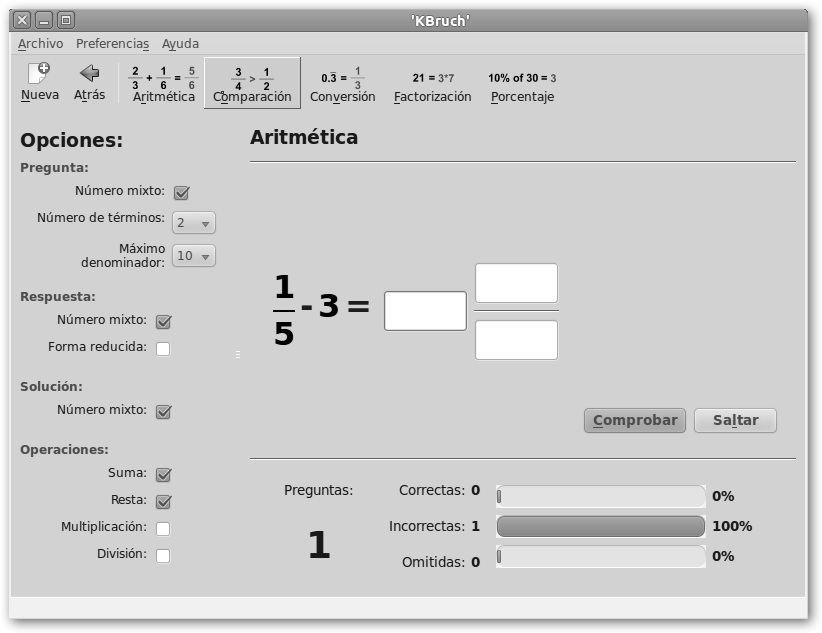
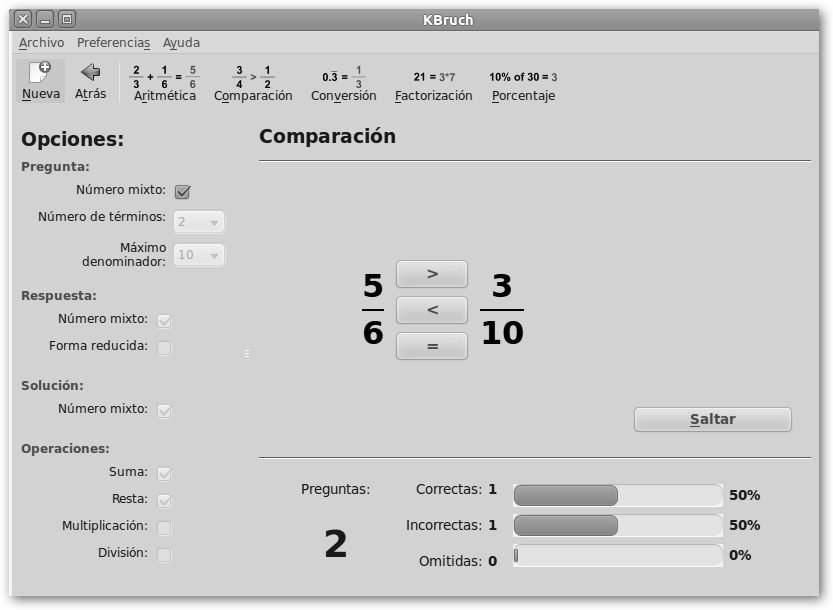
Si seleccionamos en KBruch la opción Estilo libre podemos trabajar: * Aritmética de fracciones: 2/3+1/6=5/6, 1/5-3=-14/5. * Comparación de fracciones: 5/6 >3/10, 3/4>1/2. * Factorización: 21=3*7, 250=2*53. * Porcentaje: 10% of 30=3, 25% de 1400=350. Con WolframAlpha también podemos trabajar simbólicamente con fracciones e incluso ver cómo lo resuelve internamente (Show steps). Observa tres ejemplos de suma, multiplicación y división de fracciones. |
|
|
Recuerda las siguientes fórmulas:
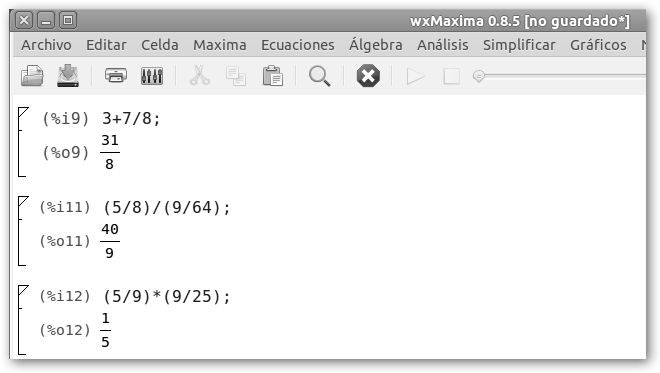
wxMaxima al igual que WolframAlpha también permite operar con fracciones tal como se ilustra en las siguientes figuras. |
Observa que simplifica el resultado, así
|
|
|
|
|
|
|
|
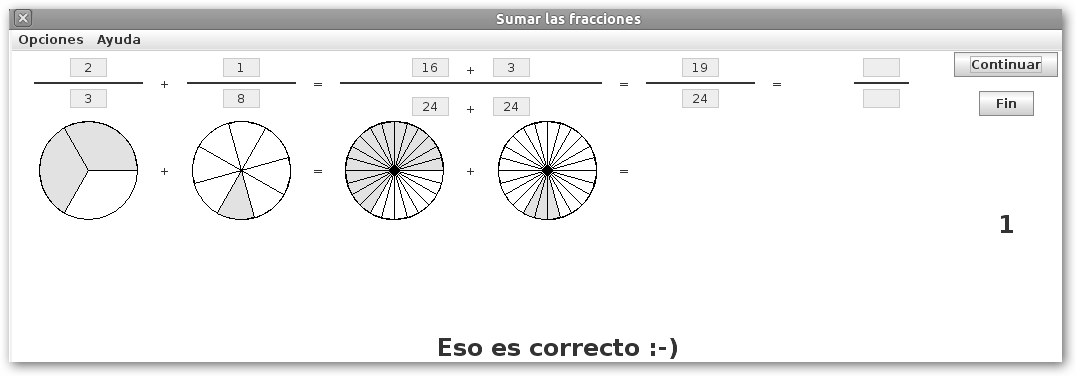
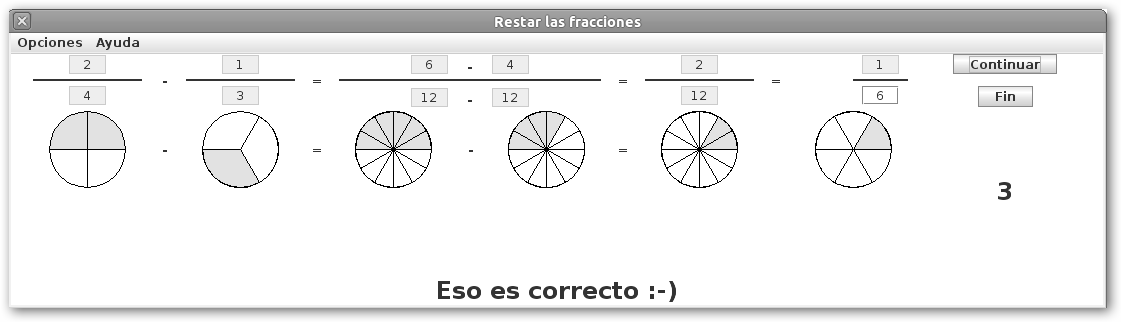
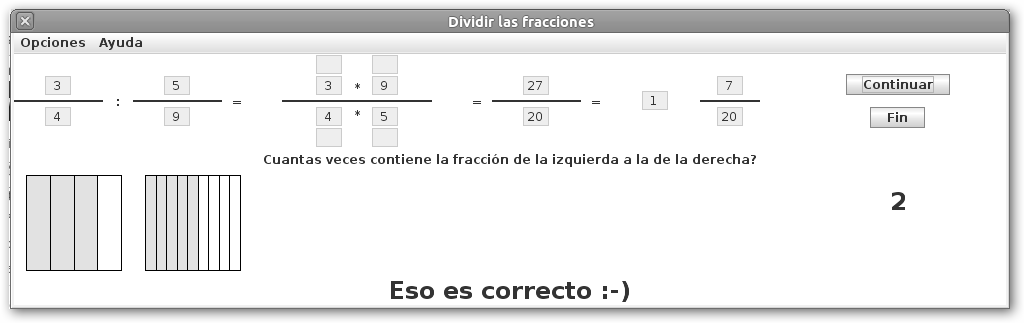
En JFractionLab dispones de las actividades: Sumar las fracciones, Restar las fracciones, Multiplicar las fracciones y División de una fracción por una fracción. Observa que te muestra siempre la representación gráfica de las fracciones para que sepas interpretar los cálculos. |
|
5.6. Fracciones impropias y mixtas
Ya sé que son raritas ,
pero ellas también tienen derecho a ser estudiadas. Existen
dos tipos de fracciones:
,
pero ellas también tienen derecho a ser estudiadas. Existen
dos tipos de fracciones:
* Propias: su numerador es menor que su denominador, por ejemplo: 3/5, 2/3, 1/2, etc.
* Impropias: su numerador es mayor que su denominador: 6/5, 4/3, 3/2, etc.
Una fracción mixta es la unión de un entero y una fracción propia, por ejemplo 2 ½, 3 ¼, etc. Así 3 ¼ significa tres tartas y un trozo de una tarta dividida en cuatro porciones. Toda fracción impropia se puede transformar en un número mixto. En JFractionLab tenemos dos actividades relativas a estas fracciones: Fracciones impropias y números mixtos.
Observa
que la fracción impropia 25/10 se transforma en el número
mixto 2![]() , es decir, dos tartas y cinco trozos de la tercera, una vez se ha
cortado esta última en diez partes. Fíjate que al dividir 25 (dividendo)
entre 10 (divisor) nos da como cociente 2 y resto 5. Luego 25/10 es igual a 2
, es decir, dos tartas y cinco trozos de la tercera, una vez se ha
cortado esta última en diez partes. Fíjate que al dividir 25 (dividendo)
entre 10 (divisor) nos da como cociente 2 y resto 5. Luego 25/10 es igual a 2
![]() , es decir, cociente
, es decir, cociente 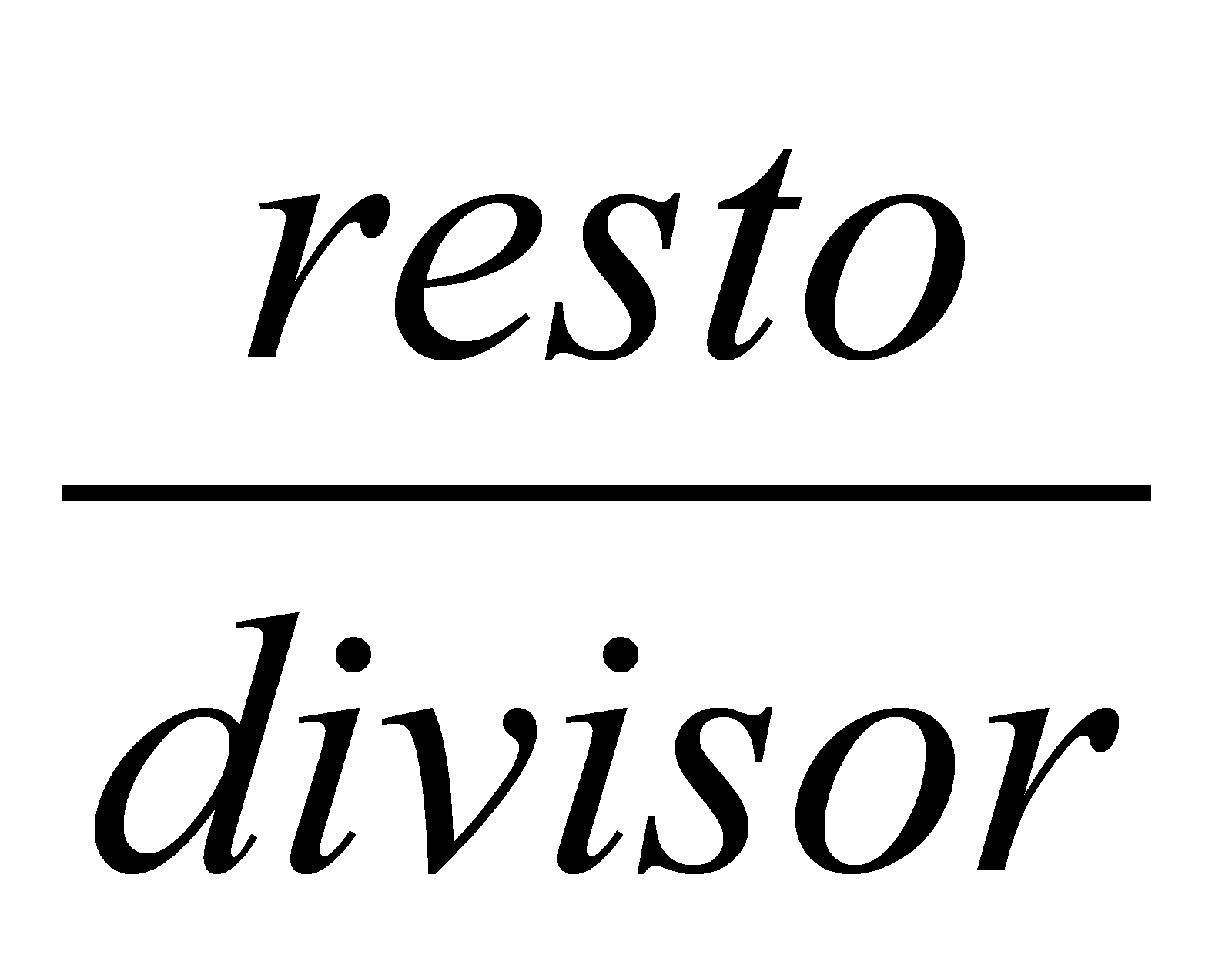 . De modo semejante, una fracción mixta podemos
pasarlo a una fracción impropia: 2
. De modo semejante, una fracción mixta podemos
pasarlo a una fracción impropia: 2![]() =n*
=n*
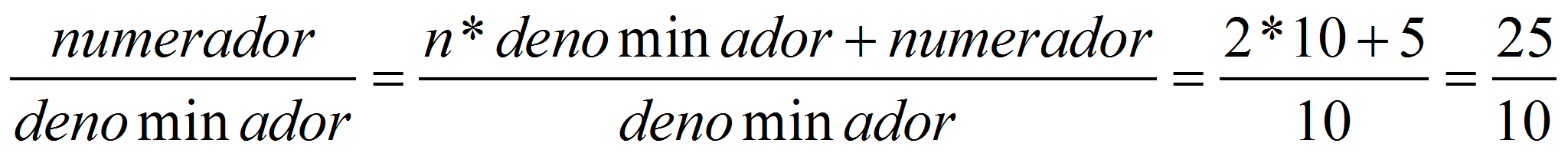 .
.
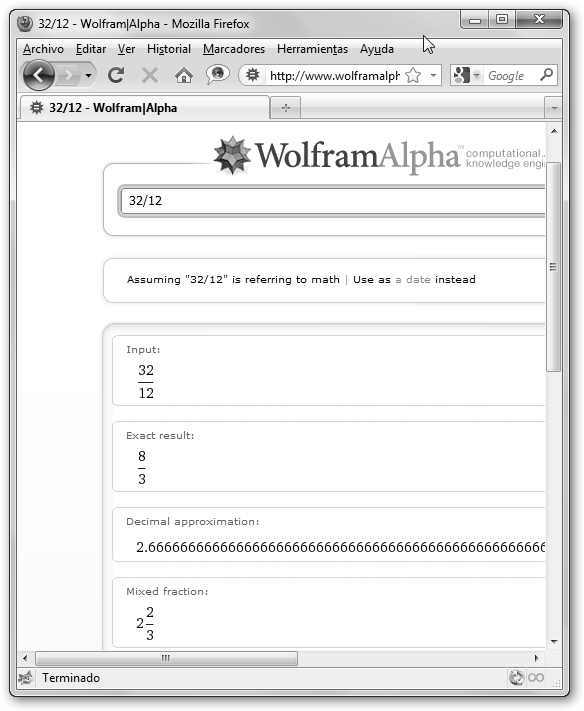
En WolframAlpha si introducimos una fracción impropia obtenemos la fracción simplificada o irreducible, así como, la fracción mixta equivalente y su valor decimal. ¡Bueno!, una aproximación, al tener infinitas cifras decimales el computador nos devuelve un resultado lo más cercano posible.
5.7. Representación de las fracciones en la recta real.
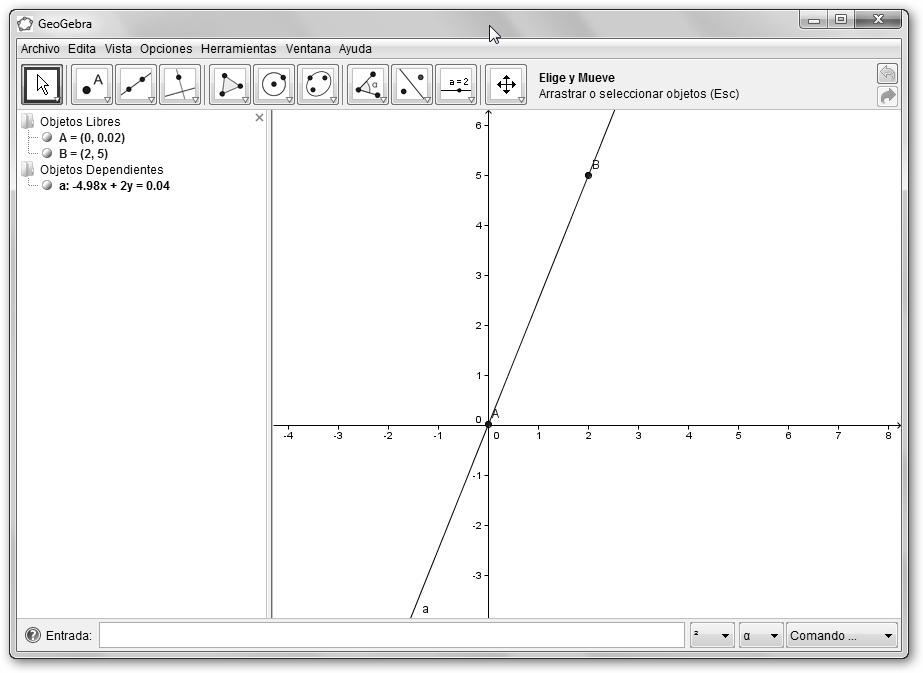
Vamos a representar 1/4 en la recta real y para ello utilizaremos GeoGebra.
|
|
|
|
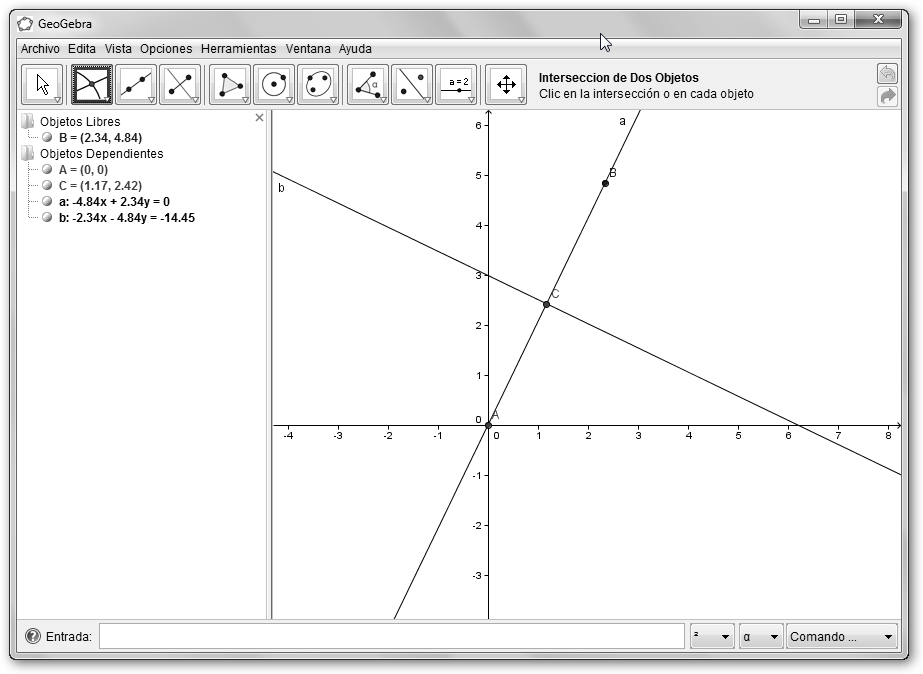
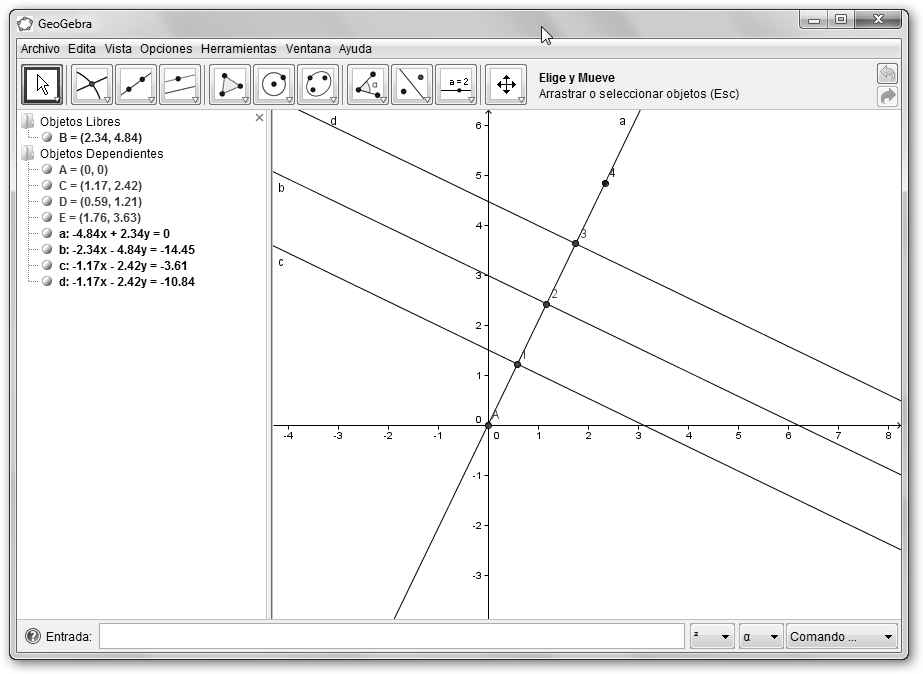
Con la herramienta Segmento entre dos puntos del menú Recta que pasa por Dos Puntos trazamos un segmento entre el punto (0,0) y cualquier otro punto arbitrario pero en el cuadrante superior derecho (recta a, segmento AB). |
Solicitamos la Mediatriz del menú Recta Perpendicular y pulsamos sobre la recta a (obtendremos la recta b, b=Mediatriz[a]). Calculamos la Intersección de Dos Objetos (del menú Nuevo Punto) de la mediatriz y el segmento original (punto C, C= Interseca[a, b]). |
|
|
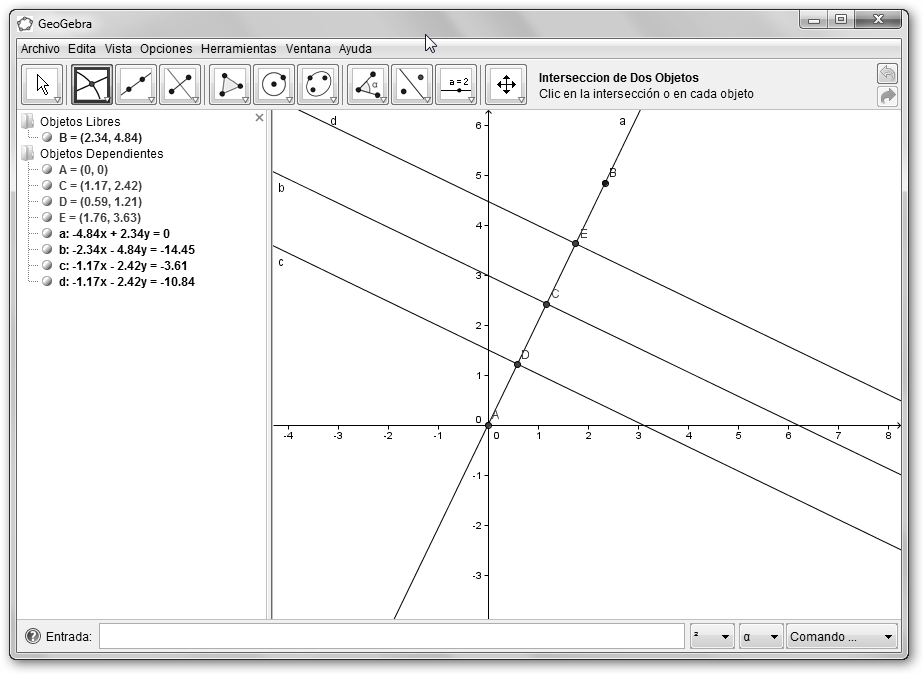
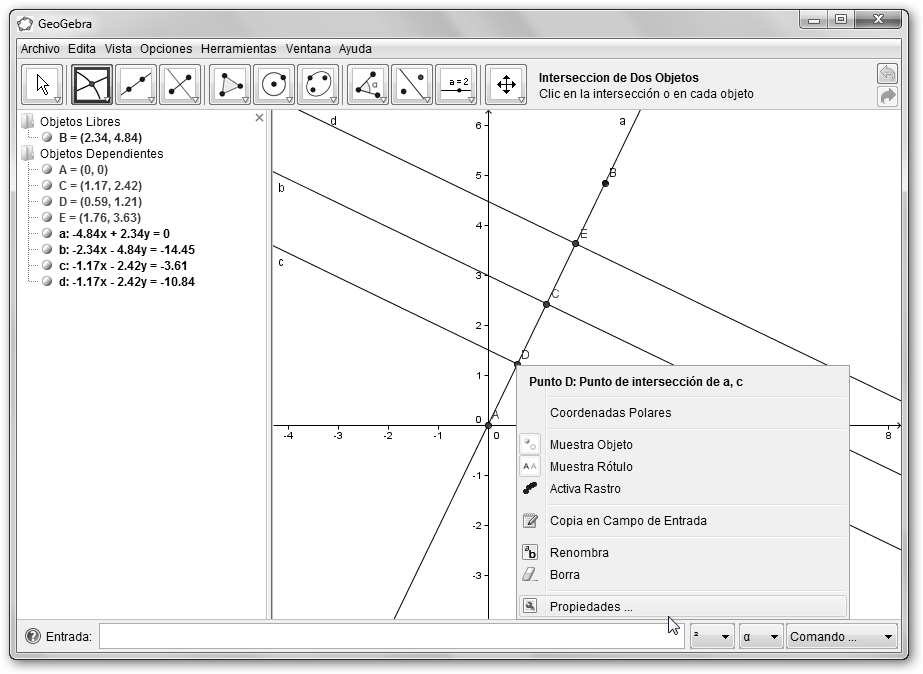
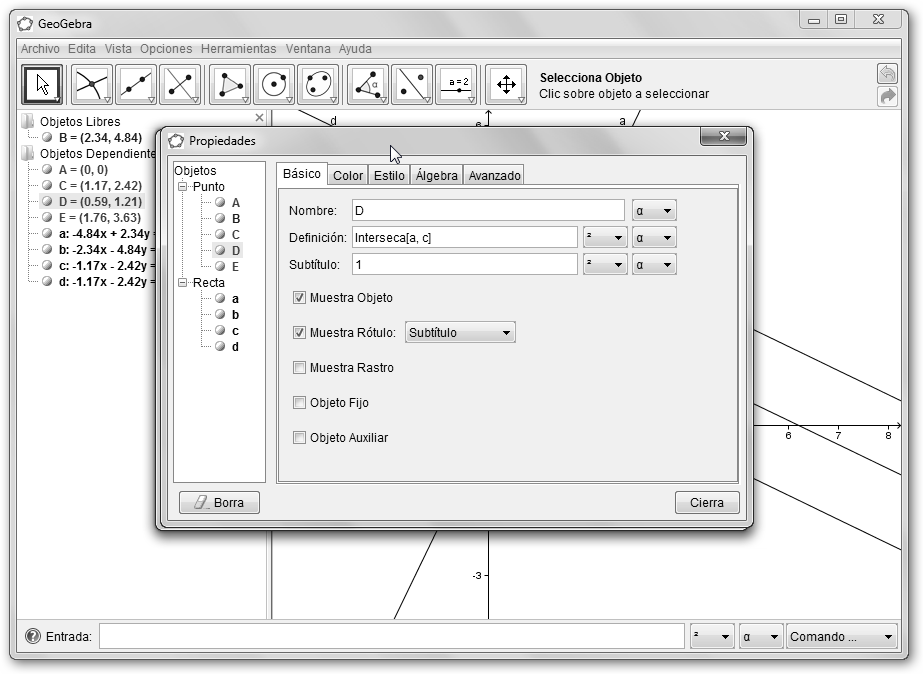
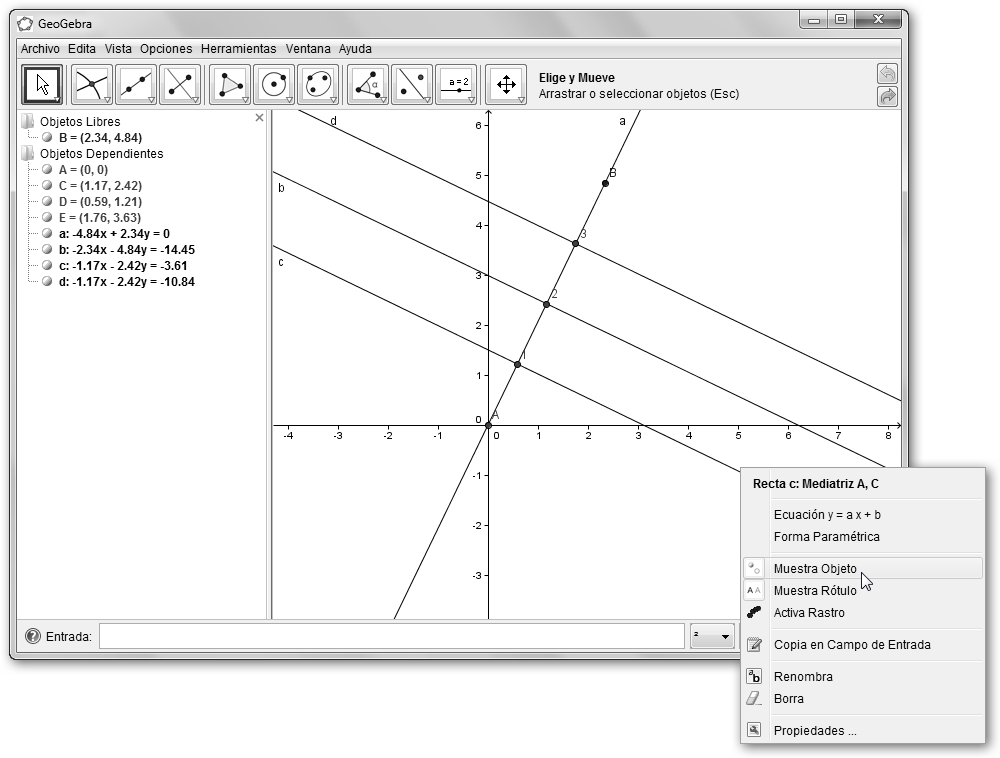
Volvemos a solicitar las mediatrices de los segmentos AC y CD desde la herramienta Mediatriz del menú Recta Perpendicular (rectas c y d). Obtenemos seguidamente los puntos D y E con la Intersección de Dos Objetos del menú Nuevo Punto con el segmento original AB y las rectas c y d respectivamente. A continuación, hacemos clic el punto D y seleccionamos en el menú contextual Propiedades. Escribe como Subtítulo, 1 y en Muestra Rótulo elige Subtítulo. |
|
|
|
|
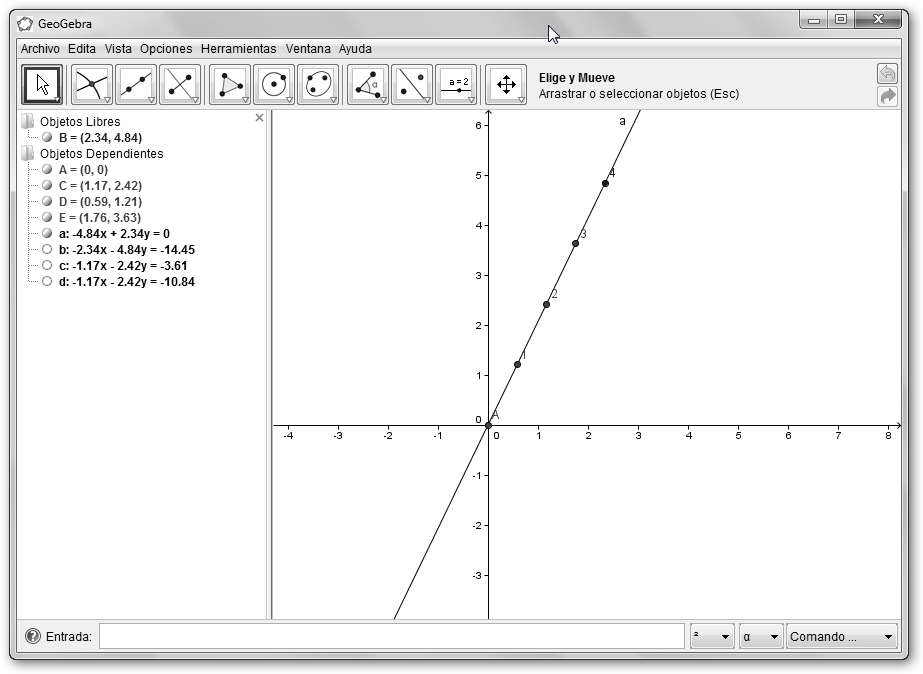
Haz lo mismo con el resto de puntos. Observa el resultado obtenido un segmento dividido en cuatro partes iguales y etiquetados con 1, 2, 3 y 4. |
Este paso no es realmente necesario pero mejora la comprensión del ejercicio. Vamos a ocultar las mediatrices que ya nos las necesitamos. Pulsa en las mediatrices y en el menú contextual selecciona Muestra Objeto. |
|
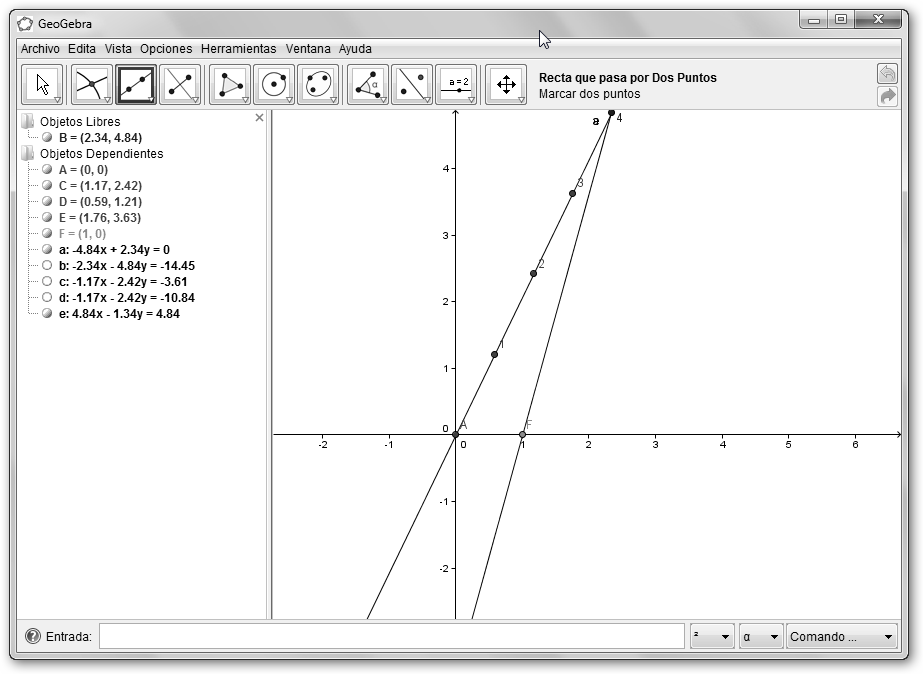
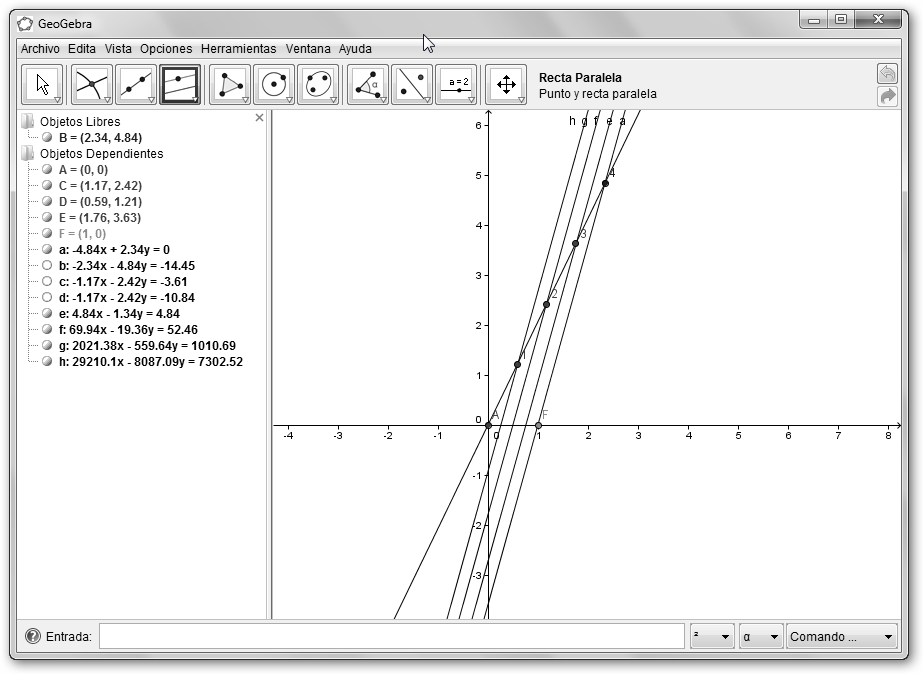
Traza rectas paralelas (Recta Paralela del menú Recta Perpendicular) al segmento recién creado entre (1,0) y el punto 4 con los puntos 3, 2 y 1 tal como se ilustra en la figura. |
Une el punto que hemos visualizado con 4 con (1,0) con la herramienta Segmento entre dos puntos del menú Recta que pasa por Dos Puntos.
|
|
Ojo al truquito: Con Ctrl+Alt o la tecla Windows y la bola del ratón podemos hacer Zoom. |
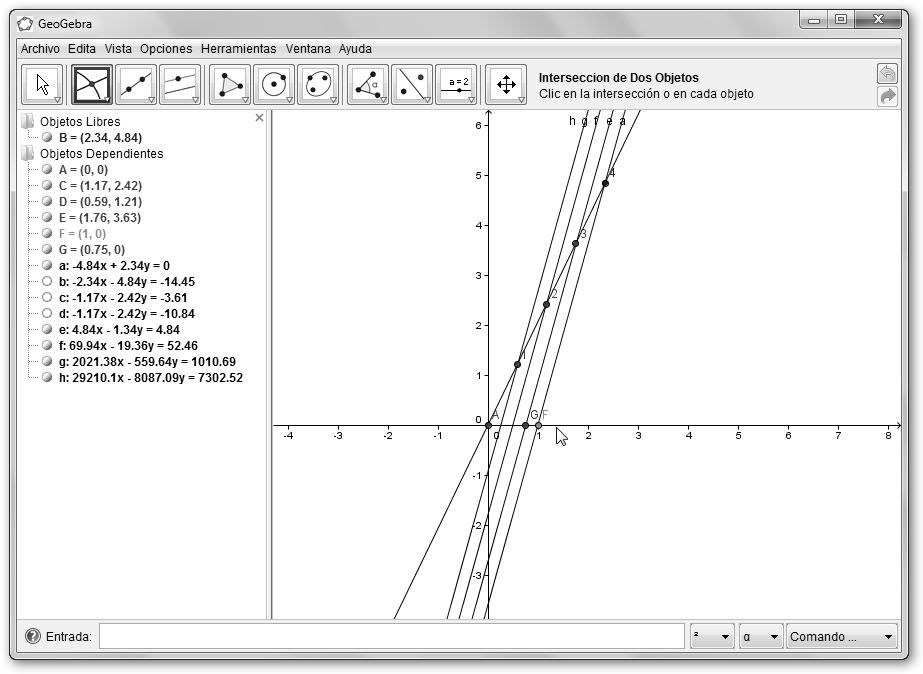
Ahora tenemos que dibujar los puntos intersección de las rectas recién creada con el eje de abscisas (Intersección de Dos Objetos del menú Nuevo Punto, observa el punto G). |
|
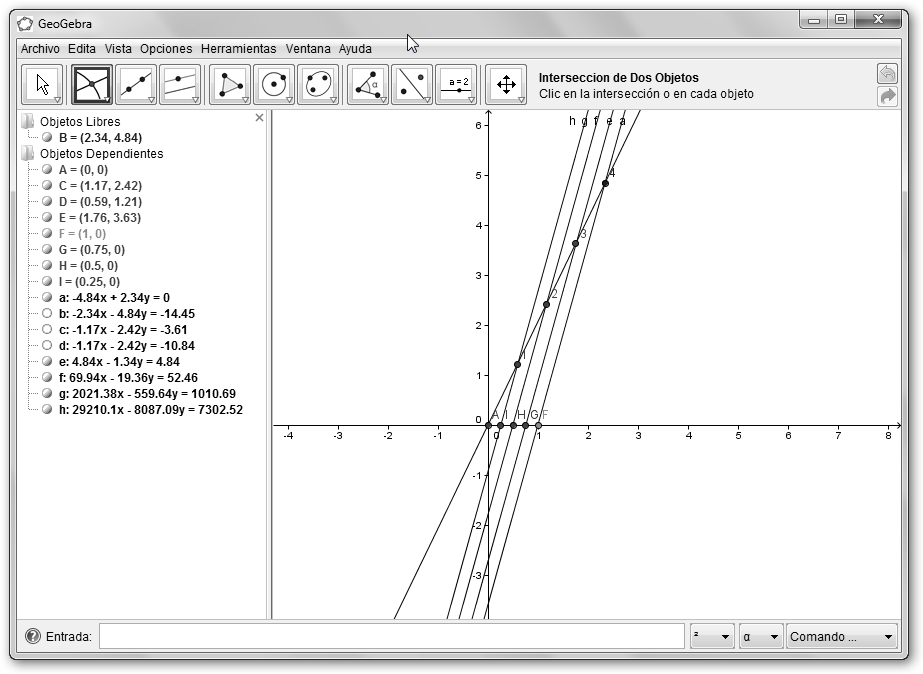
Haz lo mismo con el resto de paralelas. En la figura se obtienen los puntos I y H. |
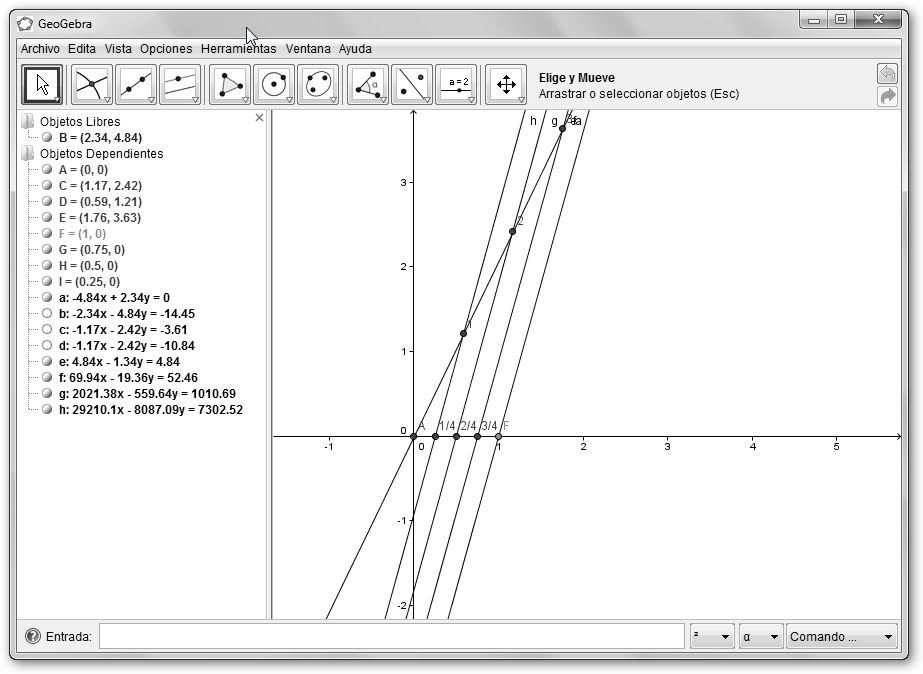
Para ayudar a interpretar los resultados hemos seleccionado en los puntos I, H, G en el menú contextual, la opción Propiedades. Se ha solicitado que se muestre el subtítulo y éste lo hemos definido como 1/4, 2/4 y 3/4. ¡Por fin! ¾. |
Observa
que hemos simplemente utilizado el Teorema de Thales. ¿Y si la
fracción es 4![]() ?
Se realizaría exactamente igual sólo que el segmento
inicial se deberá dibujar con el origen en (4,0) y deberemos
dividirlo en 7 partes iguales.
?
Se realizaría exactamente igual sólo que el segmento
inicial se deberá dibujar con el origen en (4,0) y deberemos
dividirlo en 7 partes iguales.
5.8. Números decimales.
Un número decimal (3,452) es aquel que tiene una parte entera (3), una coma (“,”) o un punto (“.”) y una parte decimal (452), por ejemplo: 3,452; 2,5; 4,789; etc.
Estos se clasifican en:
* Racionales: podemos expresarlo mediante una fracción, por ejemplo: 0,5=1/2, 0.75=3/4, 0.4=4/10, …
* Irracionales: los
que no podemos expresarlos como una fracción: Pi, e,
![]() ,
…
,
…
5.8.1. Conversión de números decimales a fracciones.
|
|
|
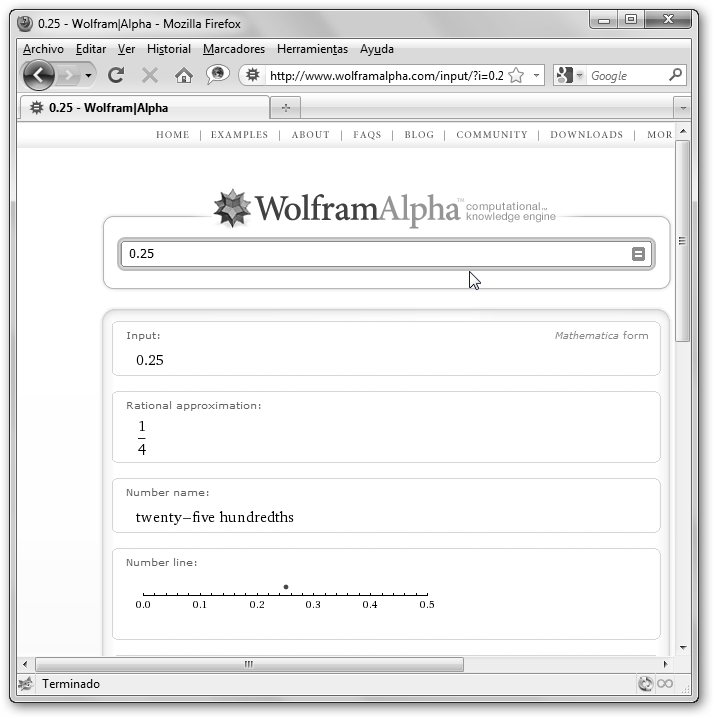
Hemos realizado varios ejercicios de pasar de números decimales a fracciones de dos formas:
* KBruch: Seleccionando en Estilo libre, la actividad Conversión.
* WolframAlpha: escribe simplemente el número decimal y observa la sección Rational approximation, aproximación racional.
Si el número decimal es exacto (0,75), es decir, tiene un número finito de decimales (en el ejemplo 2), la conversión es sencilla. Solo escribimos la parte decimal como numerador y como denominador la unidad seguida de tantos ceros como números decimales tenga, en este caso 2, sería por tanto 75/100 que al simplificar es 3/4.
5.8.2. Conversión de fracciones a números decimales.
|
Para convertir una fracción a número decimal, solo precisas dividir el numerador por el denominador tal como se ilustra en la figura.
En el ejemplo 9,4 es la expresión decimal de la fracción 47/5 que se llama fracción generatriz. |
Para comprobarlo, usa una calculadora, por ejemplo, navega por Inicio, Todos los programas, Accesorios, Calculadora. Pulsa: “47”, “/”, “5” y “=”, obtendrás 9,4. |
Sin embargo, no siempre sale tan bonito![]() .
Tenemos varias posibilidades:
.
Tenemos varias posibilidades:
1. Decimal exacto: La parte decimal tiene un número finito (limitado de números), por ejemplo: 47/5=9,4; 3/4=0.75; 5/8=0.625; etc.
2. Decimal periódico puro:
La parte decimal se repite infinitamente y la llamamos periodo: 1/3=0.
![]() ; 5/3=1.
; 5/3=1.![]() .
.
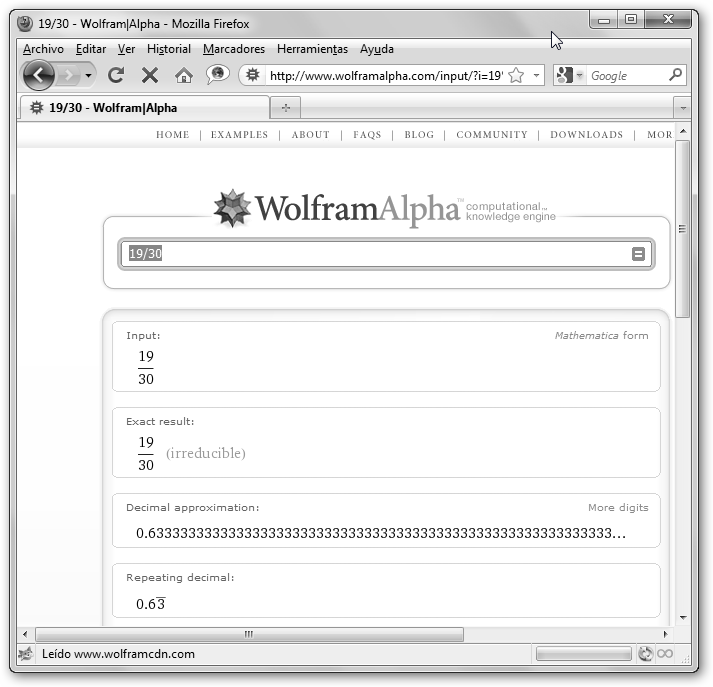
3. Decimal periódico mixta:
La parte decimal (.6![]() )
tiene una parte no periódica (6) y otra periódica (3):
19/30=0.6
)
tiene una parte no periódica (6) y otra periódica (3):
19/30=0.6![]() ; 11/15=0.7
; 11/15=0.7![]() .
.
4. Decimales ni exactos ni
periódicos: Aquellos que tienen infinitas cifras decimales y además
no se repiten: pi,![]() .
.
|
|
Observa que siempre podemos indicarle que nos muestre más cifras decimales haciendo clic en More digits. |
|
|
Con nuestro amigo WolframAlpha Mostramos los diferentes tipos. ¡Esto es
dogma! |
5.8.3 Tu primero, tu segundo,…
|
Ordenar los números decimales es terroríficamente
1. Es más pequeño el que tenga la menor parte entera. 2. Si ambos tienen la misma parte entera (3), entonces nos fijaremos en el primer dígito de la parte decimal. El que lo tenga menor (5<6) será el más pequeño. 3. ¿3,52 < 3,567? Si esto no funciona, buscaremos el segundo dígito decimal, en este caso 2<6. Luego 3,52 < 3,567. Y así, sucesivamente… |
Observa que siempre podemos preguntar a WolframAlpha o Maxima con la orden is.
|
5.8.4. Operando con números decimales.
Cualquier calculadora te servirá para comprobar que cuando realices operaciones aritméticas con números decimales tus resultados son correctos. En la figura se ilustra SpeedCrunch (www.speedcrunch.org), pero puedes utilizar WolframAlpha, Google, Microsoft Mathematics, Qalculate!, etc.
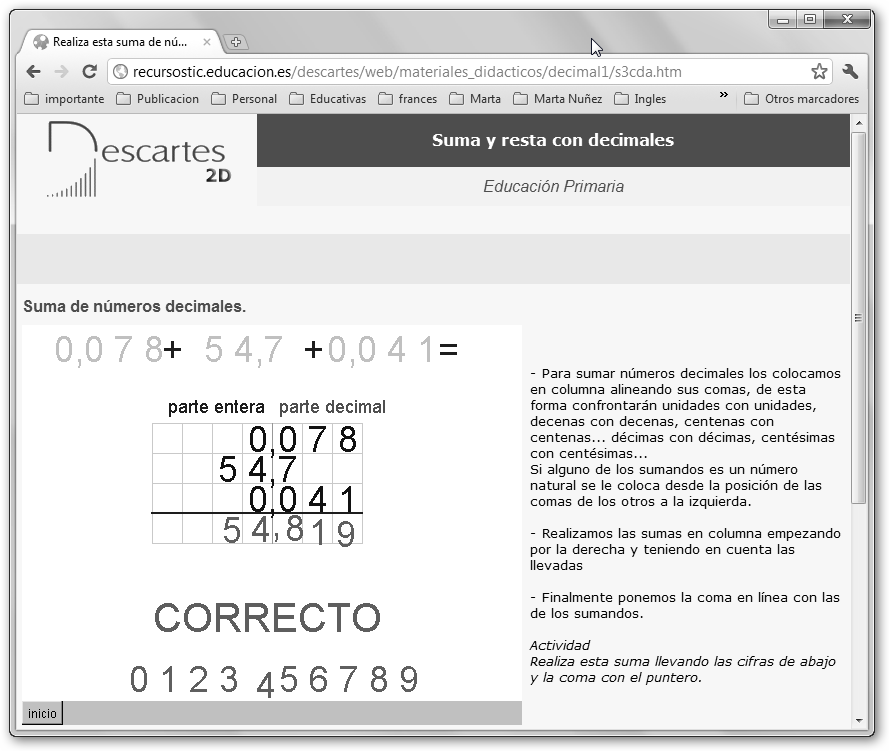
Si quieres una explicación y una actividad más guiada puedes recurrir a Descartes: navega por recursostic.educacion.es/descartes/web/, U. Didácticas y selecciona Los números decimales: Suma y Resta y Los números decimales: Multiplicación y División. En la figura se explica cómo sumar tres números decimales: coloca primero los números alineados por la coma y en segundo lugar realiza las sumas empezando por la derecha y teniendo en cuenta las llevadas.
5.9. Porcentajes
Un porcentaje, por ejemplo un 40% (se lee como cuarenta por ciento), es una forma de expresar una cantidad, “un número como una fracción de cien” (extraído de la Wikipedia), en nuestro caso significaría un 40 de cada 100. Si decimos que el 40% de los españoles cuestionan la Constitución significa que de cada 100 españoles, 40 cuestionan la Carta Magna.
|
Un porcentaje se puede representar como una fracción ( Si queremos en WolframAlpha o Google solicitar el 75% de 1100 o el 40% de 1100 sólo tienes que trasladarlo al inglés: 75% of 1100, 40% of 125.
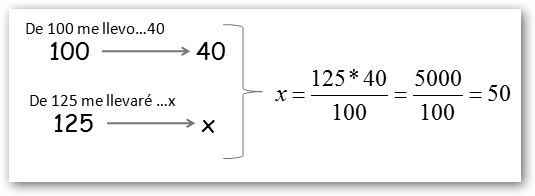
¿Cómo se calcula? Es una sencilla regla de tres:
|
|
|
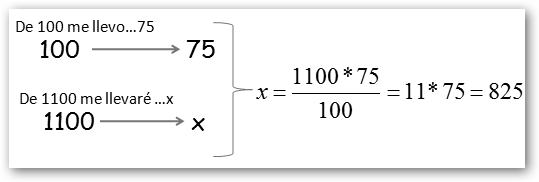
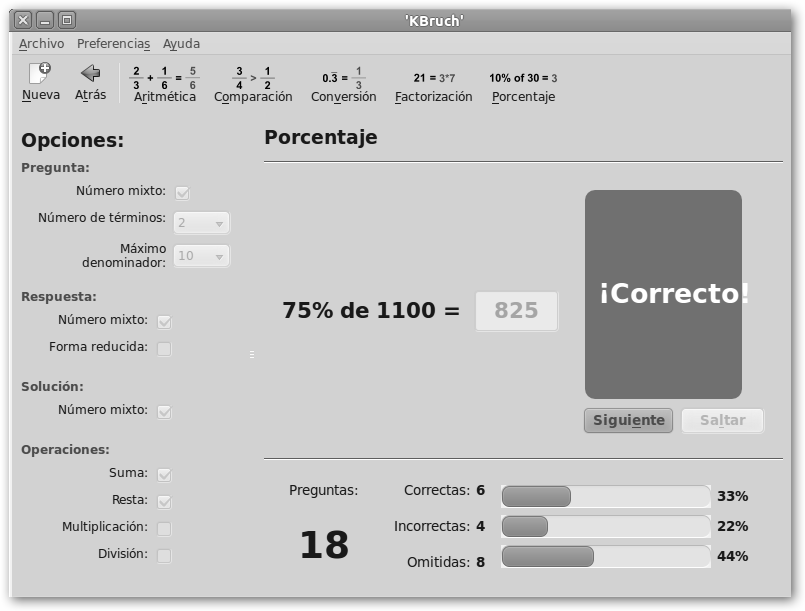
También puedes trabajar con KBruch, en Estilo Libre la actividad Porcentaje. Observa que en este ejemplo sería:
En vez de multiplicar 1100*75, he sido más astuto y he dividido numerador y denominador por 100. ¡Lo estaba pidiendo a gritos! |
|
5.10. Números insensatos…bueno, irracionales.
Los números enteros
(Z) son los números naturales N (1, 2, 3, 4,…los que necesitamos para
contar  ), el incomprendido cero
), el incomprendido cero
 y los números enteros negativos (-1, -2, -3,
-4,…). Acabamos de estudiar los números racionales (Q), es decir, todos
los números que pueden representarse como el cociente de dos enteros. Sin
embargo, nuestro cero no puede ser el denominador. Observa además que todos los
números enteros son racionales (Z
y los números enteros negativos (-1, -2, -3,
-4,…). Acabamos de estudiar los números racionales (Q), es decir, todos
los números que pueden representarse como el cociente de dos enteros. Sin
embargo, nuestro cero no puede ser el denominador. Observa además que todos los
números enteros son racionales (Z ![]() Q):
Q):
* 0 es 0/1, 0/2,…
* Naturales: 1=1/1=2/2=…, 2=2/1, 3=3/1, etc.
* Enteros negativos: -1=-1/1; -2=-2/1; -3=-3/1, etc.
Sin embargo, en la recta real quedan “huecos” y estos son
los números irracionales. Veamos lo que queremos decir en un
ejemplo. Si tenemos un triángulo equilátero con dos
catetos de lado 1, por el teorema de Pitágoras su hipotenusa
vendría dado por la siguiente fórmula: h2=c12+c22,
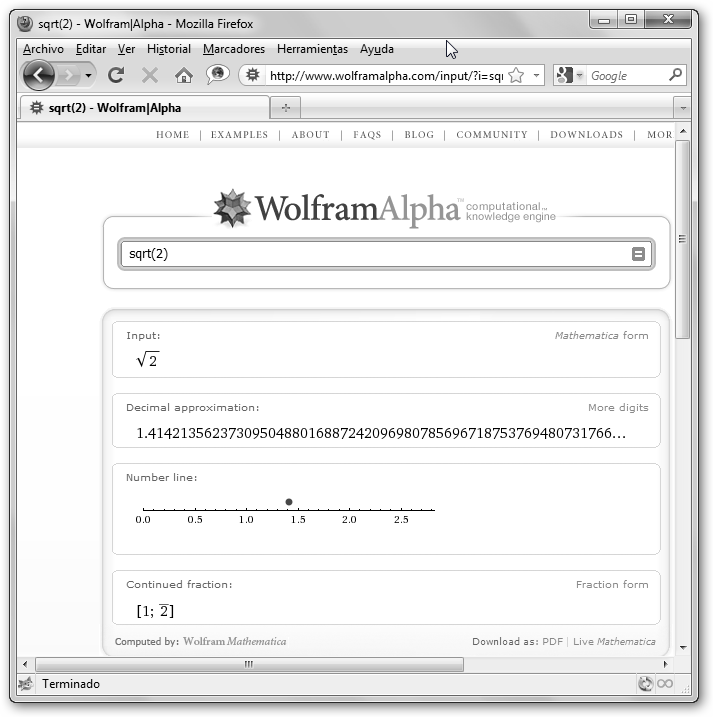
por lo que h2=2, en otras palabras h=![]() que es un número irracional y, por tanto, no se puede
representar como una fracción.
que es un número irracional y, por tanto, no se puede
representar como una fracción.![]()
|
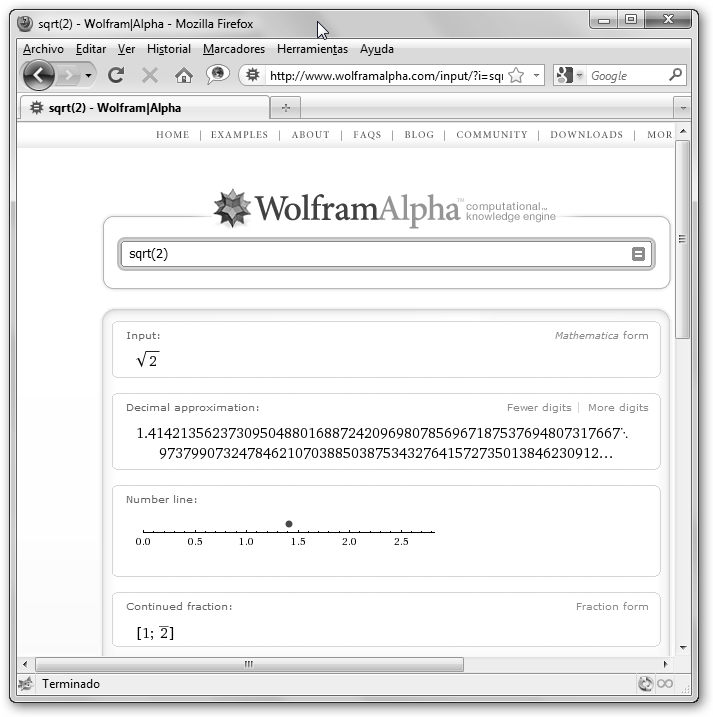
Haciendo clic en More digits puedes observar cómo se incrementa la cantidad de decimales. |
|
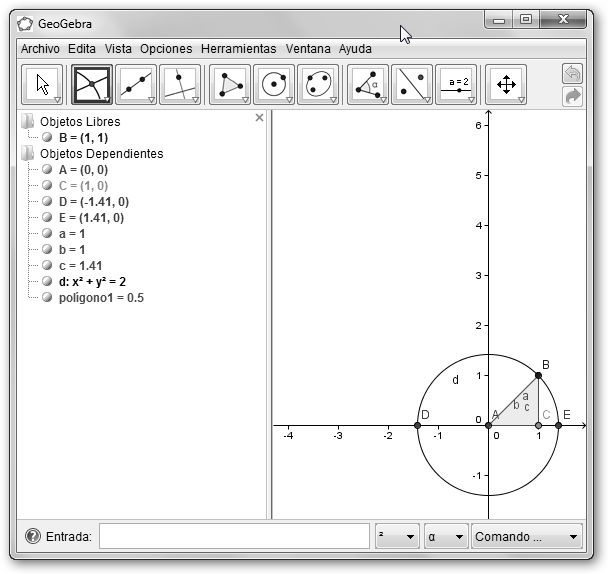
Se
ilustra en la izquierda el número irracional
![]() en WolframAlpha. En la derecha hemos dibujado un triángulo que
pase por los puntos (0, 0), (1, 1) y (1, 0) con la herramienta
Polígono (o escribe en la entrada: Polygon[(0,0),
(1,1), (1,0)]). Luego dibuja un círculo con centro el
punto (0,0) que pase por B (1, 1). Utiliza la herramienta
Circunferencia dado su Centro y uno de sus Puntos o escribe
Circunferencia[(0,0), (1,1)]. Finalmente, calcula la
intersección de dicha circunferencia con el eje de abscisas
(horizontal) para obtener E. Esto lo puedes realizar desde el menú
Nuevo Punto la opción Intersección de dos
Objetos. ¡Este punto de la recta real es un hueco que no se
cubre con los números racionales!
en WolframAlpha. En la derecha hemos dibujado un triángulo que
pase por los puntos (0, 0), (1, 1) y (1, 0) con la herramienta
Polígono (o escribe en la entrada: Polygon[(0,0),
(1,1), (1,0)]). Luego dibuja un círculo con centro el
punto (0,0) que pase por B (1, 1). Utiliza la herramienta
Circunferencia dado su Centro y uno de sus Puntos o escribe
Circunferencia[(0,0), (1,1)]. Finalmente, calcula la
intersección de dicha circunferencia con el eje de abscisas
(horizontal) para obtener E. Esto lo puedes realizar desde el menú
Nuevo Punto la opción Intersección de dos
Objetos. ¡Este punto de la recta real es un hueco que no se
cubre con los números racionales!
En otras palabras, da un paso ,
gira 90º y da otro paso idéntico en longitud, la
distancia a donde empezaste no podemos medirlo, sólo
aproximarnos.
,
gira 90º y da otro paso idéntico en longitud, la
distancia a donde empezaste no podemos medirlo, sólo
aproximarnos.
5.11. Conversión entre diferentes unidades de medida.
Vamos a convertir entre diferentes unidades de medida. Esto nos toca hacerlo por culpa de los ingleses que son muy suyos: pulgadas, pies, pinta, acre, la libra, conducir por la izquierda, ¡Gibraltar español! Hombre…, que ya está bien con tanto Sir Francis Drake que sólo fue un pirata. Podemos hacerlo con multitud de herramientas, con cada una de ellas utilizaremos distintas categorías: temperatura, tiempo, longitud, masa, área, etc.
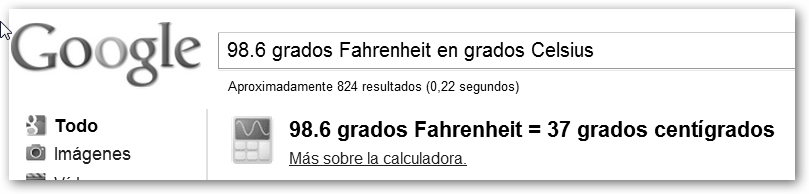
|
En Google mostramos como convertir entre unidades de temperatura y tiempo. |
|
|
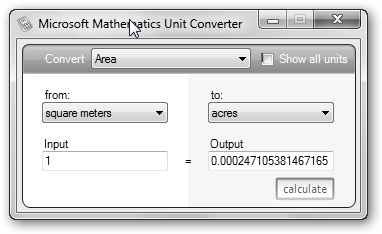
Abre Microsoft Mathematics desde Inicio, Todos los programas, Microsoft Mathematics, Microsoft Mathematics y selecciona Unit Converter, conversor de unidades. |
Elige la categoría a convertir, por ejemplo Area y selecciona que deseas pasar de (from) una unidad (square meters, metros cuadrados) a (to) otra (acres, medida anglosajona). Indica la cantidad en el cuadro de texto Input y pulsa calculate. |
|
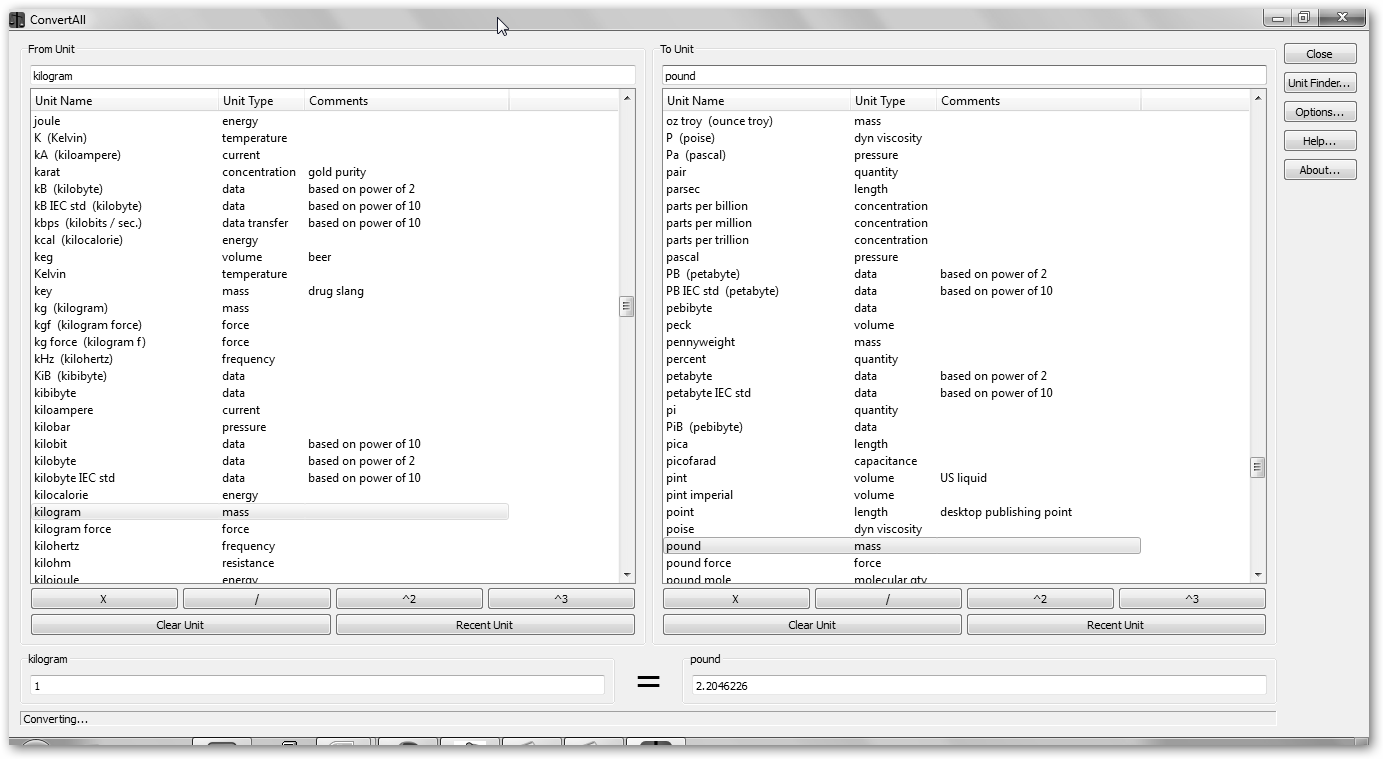
También podemos utilizar Convert All en convertall.bellz.org, disponible para Windows y Linux. En Ubuntu instala el paquete convertall (sudo apt-get install convertall). Selecciona en From Unit la unidad a convertir (en el ejemplo, kilogramo) y en To Unit, la destino (en el ejemplo pound, libras). Observa que si tecleas 1 en el cuadro de texto kilogram obtendrás que es igual a 2.2046226 pound (libras). |
|
|
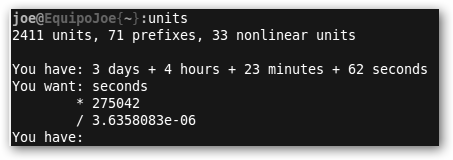
Escribe en You have, lo que tenemos: 3 días, 4 horas, 23 minutos y 62 segundos y lo queremos en segundos (You want: seconds). Devuelve 275042 segundos (*275042), /275042 es la conversión a la inversa. |
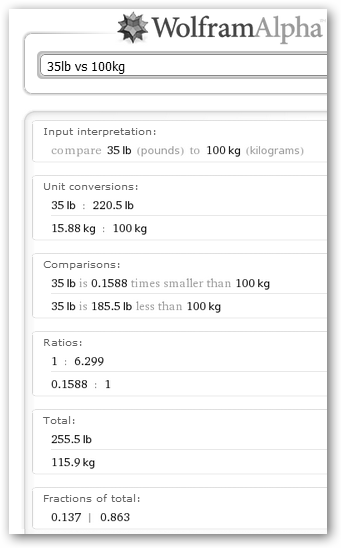
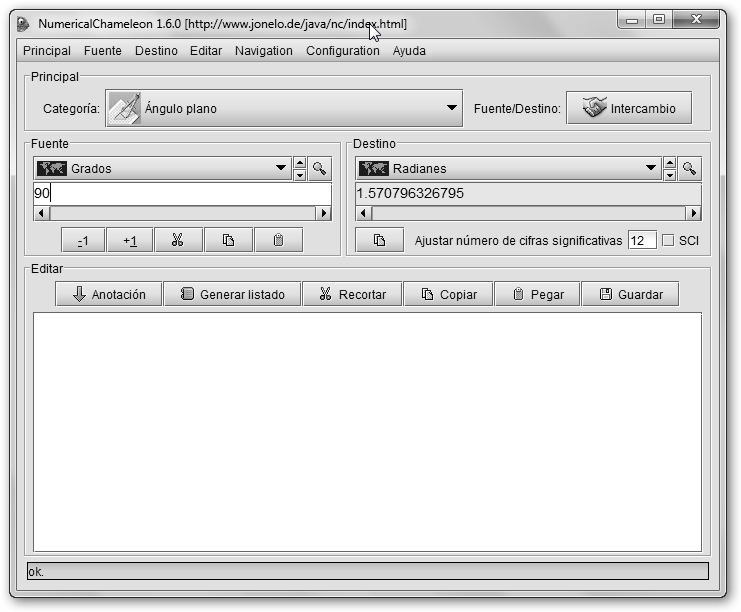
Otras posibilidades son: * Wolfram: 35lb vs 100kg, compara unidades; 10 yards + 7 kilometers, las suma. * Numerical Chamaleon en www.jonelo.de/java/nc. Se muestra como convertir 90 grados a radianes: Pi/2≈1.57. * En Linux tenemos para la consola units (sudo apt-get install units).
|
5.12. Proporciones y la Regla de tres.
Mira estos ejemplos: si un kilo de limones me cuesta 2 euros, si compro tres kilos me costará el triple, 6 euros; si gasto en gasolina 1 litro en recorrer 25 kilómetros, gastaré 2 litros en recorrer 50; si necesito un obrero para pintar cuatro casas en un mes, para pintar una urbanización con veinte casas en el mismo tiempo necesitaré cinco curritos. Se habla de proporcionalidad directa entre dos magnitudes cuando al variar una, por ejemplo, hago que sea el doble, la mitad, el triple o el cuádruple, la otra varía de la misma forma (doble, la mitad, el triple o el cuádruple). Otra manera de expresarlo sería que las relaciones entre el peso de los limones y su precio o entre la gasolina y los kilómetros recorridos pueden reflejarse en una proporción. Fíjate:
* Peso de los limones y su precio:
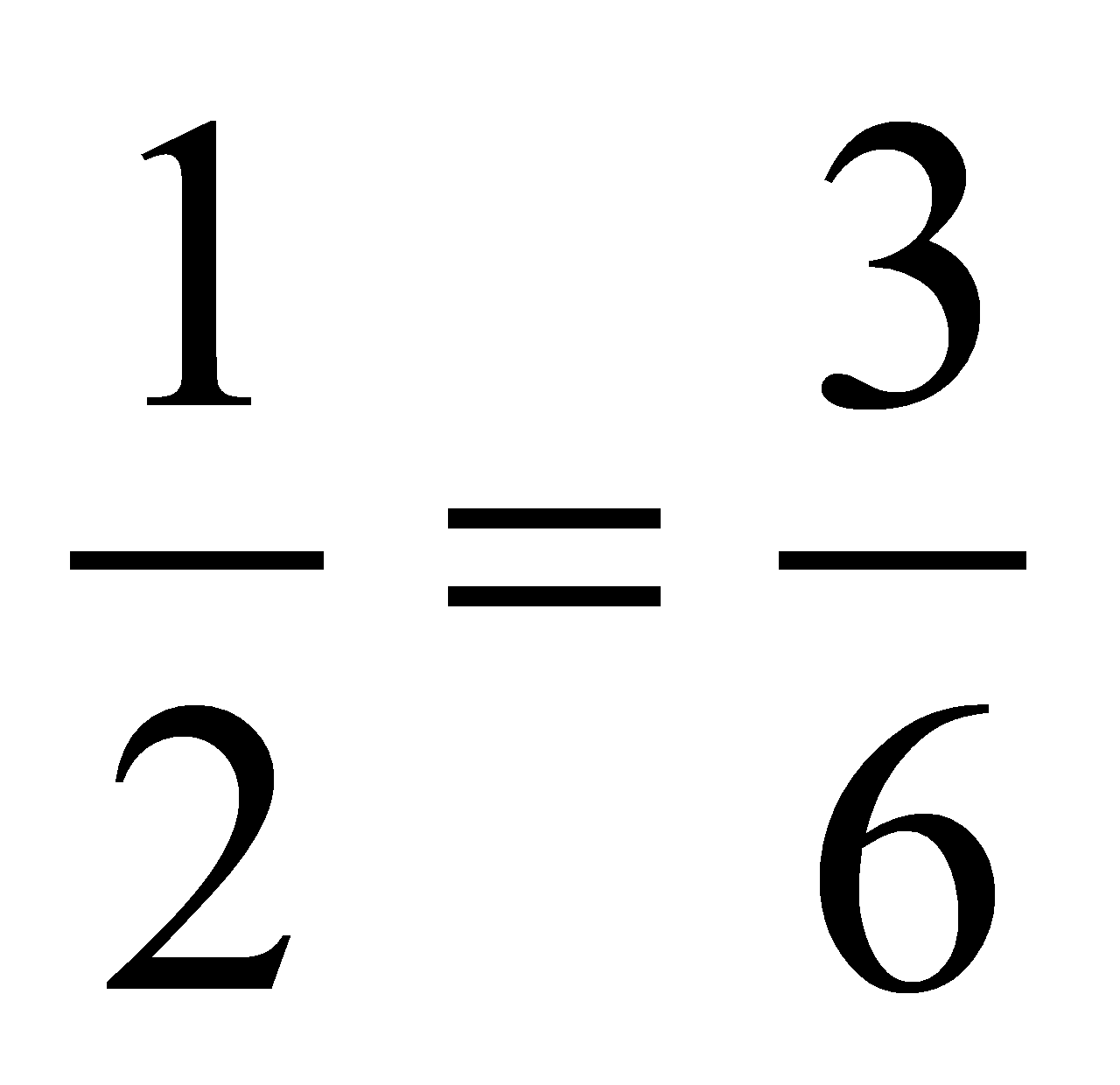 =0.5 que es la constante de proporcionalidad.
=0.5 que es la constante de proporcionalidad.
* Gasolina y kilómetros
recorridos: 
* Casas y obreros:
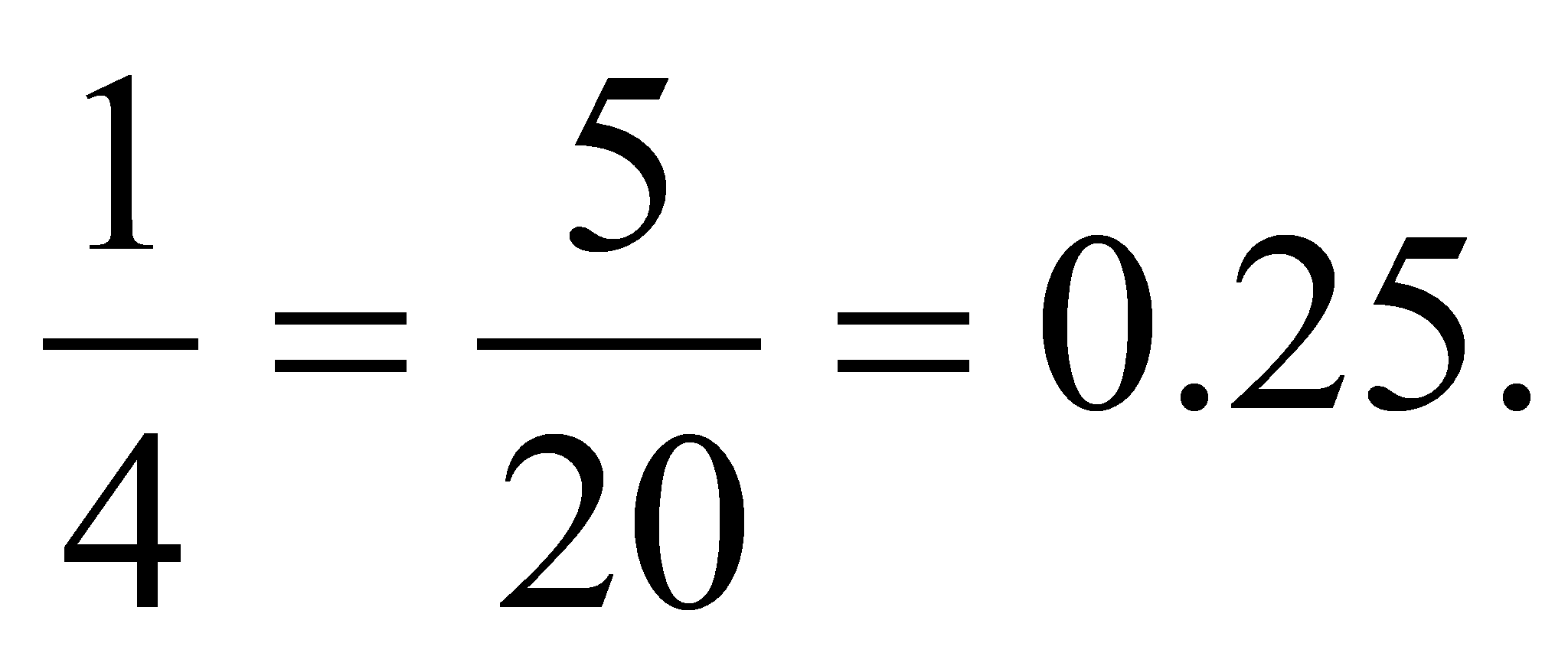
|
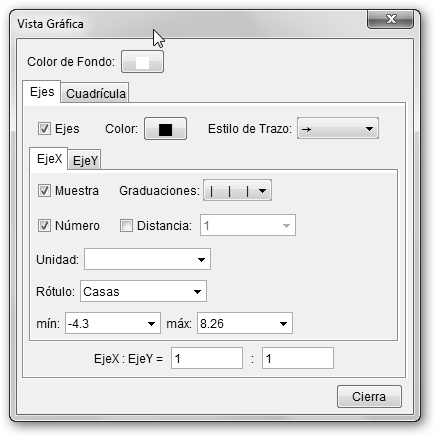
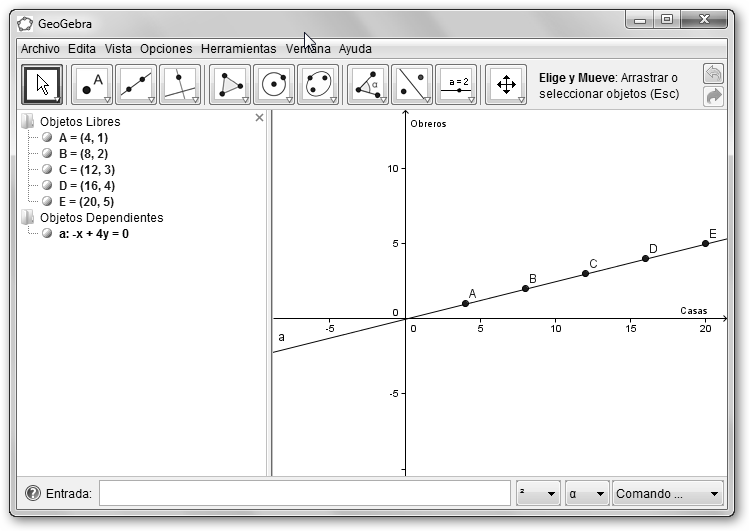
Veámoslo gráficamente: 1. Arranca GeoGebra: Inicio, Todos los programas, GeoGebra WebStart, GeoGebra WebStart. 2. Seleccionamos uno de los ejes y en el menú contextual (con el botón derecho del ratón) selecciona Vista Gráfica. Cambia el Rótulo tanto del Eje X (Casas), como del Eje Y (Obreros). |
|
|
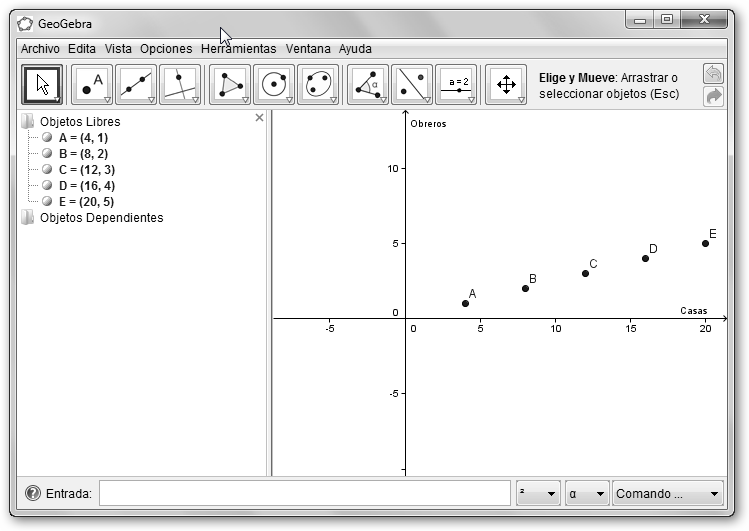
3. Crea los siguientes puntos desde el menú Nuevo Punto: (4, 1), (8, 2), (12, 3), (16, 4), (20, 5). Alternativamente en Entrada: A = (4, 1), B = (8, 2), C = (12, 3), D = (16, 4), E= (20, 5). Recuerda que puedes hacer Zoom con Ctrl+Alt o la tecla Windows y la rueda del ratón. |
|
|
4. Traza una línea entre dos de los puntos dibujados con la herramienta Recta que pasa por Dos Puntos o escribe en Entrada: a=Recta[A, E].
Observa que la recta que obtenemos (-x+4y=0 o y= 5. Pasa por el origen: si
x=0, y= 6. Une todos los puntos: por ejemplo, en B = (8, 2): y = 2 = (1/4)*x = (1/4)*8 (2).
La idea es clara, para un número x de casas, necesito
|
Fíjate
y= |
|
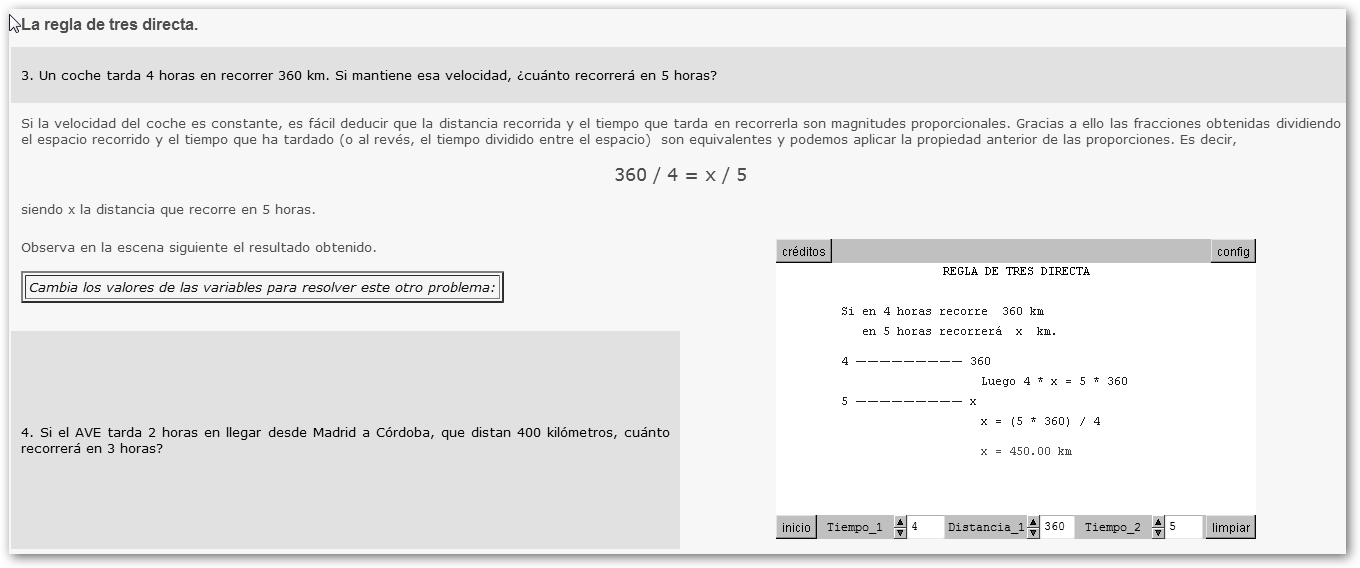
La regla de tres está estrechamente relacionada con este
concepto y se refiere a problemas del tipo: si un comerciante
vende 12 kilos de caracoles a 4 euros pero tu mamá te
dice Vemos en la ilustración la resolución. La solución es que me costará 1 euro. Hagámoslo con Calculadora inteligente en www.calculadorainteligente.com.br/calculadora, es una versión de prueba por 30 días para Windows que después seguirá funcionando pero nos molestará con los típicos avisos. Inícialo después de instalarlo desde Inicio, Todos los programas, Calculadora Inteligente, Calculadora Inteligente. |
Selecciona en el menú Opciones, Calcular Regla de Tres. Haz clic en Ejemplo 1 y Ejemplo 2 para obtener varios ejemplos de problemas. Indica las cantidades o valores implicados en el problema con sus correspondientes descripciones. Datos base: 12, 4 Cntd. O Valor (cantidades) en DATOS BASE; Caracoles, Euros en Descripcion; 3 Cntd. o Valor en HALLAR, indica que la incógnita son los Euros y pulsa en Calcular. |
|
|
|
Sin embargo, el mejor recurso sin duda para que puedas practicar no sólo los conceptos de proporcionalidad sino también la regla de tres directa y la proporcionalidad inversa es Descartes. Navega a la página de Descartes en www.educarm.es/cnice/descartes/Esp/, Unidades Didácticas, 1º y 2º de ESO, Funciones. La función de proporcionalidad.
 , una parte
o una porción formada por un número de partes sería
una fracción. En el ejemplo, la fracción 10/26
correspondería a dividir la tarta en 26 partes y quedarnos con 10.
, una parte
o una porción formada por un número de partes sería
una fracción. En el ejemplo, la fracción 10/26
correspondería a dividir la tarta en 26 partes y quedarnos con 10.

 en fracciones.
en fracciones. 




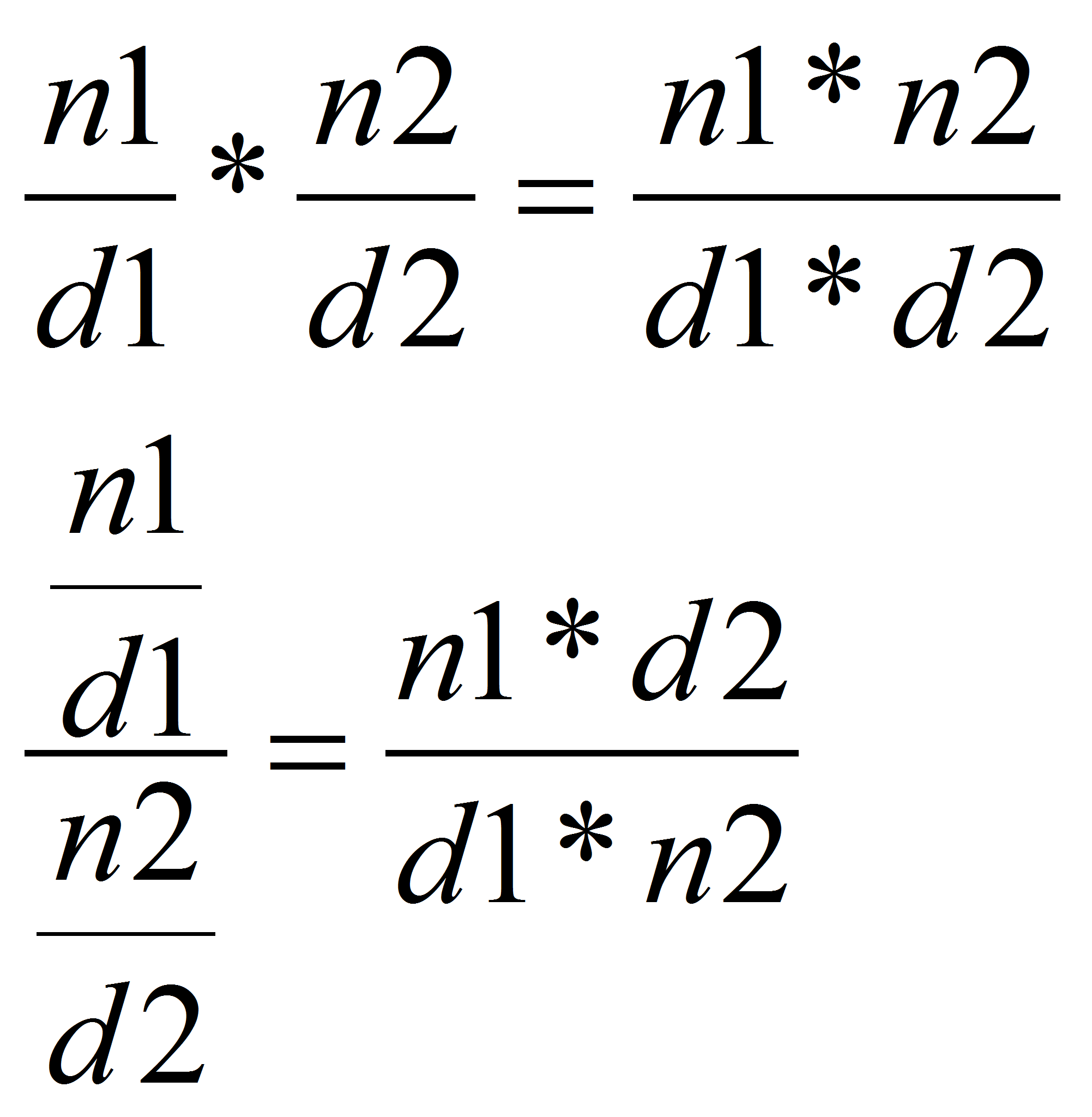

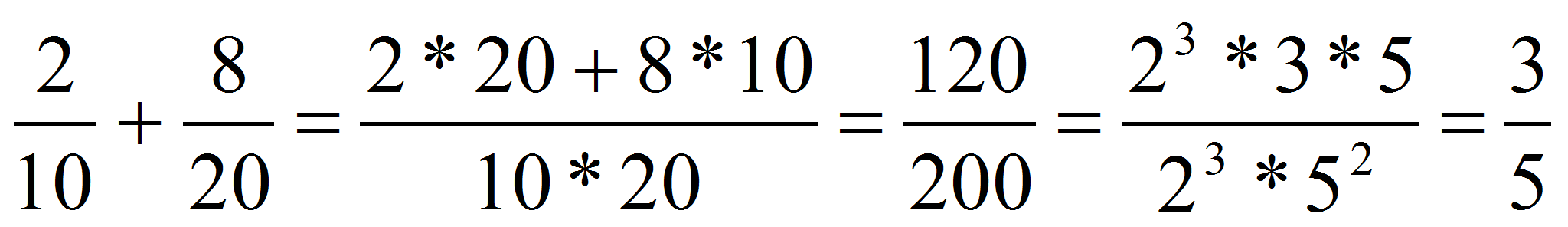
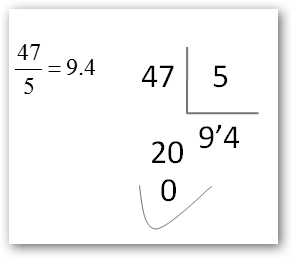

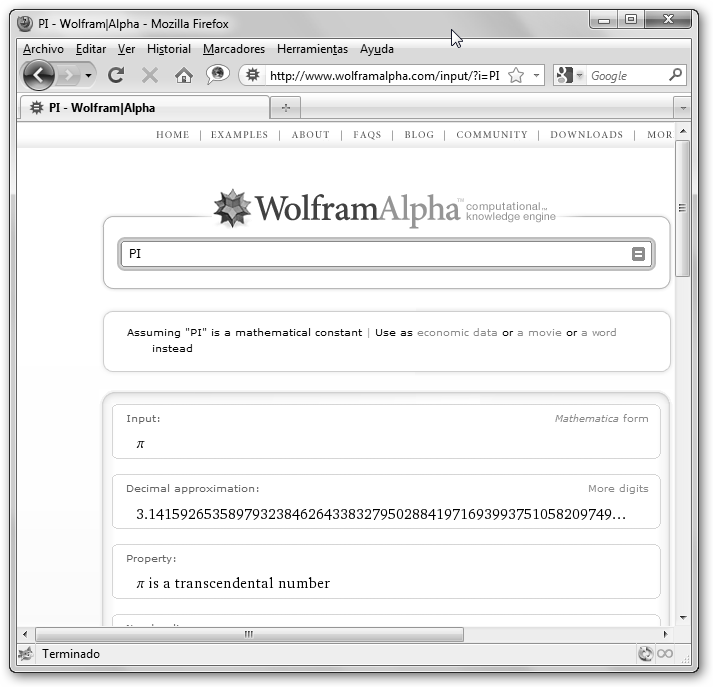
 ¡Los números decimales que no son exactos, tienen
infinitas cifras decimales y tampoco poseen un periodo no
pueden representarse como fracciones (no son racionales, no
pertenecen a Q) y se denominan irracionales!
¡Los números decimales que no son exactos, tienen
infinitas cifras decimales y tampoco poseen un periodo no
pueden representarse como fracciones (no son racionales, no
pertenecen a Q) y se denominan irracionales! sencillo: “¡Yo sí que los tendría
ordenados y más firmes que una vela!”
sencillo: “¡Yo sí que los tendría
ordenados y más firmes que una vela!”

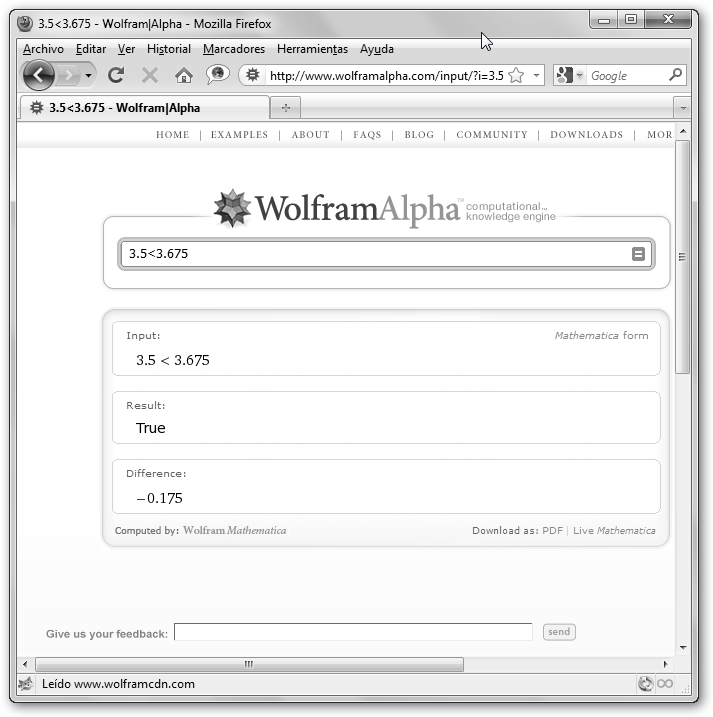

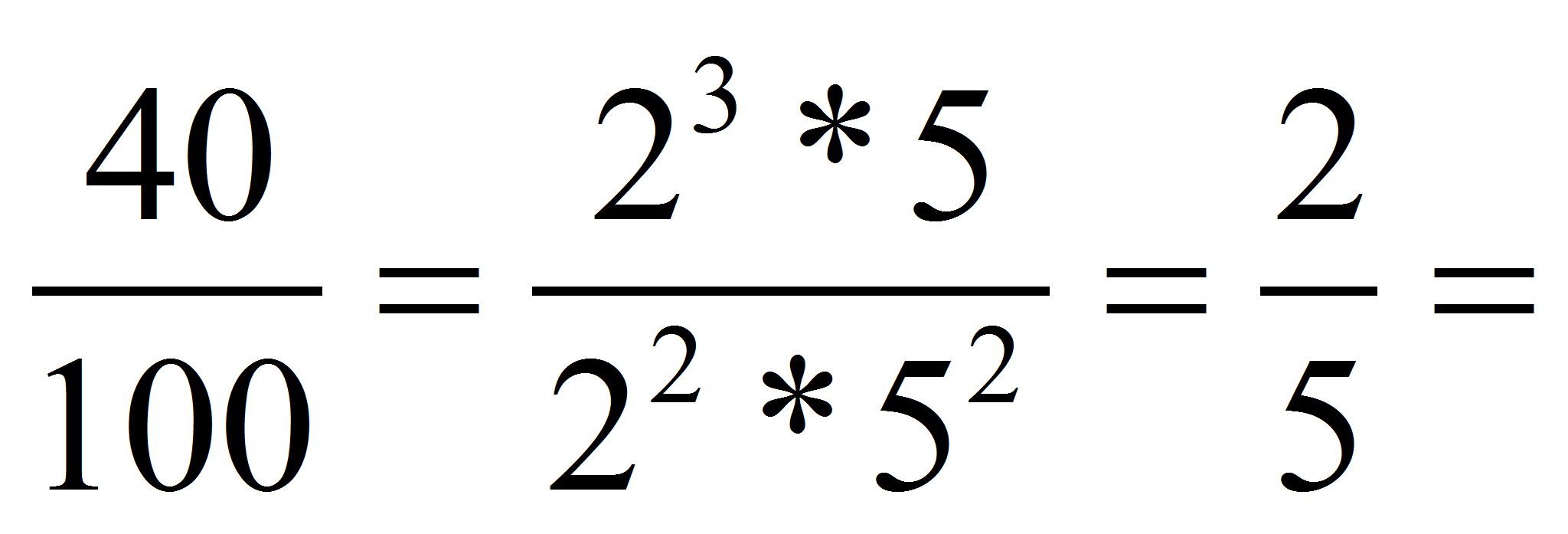 ) o un número decimal, en el ejemplo 0.4.
) o un número decimal, en el ejemplo 0.4.


 ¡yo que hago con tanto caracol! Yo sólo quiero 3
kilogramos.
¡yo que hago con tanto caracol! Yo sólo quiero 3
kilogramos.

