4. Números naturales y enteros. ¿Quién dijo miedo?
4.1 Números naturales: ¿cómo podríamos contar patitos sin ellos? 2
4.2 Contando y calculando con el ábaco. 2
4.3 Calculando los divisores de un número. 5
4.4. ¿Soy primo o si no quién soy? 7
4.5. Y a mí, ¿quién me factoriza? 10
4.7. Calculando potencias y raíces. 13
4.8 Trabajando con números enteros. 14
4.9 Un mapa conceptual para domesticar los números. 16
4.10 Los números tienen su historia… 19
4.1. Números naturales: ¿cómo podríamos contar patitos sin ellos?
Empecemos explicando que son los números
naturales. Se trata de un conjunto de números {1, 2, 3, 4,
5,…} que se utiliza para contar patitos ,
caracoles
,
caracoles o burros
o burros .
Bueno vale… ¡podemos contar más cosas! Se
representa por una N pero dibujada un poco más chula N
y es un conjunto infinito.
.
Bueno vale… ¡podemos contar más cosas! Se
representa por una N pero dibujada un poco más chula N
y es un conjunto infinito.
 .
Básicamente significa que si empiezas a escribir en una
libreta 1, 2, 3, 4, 5, 6, … y escribes horas y horas
.
Básicamente significa que si empiezas a escribir en una
libreta 1, 2, 3, 4, 5, 6, … y escribes horas y horas ,
al día siguiente continuas donde lo dejaste 10023, 10024,
10025,… y así un día y otro día y llegas
a un número “exagerado” 234211, siempre habrá
un chino
,
al día siguiente continuas donde lo dejaste 10023, 10024,
10025,… y así un día y otro día y llegas
a un número “exagerado” 234211, siempre habrá
un chino
 que pueda contar un número más
grande, por ejemplo 234212, 234123,…¿Y si llegó
a un billón? Pues, alguien dirá un trillón. ¿Y
un trillón? Pues, dos trillones.
que pueda contar un número más
grande, por ejemplo 234212, 234123,…¿Y si llegó
a un billón? Pues, alguien dirá un trillón. ¿Y
un trillón? Pues, dos trillones.
4.2. Contando y calculando con el ábaco.
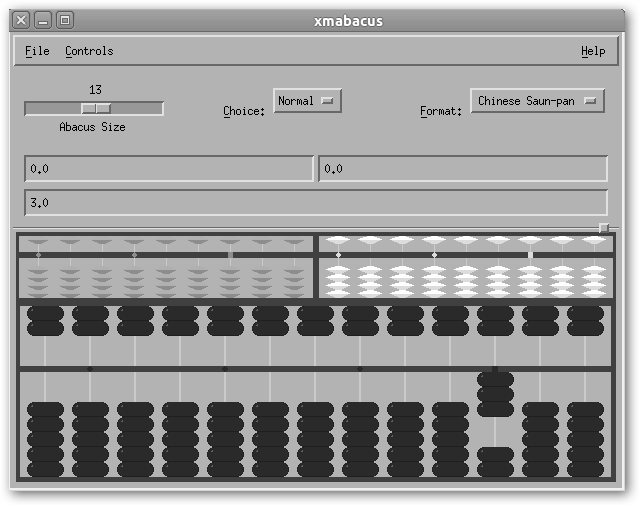
El ábaco es uno de las primeras herramientas que nuestros antepasados utilizaron para realizar cálculos sencillos (sumas, restas, multiplicaciones y divisiones) y es, en la actualidad, un excelente ejercicio para la mente y para enseñar y aprender las matemáticas más básicas.
El ábaco que utilizaremos es xmabacus que puedes instalar en Ubuntu desde Aplicaciones, Centro de software de Ubuntu, seleccionando e instalando xmabacus o en la consola (Aplicaciones, Accesorios, Terminal) tecleando sudo apt-get install xmabacus. Otra posibilidad es xabacus. Para la versión de Windows visita http://www.tux.org/~bagleyd/abacus.html y descarga el programa en el enlace xabacus at tux.org(http). No requiere instalación, basta con descomprimirlo en una carpeta de tu disco duro y lanzar wabacus.exe.
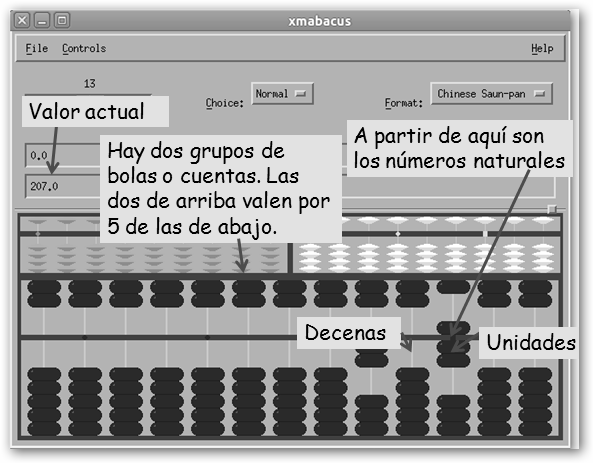
Normalmente construido de madera consiste en una serie de barras verticales y un travesaño horizontal que lo divide en dos secciones. En la zona o cubierta inferior se encuentran las bolas o cuentas que tienen como valor 1. En la superior, las cuentas o bolas que valen por 5. Observa en la figura que hemos contado doscientos siete (207) con dos cuentas inferiores (2) y una superior (5) en la varilla de las unidades y otras dos inferiores en la barra de las centenas (200). Luego, contemos: 2 + 5 + 200 = 207.
|
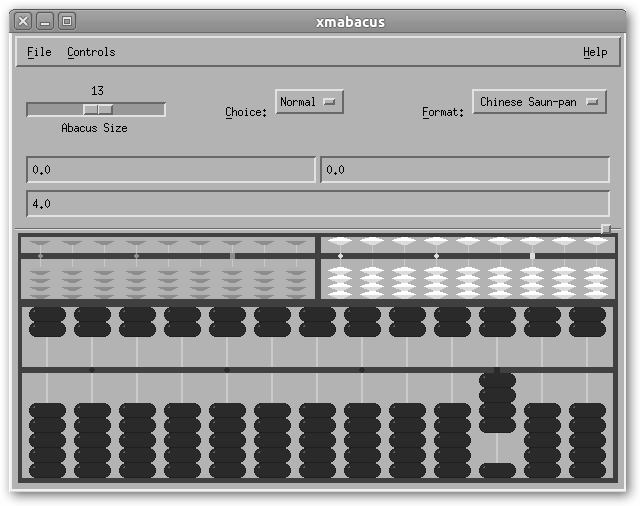
Sumemos 3 y 1. Primero, contamos tres unidades haciendo clic en tres cuentas en la varilla de las unidades. |
A continuación, contamos otra bola en la barra de las unidades y tenemos cuatro cuentas. Observa que xmabacus nos lo está indicando (4.0) y que también podemos contar con decimales. |
|
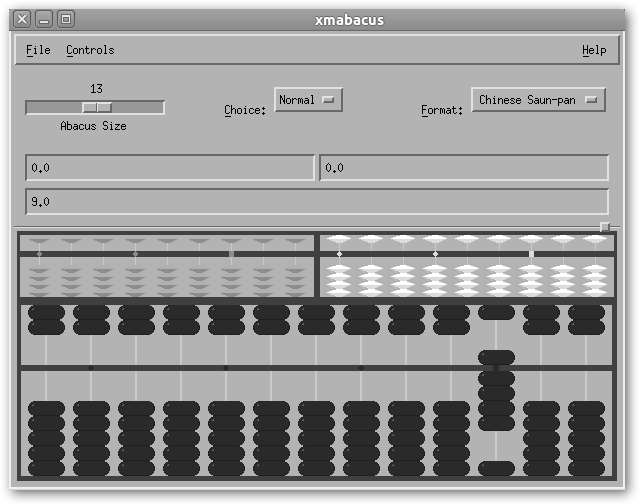
¿Y 4+5? Pues basta bajar una de las bolas de la cubierta superior para obtener 9. |
¿Y 9 + 8? ¡Ya la hemos liado, nos hemos quedado sin cuentas! |
|
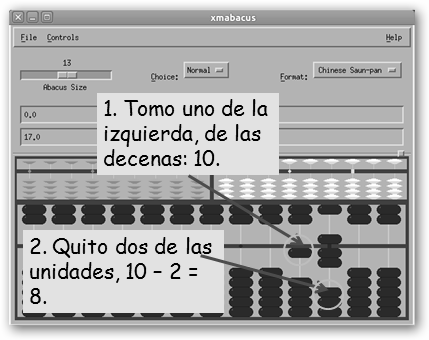
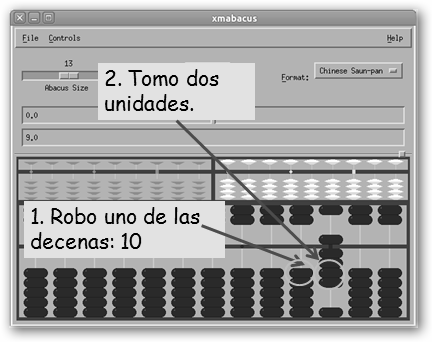
Restar es también bastante sencillo. Se ilustra en la figura: 17 (el resultado que habíamos obtenido previamente) – 8. Es deshacer lo ya andado, en este caso, primero quito una de las decenas (10) y cojo dos unidades (10-2=8), recuerda que sólo queríamos quitar 8, no diez. Tanto con xmabacus como con xabacus podemos contar con otros ábacos en el cuadro Format: coreano, ruso, japonés, etc. |
|
4.3. Calculando los divisores de un número.
Con los números naturales podemos realizar distintas operaciones: suma (+), resta (-), multiplicación (X) y división (/).
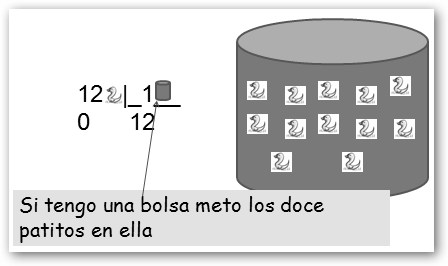
Ahora imagínate que quiero enviarle mi preciosa colección
de 12 patitos a nuestro amigo chino. Tengo bolsas de todos los
tamaños pero como soy un poco quisquilloso y maniático ,
me gustaría que en todas las bolsas viajen el mismo número
de patitos y que, por supuesto, viajen todos y no sobre ninguno.
¿Cómo lo hago?
,
me gustaría que en todas las bolsas viajen el mismo número
de patitos y que, por supuesto, viajen todos y no sobre ninguno.
¿Cómo lo hago?
|
|
|
|
|
|
|
|
|
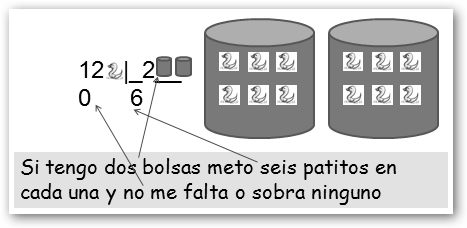
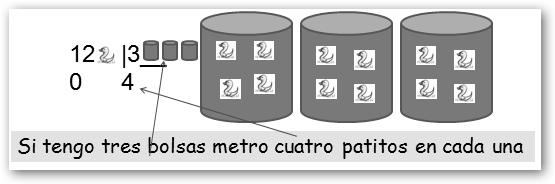
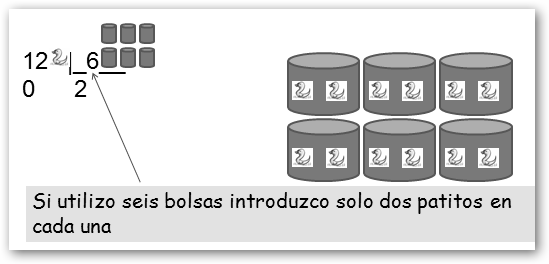
Por tanto podemos empaquetar 12 patitos en 1, 2, 3, 4, 6 y 12 bolsas sin que falten ni sobren patitos y en todas las bolsas viajan el mismo número de patitos: 12, 6, 4, 3, 2 y 1 respectivamente. ¡Ese es el concepto de divisor! En otras palabras, los divisores de un número son aquellos que lo dividen con resto cero. Si quisiéramos enviarlos en bolsas de 5, sería 12 dividido por 5 tendríamos el cociente 2 y el resto 2, es decir, en dos bolsas meteríamos 5 patitos pero nos faltan 2 que aunque se lo enviáramos a nuestro amigo en una tercera, ya no viajarían en el mismo número.
|
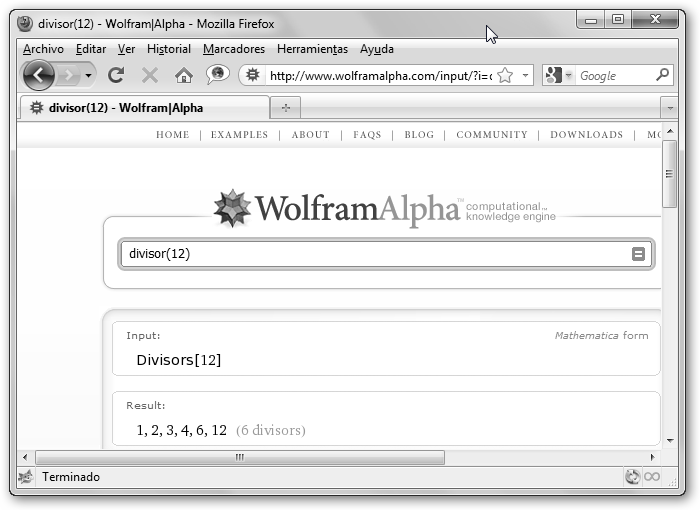
¿Y cómo se calculan los divisores de un número? Podemos utilizar los servicios de WolframAlpha en www.wolframalpha.com y solicitar los divisores de un número, por ejemplo 12, escribiendo divisores(12) tal como se muestra en la figura. |
|
|
Otra opción es utilizar Maxima. Se trata de un potente software que nos permite realizar cálculos simbólicos y numéricos, así como, graficar funciones en dos y tres dimensiones. Es libre (licencia GPL) y multiplataforma. La página del proyecto es maxima.sourceforge.net. Para disponer del programa en Windows navega por su portal Web a la sección Download, haz clic en el enlace Sourceforge download page (página de descargas de Sourceforge) y descarga la versión para Windows. En Ubuntu instala los paquetes maxima, xmaxima y wxmaxima desde el Centro de software de Ubuntu o en el terminal con sudo apt-get install maxima xmaxima wxmaxima (¡ojo!, maxima aquí no debe llevar tilde). |
|
|
|
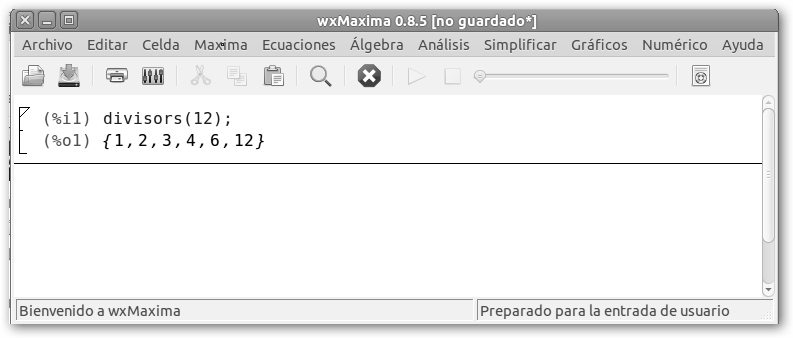
Inicia wxMaxima desde Inicio, Todos los programas, Maxima-5.22.1, wxMaxima en Windows y Aplicaciones, Ciencia, wxMaxima en Ubuntu. Escribe divisors(12); (o cualquier otro número del que quiera conocer sus divisores) y presiona simultáneamente las teclas INTRO (o retorno) y Control. También puedes seleccionar la opción Evaluar Celda(s) del menú Celda. |
|
La tercera alternativa es gMatESO. Existen algunas distribuciones que traen el programa ya pre-instalado. En el caso de Ubuntu descarga el paquete desde www.lubrin.org/gmateso, descomprímelo en tu carpeta personal y ejecuta ./gmateso-0.1/gmateso. En el menú Tema contienes las fichas matemáticas de las que consta gMatESO. |
|
|
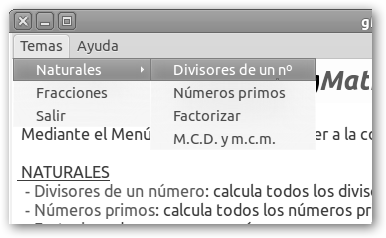
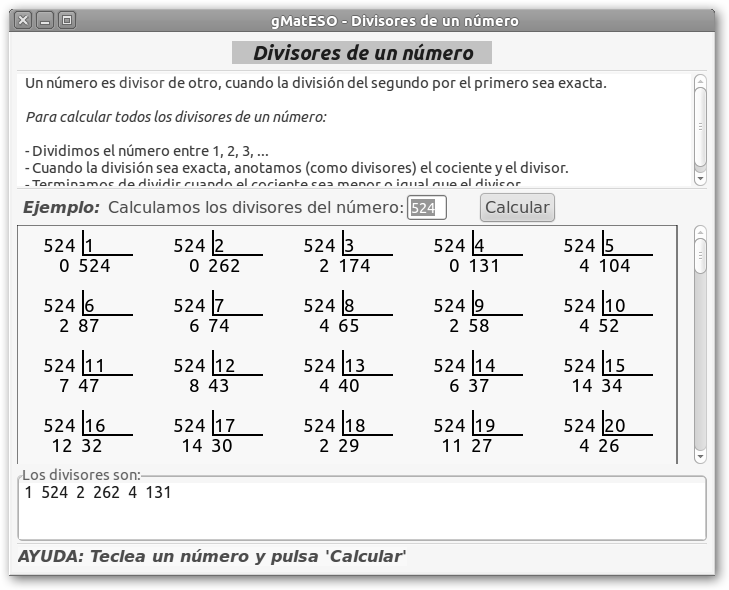
En este tema nos interesa Temas, Naturales pero también puedes aprender fracciones con este programa. Observa el detalle de la ficha Divisores de un número (Temas, Naturales, Divisores de un nº). |
Solo tienes que teclear un número y pulsar Calcular tal como te indica en la ayuda. |
4.4. ¿Soy primo o si no quién soy?
Existen dos tipos de números:
* Primos: aquellos que solo tienen
dos divisores distintos, él mismo y 1. Por ejemplo 1, 2, 3, 5, 7, etc.
 ¡No confundir con hacer el primo ni con el súper primo
de Rajoy (www.elprimoderajoy.org)!
¡No confundir con hacer el primo ni con el súper primo
de Rajoy (www.elprimoderajoy.org)!
* Compuestos: los números que no son primos, es decir, además de tener como divisores a 1 y a sí mismo, tienen otros divisores, por ejemplo 6, 12, 14, 24, 32, etc.
|
Si tu número
tiene crisis de identidad |
|
|
|
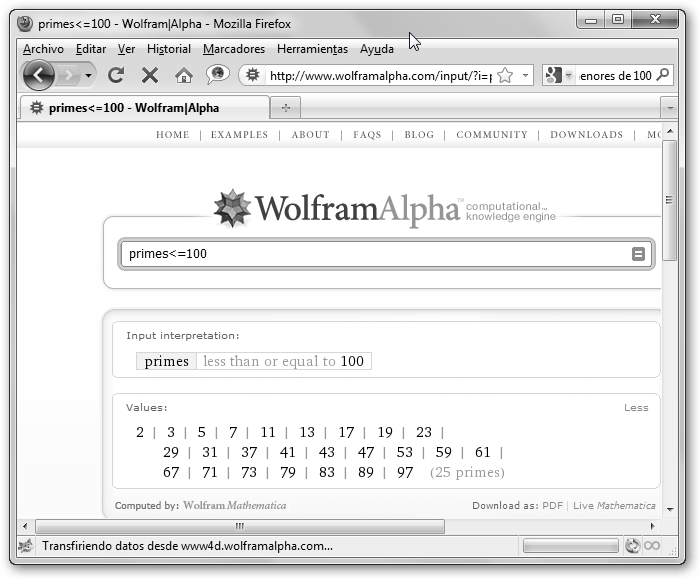
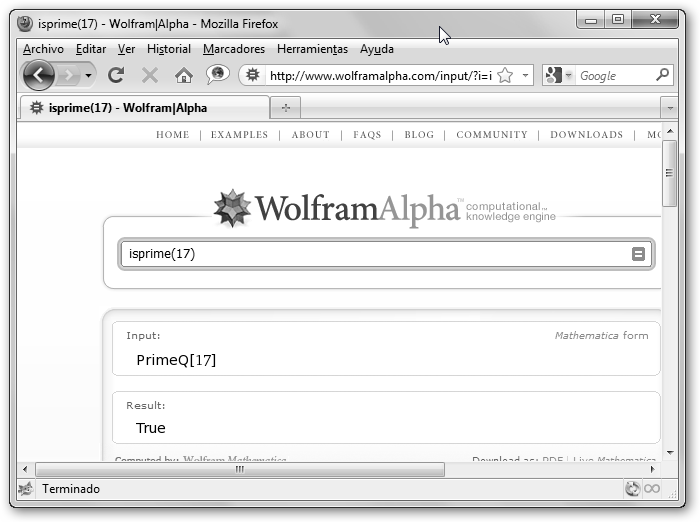
1. Pregúntale a wxMaxima: primep(miNumero). Por ejemplo primep(12) devuelve false, falso (tiene como divisores además del 1 y el 12, el dos, el tres, el cuatro y el seis). Si solicitamos primep(17) nos da true, verdadero pues 17 es primo. 2. Lanzar la consulta en WolframAlpha: isprime(miNumero), en la figura se muestra que 17 es primo. Si quieres saber los números primos del 1 al 100 teclea primes<=100, cambia 100 por 1000 para obtener los números primos del 1 al 1000. |
¡Por cierto, me equivoqué no tengo 12 patitos
 sino
17! ¿Cómo podremos enviarle mi preciosa colección
de 12 patitos a nuestro amigo chino
sino
17! ¿Cómo podremos enviarle mi preciosa colección
de 12 patitos a nuestro amigo chino
 en bolsas conteniendo siempre el mismo número de patitos? Pues
solo podemos enviárselos en paquetes individuales (1 es
divisor de 17) o en una única bolsa (17 es divisor de sí
mismo).
en bolsas conteniendo siempre el mismo número de patitos? Pues
solo podemos enviárselos en paquetes individuales (1 es
divisor de 17) o en una única bolsa (17 es divisor de sí
mismo).
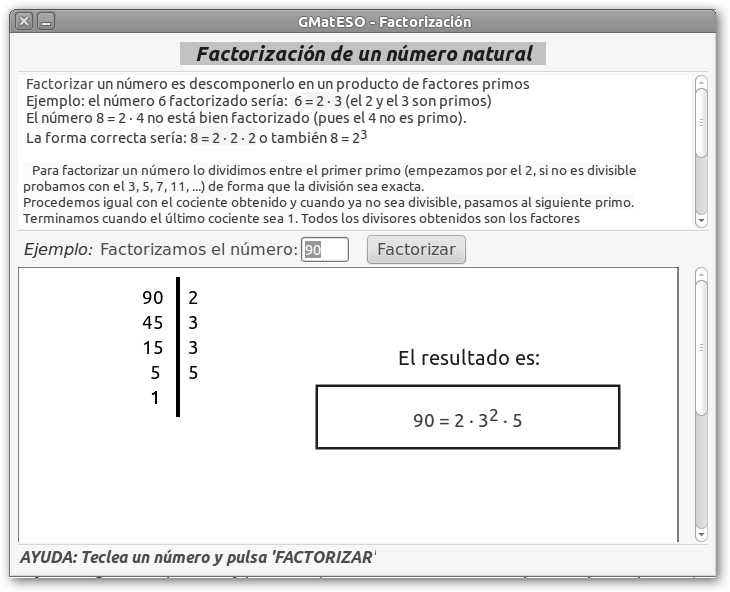
4.5. Y a mí, ¿quién me factoriza?
|
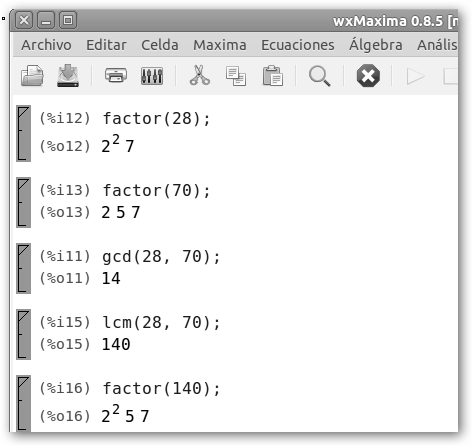
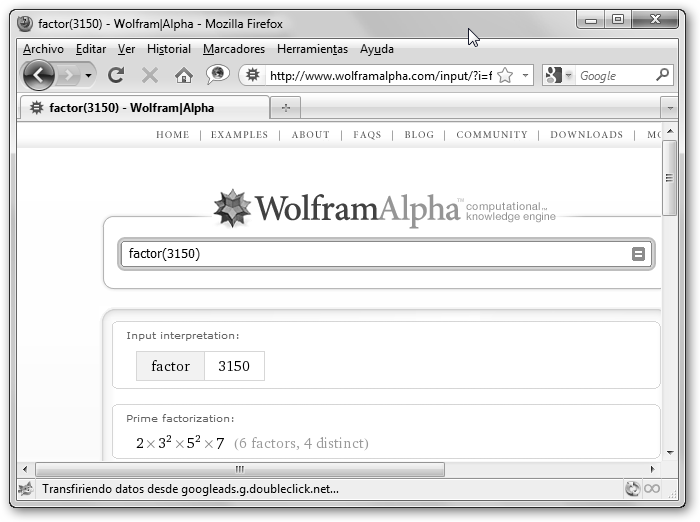
La factorización de un número natural es la descomposición de éste en sus números primos, es decir, es expresar el número como producto de sus factores primos. Se muestra en: * wxMaxima: factor(28) sería 22*7. * WolframAlpha: factor(3150) es 2*32*52*7. * GMatESO en el menú Temas, Naturales, Factorizar, teclea el número y haz clic en el botón Factorizar. |
|
|
|
|
Observa que como 90 termina en cero dividimos por 2 y obtenemos 45. Como la suma de las cifras o dígitos de 45 (4+5=9) es múltiplo de 3 dividimos por 3 y obtenemos 5, con lo que acabamos pues 5 es primo.
Las reglas de divisibilidad indican cuando un número es divisible. Un número es divisible por 2 si termina en par (0, 2, 4, 6, 8), por 3 si la suma de sus dígitos es múltiplo de 3, por 5 si termina en 0 o en 5.
4.6. M.c.d y m.c.m.
|
El máximo
común divisor de varios números (12, 28) es el mayor
|
El mínimo común múltiplo de varios números (12, 28) es el menor de sus múltiplos comunes. Se obtiene multiplicando los factores primos comunes (2) y no comunes (3, 7) con el mayor exponente (22, 3, 7). En el ejemplo se solicita a wxMaxima tanto el máximo común divisor (gcd(12, 28);) como el mínimo común divisor (lcm(12, 28);). |
|
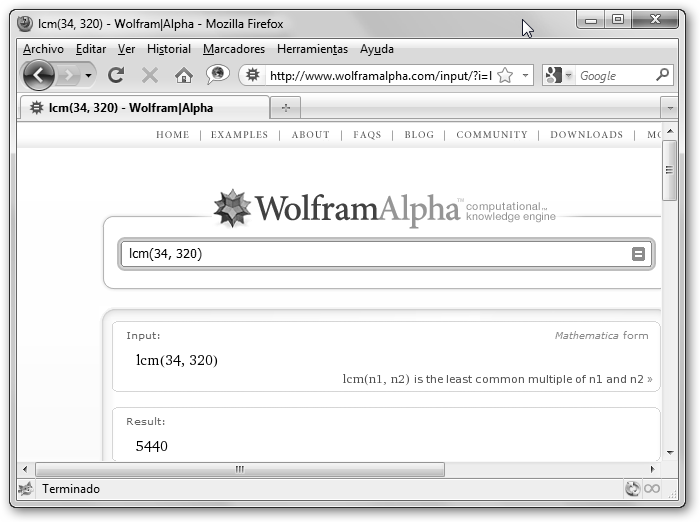
En Wolfram Alpha solicitamos también ambos, la sintaxis es la misma pero sin el punto y coma final, sería: gcd(34, 320) y lcm(34, 320). Observa que 34=2*17 y 320=26*5. Por tanto, el máximo común divisor es 2 (el único factor común con el menor exponente) y el mínimo común divisor sería 26*5*17=5440 pues el único factor común es 2 y tiene como máximo exponente el 6 (en 320) y los factores no comunes son el 17 y el 5. ¿Por qué
lcm y gcd? Pues porque son las siglas de least common multiple y
greatest common divisor que significan mínimo común
múltiplo y máximo común divisor en inglés |
|
|
|
Imagínate que queremos enviarle
a nuestro amigo, no sólo 12  sino también 28
sino también 28
 .
.
¿Cuál es el mayor número de bolsas que podemos enviarle suponiendo que queremos que en cada una haya el mismo número de cada clase? ¡Sí!, lo has adivinado 4 bolsas (el máximo común divisor) conteniendo cada una de ellas 3 patitos y 7 conejos.
4.7. Calculando potencias y raíces.
La potencia de un número es dicho número (que
llamaremos base) multiplicado por sí mismo un cierto número
de veces (que lo bautizaremos como exponente, ¡qué
nombre más feo pobrecito!), se expresa así:
baseexponente. Por ejemplo 25=2*2*2*2*2=32 y se
lee “dos elevado a cinco es 32”. Imagina que envío
a mi amigo 7 paquetes con 7 bolsas cada una y, además, cada
caja contiene 7
 ¿Cuántos conejos le envío? Pues 7*7*7=73=343.
Por cierto, cualquier número elevado a 0 es 1:
20=30=40=…=1938430=1,
así si estás cansado de alguien y no quieres utilizar
la expresión “multiplícate por cero” porque
está muy vista, también puedes decirle “elévate
a cero”.
¿Cuántos conejos le envío? Pues 7*7*7=73=343.
Por cierto, cualquier número elevado a 0 es 1:
20=30=40=…=1938430=1,
así si estás cansado de alguien y no quieres utilizar
la expresión “multiplícate por cero” porque
está muy vista, también puedes decirle “elévate
a cero”.
La raíz cuadrada de un número es aquel que elevado al
cuadrado es igual a nuestro número, más formalmente:
![]() si raíz2=número. Así las raíces
de 4, 9, 16 y 25 son 2, 3, 4 y 5 respectivamente pues 22=4,
32=9, 42=16 y 52=25. La raíz
enésima de un número
si raíz2=número. Así las raíces
de 4, 9, 16 y 25 son 2, 3, 4 y 5 respectivamente pues 22=4,
32=9, 42=16 y 52=25. La raíz
enésima de un número
![]() es aquel cuya potencia enésima es igual a nuestro número,
es decir, raízn=numero.
es aquel cuya potencia enésima es igual a nuestro número,
es decir, raízn=numero.
|
|
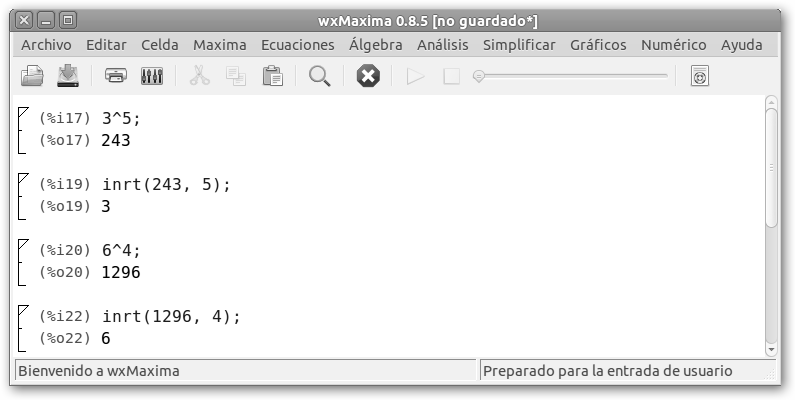
En wxMaxima se solicita la potencia de un número escribiendo base^exponente. En el ejemplo hemos tecleado 3^5, es decir, 35 y nos devuelve 243. Luego, hemos pedido la raíz quinta de 243 (inrt(243, 5)) y devuelve 3. La raíz cuadrada de 9 sería sqrt(9); |
|
|
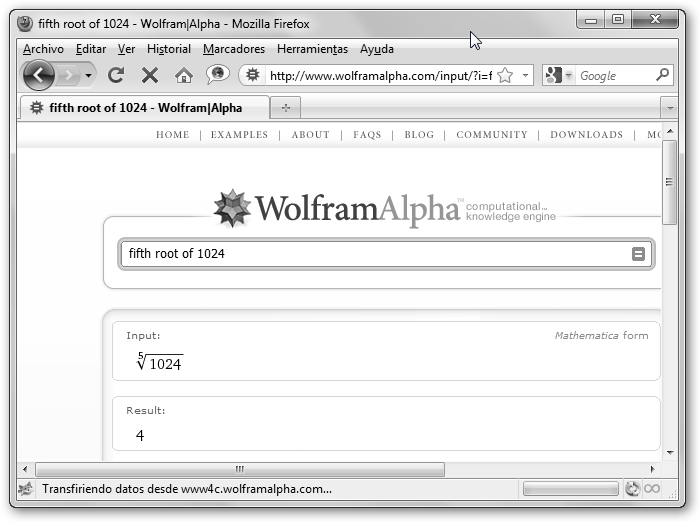
En WolframAlpha la potencia se escribe de la misma forma base^exponente, sin embargo, observa como la raíz quinta de 1024 se solicita con fifth root of 1024. Veamos
otros ejemplos: raíz cuadrada (sqrt
4), third
root of 8 ( |
4.8. Trabajando con números enteros.
|
¿Para qué sirven los números enteros negativos? A ver… pensemos… 1. Para liarnos y suspender
más fácilmente
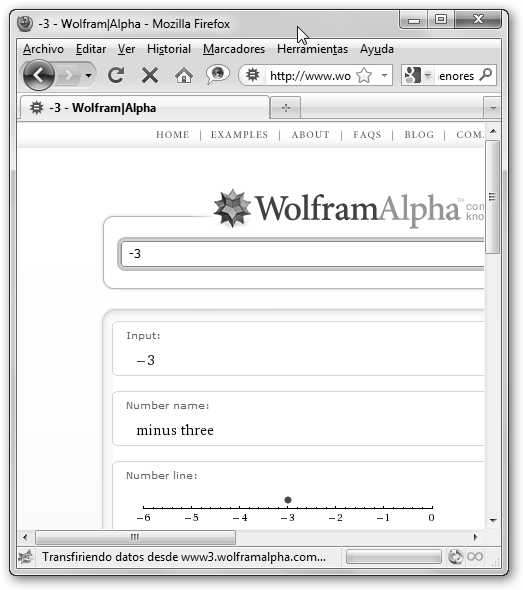
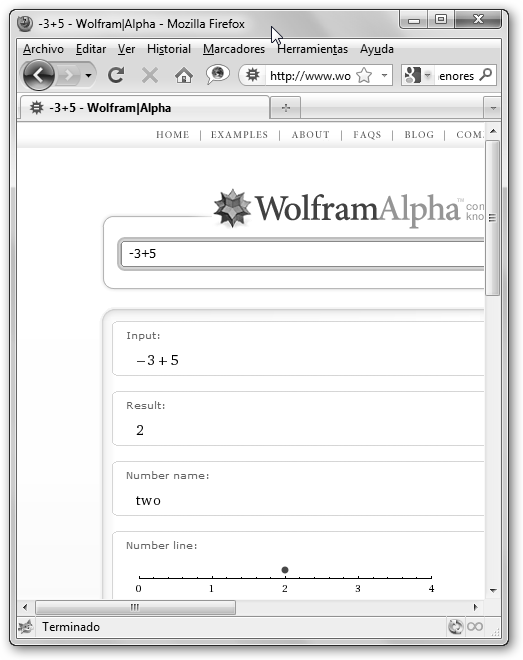
2. Imagínate que en Moscú tienen tres grados bajo cero (-3) a las 7 de la mañana y sube a las 2 de la tarde 5 grados. ¿Qué temperatura tienen entonces? Pues -3+5=2º, dos graditos. En la pantalla inferior se ilustra cómo realizarlo con WolframAlpha. 3. Ahora imagina que tenemos 40 patitos, pero debemos 7 patitos en las siguientes ciudades: Londres, Madrid, París, Berlín, Roma, Santiago, Barcelona y Málaga. ¿Cuántos patitos nos quedan? |
Detalle de la representación en la recta real del número negativo -3, observa que se sitúa a la izquierda del cero. |
|
|
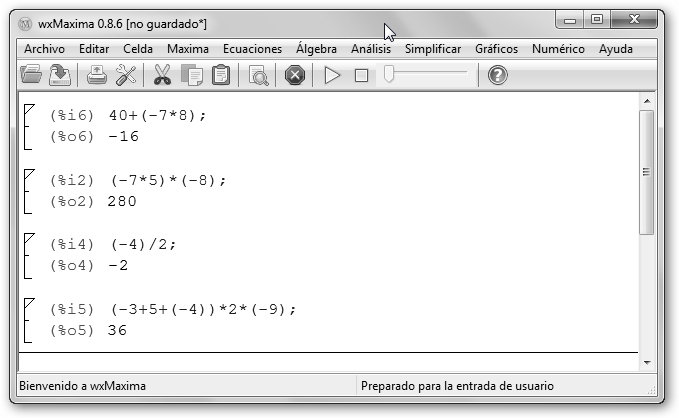
Tenemos 40, luego es 40 más algo. El hecho de deber 7 patitos lo representamos por -7. Si debemos en 8 ciudades, lo que realmente tenemos que entregar es (-7*8). Observa el resultado final -16, es decir, nos faltan 16 patitos incluso cuando entreguemos todos los que tenemos. A continuación, se ilustran más operaciones con números enteros. |
|
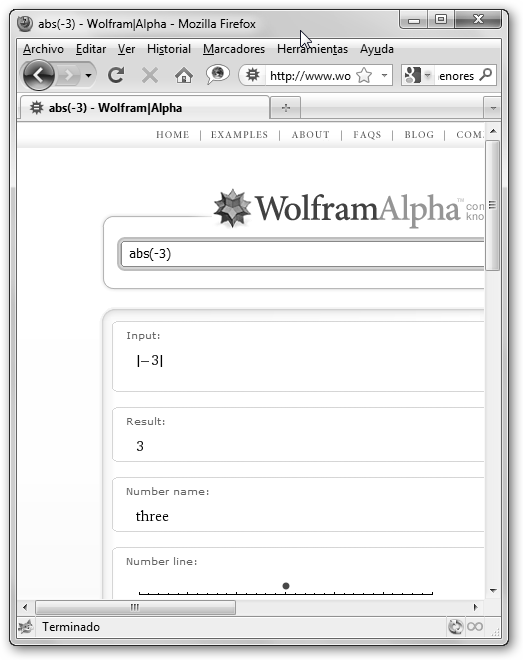
¿Y el valor absoluto de un número? Es el valor de un número sin importar cuál es su signo. ¿Cómo lo calculamos? * Wolfram Alpha: abs(-3). Observa la representación: |-3| con dos barras verticales “escoltando” al número. * Maxima: abs(-3); con el punto y coma al final. |
|
4.9. Un mapa conceptual para domesticar los números.
Cuando estudiamos matemáticas nos enseñan los números naturales, enteros, reales, decimales, fraccionarios, etc. A veces, es difícil reconocer las relaciones que existen entre dichos conceptos y nos parecen lecciones o temarios inconexos sin relación alguna aparente. Los mapas conceptuales vienen en nuestro auxilio, a ayudarnos a organizar nuestro conocimiento, permitiéndonos un aprendizaje más constructivo y significativo, lo que nos permitirá resolver problemas específicos matemáticos o de la vida cotidiana.
Puedes utilizar lápiz y papel o utilizar programas como FreeMind (freemind.sourceforge.net), VYM (www.insilmaril.de/vym, no disponible para Windows), CMapTools (cmap.ihmc.us), Visual Understanding Environment (vue.tufts.edu), Dia (projects.gnome.org/dia), etc. Para ejemplificar utilizaremos FreeMind. Realiza los siguientes pasos:
1. Descárgalo e instálalo. En Windows navega a freemind.sourceforge.net y pulsa en download. En Ubuntu instala el paquete freemind o búscalo en el Centro de Software de Ubuntu.
|
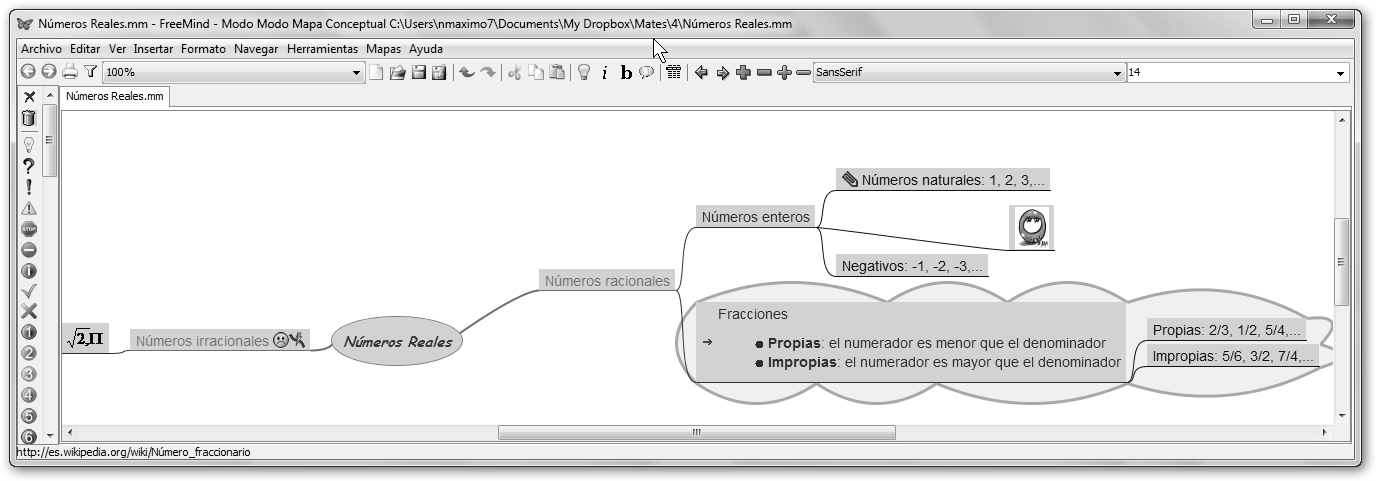
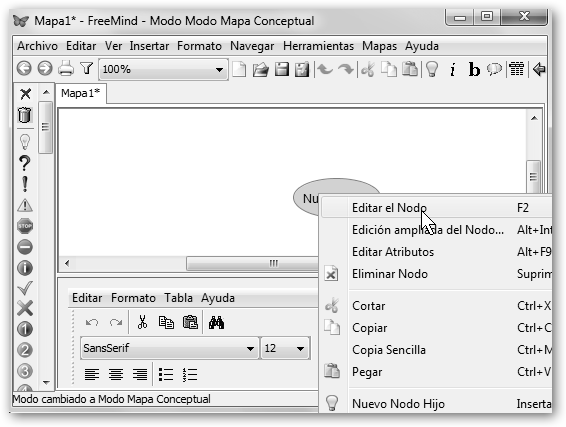
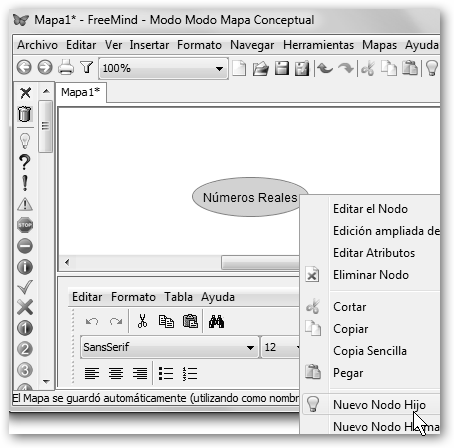
2. Lánzalo desde su entrada en el menú Oficina en Ubuntu o desde Inicio, Todas las aplicaciones, FreeMind, FreeMind en Windows. 3. La burbuja central es el concepto o idea central sobre el que gira todo el mapa conceptual. Haz clic sobre ella con el botón derecho, en el menú contextual selecciona la opción Editar el Nodo y modifica el texto por “Números Reales”. |
|
|
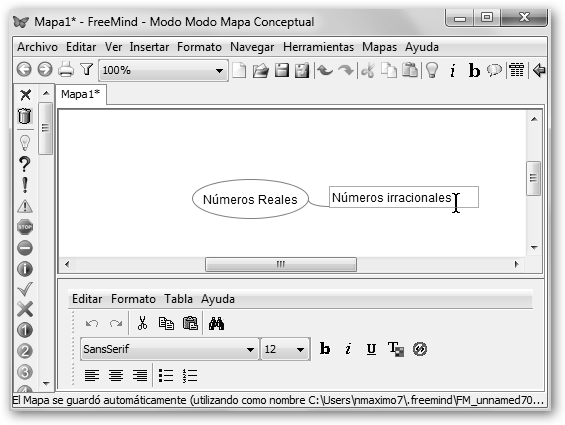
4. Pulsa nuevamente sobre la burbuja y selecciona en esta ocasión Nuevo Nodo Hijo. Escribe “Números irracionales” tal como se ilustra en la figura inferior. 5. Vuelve a repetir la operación: haz clic en Números Reales, selecciona Nuevo Nodo Hijo y teclea “Números racionales”. 6. A continuación, sobre los nuevos nodos creamos nodos hijos, es decir, sobre los números racionales creamos dos ramas: “Números enteros” y “Fracciones”. |
|
|
|
7. En el menú Archivo, selecciona Guardar para almacenar tu mapa conceptual en un archivo y no perder tu trabajo. |
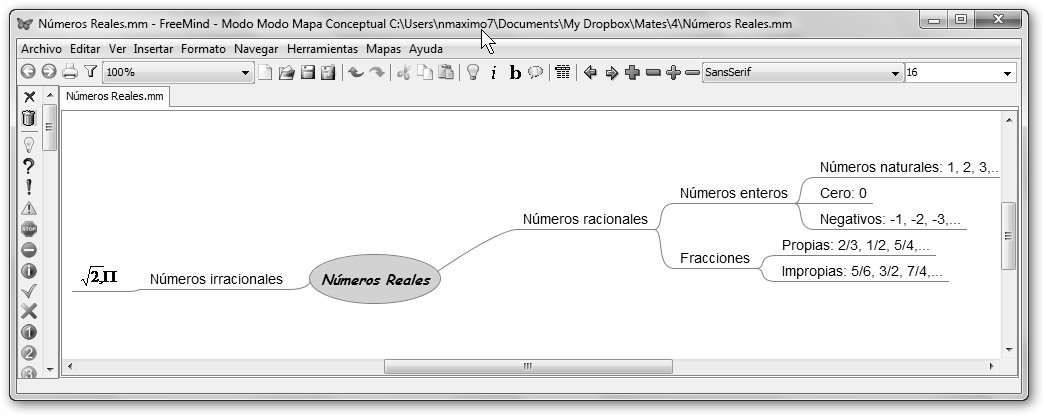
¿Qué
hemos realizado? Pues un mapa conceptual cuyo concepto central son
los números reales. Éstos se clasifican en números
irracionales (![]() etc.)
y en números racionales. A su vez los números
racionales pueden ser enteros o fracciones, los enteros son los
números naturales (1, 2, 3,…), el cero (0) y los
negativos (-1, -2, -3,…) y las fracciones pueden ser propias
(2/3, 1/2, 5/4) o impropias (5/6, 3/2, 7/4).
etc.)
y en números racionales. A su vez los números
racionales pueden ser enteros o fracciones, los enteros son los
números naturales (1, 2, 3,…), el cero (0) y los
negativos (-1, -2, -3,…) y las fracciones pueden ser propias
(2/3, 1/2, 5/4) o impropias (5/6, 3/2, 7/4).
|
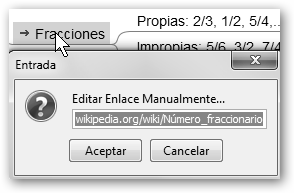
Sin embargo, el mapa aún puedes dotarlo de más contenido para que te sea más sencillo de comprender y memorizar los conceptos implicados. Una idea es incluir enlaces a páginas Web donde los expliquen. En la figura se ha seleccionado el nodo Fracciones y en el menú contextual hemos pulsado sobre Insertar, Enlace (Campo de Texto)… y se ha copiado en el cuadro de texto la URL o dirección de la entrada relativa a Fracciones de la Wikipedia. |
Si haces clic sobre Fracciones, se lanzará el navegador y mostrará la página Web que hayamos indicado. |
|
Podemos también, haciendo clic sobre un nodo: * Añadir imágenes: Insertar, Imagen (Seleccionar archivo u enlace)…) e iconos (Iconos). * Cambiar el estilo de todo el mapa o de un nodo: 1. Selecciona todos los nodos: Editar, Selecciona Todos los Visibles; 2. Cambia el estilo: Estilo Físico, MindMap1 u otro que te guste más. * Editar un nodo e incluir información adicional: Editar el Nodo. * Convertir el mapa a una imagen o un documento PDF desde el menú Archivo, opción Exportar, selecciona Como PNG…, Como JPEG… o Como PDF… * Imprimirlo: Archivo, Imprimir, etc. |
|
4.10. Los números tienen su historia…
4.10.1. Matemáticas recreativas
¿Qué son para ti los números? Para algunos es más que una representación abstracta o expresión de una cantidad. Para los pitagóricos los números eran el principio de todas las cosas y existe además una “ciencia metafísica” (pseudociencia), la numerología, que estudia el significado oculto de los números.
Cada número tiene además su historia: 0,1 son los
elementos neutros para la suma y la multiplicación
respectivamente; 2 es el único primo par; 7 el número
perfecto obtenido con la suma del 3, lo divino (Dios, uno y trino)
y 4 (lo terrenal); Π es la relación entre la longitud de
una circunferencia y su diámetro (en pidays.jtey.com
puedes calcular tu edad en años Π) y nadie puede escribir
todas sus cifras decimales (bueno Chuck Norris sí); 0, 1, i y e quedan hermanados con la identidad de Euler
(eiΠ+1=0);
sí); 0, 1, i y e quedan hermanados con la identidad de Euler
(eiΠ+1=0);
![]() la longitud de la hipotenusa de un triángulo rectángulo
cuyos catetos valen 1; el número áureo
la longitud de la hipotenusa de un triángulo rectángulo
cuyos catetos valen 1; el número áureo![]() aparece en las proporciones de numerosos objetos de la naturaleza, el
cuerpo humano, el arte, la arquitectura, etc.; 666 es el signo de la
bestia, del anticristo; un gugol es un número como que muy
grande
(10100), 13 (lo siento, doce más uno), 42
(la respuesta al sentido de la vida, el universo y todo lo demás).
Por haber, hay hasta números imaginarios (i), vampiros
(pueden ser expresados como producto de dos números, llamados
colmillos, obtenidos a partir de sus dígitos: 1395=15*93,
2187=27*81), narcisistas (iguales a la suma de sus cifras
elevadas a la potencia del número de sus dígitos:
370=33+73+03,153=13+53+33),
omirp (primo cuyo reflejado especular –o al darse la
vuelta- es también primo: 17, 71; 37, 73), capicúas
(se leen igual de izquierda a derecha --> que
de derecha a izquierda <-- : 181,
1551), eróticos (69, esto prefiero no explicarlo),
perfectos (iguales a la suma de sus divisores propios:
6=1+2+3, 28=1+2+4+7+14), triangulares (el resultado de sumar
los naturales: 1=1, 3=1+2, 6=1+2+3), felices (49, 97),
cíclicos (142857), amigos, sociables,
afectivos… Bueno, todo era para decir que: ¡las
matemáticas son divertidas y mágicas!
aparece en las proporciones de numerosos objetos de la naturaleza, el
cuerpo humano, el arte, la arquitectura, etc.; 666 es el signo de la
bestia, del anticristo; un gugol es un número como que muy
grande
(10100), 13 (lo siento, doce más uno), 42
(la respuesta al sentido de la vida, el universo y todo lo demás).
Por haber, hay hasta números imaginarios (i), vampiros
(pueden ser expresados como producto de dos números, llamados
colmillos, obtenidos a partir de sus dígitos: 1395=15*93,
2187=27*81), narcisistas (iguales a la suma de sus cifras
elevadas a la potencia del número de sus dígitos:
370=33+73+03,153=13+53+33),
omirp (primo cuyo reflejado especular –o al darse la
vuelta- es también primo: 17, 71; 37, 73), capicúas
(se leen igual de izquierda a derecha --> que
de derecha a izquierda <-- : 181,
1551), eróticos (69, esto prefiero no explicarlo),
perfectos (iguales a la suma de sus divisores propios:
6=1+2+3, 28=1+2+4+7+14), triangulares (el resultado de sumar
los naturales: 1=1, 3=1+2, 6=1+2+3), felices (49, 97),
cíclicos (142857), amigos, sociables,
afectivos… Bueno, todo era para decir que: ¡las
matemáticas son divertidas y mágicas!
|
|
¿Sabes lo que es la triscaidecafobia? La
fobia, el miedo irracional o incluso pánico que algunos
padecen
|
|
|
|
4.10.2. Sistemas de numeración en la antigüedad.
Más interesante aún es conocer que existieron otros sistemas de numeración en la antigüedad diferente al sistema decimal actual. Con WolframAlpha podemos convertir un número dado a los sistemas de numeración romano, griego, maya y babilónico, incluso nos permite pasar de un sistema a otro (de romano a babilónico: XIX to Babylonian). En gwydir.demon.co.uk/jo/numbers además de los sistemas de numeración mencionados podremos pasar los números al sistema egipcio (no posicional), chino y árabe. Cuenta también con una sección dedicada a los métodos e instrumentos utilizados en la antigüedad para realizar cálculos.
El sistema de numeración griego es decimal como el nuestro pero con letras, así α, β, , δ,… representan el uno, el dos, el tres, el cuatro,… Para las decenas tenemos otras letras, así como, para las centenas.

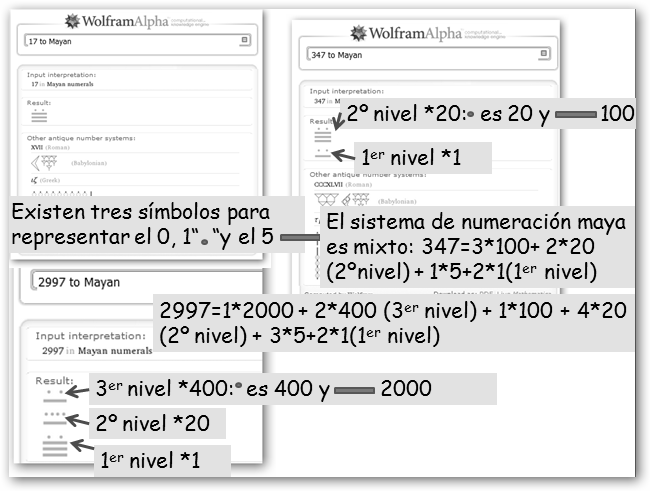
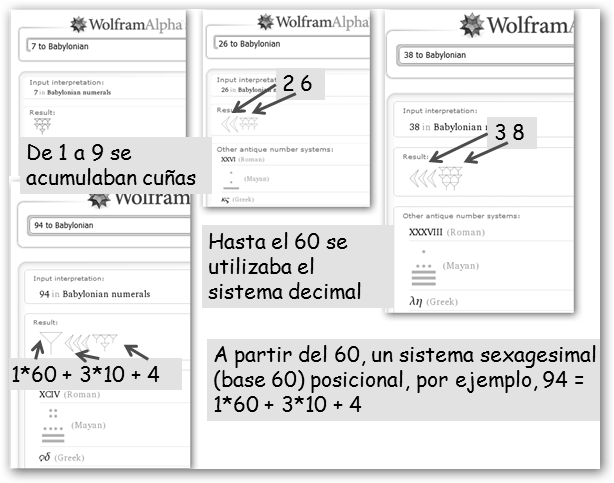
Otros sistemas de numeración han sido bastante más complicados. En el sistema maya la base es el 20, los números se representan de abajo a arriba y hay que multiplicar el valor de cada cifra por 1 en el primer nivel (200, el punto es 1, la línea 5), 20 en el segundo (201, el punto es 20, la línea 20*5=100), 400 en el tercero (202, el punto es 400, la línea 400*5=2000). En el babilonio tenemos un sistema decimal hasta el 60 y sexagesimal a partir de dicho número.



 y no sabe
quién es te proponemos dos opciones.
y no sabe
quién es te proponemos dos opciones. 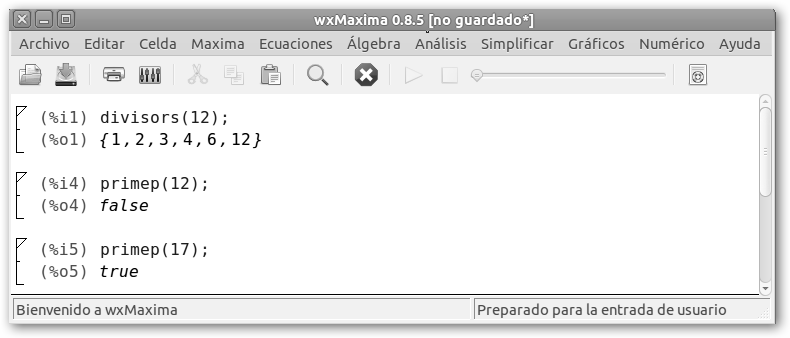
 divisor, es decir, “el
mayor número que los divide sin dejar resto” (Wikipedia,
es.wikipedia.org/wiki/Máximo_ común_divisor).
¡Ay!, pensé que era sin dejar rastro
divisor, es decir, “el
mayor número que los divide sin dejar resto” (Wikipedia,
es.wikipedia.org/wiki/Máximo_ común_divisor).
¡Ay!, pensé que era sin dejar rastro
 . Se obtiene multiplicando los
factores primos comunes de los dos números con el menor
exponente (en el ejemplo 22).
. Se obtiene multiplicando los
factores primos comunes de los dos números con el menor
exponente (en el ejemplo 22).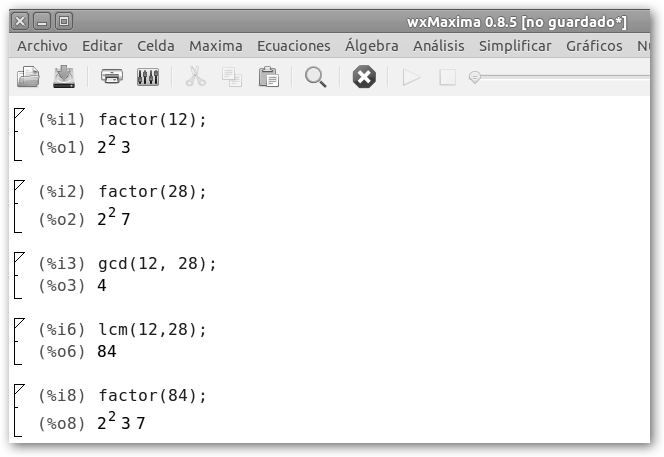
 respectivamente.
respectivamente.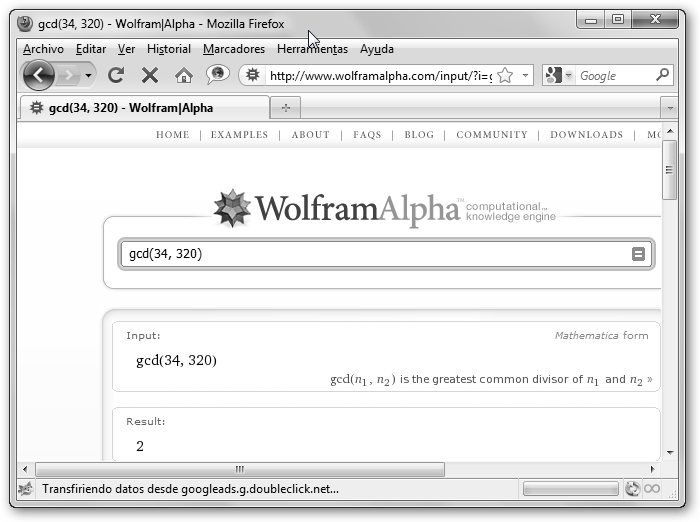
 .
.

 al número 13.
al número 13.