12. Matemáticas con Python II
12.2. ¡Sin límites! Implementación y representación gráfica del teorema de Bolzano
12.4. Visual Python, animaciones y geometría en 3D
12.5. Introducción a la Programación Orientada a Objetos
12.6. Herencia en Python: “P.O.O a toda potencia”
12.7. Programación funcional en Python
12.1. Python y Sage.
Ya hemos hablado de Sage. Si quieres profundizar, un buen manual de Sage lo encontrarás en la dirección http://www.sagemath.org/doc/tutorial/index.html.
|
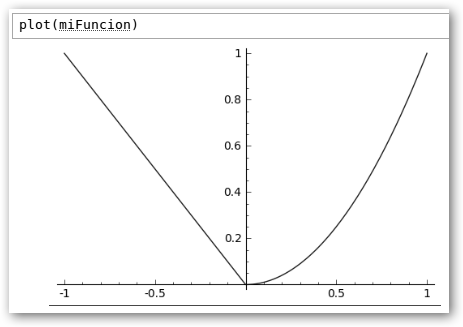
Lo que nos interesa en este momento es que podemos incrustar código Python en Sage. En el ejemplo, definimos la siguiente función a trozos: miFuncion(x)=
Sin embargo, aún
hay más 1. Editamos un archivo con extensión .py en una máquina con Sage instalado (por ejemplo, su máquina virtual). 2. Escribimos el siguiente código: (las almohadillas “#” son comentarios) #!/usr/bin/env sage -python
import sys from sage.all import * # Importamos las librerías necesarias. […] a, b, c, x = var(‘a b c x’) a = sage_eval(sys_argv[1]) b = sage_eval(sys_argv[2]) #Indicamos que las variables a, b, c y x serán utilizadas; las tres primeras serán inicializadas con el 2º, 3er y 4º argumento que se le pase al script. Nuestra función es un script que será invocado como sage –python miSage.py 24 -120 144 1 4. La llamada al script es sage –python miSage.py y los argumentos son: 24 (sys_argv[1]) -120 (sys_argv[2]) 144 1 4 |
|
|
|
|
||
|
Considera: el operador suma “+” es la concatenación de cadenas de caracteres: “a e i “ + “o u” será “a e i o u”; str(a) convierte a texto el número “a”; divisors(a) es la llamada a la función Sage que devuelve los divisores de “a”. |
||
#A partir de aquí podemos utilizar la potencia de Sage para encontrar las raíces a la ecuación, derivarla, integrarla, etc. La ecuación a*x**2+b*x+c==0 es la forma Python de representar nuestra ecuación, en el ejemplo 24x2 -120x + 144.
[…]
print es la orden que muestra por pantalla información: print(“Los divisores de “ + str(a) + “ son “ + str(divisors(a)).
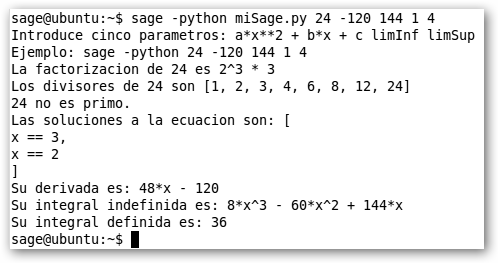
Observa el resultado de la salida en la figura de la derecha, prueba con otros argumentos.
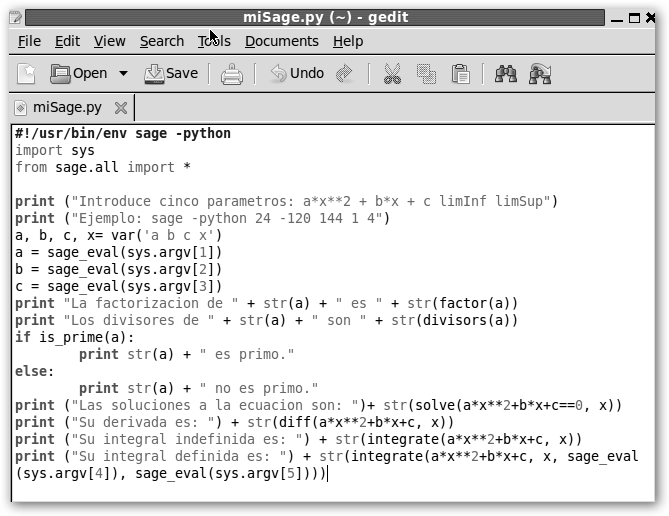
Se muestra en la
figura adjunta el código completo. Considera que con la
potencia de Sage tus programas escritos en Python pueden hacer
casi cualquier cosa, el límite son las estrellas
 . Este libro no pretende ser una
introducción a Python, puedes encontrar mucha más información
sobre este potente y moderno lenguaje en ¡Programa en GNU/Linux! de
esta misma editorial, así como, otro ejemplo de integración
con Sage donde se resuelven sistemas de ecuaciones.
. Este libro no pretende ser una
introducción a Python, puedes encontrar mucha más información
sobre este potente y moderno lenguaje en ¡Programa en GNU/Linux! de
esta misma editorial, así como, otro ejemplo de integración
con Sage donde se resuelven sistemas de ecuaciones.
12.2. ¡Sin límites! Implementación y representación gráfica del teorema de Bolzano.
Recuerda: Si f es
una función continua en el intervalo [a, b], f(a) y f(b)
tienen signos contrarios entonces el teorema de Bolzano establece que
existirá un punto intermedio c donde f(c)=0. ¡Tampoco se
mató el tipo ese, ni que fuera el “súper”
primo de Rajoy
 ¡Tú sí
que eres mi héroe!
¡Tú sí
que eres mi héroe!
Veamos un código Python (crea un fichero puntoMedio.py) donde vamos a encontrar las raíces de funciones, así como, vamos a mostrar gráficamente nuestro resultado.
import numpy
import pylab
from scipy.optimize import fsolve
#importamos las librerías necesarias
def bolzanoAux(a, b, f, limiteBusqueda):
puntoMedio = (a + b) / 2.0
if f(puntoMedio)==0 or b - a < limiteBusqueda:
#Si puntoMedio es raíz o b – a < limiteBusqueda hemos acabado
return puntoMedio
elif f(b)*f(puntoMedio) > 0:
# En otro caso, si f(b) y f(puntoMedio) tienen el mismo signo, la búsqueda continúa entre a y puntoMedio
return bolzanoAux(a, puntoMedio, f, limiteBusqueda)
else:
# Este último caso implica que f(b) y f(puntoMedio) tienen distinto signo, la búsqueda continúa entre puntoMedio y b
return bolzanoAux(puntoMedio, b, f, limiteBusqueda)
def bolzano(a, b, f, limiteBusqueda):
"""
Calcula la raíz basándose en el teorema de Bolzano.
Si la función f es continua en el intervalo [a, b], f(a) y f(b) tienen signos opuestos: f(a)*f(b)<0, entonces su raíz estará en un valor intermedio.
limiteBusqueda es el criterio de parada para no llegar a una computación infinita
"""
# Nuestra función tiene cuatro parámetros a, b, f, la función y un limiteBusqueda
if f(a)*f(b)>=0 or a >= b:
return "Error"
# Si f(a)*f(b)>=0 implica o bien que a y/o b son raíces o que tienen el mismo signo.
# El intervalo [a, b] necesita que a<b. Otra posible implementación sería intercambiarlos si observamos esta situación.
rangox = pylab.arange(a, b, 0.01)
rangoy = []
for x in rangox:
rangoy.append(f(x))
# Para dibujar la gráfica de la función necesitamos los puntos a graficar. En rangox están los puntos empezando en a, incrementándolos un 0.01 hasta b. Por cada uno de estos puntos (for x in rangox: ,es decir, en la variable x se almacenará todos estos puntos uno a uno por cada iteración del bucle), se evalúa la función (f(x)) y se añade a rangoy (rangoy.append(f(x)). Por tanto, ya tenemos todos los valores para dibujar f.
pylab.plot(rangox, rangoy, 'b')
# Dibujamos la función f
pylab.xlabel("Eje x")
pylab.ylabel("Eje y")
puntoMedio = bolzanoAux(a, b, f, limiteBusqueda)
# Dibujamos etiquetas en los ejes “x” e “y” y calculamos el punto medio
pylab.plot(puntoMedio, f(puntoMedio),'o', markersize=5)
# Dibujamos el punto medio que hemos encontrado con un circulo de un grosor mayor.
pylab.show()
# Mostramos la gráfica
print "Solución encontrada por scypy: " + str(fsolve(f,a))
# Utilizamos la función fsolve de ScyPy para resolver el mismo problema y comparar resultados.
return puntoMedio
# Devolvemos nuestra solución
def miFuncion(x):
return x-3
def miOtraFuncion(x):
return (x-2)*(x-5)
# Creamos dos funciones para comprobar nuestro código
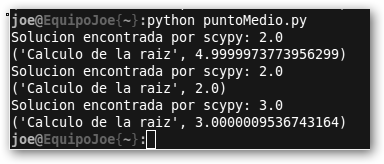
print("Calculo de la raíz", bolzano(2.25, 6, miOtraFuncion, 1e-5))
print("Calculo de la raíz", bolzano(1, 3, miOtraFuncion, 1e-5))
print("Calculo de la raíz", bolzano(1, 4, miFuncion, 1e-5))
# Realizamos varias llamadas a nuestra función bolzano.
|
Implementaciones ligeramente distintas del teorema de Bolzano puedes encontrar también en el más que recomendable “Introducción a la programación con Python” de Marzal y Gracia y en es.wikipedia.org/wiki/ Método_de_bisección. Prueba otras funciones como… import math |
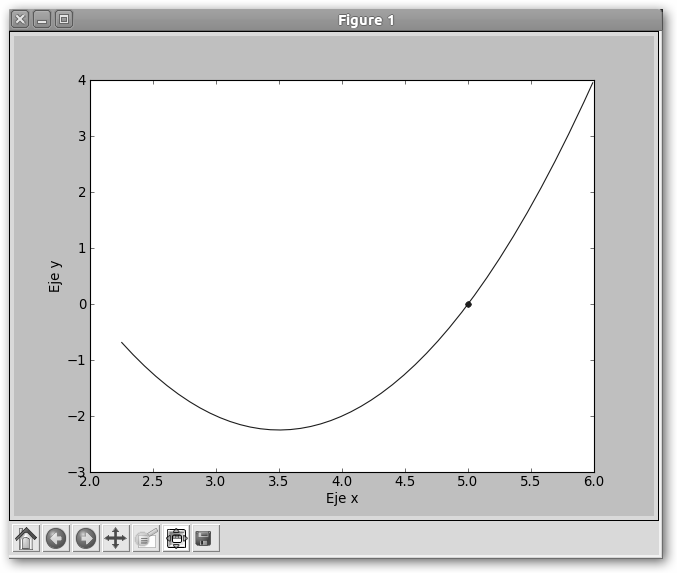
Comprueba el resultado obtenido: la representación gráfica de la función con el punto encontrado resultado y comprueba las diferencias con lo que devuelve ScyPy.
|
def miFuncion(x):
return (math.exp(x)*x) ó
return(math.atan(x)-1)
… y cambia los valores a y b convenientemente.
12.3. Dibujando en Python con coordenadas cartesianas, polares y paramétricas, así como, tartas, diagramas de barras y superficies 3D.
|
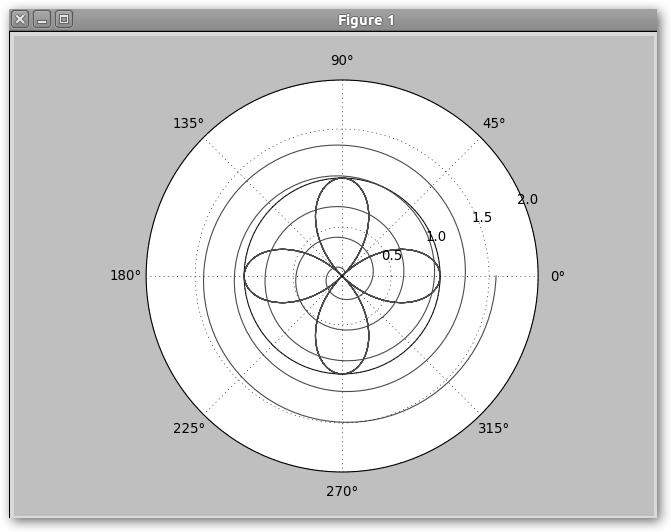
Empecemos dibujando en polares: from pylab import * theta = linspace(0,2*pi,1000) #Mi argumento theta será un array de 1000 elementos en el intervalo [0, 2Π] r = linspace(1, 1, 1000) #La distancia “r” es también un array de 1000 “unos”. polar(theta,r) theta = linspace(0, 2*pi,1000) r = cos(2*theta) polar(theta,r) theta = linspace(0, 10*pi,1000) r = 0.05*theta polar(theta,r) show() # Muestra los tres gráficos. |
polar(theta, r) es la función que nos permite dibujar en polares. Se le pasa como argumentos sendos arrays de argumentos y distancias. En el primer caso, r=1, theta variando en [0, 2Π] dibujamos un círculo de radio 1. En el segundo caso: r=cos(2*theta) con theta en [0, 2Π] dibujamos una rosa polar. Modifica 2 para formar rosas con distintos número de pétalos. Finalmente, dibujamos una espiral de Arquímedes: r=0.05*theta con theta en [0, 10 Π]. Recuerda escribir este código en un fichero con extensión .py (p.e. polares.py) e invocarlo desde consola. |
|
|
¿Quién dijo que no le gustaban las mates y que no podían ser chulas? Observa los gráficos que hemos obtenido con el siguiente código: |
||
|
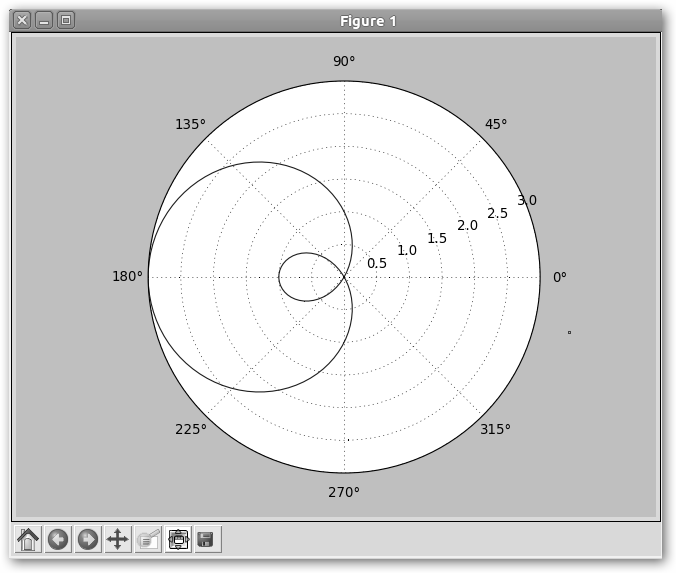
from pylab import * theta = linspace(-pi, pi, 10000) r=1-2*cos(theta) polar(theta,r) show() |
Resultado del código anterior: r=1-2*cos(theta) y theta oscilando en [-Π, Π] |
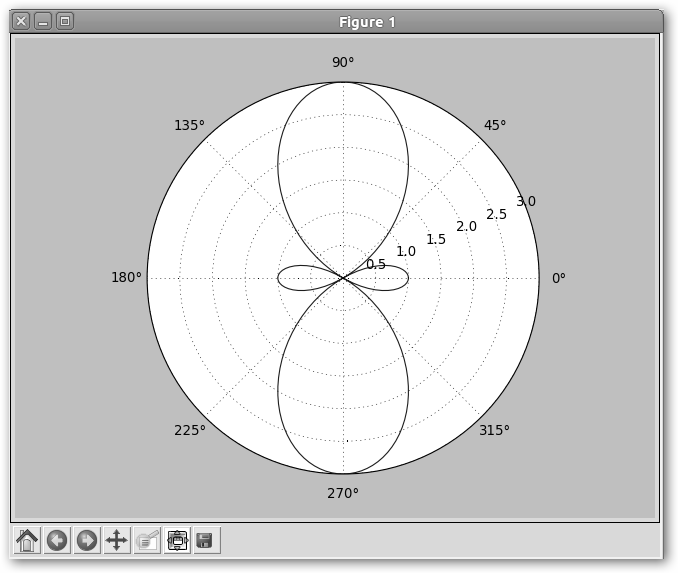
Sólo hemos cambiado un humilde “2” y contrasta la diferencia: r=1-2*cos(2*theta). |
|
Dibujamos ahora en paramétricas (x=función1(t), y=función2(t)) con plot(x,y): |
||
|
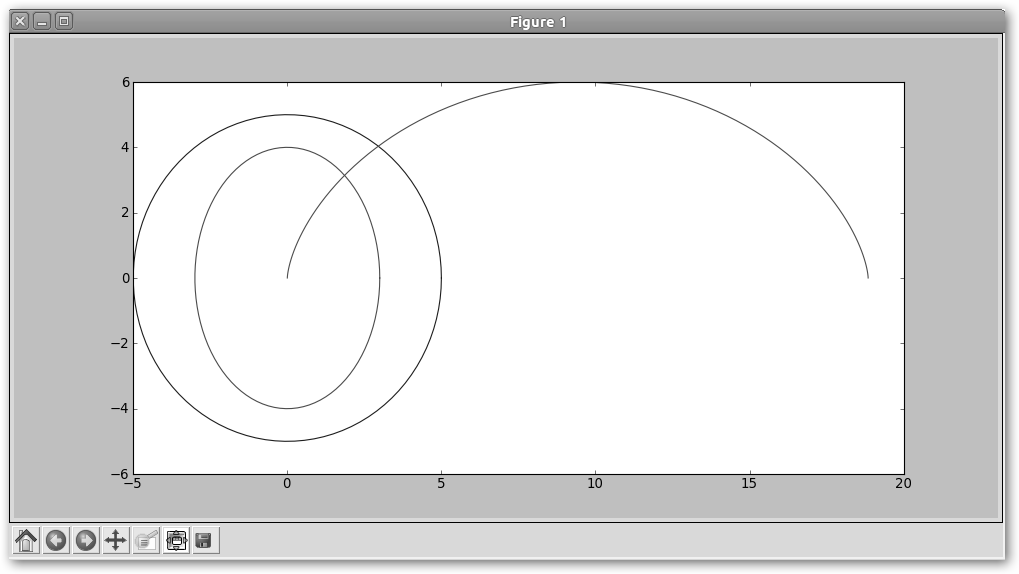
from pylab import * radio = 5.0 t = linspace(0, 2*pi, 100) x = radio * cos(t) y = radio * sin(t) plot(x,y) radio1 = 3 radio2 = 4 x = radio1 * cos(t) y = radio2 * sin(t) plot(x,y) radio = 3 x = radio * (t - sin(t)) y = radio * (1 - cos(t)) plot(x,y) show() |
Comprueba lo obtenido: 1. Círculo de radio 5: x = radio*cos(t), y = radio*sin(t) con theta oscilando entre [0, 2Π]. 2. Elipse: x = radio1*cos(t), y = radio2*sin(t) con theta variando en el mismo intervalo. 3. Cicloide: x = radio*(t-sin(t)), y=radio*(1-cos(t)). |
|
|
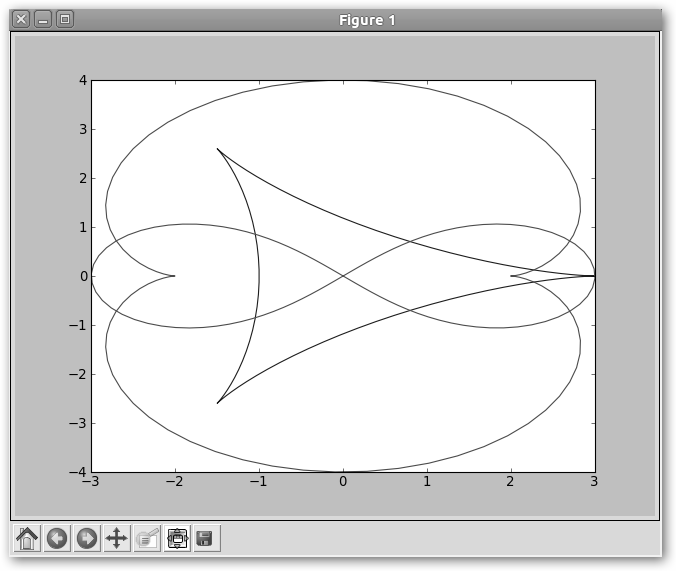
Veamos otro ejemplo: from pylab import * t = linspace(0, 2*pi, 100) x = 2*cos(t)+cos(2*t) y = 2*sin(t)-sin(2*t) plot(x,y) x = 3*cos(t)-cos(3*t) y = 4*(sin(t)**3) plot(x,y) x=3*sin(t)/(1+cos(t)**2) y=3*sin(t)*cos(t)/(1+cos(t)**2) plot(x,y) show() |
Hemos dibujado tres curvas famosas: Deltoide, Nefroide y Lemniscata de Bernoulli. |
|
|
Se muestra como dibujar en cartesianas pero como puedes comprobar no hay nada nuevo bajo el sol. from pylab import * x = linspace(-2*pi, 2*pi , 1000) x3 = linspace(0.0001, 2*pi , 1000) y1 = sin(x) y2 = cos(x) y3 = sin(2*x)+3*cos(x) |
||
|
plot(x,y1) plot(x,y2) plot(x,y3) show() |
|
|
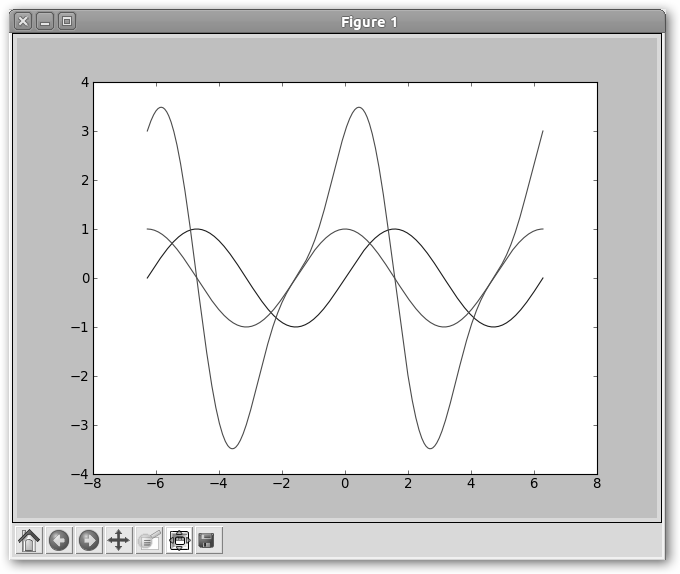
|
Resultado del código anterior, se ilustran las funciones seno, coseno y seno(2x)+3coseno(x). Otra cosa bien diferente es dibujar en 3D. |
||
|
from pylab import * from mpl_toolkits.mplot3d import Axes3D import numpy figura = Axes3D(figure()) x = arange(-2, 2, 0.1) y = arange(-2, 2, 0.1) xx, yy = meshgrid(x, y) aux = -(xx**2 + yy**2) z = numpy.exp(aux) figura.plot_surface(xx, yy, z, cmap=cm.jet, rstride=1, cstride=1) show() |
|
|
|
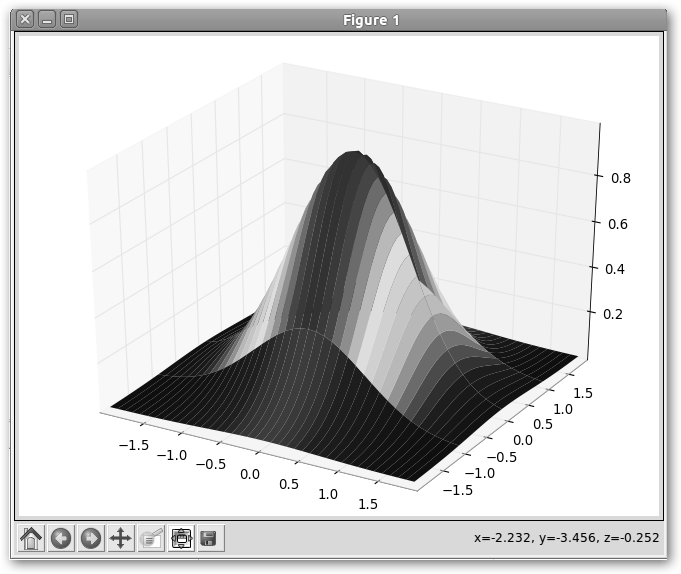
Veamos las instrucciones clave: 1. Creamos dos rejillas, matrices o mallas con los vectores x e y: xx, yy = meshgrid(x, y). Por ejemplo, si x = arange(2, 8, 2) e y = arange(1, 7, 2) obtendríamos que “xx” sería array([[2, 4, 6], [2, 4, 6], [2, 4, 6]]) e “yy” array([[1, 1, 1],[3, 3, 3], [5, 5, 5]]). 2. Definimos nuestra función
en dos cómodos plazos
3. Creamos un objeto Axes3D: figura = Axes3D(figure()) 4. Graficamos en 3D utilizando el método plot_surface del objeto figura de la clase Axes3D: figura.plot_surface(xx, yy, z, cmap=cm.jet, rstride=1, cstride=1). Los parámetros más importantes son: las mallas obtenidas previamente con meshgrid; los valores de la función 3D en dichas mallas (z=f(xx, yy)); y cmap=cm.jet que define un mapa de conversión de colores, es en realidad una instancia de matplotlib.cm.ColorMap, por ejemplo, cm.jet. 5. Mostramos la gráfica: show(). Python puede con todo, mostramos para finalizar como dibujar diagramas de tartas y de barras. |
||
|
|
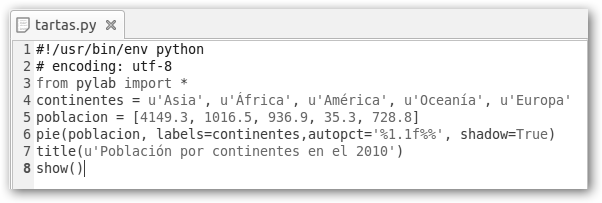
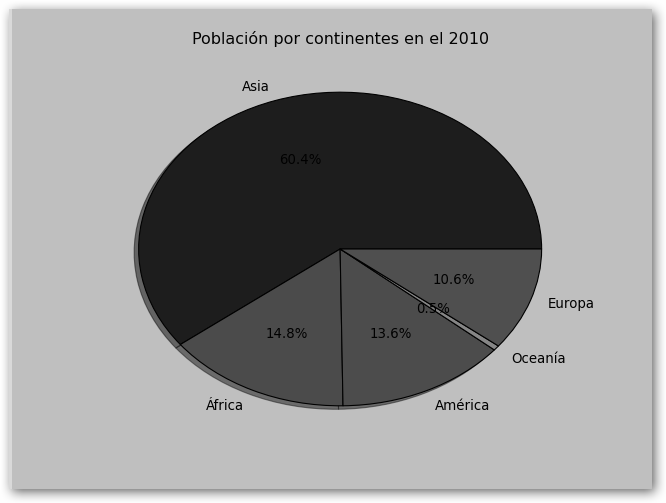
La instrucción fundamental es pie a la que se le pasan como argumentos: el array de valores a graficar (poblacion “sin tilde”), las etiquetas (labels=continentes), autopct con el que mostramos los porcentajes en los quesitos y shadow=True para que dibuje una sombra debajo de la tarta. |
|
|
Fíjate en las líneas 1, 2, 4 y 7, estamos utilizando Unicode para poder mostrar las tildes. #!/usr/bin/env python # encoding: utf-8 from pylab import * from numpy import * from matplotlib import * |
|
|
|
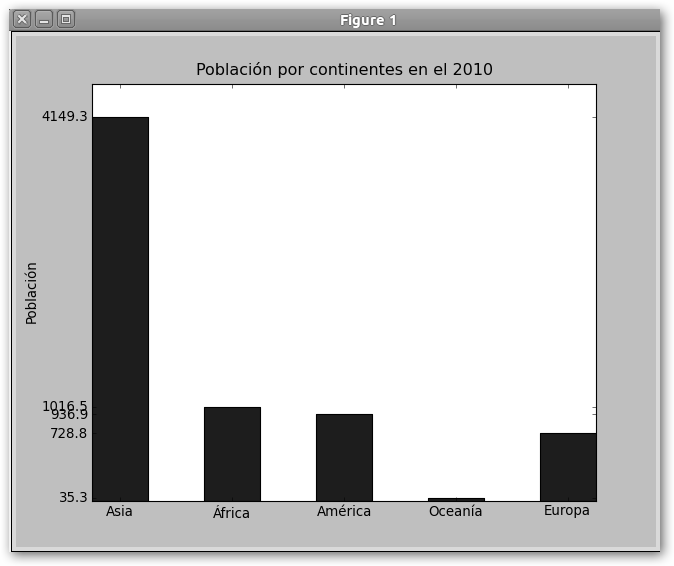
continentes = u'Asia', u'África', u'América', u'Oceanía', 'Europa' poblacion = [4149.3, 1016.5, 936.9, 35.3, 728.8] coordenadas = arange(5) anchoBarras = 0.5 pyplot.bar(coordenadas, poblacion, anchoBarras, color='b') pyplot.ylabel(u'Población') pyplot.title(u'Población por continentes en el 2010') pyplot.xticks(coordenadas+anchoBarras/2., continentes) #Escribiremos Asia en anchoBarras/2, África en 1+anchoBarras/2,… pyplot.yticks(poblacion) pyplot.show() |
||
|
La orden a tener en cuenta es pyplot.bar(coordenadas, poblacion, anchoBarras, color='b'). A bar se le pasan los siguientes argumentos: coordenadas “x” –límite inferior- de las barras (coordenadas = arange(5) = [0 1 2 3 4]); alturas “y” de las barras (población), ancho de las barras (anchoBarras) y el color (azul). |
|
|
12.4. Visual Python, animaciones y geometría en 3D.
Visual Python es una librería de Python que nos permite realizar geometría en tres dimensiones. Su portal Web es http://vpython.org/ y desde él podrás descargar este paquete. ¡Funciona sólo con Python 2.7! Por tanto, instálalo en el directorio de Python 2.7 y arranca el correspondiente IDLE. En Windows sería: Inicio, Todos los programas, Python 2.7, IDLE (Python GUI). Teclea un archivo, digamos MyVisual.py, en el directorio Lib de Python 2.7 con el siguiente contenido:
from visual import *
p = pyramid(pos=(5,2,0), size=(12,6,4), color = color.yellow)
b = box(pos=(0,0,0), size=(2, 2, 2), color = color.red)
s = sphere()
s.radius=3
x = 0
while 1:
|
p.pos=[0, 5*cos(x),5*sin(x)] s.pos=[0, 3*sin(x),3*cos(x)] x = x + .1 rate(2) |
|
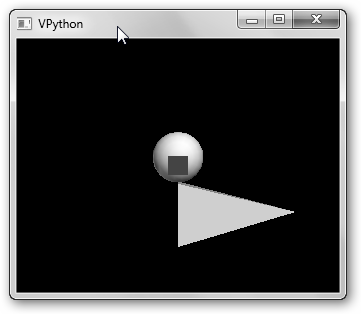
No es pretensión de este título explicar extensamente VPython, solo comentarte algunas líneas de código para que puedas ponerte ya manos a la obra. En su portal web encontrarás bastante documentación e incluso algunos vídeos introductorios.
* from visual import *: importamos la librería VPython.
* p = pyramid(pos=(5,2,0), size=(12,6,4), color = color.yellow): p es un objeto pirámide en una determinada posición en el espacio (el centro de la base rectangular se especifica por pos) con un determinado tamaño (size, la base tiene como dimensiones 6 y 4 y la longitud entre la base y la cúspide es 12) y de color amarillo.
* b = box(pos=(0,0,0), size=(2, 2, 2), color = color.red): b es un cubo, al constructor (el método que crea el objeto) se le han pasado tres argumentos para definir, de forma completamente análoga a la instrucción anterior, su posición, tamaño y color.
* s = sphere(): creamos una esfera. También, tenemos a nuestra disposición otros cuerpos geométricos, a saber: cilindros, anillos, flechas, conos, etiquetas, escenarios, etc.
* s.radius=3: ilustra cómo podemos modificar los atributos de los objetos geométricos recién creados, en este caso, el radio de la esfera. Podríamos cambiar otras propiedades de la esfera, por ejemplo, el material y el color: s.materials = materials.earth, s.color = color.blue.
A continuación, ejecutamos un bucle infinito (while(1)) para realizar una animación (al variar x con x = x + .1) donde rotamos tanto la pirámide (p.pos=[0, 5*cos(x),5*sin(x)]) como la esfera (s.pos=[0,3*sin(x),3*cos(x)]) sobre el eje X. Un último detalle: rate(2) “ralentiza” la animación y permite observar que está pasando.
12.5. Introducción a la Programación Orientada a Objetos
Para entender la programación orientada a objetos debemos conocer los conceptos de clases y objetos. Una clase es un “modelo”, una plantilla que define las características de todos los objetos o instancias de la clase. Por ejemplo, podríamos tener las clases Triángulo, Cuadrado, Polígono, etc. Un objeto sería una instancia u ocurrencia particular de la clase, por ejemplo, un objeto Triángulo tendría una determinada base y altura. ¿A que nos referimos con las características que se definen en la clase? Básicamente a:
* Atributos: son las propiedades, variables o características individuales.
* Métodos: definen su comportamiento, la interfaz con el resto del mundo.
class Triangulo:
"""Esta clase representa el concepto geométrico de Triángulo.
"""
def__init__(self, b, h):
"""Constructor con dos argumentos: base y altura."""
self.b = b
self.h = h
def area(self):
"""Devuelve el área del triángulo."""
return self.b*self.h/2
if __name__ == '__main__':
t = Triangulo(5, 2)
help(t)
print t.area()
Definimos nuestra primera clase, la clase Triángulo.
1. Nuestra clase Triángulo tiene dos métodos: un constructor, __init__ con dos guiones bajos (“__”) antes y después de init y área. Cuando en el cuerpo del programa, creamos una instancia u objeto de la clase Triangulo “t” (t=Triangulo(5, 2)), llamamos precisamente al constructor.
2. El constructor define dos atributos o variables: b y h que son la base y la altura del triángulo respectivamente. En el constructor estos atributos se inicializan con los dos argumentos que recibe, en el ejemplo, la base del objeto “t” (“b”) es 5 y la altura (“h”) 2.

3. Observa que todos los métodos tienen como primer argumento self, el objeto en sí. Sin embargo, al invocar estos métodos desde los objetos este argumento se omite, Python lo añadirá por nosotros.
4. Después de crear el objeto Triángulo, invocamos al método área. Éste simplemente devuelve el producto de la base y la altura dividido por dos, en el ejemplo 5*2/2=5.
5. Considera también que hemos documentado el código. En Python todos los objetos cuentan con una variable __doc__ que puede definirse como la cadena de documentación que nos sirve para hacer legible nuestro código. Observa que inmediatamente después de la definición de la clase introducimos el comentario: """Esta clase representa el concepto geométrico de Triángulo.""", así como, después de la definición de cada método. Python actualizará por nosotros la variable __doc__ que podrá ser consultada con help(t).
12.6. Herencia en Python: “P.O.O a toda potencia”.
La programación orientada a objetos es interesante porque nos permite programar de una forma más cercana al mundo real donde encontramos objetos (lavadoras, coches, ordenadores, etc.) con determinadas propiedades (capacidad de carga –lavadora-, matrícula -coche-, memoria RAM, velocidad de la CPU –ordenador-, etc.) y con una determinada funcionalidad (cargar la lavadora, centrifugar, arrancar el vehículo, encender el ordenador, ejecutar un programa,etc.).
Sin embargo, la programación orientada a objetos alcanza todo su esplendor y potencia cuando utilizamos la herencia. Pero,… ¿qué es la herencia? Es el mecanismo por el cual una clase, que llamaremos clase derivadapuede heredar de otra sus atributos y métodos, así como, añadir nuevos para extender, ampliar o modificar el comportamiento de la clase padre o base.
# -*- coding: cp1252 -*-
miLista1 = [1, 2, 3, 4, 1, 5, 1, 6]
class MiConjunto(set):
"""Esta clase representa una extensión de los conjuntos de Python."""
def__init__(self, lista):
"""Constructor, toma como argumento una lista de elementos,
no necesariamente distintos"""
set.__init__(self, lista)
def cardinalidad(self):
"""Devuelve el número de elementos del conjunto."""
return len(self)
if__name__ == '__main__':
a = MiConjunto(miLista1)
print "Cardinalidad de ", a, " es ", str(a.cardinalidad())
Observa que la clase padre es “set”, que es la clase que implementa en Python los conjuntos. Luego, la clase derivada MiConjunto tiene como clase base “set”.
Fíjate que en el constructor hacemos una invocación al constructor de la clase padre: set.__init__(self, lista).
Hemos añadido un nuevo método denominado cardinalidad.
¡Ojo!, cuando creamos una instancia de MiConjunto “a”, el argumento es la lista “miLista1” que tiene elementos repetidos.
El resultado por consola es el siguiente: Cardinalidad de MiConjunto([1, 2, 3, 4, 5, 6]) es 6.
12.7. Programación funcional en Python.
Matemáticamente, Python tiene muchas ventajas: pequeña curva de aprendizaje, la cantidad de librerías matemáticas y gráficas que incluye, legibilidad de su código, etc. Sin embargo, otro elemento que debemos descubrir y ponderar en su justa medida es que podemos programar en Python con el paradigma funcional, es decir, desde una perspectiva muy cercana a como pensamos matemáticamente un problema.
# -*- coding: cp1252 -*-
from string import *
miLista1 = [1, 2, 3, 4, 1, 5, 1, 6]
miLista2 = [1, 2, 3, 4, 8]
listaCastellana = ["chicha", "video", "meollo", "pera", "paella", "siesta"]
listaInglesa = ["song", "music", "help", "siesta", "video", "run"]
Veamos el código del programa anterior bastante ampliadito.
Vamos a utilizar tanto listas de números como de cadenas de caracteres para demostrar que nuestro conjunto representa el concepto general matemático.
El principio del código de la clase MiConjunto es exactamente igual al apartado anterior.
class MiConjunto(set):
"""Esta clase representa una extensión de los conjuntos de Python."""
def __init__(self, lista):
"""Constructor, toma como argumento una lista de elementos, no necesariamente distintos"""
set.__init__(self, lista)
def cardinalidad(self):
"""Devuelve el número de elementos del conjunto."""
return len(self)
def interseccion(self, otroConjunto):
"""Retorna la intersección con otroConjunto"""
return MiConjunto([e for e in self if e in otroConjunto])
La intersección de dos conjuntos la hemos obtenido con: return MiConjunto([e for e in self if e in otroConjunto]); en un estilo “funcional”, se podría leer como: “la intersección es el conjunto de mis elementos que también pertenecen a otroConjunto”. El propósito de esta implementación es instructivo, se podría haber utilizado el método padre de set “&”: return self & otroConjunto.
def __sub__(self, otroConjunto):
"""Devuelve la diferencia self - otroConjunto"""
return MiConjunto([e for e in self if e not in otroConjunto])
def diferenciaSimetrica(self, otroConjunto):
"""Devuelve la diferencia simétrica de self y otroConjunto"""
return (self-otroConjunto)|(otroConjunto-self)
Podríamos habernos ahorrado definir el método diferencia A-B, porque ya estaba implementado en la clase padre set. El propósito pedagógico de este método es comprobar otra característica de la P.O.O.: el polimorfismo. Redefiniendo con __sub__ la resta, permitimos utilizar nuestra clase al usuario como él está acostumbrado con el operador “-“: a-b, c-d, etc.
La diferencia simétrica A∆B podría haberse implementado con el código return self^otroConjunto o haber utilizado directamente el operador “^” ya sobrecargado por “set” para definir A∆B como A^B.
def __add__(self, otroConjunto):
"""Unión con otroConjunto"""
return self | otroConjunto
def pertenece(self, elemento):
"""Indica si elemento pertenece al conjunto."""
if elemento in self:
return str(elemento)+" pertenece a "+str(self)
else:
return str(elemento)+" no pertenece a "+str(self)
def funcion(self, f):
"""Devuelve el conjunto resultante de aplicar f a todos los elementos del conjunto."""
return map(f, self)
def filtra(self, f):
"""Retorna el conjunto resultante de filtrar por f los elementos del conjunto."""
return MiConjunto(filter(f, self))
def miReduce(self, f):
"""Devuelve el elemento resultante de reducir por f nuestro conjunto."""
return reduce(f, self)
Más interesante aún son las tres funciones siguientes: función, filtra, miReduce. En ellas se utiliza tres funciones clásicas de la programación funcional, a saber:
1. map, tiene dos argumentos: una función y una secuencia (lista, conjunto,…). Devuelve el conjunto resultante de aplicar f sobre cada uno de los elementos del conjunto original, es decir, {f(e), e ε C }.
2. filter: con los mismos argumentos que map devuelve un conjunto con todos aquellos elementos del conjunto original que satisfacen que la función en ellos es True, verdadero: {e: e ε C y f(e)=True}.
3. reduce: devuelve un único valor. Para obtenerlo, primero aplica f sobre el primer y el segundo elemento del conjunto; luego, aplica f sobre el resultado y el tercer elemento y así sucesivamente.
def claseEquivalencia(self, elemento, r):
"""Obtiene la clase de equivalencia de <<elemento>> con la relación <<r>>."""
return MiConjunto([e for e in self if r(e, elemento)])
class ConjuntoCociente:
"""Esta clase representa el concepto matemático de Conjunto Cociente."""
def __init__(self, conjunto, r):
"""Los argumentos son: el conjunto y la relación r de equivalencia."""
self.elementos = MiConjunto([])
self.miLista = []
for e in conjunto:
if e not in self.elementos:
self.miLista.append( conjunto.claseEquivalencia(e, r))
self.elementos += conjunto.claseEquivalencia(e, r)
def __str__(self):
"""Imprimo convenientemente la clase de equivalencia."""
return ' '.join([str(e) for e in self.miLista])
if __name__ == '__main__':
a = MiConjunto(miLista1)
b = MiConjunto(miLista2)
c = MiConjunto(listaCastellana)
d = MiConjunto(listaInglesa)
print "Cardinalidad de ", a, " es ", str(a.cardinalidad())
print "Cardinalidad de ", c, " es ", str(c.cardinalidad())
print "Interseccion de conjuntos: ", a.interseccion(b)
print "Interseccion de conjuntos: ", c.interseccion(d)
print "Diferencia de ", a, " y ", b, " es ", a-b
print "Diferencia de ", c, " y ", d, " es ", c-d
print "Diferencia simétrica de ", a, " y ", b, " es ", a.diferenciaSimetrica(b)
print "Diferencia simétrica de ", c, " y ", d, " es ", c.diferenciaSimetrica(d)
print "La unión de ", a, " y ", b, " es ", a+b
print "La unión de ", c, " y ", d, " es ", c+d
print "¿está el tres en mi conjunto? " + a.pertenece(3)
print "¿está file en mi conjunto? " + c.pertenece("file")
print "Aplico x**2 a ", a, " es ", a.funcion(lambda x: x**2)
print "Aplico convertir a mayúsculas a ", c, " es ", c.funcion(upper)
print "Filtro los impares a ", a, " y resulta en ", a.filtra(lambda x: x % 2 == 0)
print "Filtro las palabras cortas en ", c, " y resulta en ", c.filtra(lambda x: len(x)>5)
print "Sumo todos los números del conjunto ", a, " es " + str(a.miReduce(lambda x, y: x + y))
print "Clase de equivalencia del 1 ", a.claseEquivalencia(1, lambda x, y: (x -y) % 3 == 0)
print "Clase de equivalencia del 2 ", a.claseEquivalencia(2, lambda x, y: (x -y) % 3 == 0)
print "Clase de equivalencia del 3 ", a.claseEquivalencia(3, lambda x, y: (x -y) % 3 == 0)
print "Clase de equivalencia de pera ", c.claseEquivalencia("pera", lambda x, y: len(x)==len(y))
print "Clase de equivalencia de meollo ", c.claseEquivalencia("meollo", lambda x, y: len(x)==len(y))
print "Conjunto cociente", ConjuntoCociente(a, lambda x, y: (x -y) % 3 == 0)
print "Conjunto cociente", ConjuntoCociente(a, lambda x, y: (x -y) % 2 == 0)
print "Conjunto cociente", ConjuntoCociente(a, lambda x, y: x == y)
print "Conjunto cociente", ConjuntoCociente(c, lambda x, y: len(x)==len(y))
¿Y cómo calculamos la clase de equivalencia de un elemento? Con una sola línea: return MiConjunto([e for e in self if r(e, elemento)]), es decir, todos mis elementos que estén relacionados con el elemento dado. ¡Considera el nivel de abstracción!, f y r son “cualquier” función y relación de equivalencia respectivamente sobre “cualquier” conjunto.
¿Cómo creamos el conjunto cociente? Con una nueva clase denominada ConjuntoCociente (¿soy original, eh?). En el atributo “miLista” guardo todas las clases de equivalencia y en “elementos” todos los elementos del conjunto dado como argumento conforme los voy considerando.
El constructor tiene como argumentos tanto el conjunto como la relación de equivalencia obviamente. Itero sobre el conjunto (for e in conjunto:), así “e” sería uno de sus elementos y añado su clase de equivalencia (self.miLista.append( conjunto.claseEquivalencia(e, r)))
siempre y cuando no lo haya ya considerado (if e not in self.elementos). Si no lo había contado todavía también añado dicho elemento y todos los de su clase de equivalencia a self.elementos
Considera que se emplean bastantes funciones anónimas o funciones lambda para escribir menos código y observa el resultado final en la ilustración inferior.
Nuestra clase ConjuntoCociente puede utilizarse en la relación de equivalencia (x-y) % 3 ==0 sobre enteros, así como, len(x)==len(y) sobre cadenas. En el primer caso, obtenemos: {{1, 4}, {2, 5}, {3, 6}}; en el segundo, el resultado es: {{pera}, {meollo, chicha, paella, siesta}, {video}}.
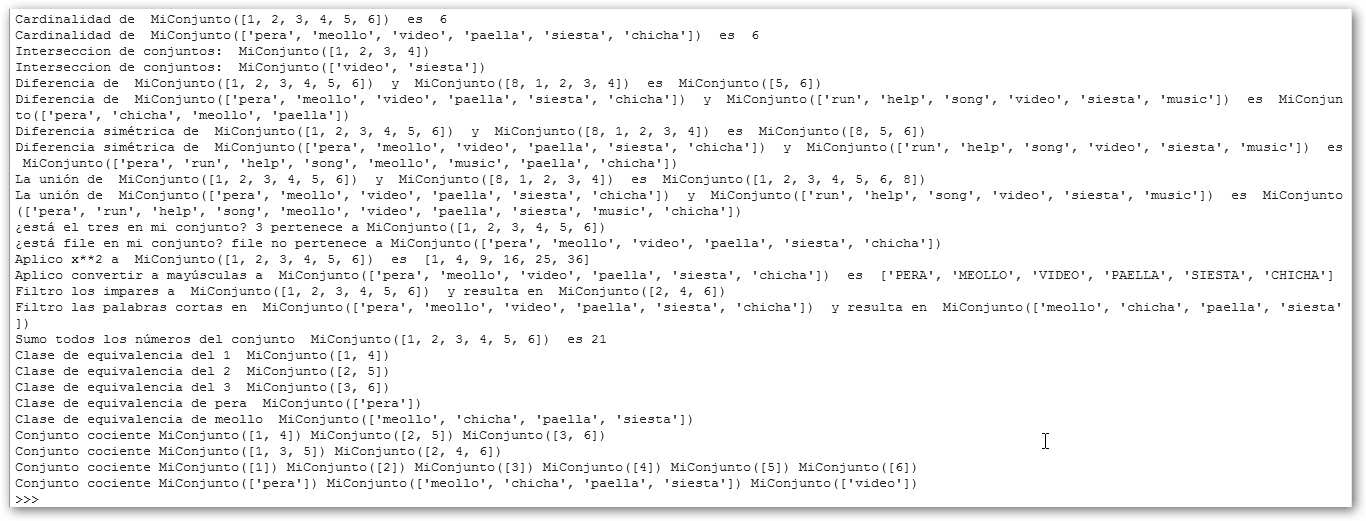
¿Y si solicitamos: print "Conjunto cociente", ConjuntoCociente(c, lambda x, y: x[0]==y[0])? Efectivamente, recuperamos el conjunto cociente de la relación de equivalencia de las palabras que empiezan por la misma letra: Conjunto cociente MiConjunto(['pera', 'paella']) MiConjunto(['meollo']) MiConjunto(['video']) MiConjunto(['siesta']) MiConjunto(['chicha']).
Finalmente, observa que también podemos obtener la relación de equivalencia “x” R “y” sii (si y solo si) area(x)==area(y) sobre un conjunto de triángulos (dos triángulos están relacionados si poseen el mismo área):
listaTriangulos = [Triangulo(5, 2), Triangulo(2, 5), Triangulo(6, 4),Triangulo(3, 8), Triangulo(4, 6), Triangulo(12, 2)]
e = MiConjunto(listaTriangulos)
print "Conjunto cociente", ConjuntoCociente(e, lambda x, y: x.area()==y.area())
Previamente deberíamos definir cómo se mostrarán los triángulos:
class Triangulo:
"""Esta clase representa el concepto geométrico de Triángulo."""
[…]
def__str__(self):
return "Triángulo con base " + str(self.b) + " y altura " + str(self.h)
def __repr__(self):
return "Triángulo con base " + str(self.b) + " y altura " + str(self.h)
Y el resultado es: Conjunto cociente MiConjunto([Triángulo con base 2 y altura 5, Triángulo con base 5 y altura 2]) MiConjunto([Triángulo con base 6 y altura 4, Triángulo con base 12 y altura 2, Triángulo con base 4 y altura 6, Triángulo con base 3 y altura 8]).
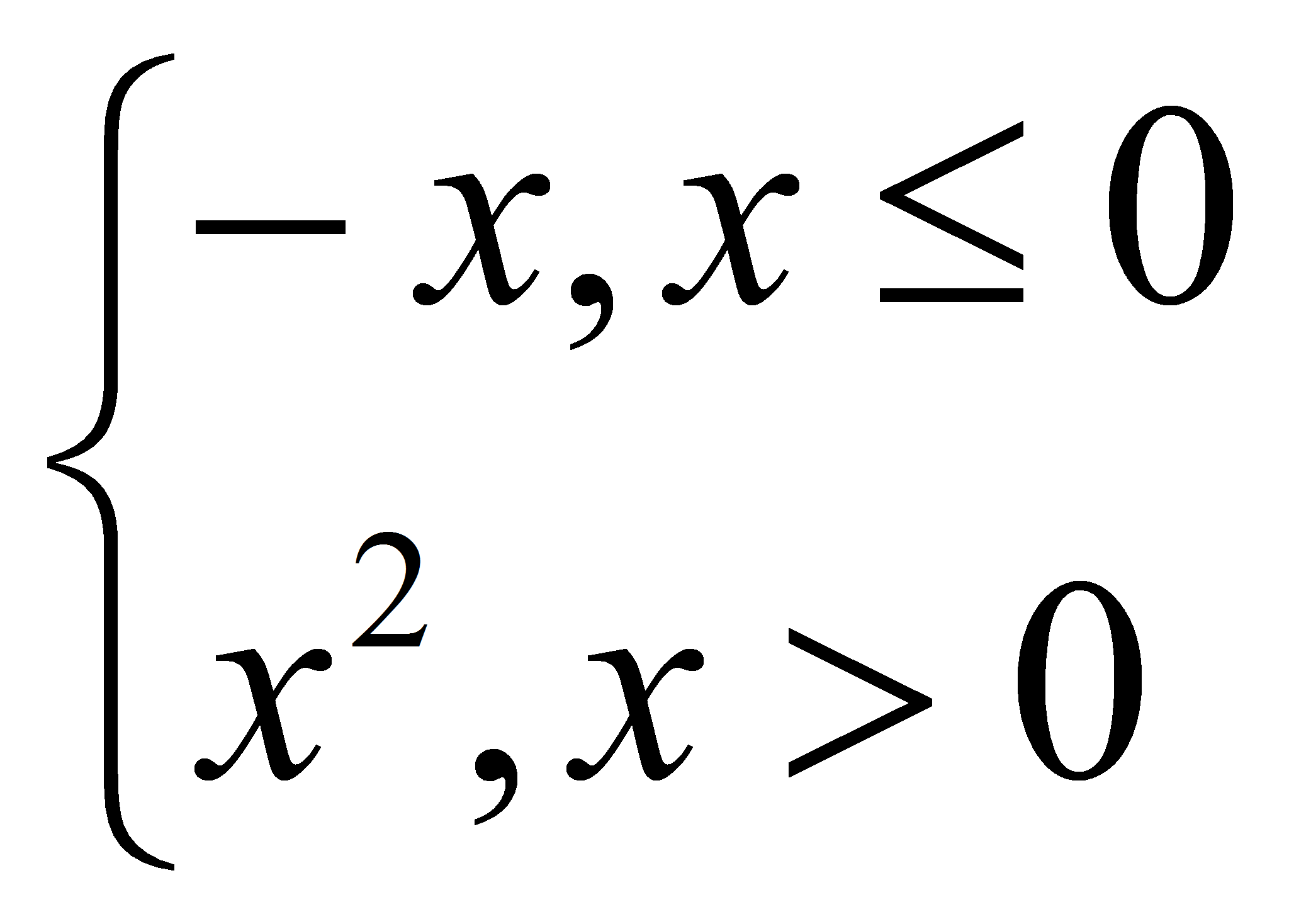 . Luego, la evaluamos en x=3, 3>0,
miFuncion(3)=9. Finalmente, la dibujamos utilizando el comando plot.
. Luego, la evaluamos en x=3, 3>0,
miFuncion(3)=9. Finalmente, la dibujamos utilizando el comando plot. : ¡podemos
utilizar la potencia de Sage desde nuestros
programas de Python! Veamos como:
: ¡podemos
utilizar la potencia de Sage desde nuestros
programas de Python! Veamos como: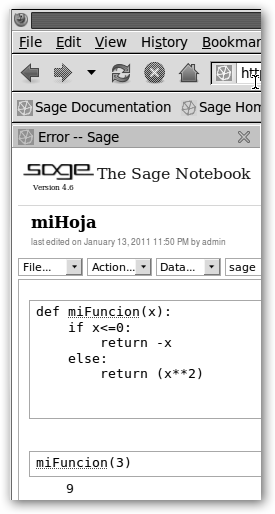
 , quiero decir pasos,
, quiero decir pasos,