11. Matemáticas con Python: a las serpientes les gustan las mates.
11.2. Primeros pasos con Python
11.3. Estructuras de control y funciones
11.4. Manejando ficheros y modos de trabajo con Python
11.5. La tortuga más “compleja”
11.6. Cálculo simbólico con SymPy
11.7. NumPy, SciPy y matplotlib: todos para uno, uno para todos
11.1. ¿Qué es Python?
Python es un lenguaje de programación moderno, libre, de propósito general, orientado a objetos, multiplataforma (funciona en Windows, GNU/Linux y MacOS). Puede ser utilizado con el paradigma de la programación de objetos en mente pero es también un lenguaje funcional y de script.
Es ideal para profundizar e investigar en las matemáticas por ser un lenguaje muy fácil de aprender. Parte de la culpa recae en que su código suele ser bastante legible. Para estudiarlo a fondo te aconsejamos el libro ¡Programa en GNU/Linux! de esta misma material. Otros lugares de obligado peregrinaje son: Dive Into Python (http://diveintopython.org/index.html), Learning To Program, (http://www.freenetpages.co.uk/hp/alan.gauld/), How to Think Like a Computer Scientist (http://openbookproject.net//thinkCSpy) y la documentación oficial (http://docs.python.org/).
11.2. Primeros pasos con Python.
Si utilizas GNU/Linux probablemente ya lo tengas instalado y si tu sistema operativo de preferencia es Windows descárgatelo desde www.python.org, en la sección Download, Python Windows Installer.
En Ubuntu basta con escribir en la consola (Aplicaciones, Accesorios, Terminal) python. En Windows navega por Inicio, Todos los programas, Python 3.1, IDLE. IDLE no es más que un IDE, un entorno de desarrollo para Python, para facilitar las tareas de programación al usuario, hacerle más productivo.
Existen
otros entornos de programación para Python, la mayoría
son multiplataforma: SPE (Editor de Python Stani,
pythonide.blogspot.com),
Boa Constructor (boa-constructor.sourceforge.net),
DrPython (drpython.sourceforge.net),
PIDA (pida.co.uk),
entre otros. Cabe ahora destacar también un intérprete
de Python mejorado para cómputo académico y científico,
IPython (ipython.scipy.org).
Aunque la página inicial es para llorar
 o para echarle pesetitas…, la herramienta bien merece la pena.
Otra distribución de Python orientado al entorno científico
es pythonxy (www.pythonxy.com).
o para echarle pesetitas…, la herramienta bien merece la pena.
Otra distribución de Python orientado al entorno científico
es pythonxy (www.pythonxy.com).
|
|
Python
puedes empezar a utilizarlo como una super calculadora como se
ilustra en la figura. ¡Pruébalo!
Teclea: 1/2+3/4, 3**2 (=32), 7%2 (7 módulo 2), … Sin embargo, es mucho más. Es un lenguaje de programación que entre sus tipos base está el complejo: type(3+2j) devuelve que pertenece a la clase complejo. Podemos realizar todas las operaciones básicas con ellos. Observa que hemos definido un complejo y accedido a su parte real e imaginaria. |
|
Prueba también de math: seno (p.e. math.sin (math.pi)), coseno (cos), tangente(tan), logaritmo (log), factorial, potencia (pow), etc. |
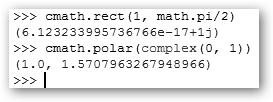
¡Python viene con las baterías cargadas! Al importar las librerías math (import math) y cmath añades múltiples funciones. Sirvan como primeros ejemplos: la raíz cuadrada de 9 y el argumento y el módulo de un número complejo: cmath.phase(complex(3,2)) devuelve el argumento y abs(complex(3, 2)) el módulo. |
|
Decimal es una librería que nos permite trabajar con números flotantes en la precisión que más nos convenga. Teclea por ejemplo: decimal.getcontext().prec = 3 (precisión 3) y decimal.Decimal(2).sqrt() (la raíz de 2) obtendrás Decimal('1.41'). |
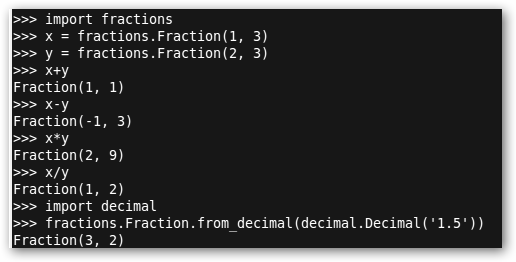
Las funciones rect y polar convierten un complejo a coordenadas cartesianas y polares respectivamente. Comprueba siempre el error, aunque es pequeñito, de redondeo. Obviamente las coordenadas cartesianas del complejo con módulo 1 y argumento Pi/2 es j. También podemos trabajar con fracciones importando la librería fractions (import fractions). Observa que al sumar dos fracciones, el resultado se ha simplificado (3/3=1/1). Además, podemos construir fracciones a partir de decimales (1.5); para ello creamos primero el decimal (decimal.Decimal(‘1.5’)) y se lo pasamos al método de Fraction from_decimal (requerimos la librería decimal). |
|
Centrándose en lo básico, Python consta pues de enteros (7), flotantes (5.0), largos (4L), complejos (3+2j), cadenas (p.e. “Me molan las mates”) y listas (miLista=[2, 4, 6, 8, 10]). La sintaxis de Python es muy minimalista, evitándose muchos signos de puntuación de los lenguajes de programación tradicionales (C/C++, Java, PHP, etc.) se consigue un lenguaje muy legible. El inconveniente es que tienes que tener mucho cuidado a la hora de tabular. Para salir escribe quit() y para obtener ayuda dispones de help(), una ayuda interactiva o help(orden), por ejemplo, help(len). |
|
|
|
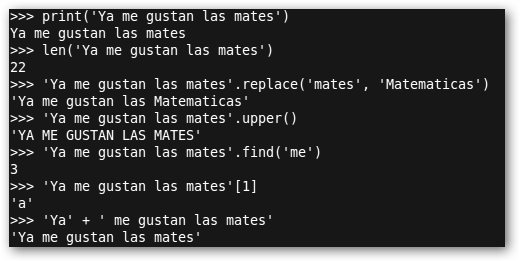
Si quieres saber los principios de diseño de Python, su Zen, escribe en la consola import this. Observa en la figura inferior el tratamiento de las cadenas en Python. Hemos imprimido la cadena (print), calculado su longitud (len), reemplazado una palabra por otra (replace), convertido a mayúsculas (upper) y encontrado una subcadena (find). Considera que el primer carácter de la cadena está en la posición 0, el segundo en la 1 (‘cadena’[1]), etc. Finalmente, hemos concatenado dos cadenas (‘+’). |
|
|
|
||
|
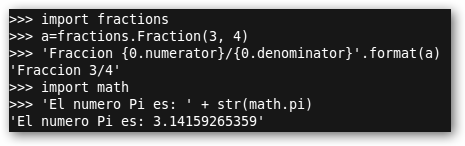
Mostramos dos ejemplos más sobre cadenas: formatear fracciones a la forma en la que estamos habituados (format) y la conversión de Π (math.pi) a cadena (str). |
||
|
|
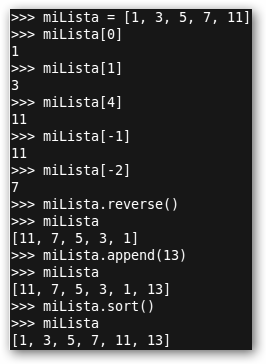
El manejo de las listas en Python es como se muestra en la ilustración: 1. miLista = [1, 3, 5, 7, 11] crea una lista. 2. Los elementos de la lista se enumeran empezando en 0: 1 es miLista[0], 3 es miLista[1], etc. 3. El último elemento está en la posición -1 (miLista[-1] es 11), el penúltimo en -2, etc. 4. miLista.reverse() invierte la lista. 5. miLista.append(13) añade 13 al final de la lista. 6. miLista.sort() la ordena. |
|
11.3. Estructuras de control y funciones.
|
Empecemos definiendo una función esPar con argumento n. Una función es un trozo de código que se define una única vez y puede ser llamado (utilizado) tantas veces como queramos. En Python, el ámbito de una función y de los bloques de código lo determina el identado. Dentro de esta función hay una estructura de control if if n % 2 == 0: |
|
se lee como: “si el resto de n con 2 es cero” (es decir, si n es par), entonces ejecuta el print(n,“Es par”) o instrucción inmediatamente a continuación (muestra el numero y el mensaje Es par). No ejecutaría nada más porque el identado del else: está al mismo nivel que el if.
Si no se cumple la condición: n %2==0, se ejecuta la instrucción siguiente al else: (en otro caso) print(n, “Es impar”).
esPar(3), esPar(8) son llamadas o invocaciones a nuestra función esPar.
Veamos otro ejemplo, la función “recursiva” máximo común divisor:
def mcd (a, b):
if a % b == 0:
return b
else:
return mcd(b, a % b)
Los bucles o ciclos están también presentes en Python:
|
while cond: bloque |
Ejecuta Bloque mientras se cumple la condición. |
Hablamos de Bloque porque no tiene porqué ser una única instrucción puede haber varias. El ámbito de este conjunto de instrucciones no lo designa ningún signo de puntuación (“;”, “{“, “}”, etc.) sino el identado.
Otro ejemplo de estructura de control es:
if condición1:
Bloque1
elif condición2:
Bloque2
else:
Bloque3
Si se cumple condición1 se ejecuta Bloque1 y acaba. Si no es así, se evalúa condición2. Si es verdadera condición2, se ejecutaría Bloque2. Si ambas condiciones son falsas sería la oportunidad de Bloque 3.
A continuación, se enseña cómo iterar sobre los elementos de una lista.
|
for e in lista: Bloque Así… for e in (2,4,6,8): print (e) … mostraría 2, 4, 6 y 8. |
Bloque se ejecuta tantas veces como elementos tiene la lista. En cada iteración “e” va avanzando en la lista y el ciclo se repite desde el primer elemento de la lista hasta el último. |
Considera una función un poco más interesante, el cálculo de la media aritmética de una lista:
def mediaAritmetica(lista):
suma = 0
for e in lista:
suma += e
print suma/float(len(lista))
# Observa que len(lista) devuelve la longitud de la lista y con float lo pasamos a flotante para que la división no sea entera. 7/2 es 3, porque “/” es la división entre dos enteros: 7 y 2. 7/float(2) es 3.5, porque “/” tiene dos operandos: un entero (7) y un flotante (float(2)).
11.4. Manejando ficheros y modos de trabajo con Python.
|
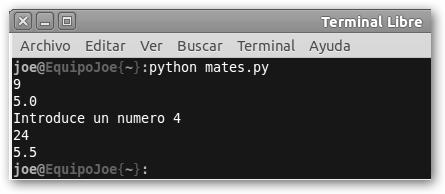
Conviene ahora destacar que Python puede ser utilizado de dos formas: 1.En modo interactivo: como hemos visto hasta ahora. 2. Mediante ficheros con extensión py, luego se ejecutan escribiendo en la consola: python nombreFuente.py en Linux o simplemente el nombre del fichero nombreFuente.py en Windows. |
|
||
|
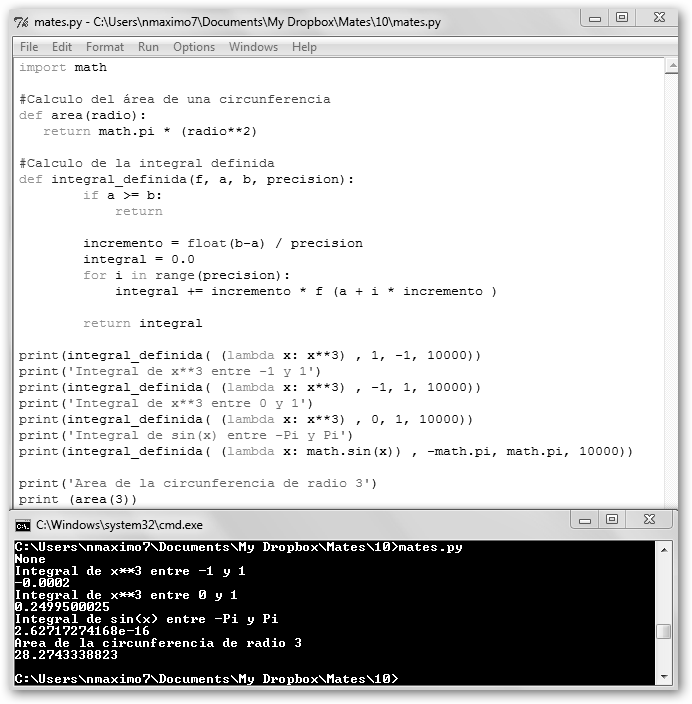
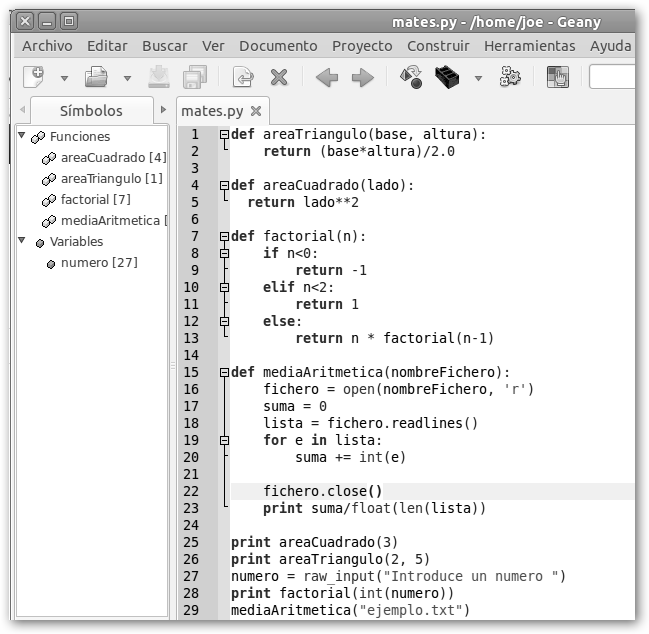
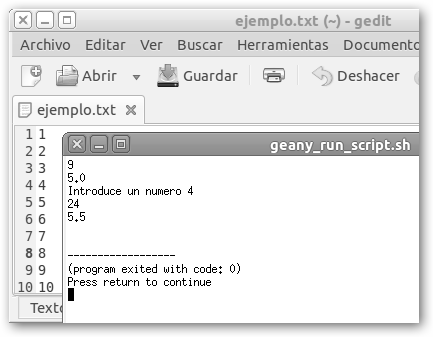
Se ha definido una función que calcula el área de la circunferencia (recuerda Pi*radio2) y otra, la integral definida de la función “f” desde “a” hasta “b”. Ésta se obtiene sumando las áreas de los rectángulos con base “incremento” y altura “f(a + i*incremento)” donde i varía entre 0 y precisión-1. Observa que con lambda definimos funciones anónimas (sin nombre), por ejemplo, x2 +1 sería lambda x: x**2 +1. A continuación, mostramos otro ejemplo realizado en Ubuntu. Definimos dos funciones bastante básicas: areaTriangulo y areaCuadrado que calculan las áreas de triángulos y cuadrados con las fórmulas clásicas: (base*altura)/2 y lado2. La función factorial se muestra como el ejemplo clásico del uso de la recursión en Python. Más interesante es mediaAritmetica, principalmente porque muestra cómo podemos trabajar con ficheros en Python. Esta función calcula la media aritmética de los números que están almacenados en el archivo que se le pasa como parámetro. Primero, abrimos el fichero en modo lectura: fichero = open(nombreFichero, 'r'). Luego, leemos “del tirón” todo su contenido en una única instrucción: lista = fichero.readlines(). Finalmente, liberamos los recursos que fichero está usando y reteniendo con fichero.close(). Si el archivo es muy voluminoso tendríamos que plantearnos leerlo línea a línea, por ejemplo: for linea in fichero: print linea También, se ilustra como leer datos desde consola (numero = raw_input("Introduce un numero ")) y realizar la conversión de texto a entero (int(numero)).
|
|||
11.5. La tortuga más “compleja”.
Veamos ahora como ser capaces de visualizar las dos formas de escribir los complejos: cartesianas x + iy y polares (r, theta). Utilizamos Turtle que nos permite crear gráficos sencillos haciendo uso de nuestra amiga la tortuga.
|
1 import turtle 2 import cmath 3 def muestrameComplejo(x, y): 4 t=turtle.Pen() 5 t.showturtle() 6 t.shape("turtle") 7 t.color("red") 8 t.pensize(10) 9 t.goto(x, y) 10 s= turtle.Screen() 11 s.delay(100) 12 t.home() 13 t.penup(); 14 t.forward(200) 15 t.pendown(); 16 t.color("blue") |
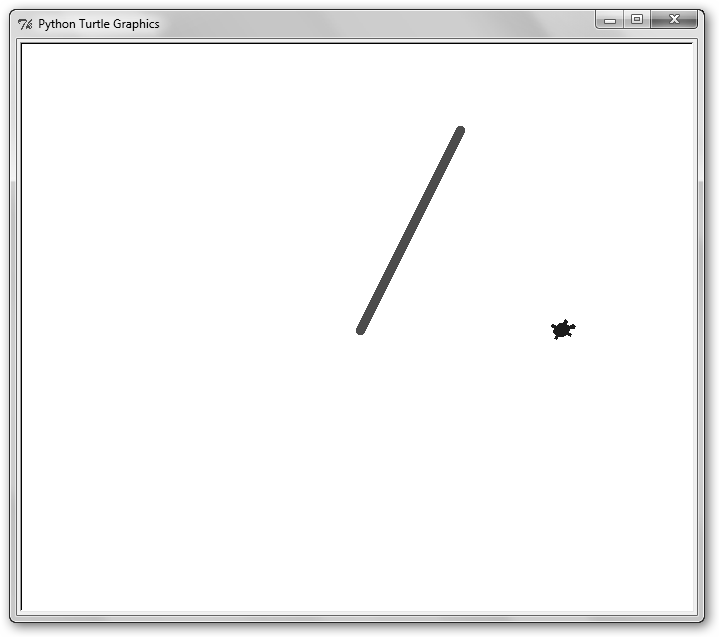
Importamos las librerías turtle y cmath (líneas 1 y 2). Creamos la función muestrameComplejo con dos argumentos: la parte real y la imaginaria del complejo. Creamos un lápiz (4) e indicamos que cuando pinte muestre la tortuga (5, 6) de color rojo (7) y que su trayectoria sea de un grosor 10 (8). Luego, le decimos que se desplace a (x, y) en la línea 9 y con estas instrucciones hemos dibujado nuestro complejo en coordenadas cartesianas. Para que se vean claramente los dos vectores, creamos un objeto Screen “s” (10) e invocamos a su método delay para que se demore un poco en realizar la siguiente instrucción (11). A continuación, lo posicionamos en la casilla inicial de partida (12) y lo movemos 200 a la derecha (14) pero sin pintar su trazo (13) para que se puedan ver los dos vectores. En la línea 15 volvemos a indicar que se pinte la trayectoria de la tortuga y en la 16 cambiamos su color a azul. |
|
17 t.radians() 18 t.left(cmath.phase(complex(x, y))) 19 print("Dibujando el complejo:", x, "+", y, "i") 20 t.forward(abs(complex(x,y))) 21 s.delay(300) 22 turtle.bye() |
En la línea 17 indicamos que indicaremos al galápago la dirección a donde se debe mover en radianes. Más concretamente, se va a mover en la dirección del argumento de nuestro complejo (cmath.phase(complex(x,y)), línea 18) el módulo del complejo (abs(complex(x,y), 20) con lo que creamos el vector en coordenadas polares. A continuación, hacemos una paradita en la ejecución del programa (21) y cerramos la ventana gráfica (22). |
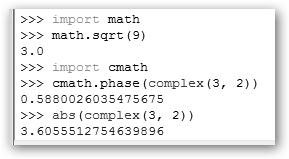
A partir de ahora, podremos invocar la función tantas veces como deseemos, por ejemplo, muestrameComplejo(100, 200) devuelve el resultado que ilustra en la figura.

11.6. Cálculo simbólico con SymPy
SymPy es una librería que aporta a Python la capacidad de cálculo simbólico. Instala el paquete en Windows desde su portal web http://docs.sympy.org/. Para trabajar en Ubuntu vamos a instalar el entorno IPython, la librería SymPy y otras más que luego necesitaremos. Escribe en la consola sudo apt-get install python-sympy ipython python-matplotlib python-numpy python-scipy.
|
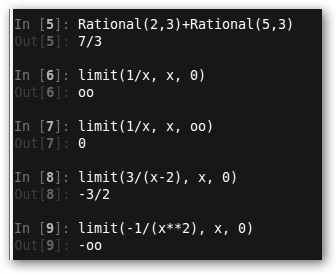
Lanzamos IPython (un entorno de Python) en Ubuntu desde el terminal, escribiendo ipython –pylab. Veamos lo que podemos realizar con esta librería: * Para trabajar con ella debemos primero importarla (In[1]) * In[2]: Definimos x como una de nuestras variables. * In[3]: Desarrollo en serie de Taylor de la exponencial (exp(x)), en el punto 0. * In[5]: Suma de fracciones. * In[6]-In[9]: Solicitamos la realización de distintos límites. |
En IPython las líneas de entrada están enumeradas (In[1], In[2], etc.), así como, las salidas (Out[1], Out[2], etc.).
Observa que el infinito se escribe así “oo”, es decir, dos “o” minúsculas. Podemos también solicitar la derivada n-ésima: diff(x**2+8*x-4+sin(2*x), x, 2) devuelve 2 - 4*sin(2*x). |
|
|
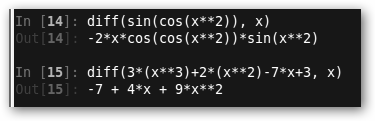
* In[14] , In[15] e In[17]: Derivamos varias funciones. ¡Fíjate!, siempre tienes que indicar sobre que variable. |
|
|
|
* In[18]: Realizamos la integral indefinida de la salida Out[17], es decir, de -7+4x+9x2. * In[19]: Solicitamos una integral definida de la función 2cos(x)+sin(x) en el intervalo [0, Pi]. |
|
|
|
* In[22]: Agregamos “y” como otra variable lista para usar. * In[23] e In[24]: Expandimos varias expresiones. Sería el concepto contrario a la simplificación. |
|
|
|
* In[33] e In[37]: Resolvemos sistemas de dos y tres ecuaciones con dos y tres incógnitas respectivamente. * In[35]: Resolvemos la ecuación Out[34] y obtenemos que sus dos raíces son 7 y -5. Ya lo sabíamos pues en In[34] habíamos solicitado expandir la expresión (x-7)2(x+5)2. |
Observa que si queremos resolver el sistema x+y=2, 2x+y=5, se pasan como: x+y-2 y 2x+y-5. Además, la sintaxis completa sería: solve([ec1, ec2, ec3], [x, y, z]). |
|
|
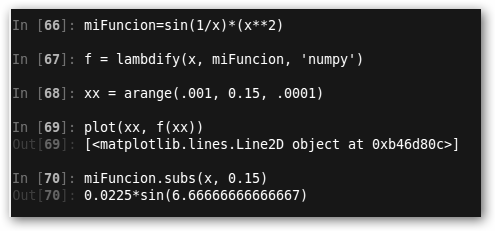
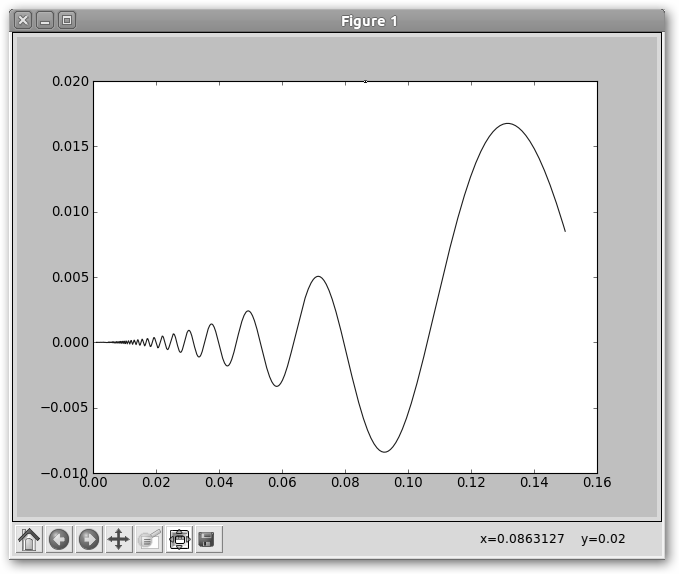
* In[66]: Definimos una función. * In[67]: Transformamos nuestra función en una función lambda conveniente para cálculos numéricos posteriores. Indicamos que las funciones definidas en ella las tome de numpy (el seno). * In[68]: Vamos a graficar nuestra función. Definimos el rango en el vector x. Queremos como punto inicial .001, como punto final 0.15 e incremento .0001 * In[69]: Graficamos nuestra función con plot y como argumentos: la función y el rango de valores. * In[70]: Evaluamos nuestra función en 0.15. |
Con miFuncion.subs(x, 0.15).evalf() indicaríamos que nos muestre un valor numérico. |
|
|
|
||
|
* In[74]-In[76]:
Con Sympy podemos trabajar con expresiones lógicas y
comprobamos si varias expresiones pueden satisfacerse. Desde
luego x & ~x (“x” y “no x”) va a ser
que no, |
Observa que &, |, ~ son nuestro “y” (˄), “o” (˅)y la negación. Probemos otras cosas: integrate(x+sinh(x), x), integrate((x+y)**2, x), cos(x).series(x, 0, 10), (pi+exp(1)).evalf() (evalúa Pi+e), etc. |
|
|
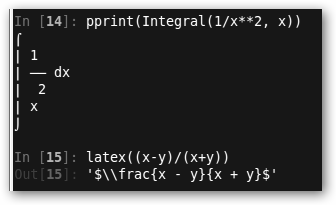
* In[14]: También podemos escribir con SymPy nuestras expresiones de la forma “natural” en la que estamos acostumbrados. * In[15]: Muestra el código LaTex de una expresión. |
|
|
|
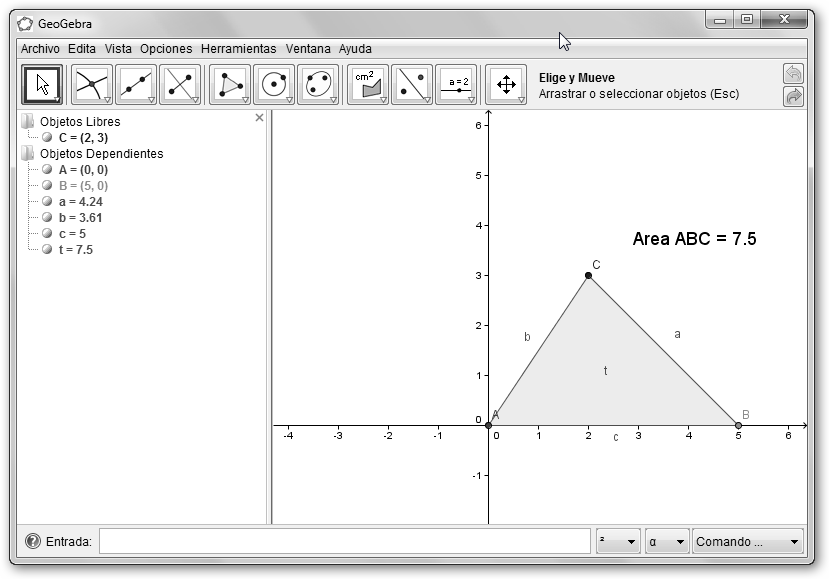
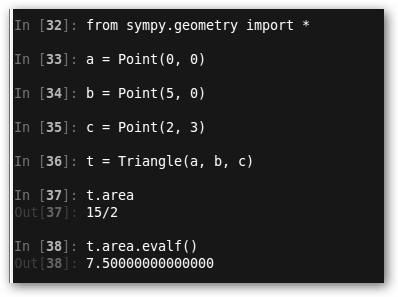
También podemos hacer Geometría con SymPy. Hemos creado un triángulo y calculado su área. Prueba: c = Circle(a, 5); c.area (25Π), intersection(c,t) (5, 0), etc. |
c.is_tangent(Line(Point(5,0), Point(5, 5))), ¿es tangente la línea que pasa por (5,0) y (5, 5) a la circunferencia de centro (0, 0) y radio 5. La respuesta es True, verdadero. Sin embargo, c.is_tangent(Line(Point(5,0), Point(3, 5))) devuelve falso. |
|
11.7. NumPy, SciPy y matplotlib: todos para uno, uno para todos.
Navega a su portal web http://www.scipy.org/SciPy y descarga NumPy y SciPy para tu plataforma, haz lo propio con matplotlib.sourceforge.net. ¡Mucho cuidado con las versiones tanto de Python como de las librerías, pueden ser incompatibles! Matplotlib está orientado a la representación gráfica, mientras que las otras dos nos permiten trabajar con arrays numéricos, matrices, realizar programación matemática avanzada, procesamiento de señal y estadística. ¡Tengo que advertirte que estas librerías ofrecen poco soporte a la familia de sistemas operativos Windows en general y a Windows 7 en su versión de 64 bits! En particular, para esta demostración se utilizó la versión Python 2.6: Windows x86 MSI Installer(2.6.6).
|
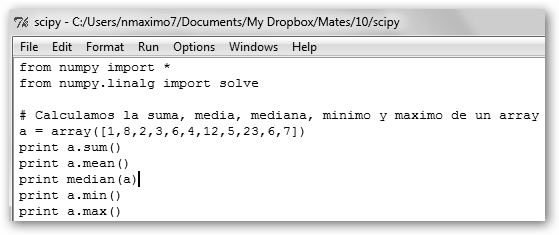
Nada más abrir Python, selecciona File, New Window. Esto nos permitirá guardar nuestro trabajo en un fichero y si nos equivocamos, no precisaremos teclear de nuevo todas las órdenes. Las primeras dos líneas importan las funciones de las librerías que necesitamos. |
|
|
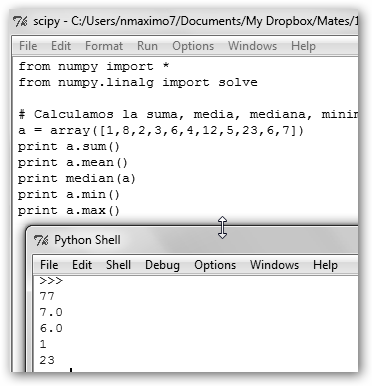
A partir de ahí definimos un array a = array([1,8,…,7]) y calculamos la suma, la media, la mediana, su mínimo y su máximo. En Python 3, la llamada print a.sum() no funciona, deberás escribir print(a.sum()). |
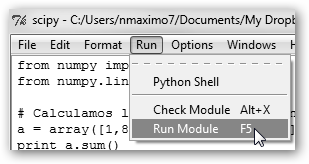
Navega por el menú Run, la opción Run Module o la tecla rápida F5 para ejecutar el módulo que acabamos de escribir. |
|
|
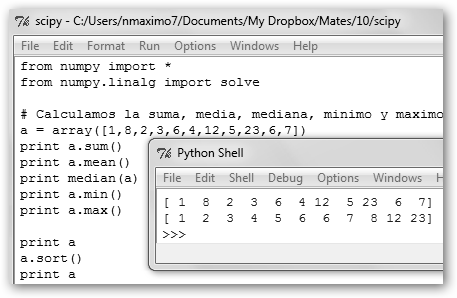
A continuación, vamos a ordenar el array. Incluso podríamos indicar el método de ordenación con a.sort(kind='mergesort'). Otras opciones son quicksort y heapsort. |
|
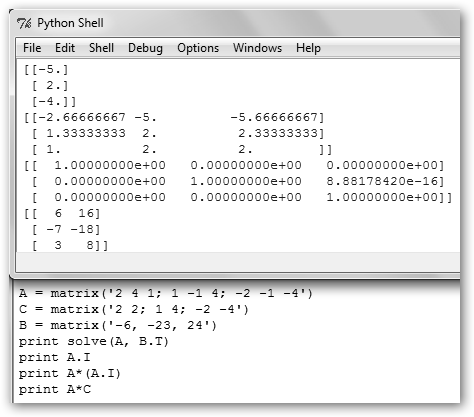
Tratemos ahora de resolver el siguiente sistema de ecuaciones:
Lo
podemos expresar como la matriz de coeficientes A y la de términos
independientes B; para solucionar el sistema se llama a la función
solve(A, B.T). Observa que B.T es la matriz transpuesta de B. La
solución se puede observar en la Shell de Python: -5, 2 y -4. A
continuación, calculamos la matriz inversa de A, la multiplicamos por si
misma (no nos fiamos |
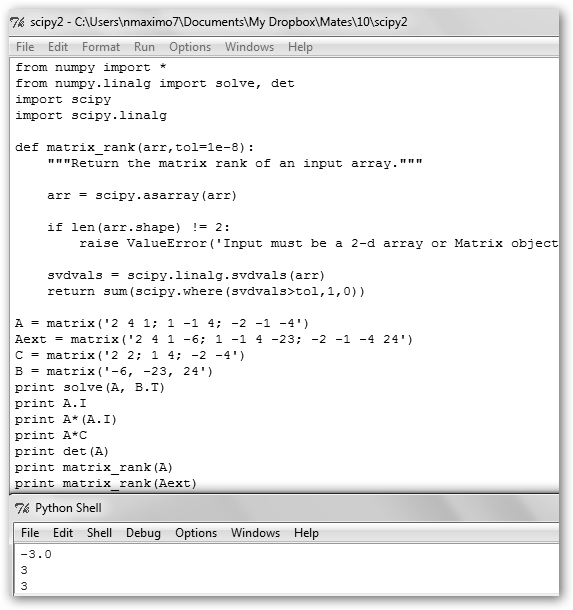
Comprobemos a continuación que el sistema de ecuaciones debía tener una única solución. |
|
Observa la segunda línea: from numpy.linalg import solve, det, hemos importado una nueva función det, para calcular el determinante de A con det(A), es igual a -3. Luego, comprobamos que el rango de la matriz de coeficientes (matrix_rank(A)) y la extendida (matrix_rank(Aext)) son iguales a 3 y como el número de ecuaciones 3 es igual al número de incógnitas, volvemos a tener un sistema de ecuaciones compatible y con una única solución. Sin embargo, no encontramos soporte nativo para la función rango, hemos tenido que utilizar una propuesta (pero todavía no oficial) en http://osdir.com/ml/python.numeric.general/ 2006-02/msg00154.html. |
|
|
|
¡Cambiemos de sistema operativo! ¿No era Python multiplataforma? Recuerda que ya instalamos en el apartado anterior las librerías necesarias. Desde un terminal escribe ipython –pylab para iniciar la sesión, con el argumento pylab podemos trabajar interactivamente con mathplotlib. |
|
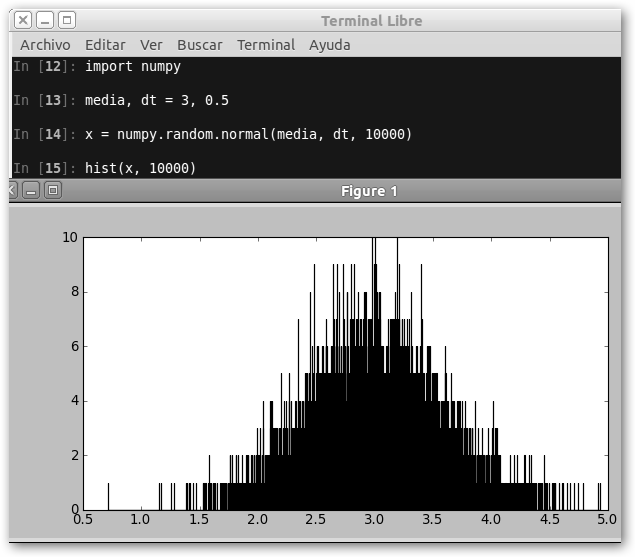
|
Observa que hemos importado la librería numpy, definido dos variables que serán la media y la desviación típica: media, dt. Con x generamos una colección de números aleatorios que siguen una distribución normal de media 3 y desviación típica 0.5. El tercer argumento de normal es el número de elementos que se desea que se generen. Este último dato también es necesario para que hist nos muestre el histograma. |
También puedes observar otras distribuciones, por ejemplo, chi-cuadrado χ2 o la T de Student con 2 grados de libertad: z = numpy.random.chisquare(2, 10000) o z = numpy.random.standard_t(2, 10000); hist(z, 10000).
Vamos a utilizar un fichero de alturas y pesos de hombres y mujeres (alturaPeso) con el siguiente formato:
|
AlturaH AlturaM PesoH PesoM 1,61 1,53 72,21 50,07 1,61 1,60 65,71 59,78 1,70 1,54 75,08 50,66 1,65 1,58 68,55 56,96 1,72 1,61 70,77 51,03 1,63 1,57 77,18 64,27 1,76 1,61 81,21 68,62 1,67 1,52 75,71 54,53 1,67 1,62 76,57 66,96 1,65 1,63 68,78 66,94 1,63 1,55 65,13 59,84 1,70 1,60 77,53 55,46 […] |
|
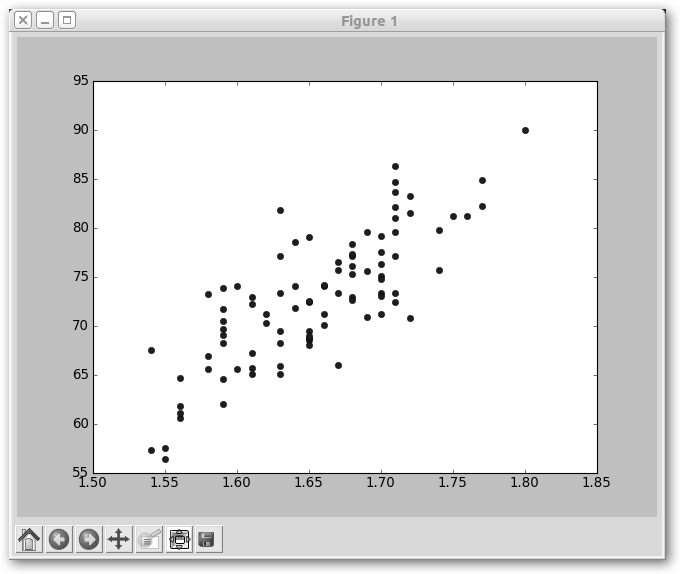
Observa las dos líneas de código: 1. alturah, alturam, pesoh, pesom = numpy.loadtxt('alturaPeso', unpack=True, skiprows=1). En la primera línea leemos el archivo alturaPeso. Con el segundo argumento unpack=True indicamos que las distintas columnas las vamos a leer en las variables alturah, alturam, pesoh y pesom. |
2. Con plot(alturah, pesoh, ‘o’) dibujamos la relación existente entre la altura y el peso de los hombres. Observa la figura inferior. |
|
|
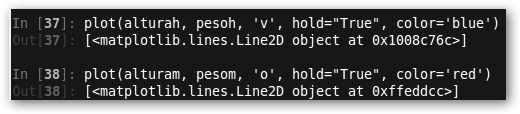
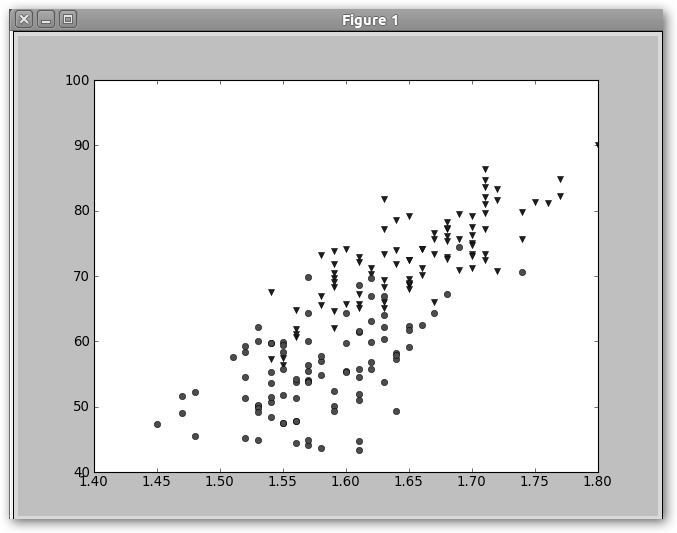
3. Comparemos los dos géneros: los varones los pintaremos como triangulitos azules (‘v’) y las mujeres como círculos rojos (‘o’). Observa el argumento hold=”True” para poder superponer los dos gráficos.
En ambos casos se observa una clara relación entre altura y peso. |
|
|
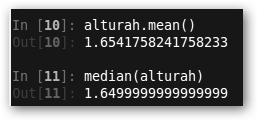
4. Fíjate como puedes calcular la media y la mediana de la altura de los hombres:
|
|
|
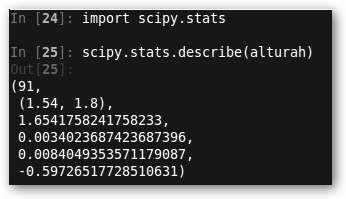
5. En la librería scipy.stats tenemos un buen número de funciones de utilidad (scipy es tan grande que tenemos que importar sus partes por separado), por ejemplo describe. Ésta devuelve el tamaño de la muestra, el mínimo y el máximo, la media aritmética, la varianza, los coeficientes de asimetría y curtosis. |
|
|
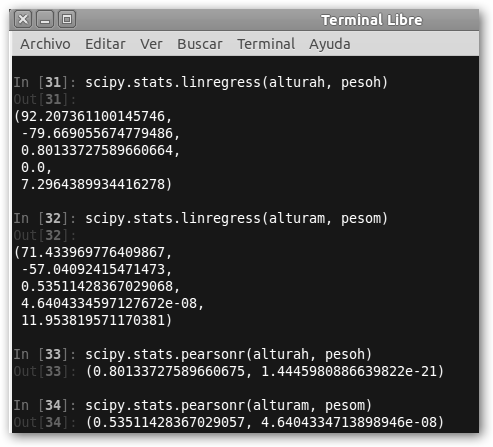
6. La función pearsonr calcula la relación entre dos conjuntos. El primer valor que devuelve es el coeficiente de correlación de Pearson y el segundo la probabilidad asociada. Independiente del género, la altura y el peso están relacionados pues las probabilidades están muy próximas a cero y nos permite rechazar la hipótesis de independencia. 7. linregress devuelve la recta de regresión. Más concretamente, la pendiente, el término independiente, el coeficiente de Pearson, su probabilidad asociada (nivel de significación) y la desviación típica del error estimado. |
|
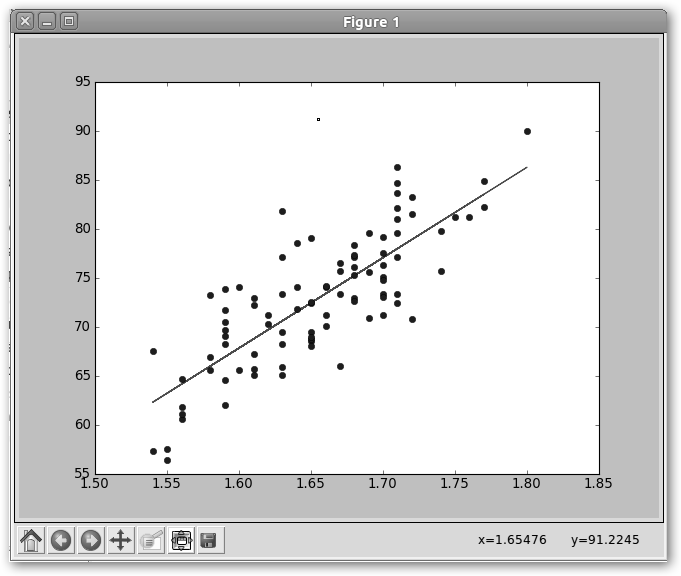
Comprobamos gráficamente que la recta de regresión que nos propone linregress se ajusta a los puntos. Observa que con pylab.plot dibujamos tanto la recta de regresión como la nube de puntos de las alturas y los pesos. Para la recta de regresión tomamos como “X” la altura de los varones (alturah) y como “Y” independiente + pendiente*alturah. |
Para realizar este test es necesario que ambas muestran tengan distribuciones normales y la misma varianza. |
|
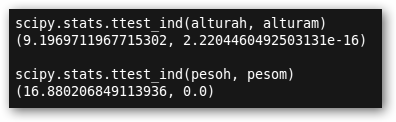
8. La función ttest_ind realiza un T-test, un contraste sobre las medias de dos muestras independientes y devuelve el estadístico t y la significación. Como en ambos casos las probabilidades están muy próximas a cero (p.05) se rechaza la hipótesis nula de igualdad de medias, es decir, la media de los pesos y las alturas son distintas por géneros. |
|
|
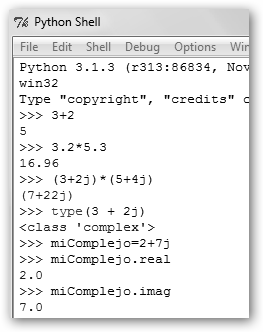
9. La función levene realiza el test de Levene que comprueba la hipótesis nula de que las muestras pasadas como argumento tienen la misma varianza. Devuelve el estadístico y el nivel de significación, en ambos casos mayor a .05. No rechazamos la hipótesis nula, aceptamos que las varianzas son homogéneas y podemos aplicar “sin problemas” el contraste de hipótesis anterior. |
Prueba: x = numpy.random.normal(0, 1, 10000); y= numpy.random.normal(0, 1, 10000); scipy.stats.ttest_ind(x, y) y scipy.stats.levene(x, y) indican que “x” e “y” pertenecen a poblaciones con la misma media y varianza. |
Ahora teclea z = numpy.random.normal(2, 5, 10000), realiza los test: scipy.stats.ttest_ind(x,z) y scipy.stats.levene(x,z) ¿Qué ha sucedido? Pues que el resultado es justamente el contrario, las poblaciones de dónde se han extraído estas muestras deben diferir en media y varianza.





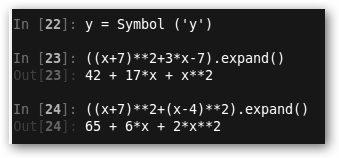

 se ponga nuestro amigo como se ponga.
se ponga nuestro amigo como se ponga.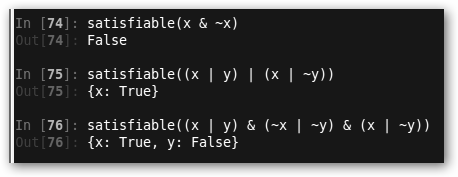
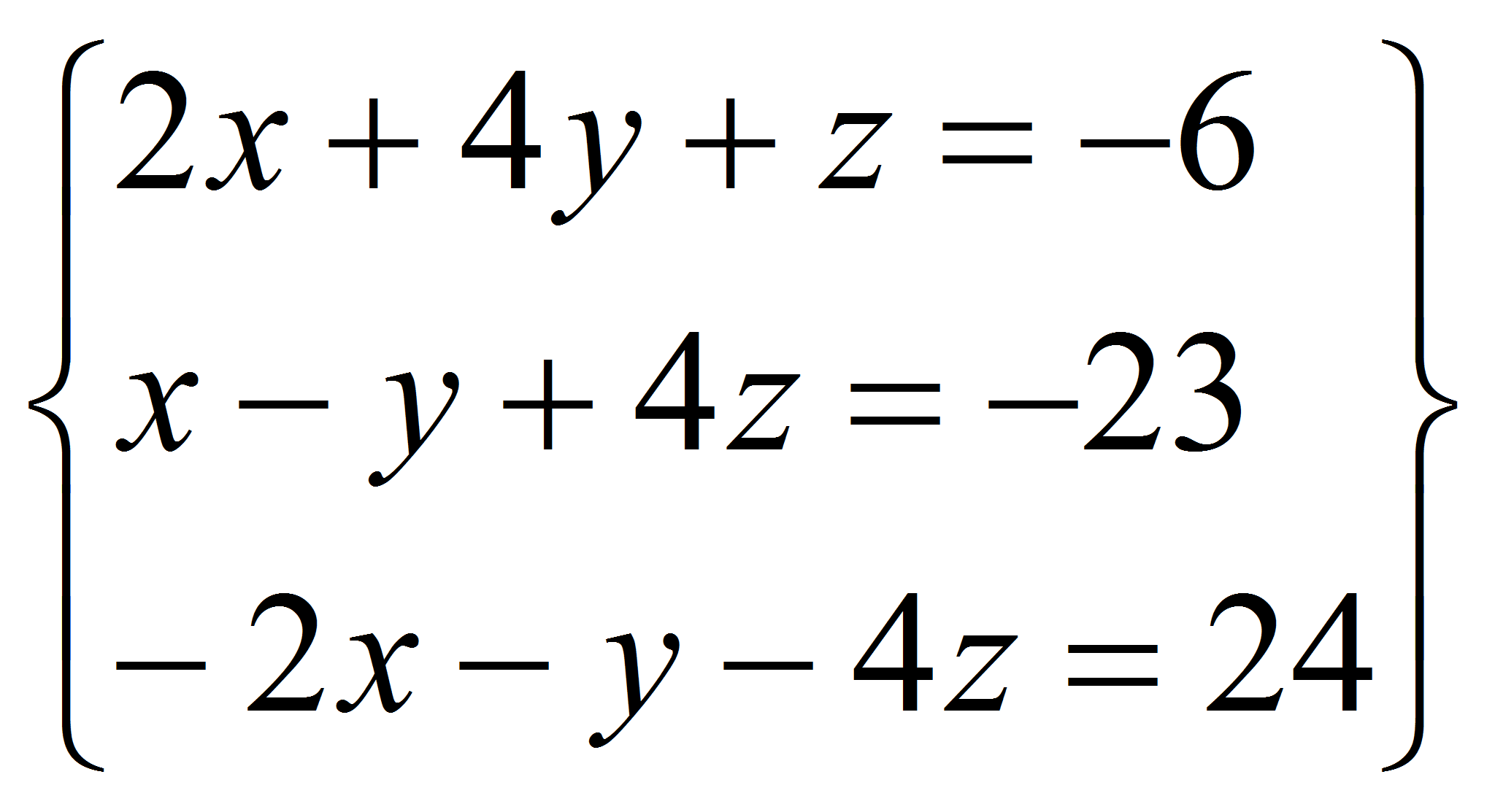
 )
y por otra matriz C (A*C).
)
y por otra matriz C (A*C).