10. Matemáticas avanzadas II: ¡Si al final me gustan!
10.1.2. ¿Cómo obtenerlo y utilizarlo?
10.1.3. ¡Tú lo has querido forastero!
10.2. Teoría de grafos con GraphThing
10.3. Planificación de proyectos
10.4. Programación lineal con GLPK
10.5. GSL shell: Gráficos 3D, Ajuste no lineal, EDO, etc.
10.6. EDO’s y “otras hierbas” con Axiom
10.1. Sage.
10.1.1. ¿Qué es?
Sage son las siglas de Software for Algebra and Geometry Experimentation, es decir, software para la experimentación en álgebra y geometría. Se trata de un software matemático de código libre (liberado bajo una licencia GPL). No trata de reinventar la rueda sino que utiliza el mayor número de programas y paquetes libres disponibles bajo una única interfaz. Bajo este mantra consigue dos objetivos: flexibilidad (capacidad de resolver problemas muy diversos) y potencia.
Es una alternativa “real” a los programas comerciales: Magma, Maple, Mathematica y Matlab y si programas en Python puedes extraer su máxima potencia.
10.1.2. ¿Cómo obtenerlo y utilizarlo?
Hay dos modos de conseguirlo:
1. Utilizando Sage OnLine: más sencillo imposible, no requiere instalación pero si una buena conexión de Internet, a veces va lento y otras simplemente no va.
2. Descargando en el botón Download 4.6 una máquina virtual. El principal inconveniente es la dificultad de la instalación. Como ventaja está que tendrás a tu disposición una potente herramienta libre, no precisarás acceso a Internet y el sistema funcionará “como las balas”.
|
¡No más esperas! Empecemos por la opción 1. Navega a http://www.sagemath.org/. Haz clic en Try Sage Online y tendrás que crearte una cuenta dando tu nombre, contraseña y e-mail, así como, confirmar el correo que recibirás. |
|
|
Si es la primera vez que accedes tendrás que hacer clic en Sign up for a new Sage Notebook account, registrarse para una cuenta en el cuaderno de trabajo de Sage. |
Sage trabaja con hojas de trabajo como por ejemplo Calc o Excel. Haz clic en New Worksheet, nueva hoja de trabajo para crearte una. |
|
Si tienes dudas sobre alguna orden escribe orden?, por ejemplo, divisors?. |
Esas hojas de trabajo puedes editarlas (Edit), compartirlas (Share), publicarlas (Publish), imprimirlas (Print), etc. Observa un cuadrito, escribe 7+5 y haz clic en evaluate. En el ejemplo de la izquierda hemos realizado varios cálculos aritméticos, el límite de sin(x)/x cuando x tiende a cero, derivado x2+4x-6, integrado 2x+4 y solicitado los divisores de 30 |
|
|
En la siguiente figura se ha realizado lo siguiente: *
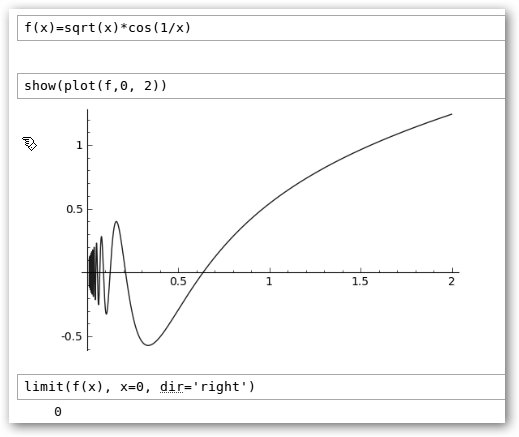
Definido una función: f(x)= * Graficado dicha función en el intervalo [0, 2]: show(plot(f, 0, 2)). * Calculado el límite de la función en cero por la derecha: limit(f(x), x=0, dir=’right’). Si hubiéramos escrito limit(f(x), x=0) sería el límite en 0 y si sustituimos ‘right’ por ‘left’ sería el límite a la izquierda. |
|
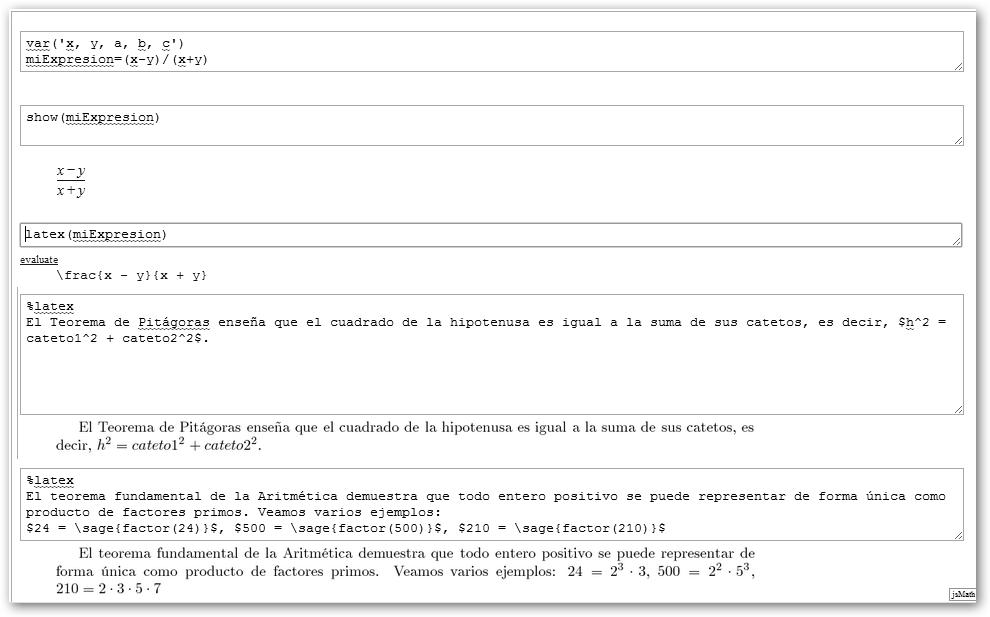
Observa en la ilustración que hemos definido una expresión o fórmula matemática: miExpresion=(x-y)/(x+y). La orden previa var(‘x, y’) es necesaria para indicar a Sage que “x” e “y” son dos variables con las que vamos a trabajar. Con show(miExpresion) mostramos nuestra fórmula tal como estamos acostumbrados a verla en nuestro día a día y en centros de estudio y tiene como objetivo enseñar nuestros resultados de una forma conveniente cuando publiquemos o imprimamos nuestra hoja de trabajo. Más interesante aún, con latex(miExpresion) tienes el código LaTeX que puedes insertar en cualquier editor de LaTeX para disponer de la expresión. Recuerda que debes encerrar el código con el signo dólar “$” para indicar que es una expresión matemática. Además, con latex expresión, podemos trabajar con LaTeX en Sage ¡con la ventaja adicional que podemos llamar a funciones de Sage!: \sage{factor(210)}. |
|
|
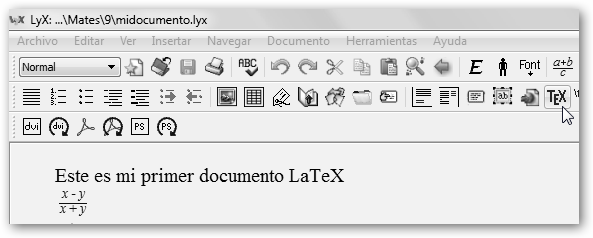
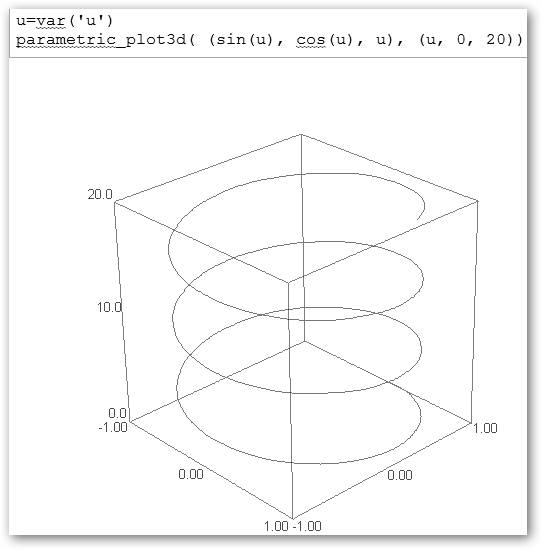
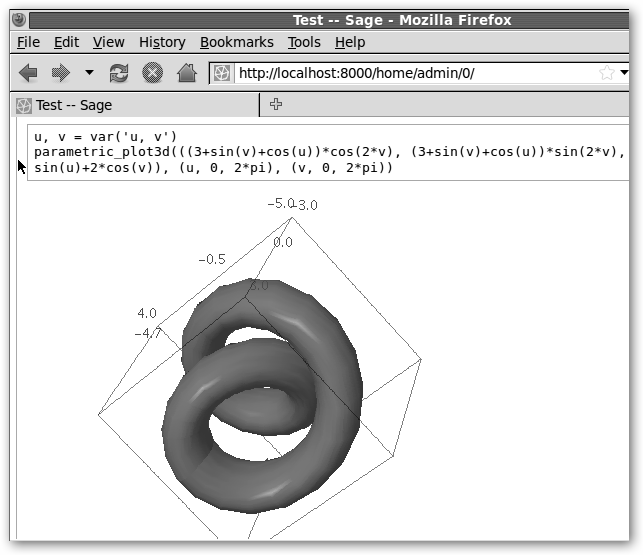
Observa como en LyX hay un botón para incrustar directamente código LaTeX en tus documentos. Finalizamos mostrándote la potencia con un grafo 3d en ecuaciones paramétricas. Prueba ahora: sumar fracciones con 3/2+7/4 (13/4); 7.is_prime() (¿es primo 7?); integrate?? mostrará información y ejemplos sobre la función integrate; integrate(x^3+cos(x), x) integramos x3+cos(x); derivative(sin(cos(x)), x, 3), solicitamos la derivada tercera; dibujar cuerpos geométricos: cube(), sphere(), octahedron(),icosahedron(), dodecahedron(), tetrahedron(), … Trabajemos con matrices: 1. Definición: miMatriz = random_matrix(ZZ, 5, 5). 2. Determinante: miMatriz.det(). 3. Rango: miMatriz.rank(). 4. Matriz inversa: miMatriz.inverse(). 5. Polinomio característico: miMatriz.charpoly(). 6. Autovalores: miMatriz.eigenvalues(). |
Teclea lo siguiente: var('a, b, c') solve(a*x^2+b*x+c==0, x) Sage resolverá una ecuación de segundo grado genérica. ¿Y si no tiene raíces reales? solve(x^2+10, x) devolverá [x == -I*sqrt(10), x == I*sqrt(10)] donde I es el número imaginario. var(‘x,y,z’) solve([2*x-4*y+5*z==10, -2*x-2*y-5*z==-22, 2*x-y-3*z==0], x, y, z) resuelve el sistema de ecuaciones propuesto: (4, 2, 2). Otra forma de resolverlo sería: matrix(3, [2, -4, 5, -2, -2, -5, 2, -1, -3]).inverse()* vector([10, -22, 0]) o simplemente matrix(3, [2, -4, 5, -2, -2, -5, 2, -1, -3]) \ vector([10, -22, 0]) . |
10.1.3. ¡Tú lo has querido forastero!
|
Con la versión online has quedado frustrado por su lentitud. ¿Qué hacer? Navega a www.virtualbox.org y descarga VirtualBox. Con el podrás crear máquinas virtuales, es decir, tendrás otros sistemas operativos dentro de tu Windows pero de forma completamente segura, “encerradas” en discos virtuales. Descarga y descomprime también la máquina virtual de Sage (sage-vmware-4.6.zip) desde http://www.sagemath.org/ en la sección Download, Windows, RedIRIS. Arranca Virtual Box desde Inicio, Todos los programas, Oracle VM VirtualBox, VirtualBox. |
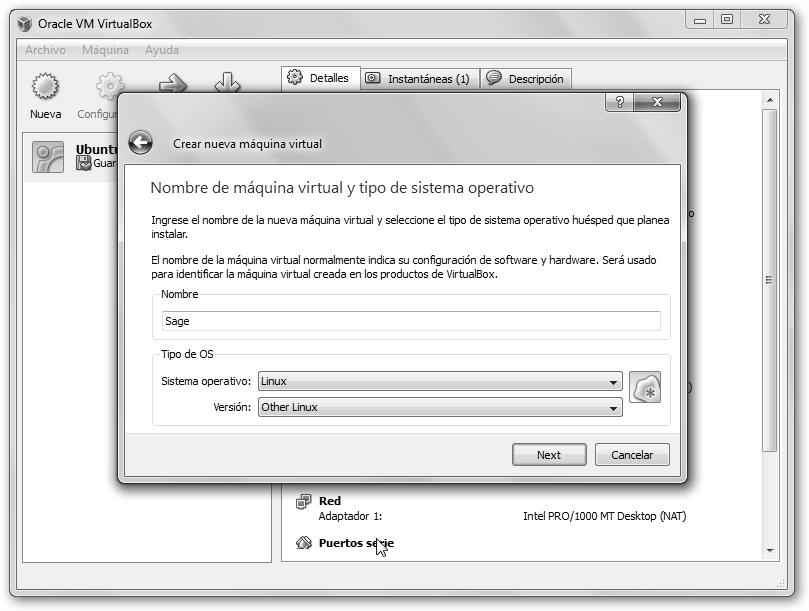
Crea una máquina virtual haciendo clic en el botón Nueva, en el menú Máquina, opción Nueva… o con las teclas rápidas Ctrl y N. |
|
Comenzará un asistente, dale un nombre a la máquina virtual (p.e. Sage), elige como sistema operativo Linux y en Versión Other Linux. |
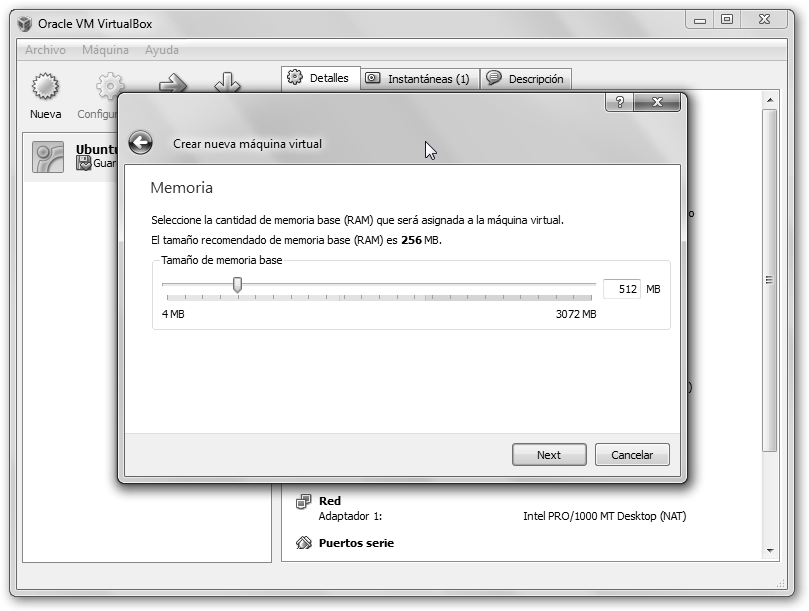
Asigna un tamaño de memoria base a la máquina virtual, 512 MB suele ser un valor aconsejable para la mayoría de las configuraciones. |
|
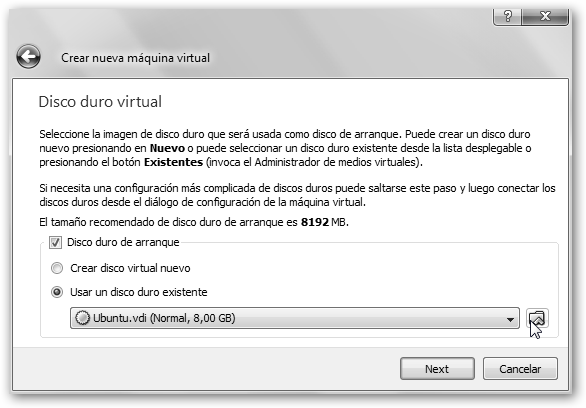
Ahora necesitamos un disco virtual. Haz clic en Usar un disco duro existente y navega a la carpeta donde hayas descomprimido la máquina virtual de sage. ¡No donde esté el archivo zip! Precisas previamente descomprimirlo.
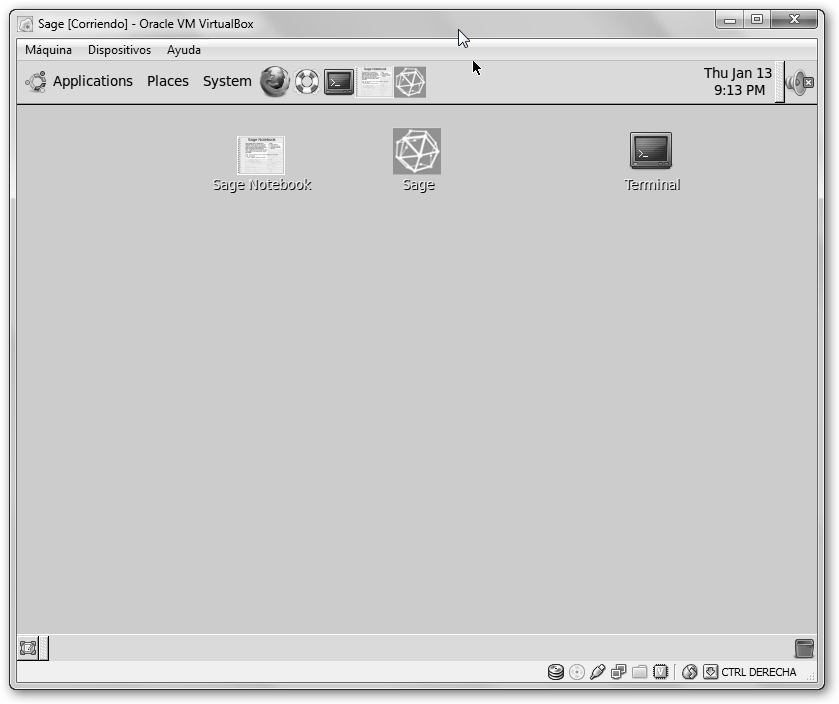
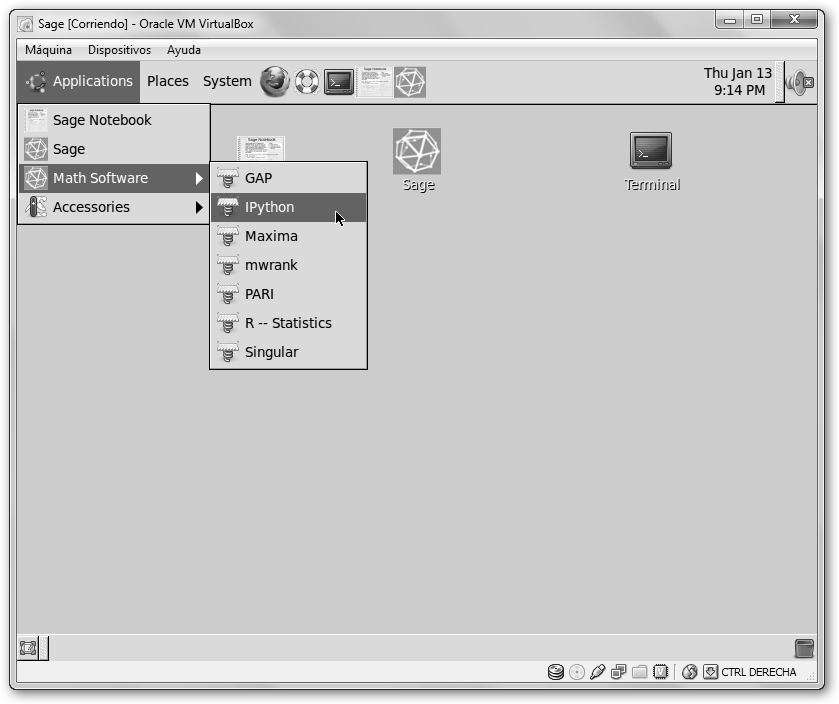
Observa tu máquina virtual sage. En Applications, Math Software tienes varios programas. El nombre de usuario y contraseña es sage. |
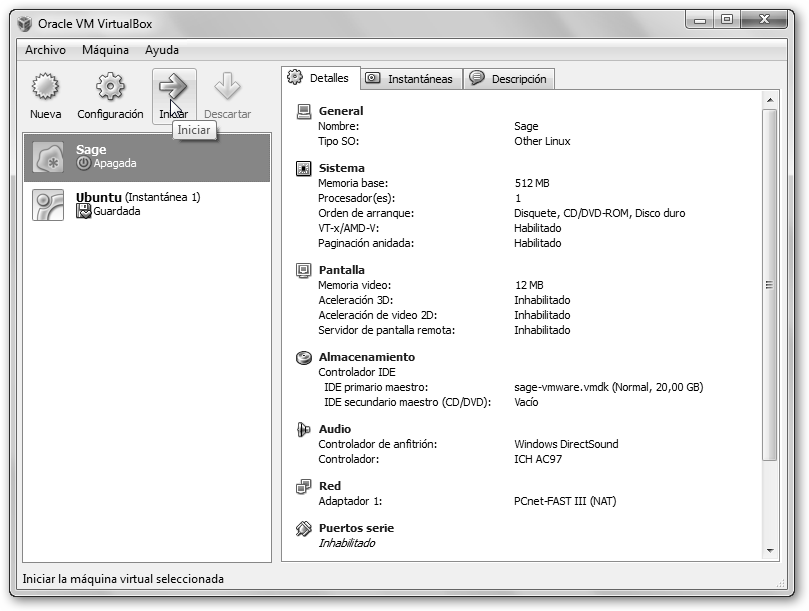
Una vez indicado el disco duro existente has creado tu máquina virtual Sage y ya estás preparado para empezar a trabajar con ella. Selecciónala (puedes tener varias máquinas virtuales, en la figura hay dos: Sage y Ubuntu) y haz clic en la flecha Iniciar. |
|
|
|
|
El elemento principal es el acceso directo o lanzador en el escritorio central Sage. Sin embargo, antes de hacer clic sobre él, precisaremos configurar el teclado.
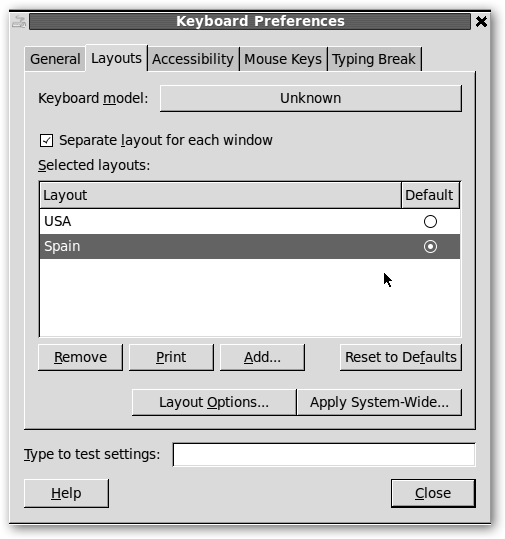
Navega por System, Preferences, Keyboard, es decir, Sistema, Preferencias, Teclado. |
|
|
|
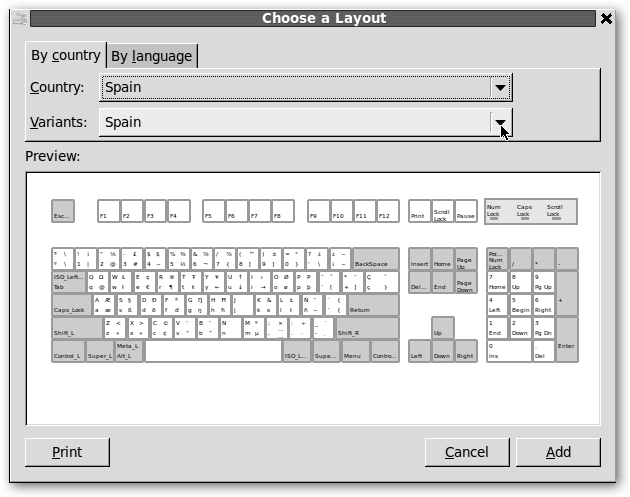
En la pestaña Layouts añade (Add…) el teclado español (Spain).
A continuación, haz clic en el acceso directo Sage y
escribe notebook(). Para estos …
|
|
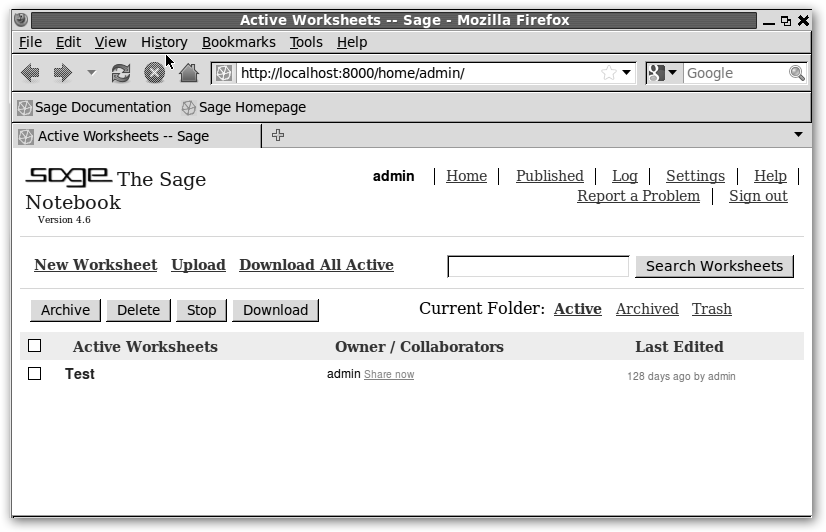
Observa la ventana principal, es bastante parecida a la versión online. Haz clic sobre la hoja de trabajo Test y comprueba distintas solicitudes a Sage. En particular, ¿a qué mola el icosaedro? Puedes moverlo a placer. |
|
|
|
A la izquierda se muestra una gráfica 3d con coordenadas paramétricas. ¡Los límites los pones tú con tu esfuerzo e imaginación! También, puedes graficar en 3D en la forma habitual: x, y = var(‘x, y’) plot3d(exp(-x*x)*exp(-y*y), (x, -2, 2), (y, -2, 2)). También, puedes acceder a otros programas desde Sage: maxima(‘solve ([2*x+2*y=6], [x, y]’), singular(‘4+7’), gap(‘1/3+2/5’), etc. |
10.1.4. Sage interactivo
|
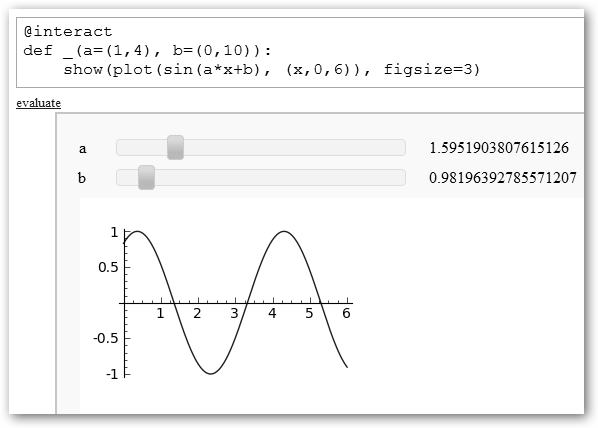
Si buscas ayuda sobre un comando en Sage, ya hemos comentado que sólo tienes que escribirlo seguido de dos símbolos de interrogación: interact??. Encontrarás no sólo abundante información sino código listo para “copiar y pegar”. En este caso nos enseña cómo tener en Sage una herramienta interactiva. |
|
|
|
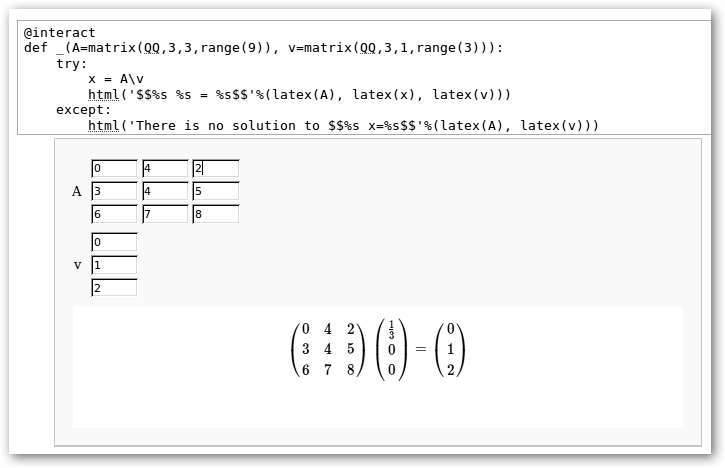
Estos ejemplos están incluidos en la ayuda de Sage. Estas ilustraciones nos permiten observar los cambios en gráficas 2D y 3D conforme cambiamos sus parámetros, así como, poder resolver cualquier sistema de ecuaciones cambiando dinámicamente la matriz de coeficientes (A) y el vector de términos independientes (v). |
|
|
|
10.2. Teoría de grafos con GraphThing.
|
|
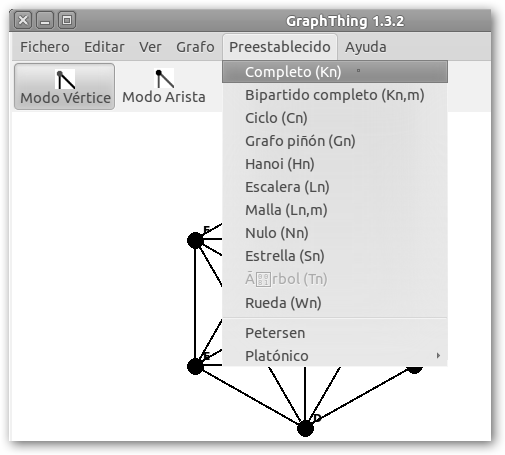
Si quieres estudiar o recordar un poco de Teoría de grafos utiliza GraphThing en graph.seul.org o instala el paquete graphthing en Ubuntu, Debian y derivados. Tiene muchos grafos preestablecidos en la entrada de menú Preestablecido: Completo, Rueda, Ciclo, Malla, entre otros, incluso sólidos platónicos (Preestablecido, Platónico, Icosaedro por ejemplo). |
|
|
|
|
|
|
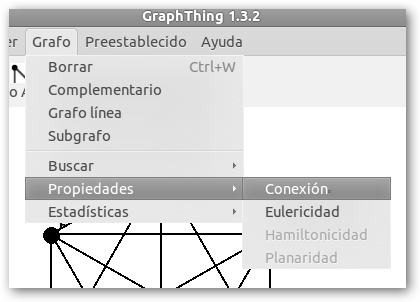
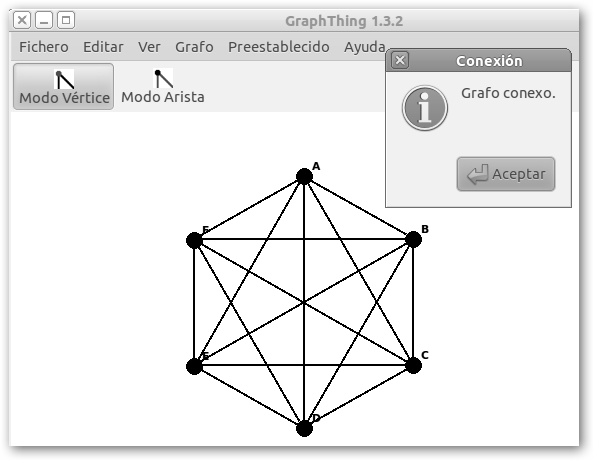
Una vez creado el grafo podemos preguntarle algunas de sus propiedades, por ejemplo, si es conexo, desde Grafo, Propiedades, Conexión. En el ejemplo, el grafo es conexo pues todos sus vértices están conectados, existe siempre un camino desde un vértice a cualquier otro. |
||
|
|
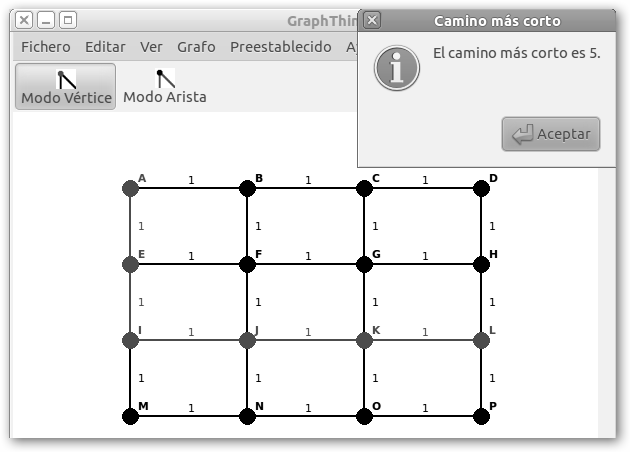
Para ver los pesos del grafo navega por Ver, Pesos. En Modo Vértice selecciona dos vértices manteniendo pulsado la tecla de Mayúsculas de tu teclado. En la entrada de menú Grafo, selecciona la opción Buscar, Camino más corto. En el ejemplo, el camino más corto entre A y L es 5, GraphThing te lo muestra también: AE + EI + IJ + JK +KL. |
|
|
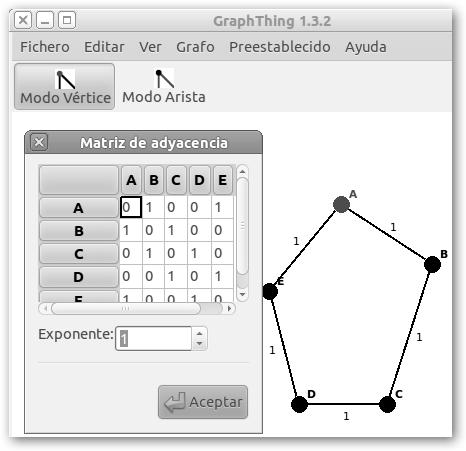
Desde Grafo, Estadísticas, Matriz de adyacencia podemos obtener la matriz de adyacencia. Recuerda que Matriz [Vértice 1, Vértice 2] = 1 si están conectados (por ejemplo: A y E o A y B) y es igual a cero si no lo están (A y C o A y D). Su diámetro
es 2 (Grafo, Estadísticas, Diámetro)
pues para ir de cualquier vértice a otro necesitamos como
máximo un camino de longitud 2 (el del grafo anterior era
6, d(A, P)=6). Matemáticamente, se define:
|
|
|
|
También, podemos calcular el radio de un grafo (Grafo,
Estadísticas, Radio), es decir, el mínimo
de las excentricidades de los vértices de un grafo, donde
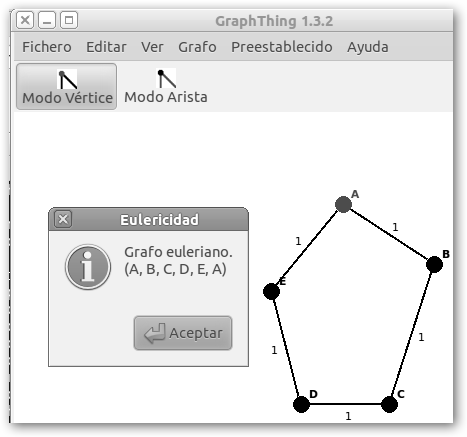
Además, descubrimos que se trata de un grafo euleriano (Grafo, Propiedades, Eulericidad) pues el ciclo A, B, C, D, E y A es un ciclo euleriano, es decir, encuentra un camino (realmente un ciclo) desde A hasta A que pasa por todos los vértices una sola vez. |
|
|
|
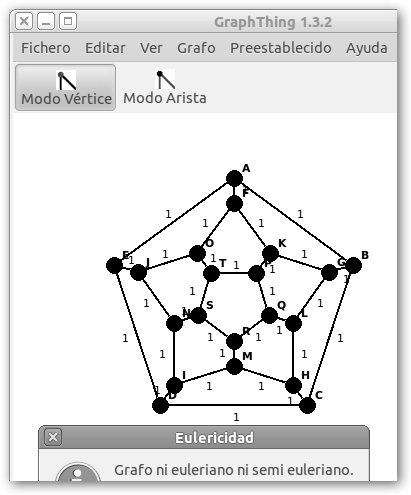
Sin embargo, no siempre las cosas marchan tan bien. En el siguiente ejemplo, el grafo aunque es conexo (Grafo, Propiedades, Conexión) no es euleriano (Grafo, Propiedades, Eulericidad). |
||
|
|
|
|
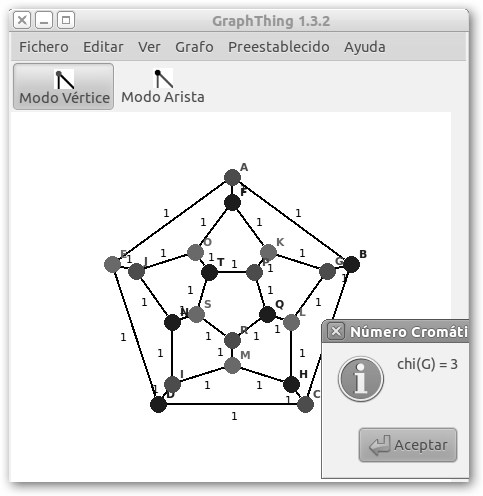
Su número cromático es 3 (Grafo, Estadísticas, Número Cromático) pues el menor número de colores necesarios para pintar el grafo es 3 de suerte que dos vértices que compartan la misma arista tengan siempre distintos colores. El programa muestra incluso los colores, si bien en escala de grises no se aprecia demasiado. Los colores de los vértices son los siguientes: rosa (D, E, K, S, M, L, O), rojo (A, C, G, I, J, P, R y azul (B, D, F, H, N, Q, T). También, podemos calcular el polinomio cromático en Grafo, Estadísticas, Polinomio Cromático y el flujo máximo (Grafo, Buscar, Flujo Máximo) entre dos vértices.
10.3. Planificación de proyectos
La planificación y control de proyectos es una parte importante de la Investigación Operativa que además es utilizado un día sí y otro también en las empresas y organizaciones.
|
|
Existen muchas herramientas libres a tu disposición: * OpenProj: openproj.org. * GanttProject: www.ganttproject.biz. * Planner: live.gnome.org/Planner. * TaskJuggler: http://www.taskjuggler.org/. |
|
|
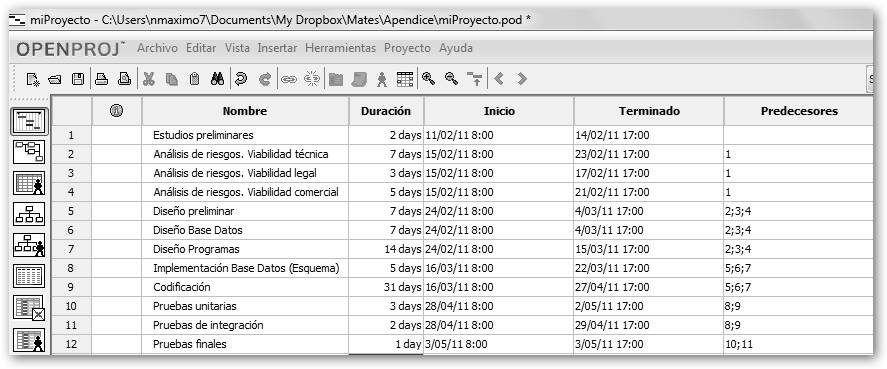
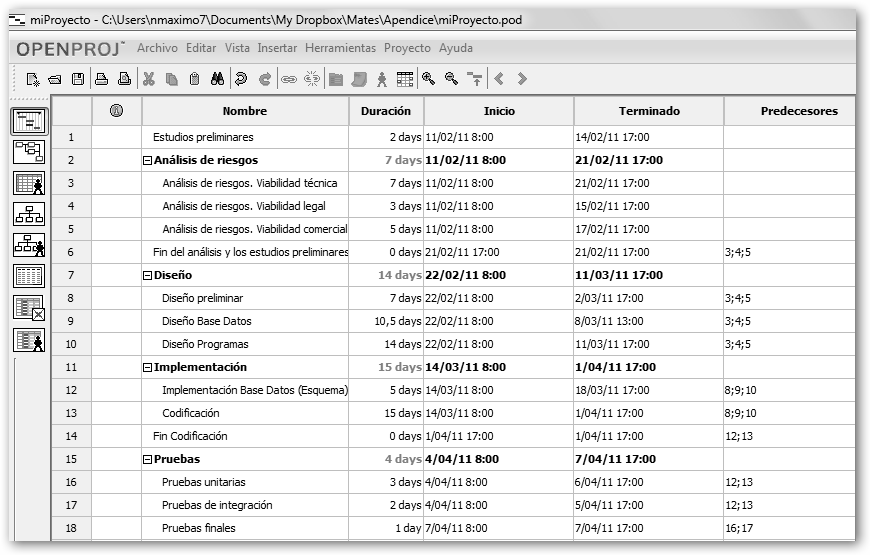
3. El siguiente paso será indicar las tareas en las que se descompone el proyecto: nombre, duración, fecha de inicio, terminado o fecha de fin (la calculará el OpenProj por ti) y predecesores. En el cuadro Predecesores indicarás las tareas que son requeridas para comenzar la que estás definiendo, por ejemplo, la tarea “Diseño preliminar” requiere que la 2, la 3 y la 4 acaben para empezar. |
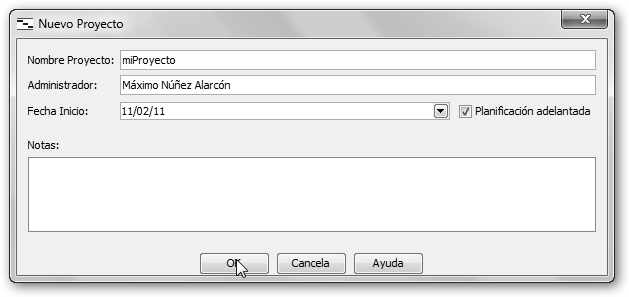
Utilizaremos el primero pero la idea general, el modus operandi es similar entre las aplicaciones. Sigue las siguientes instrucciones: 1. Descarga el programa e instálalo. 2. Al lanzarlo, haz clic en Crea Proyecto. Luego, asígnale un nombre, un administrador, una fecha de inicio y, opcionalmente, puedes teclear notas descriptivas sobre él. |
|
|
¡Fíjate!, las tareas predecesoras están separadas por un punto y coma, en el ejemplo: 2; 3; 4. En Herramientas, Cambia Horario de Trabajo puedes cambiar el calendario por defecto (8 horas a la semana de lunes a viernes).
|
||
|
4. A continuación, definimos los recursos con los que contamos: nombre, tipo (típicamente Trabajo), dirección de correo electrónico, tasa estándar (por ejemplo, 25 euros la hora), etc. |
||
|
Para incluirlos, utilizamos el botón Recursos en el
cuadro lateral izquierdo. 5..
Proseguimos asignando los recursos que tenemos disponibles
(empleados -Trabajo-, equipos, suministros, etc. -Material-) a
las tareas pulsando en el botón Gantt
En la pestaña Predecesores indicamos las tareas que le preceden y el tipo de relación: * FS: por defecto, hasta que no acabe la predecesora, no puede comenzar la tarea. * FF: cuando acabe la predecesora, la sucesora debe finalizar también. * SS: cuando comience la predecesora, la sucesora debe empezar también. * SF: cuando comience la predecesora, la sucesora debe acabar. |
En la pestaña Advanced podemos definir una tarea como un hito (“milestone”) tarea de duración cero que simboliza la consecución de un objetivo del proyecto, así como, limitaciones o restricciones a una tarea en Tipo de Contención: Tan pronto/tarde como sea posible, Debe empezar/terminar ya, etc. |
|
|
Observa el resultado final, todas las tareas están ahora perfectamente definidas. |
||
|
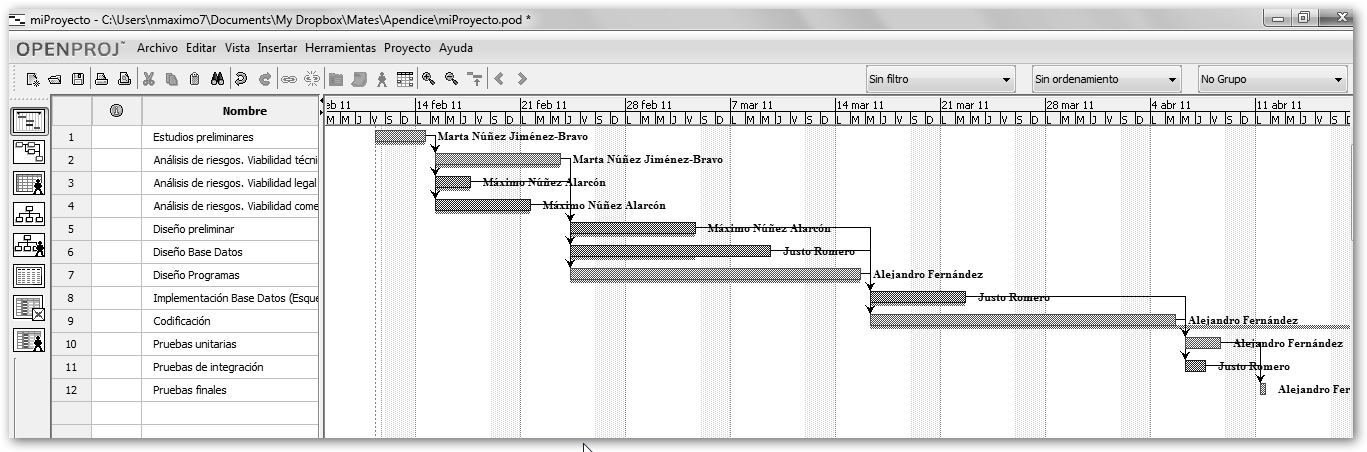
6. A la derecha de las tareas, se encuentra el diagrama de Gantt que OpenProj crea “sobre la marcha”. 7. Haciendo clic en el botón
Red 8.
Los dos botones siguientes de la barra lateral izquierda nos
permiten obtener: la estructura o red de descomposición de
trabajos (WBS) y … |
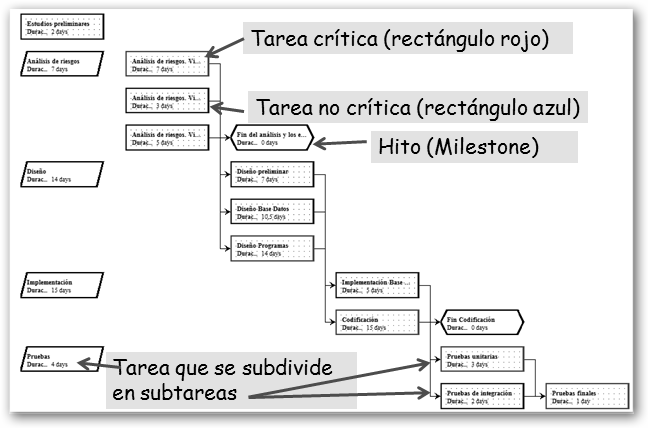
En rojo se muestran las tareas críticas, es decir, las pertenecientes al camino crítico que tienen holgura cero (holgura: Barra de estilos, Total tiempo ocioso), en azul las demás. Las dependencias se visualizan mediante flechas. |
|
|
Detalle en la ilustración superior de la Red PERT del ejemplo “modificado” (léase más abajo) y en la inferior del WBS. |
||
|
… la estructura de desglose de recursos (RBS).
También, se ofrece la posibilidad de ver detalles y diagramas de las tareas y del uso de los recursos; muy útil este último para conocer si una persona está ociosa o sobresaturada en un momento dado. |
Sin embargo, para “afinar” el problema, se ha organizado el proyecto en tareas y sub-tareas. ¿Cómo? Crea una tarea “Análisis de riesgos” y, con el menú contextual, Corta y Pega en la segunda posición. Luego, selecciona las tres tareas de análisis de riesgos (viabilidad técnica, legal y comercial) y haciendo clic con el botón derecho selecciona Identado, automáticamente serán subtareas de la tarea que le precede, en el ejemplo, “Análisis de riesgos”. Además, se han creado dos hitos: “Fin del análisis y de los estudios preliminares” y “Fin Codificación”. |
|
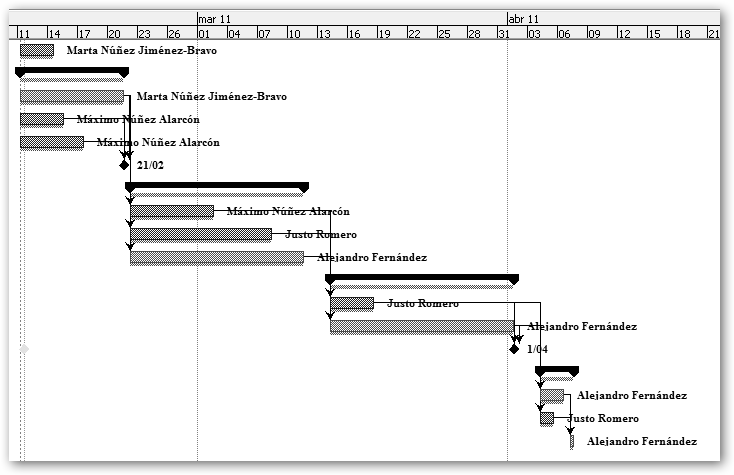
Comprueba en la figura inferior el diagrama GANTT de la versión refinada.
10.4. Programación lineal con GLPK.
Primero, tendremos que instalar el paquete glpk, GNU linear programming kit en Ubuntu, Debian y derivados o navegar a www.gnu.org/software/glpk. A continuación, edita un archivo que llamaremos proglin.mod utilizando el lenguaje de programación GNU MathProg con gedit: gedit proglin.mod.
|
# Ejemplo clásico de programación lineal var x1 >=0; /* Producto A */ var x2 >=0; /* Producto B */ /* Función objetivo */ maximize z: 2*x1 + 4*x2; /* Restricciones */ s.t. Planta1 : x1 <= 4; s.t. Planta2 : x2 <= 4; s.t. Planta3 : x1 +x2 <= 5; end;
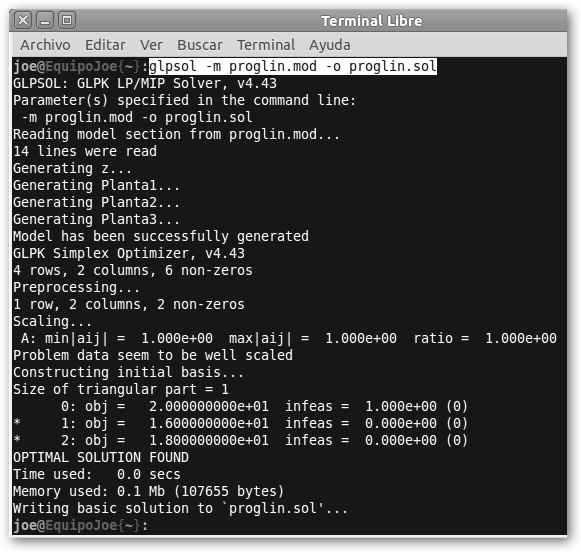
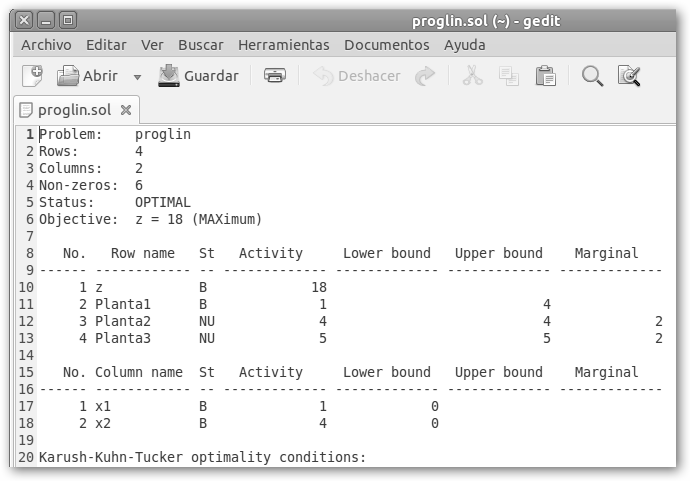
Escribimos el código como se muestra en la figura y ejecutamos la orden en consola: glpsol -m proglin.mod -o proglin.sol. En la figura anterior se observa el resultado de la ejecución. Se ha encontrado una solución óptima. Si editamos la solución que se localiza en el fichero proglin.sol, hallaremos la respuesta a nuestro problema. |
Supongamos que tenemos una fábrica que manufactura dos productos: A y B. El precio del producto A es 2 millones de euros y el del producto B es de 4. Obviamente, ya sabemos lo que queremos: maximizar las ventas por meses, es decir, si x1 es la cantidad de producto A y x2 la cantidad de B sería: 2*x1+4*x2. Sin embargo, tenemos una serie de limitaciones, en particular solo tenemos tres plantas. En las dos primeras, que por supuesto están en China (este dato es muy importante obviamente), los trabajadores están especializados en construir sólo uno de los dos productos y pueden realizar un tope de 4 cada mes. En la primera solo producen el “A” (x1<=4) y en la segunda, el “B” (x2<=4). Estos son las primeras dos restricciones del problema. La tercera restricción se refiere a que en Berlín realizan un testeo de los productos que se fabrican para saber si están conforme a los estándares y normativa europea. Cada mes pueden comprobar un tope de cinco productos pero les es indiferente si son A, B o una combinación de ambos: x1+x2<=5. |
|
|
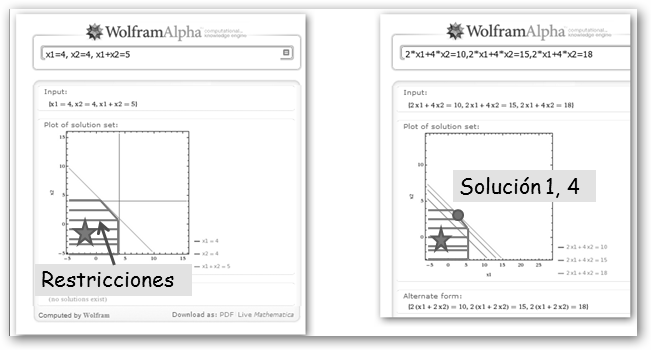
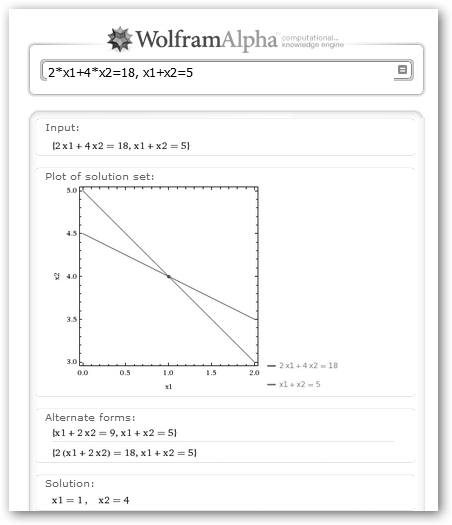
El máximo que podemos obtener con estas restricciones es 18 millones de euros al mes. Además, los valores para x1 y x2 serán 1 y 4 respectivamente, es decir, produciremos 1 del producto “A” y 4 del producto “B”. Observa las representaciones gráficas con WolframAlpha, a la izquierda se muestran las restricciones y el área permitida de valores x1 y x2. Dentro de esta área, solicitamos 2*x1+4*x2=10, 2*x1+4*x2=15 y 2*x1+4*x2=18. El valor máximo lo obtenemos con esta última recta, la más lejana al origen, que toca al área permitida precisamente en (1, 4).
|
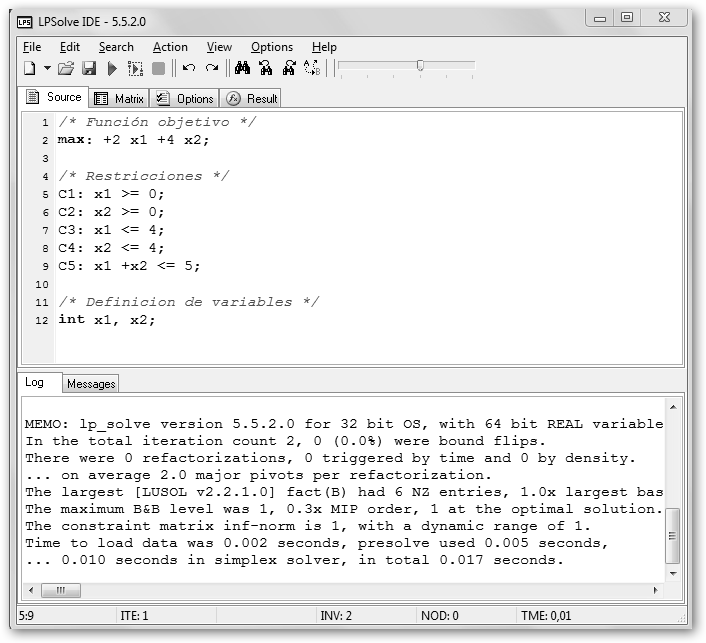
Se observa que este punto es la intersección de las dos rectas: 2*x1+4*x2=18, x1+x2=5. Luego, podemos pedirle a Wolfram que las resuelva algebraicamente y obtenemos de nuevo (1, 4). Si prefieres trabajar en Windows utiliza LPSolveIDE en sourceforge.net/projects/lpsolve/ del proyecto lpsolve.sourceforge.net. Una vez instalado y lanzado, observa en Source el código necesario para resolver el mismo problema anterior. |
|
|
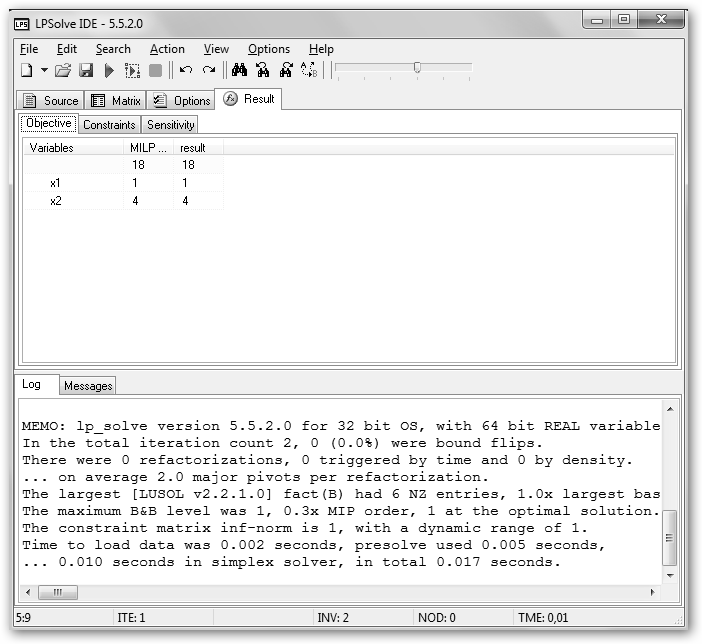
Resuélvelo con el botón Solve (el triangulito verde) o F9 y observa en la pestaña Result, el resultado obtenido. Otra alternativa es Coliop3 en cmpl.th-wildau.de. |
|
10.5. GSL shell: Gráficos 3D, Ajuste no lineal, EDO, etc.
|
Una de las librerías matemáticas “libres”
más importantes actualmente es la GSL, GNU Scientific
Library. Sin embargo, hasta ahora tenías que programar en C
para acceder a ellas y escribir un programa con un buen número
de líneas de código que realizara cualquier tarea
por sencilla que fuera. GSL Shell viene a tu rescate para poder acceder a GSL desde una Shell utilizando el lenguaje Lua que si bien no es Python se le parece bastante. Puedes descargarte la última versión en download.savannah.gnu.org/releases/gsl-shell. Para Ubuntu y Debian ofrecen un paquete .deb con el que instalarlo fácilmente, luego ejecútalo escribiendo en la consola gsl-shell. Existen dos opciones: trabajar interactivamente o escribir nuestros archivos .lua y ejecutarlos, tal como se ve en la ilustración, con dofile(‘MiGsl.lua’). En la figura se muestra cómo se está editando con Geany un archivo MiGsl.lua para graficar la superficie de Klein en paramétricas con surfplot({x=x(u, v), y=y(u, v), z=z(u, v)}, valorMínimoU, valorMínimoV, valorMáximoU, valorMáximoV, {gridu = nºSubdivisionesU, gridv = nºSubdivisionesV, title = título, stroke=false}. Fíjate que necesitas incluir el módulo plot3d: require ‘plot3d’. |
|
También, podemos graficar funciones 3D en cartesianas con plot3d(f(x,y), valorMínimoX, valorMínimoY, valorMáximoX, valorMáximoY, {opciones}). |

|
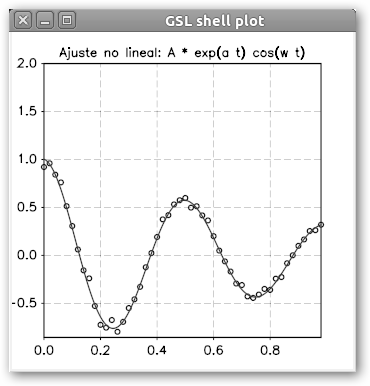
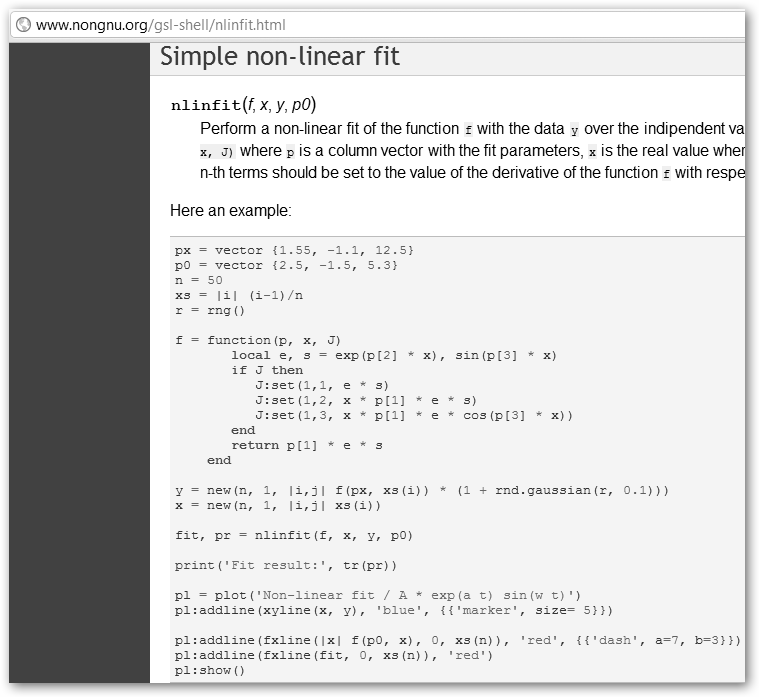
Sin embargo, con GSL podemos crear mucho más que gráficas 3D. GSL incluye primitivas para integración numérica, transformada rápida de Fourier, resolución de EDOs y ajustes no lineales. La documentación la encontrarás en www.nongnu.org/gsl-shell/index.html y un ejemplo de ajuste no lineal se muestra en la figura de la derecha. En la inferior se observa la información que provee al respecto la página Web mencionada anteriormente. La función principal es nlinfit(f, x, y, p0) que realiza un ajuste no lineal de la función “f” (p[1] ep[2]x sin(p[3]x)) con los datos “y” (la propia función más un ruido gaussiano: f(ps, xs(i)) * ( 1 + rnd.gaussian(r, 0.1))) sobre la variable independiente “x” con la semilla inicial “p0”. |
La función f es llamada con f(p, x, J) donde “p” contiene los parámetros de ajuste, “x” los valores en los que debe evaluarse la función y el término enésimo de J es la derivada de f con respecto al parámetro de ajuste enésimo, es decir: “ep[2]x sin(p[3]x)” –p[1]-, “x p[1] ep[2]x sin(p[3]x)” –p[2]- y “x p[1] ep[2]x cos (p[3]x)” –p[3]-. |
|
|
|
Otra alternativa es PyGSL en pygsl.sourceforge.net/reference/pygsl, una interfaz Python a GSL.
10.6. EDO’s y “otras hierbas” con Axiom.
|
Axiom es un proyecto de algebra computacional “libre” que está siendo desarrollado desde 1971. Puedes instalarlo en Windows pero no es un proceso sencillo (visita la página oficial www.axiom-developer.org, en el enlace How to download Axiom?). En Ubuntu basta con escribir sudo apt-get install axiom. En las ilustraciones se muestra Axiom en acción. |
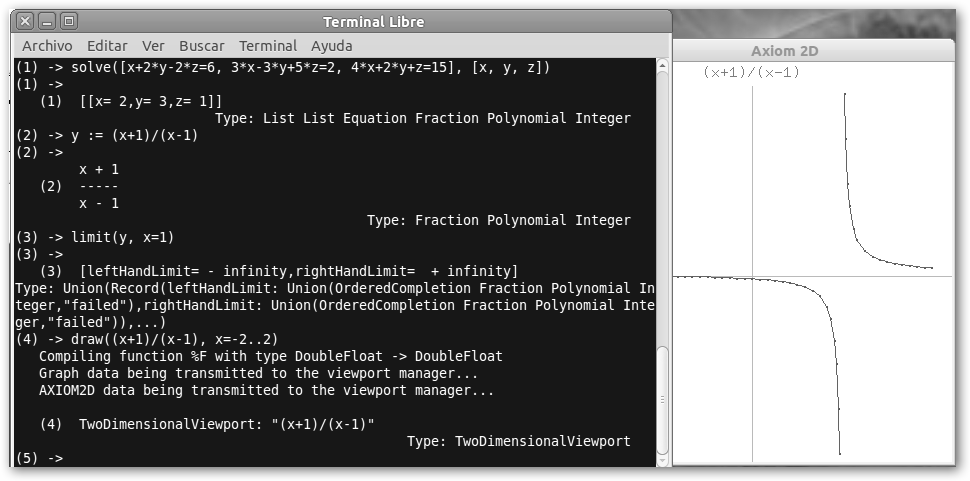
Detalle de la resolución de un sistema de tres ecuaciones con tres incógnitas (solve), el cálculo del límite (limit) y la gráfica de una función 2D (draw). |
|
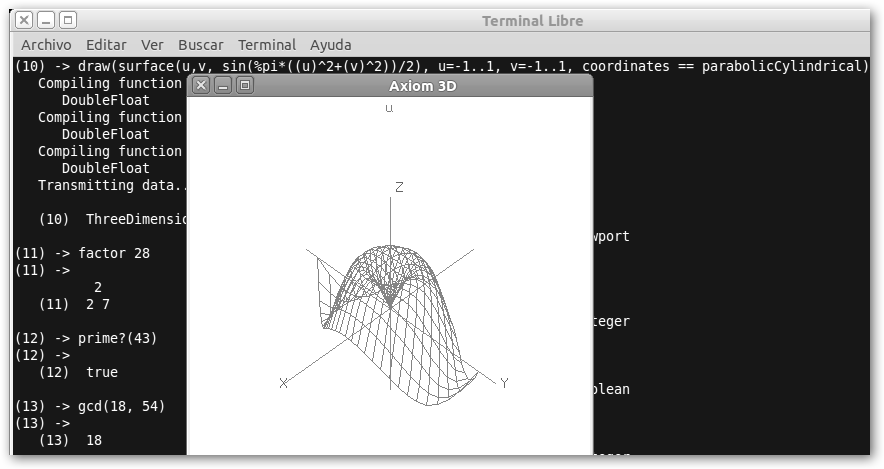
Fíjate cómo hemos dibujado una superficie 3D (draw), solicitado la factorización de un número (factor), preguntado si un número es primo (prime?(43)) y el máximo común divisor de dos números (gcd). Por supuesto, tiene
todas las funciones que podríamos esperar: mínimo común
divisor (lcd), factorial, x**2 (equivale a x2), sin,
cos, tan, asin, acos, atan, min, max, %pi (es Π), %i (es i=
|
La documentación se ofrece tanto en el formato HyperDoc (figura superior) como en la página Web: www.axiom-developer.org, Documentation, fundamentalmente el volumen 1: Axiom Tutorial. |
|
En la documentación se ofrece numerosos ejemplos como los que se muestran en la figura superior para resolver ecuaciones diferenciales ordinarias. |
En la ilustración
se muestra la resolución de
|
10.7. Algebra con Gap.
|
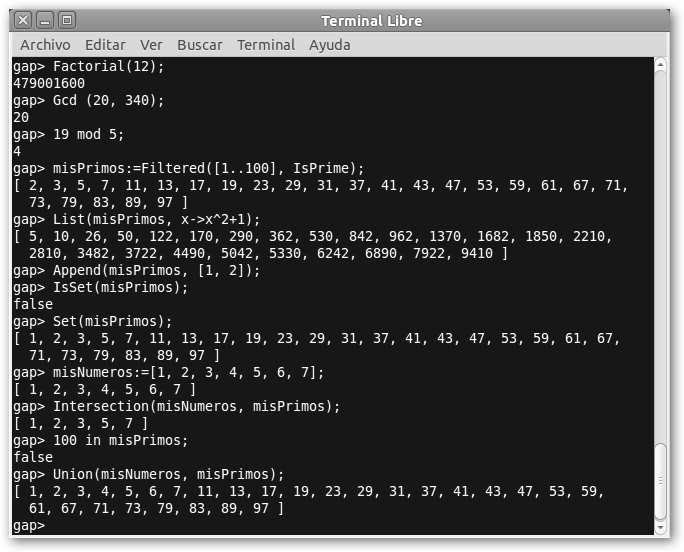
Gap son las siglas de Groups, Algorithms and Programming, es decir, grupos, algoritmos y programación. Se trata de un paquete de software libre, de código abierto y extensible orientado al campo del álgebra abstracta. Podemos realizar operaciones básicas (en la ilustración se observa cómo obtener el factorial -Factorial-, el máximo común divisor -Gcd- y el resto de la división entera -mod-), trabajar con listas y conjuntos. |
misPrimos se obtiene filtrando (Filtered) la secuencia [1..100] con IsPrime, es decir, es la lista de los elementos [1..100] que son primos (si quisieras los pares: misPares := Filtered([1..100], IsEvenInt);). Obtenemos otra lista aplicando sobre misPrimos, la función x2+1 (List (misPrimos, x->x^2+1);) y luego le añadimos (Append) dos elementos: 1, 2. |
|
|
Averiguamos si misPrimos es un conjunto (IsSet(misPrimos); no lo es porque 2 está repetido), lo hacemos un conjunto (Set), creamos otra lista con los números del 1 al 7 (misNumeros) y calculamos la intersección (Intersection) y la unión (Union) entre misPrimos y misNumeros, así como, preguntamos si 100 está en misPrimos (100 in misPrimos). Prueba: Difference([1,2,3],[1,2]); (diferencia de conjuntos, 3), IsSortedList([1,2,3,5,4]); (¿está ordenado la lista [1,2,3,5,4]? False, no) y 3 in misPares; (¿está 3 en misPares? False, no). |
||
|
Resolvamos una ecuación diofántica.
Se trata de una ecuación algebraica cuyas soluciones son números enteros, por ejemplo, 6 x +10 y = 104. |
|
|
|
La ecuación diofántica 6 x +10 y = 104 tiene solución si y solo si miMcd (el máximo común divisor de 6 y 10 –Gcd(6,10)-) es un divisor de 104: 104 mod miMcd da como resultado 0. En tal caso, una solución será los coeficientes de Bézout por el cociente de 104 con el máximo común divisor de 6 y 10: (104/miMcd)* GcdRepresentation(6,10) y obtenemos x=104, y=-52. Finalmente, comprobamos los resultados: last*[6, 10]; equivale a decir [104, -52]*[6, 10]; y tiene que dar 104. |
||
|
Veamos cómo realizar aritmética modular con GAP. Para empezar miAnillo será el anillo Z12. miUno es el elemento neutro para la multiplicación del anillo (miUno:=One(miAnillo)). Podemos realizar cálculos: 2*miUno + 5 * miUno; 3*miUno - 4*miUno; 3*miUno -4/(5*miUno); etc. Recordemos que en
Zn sólo tienen inverso multiplicativo
( ¿Cuáles son todos los números que tienen inverso multiplicativo? PrimeResidues(12); es decir, aquellos elementos menores a 12 que son coprimos con 12. ᵩ(12), es decir, la función de Euler en 12, el número de enteros menores a 12 que son coprimos con 12 (Phi(12);) es el número de elementos en Z12 que tiene inverso multiplicativo. |
¡Prueba!: Size(miAnillo); Size(Integers); devuelven 12 e infinito. |
|
|
Por último: IsField(miAnillo) ¿es cuerpo Z12? No, pues 12 no es primo. En Z13 todos sus elementos son coprimos con 13 y, por tanto, tienen inverso multiplicativo: IsField(ZmodnZ(13)); |
||
|
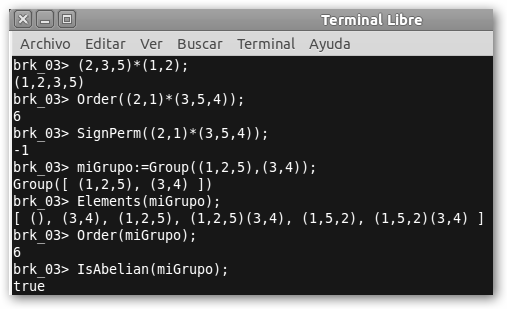
En la siguiente figura se muestra cómo Gap permite trabajar con permutaciones. El operador “*” es la composición: (2,3,5)* (1,2); da (1, 2, 3, 5): 2->3; 3->5; 5->2->1; 1->2; mientras que 2^(2, 3, 4); sería la imagen de 2 por la permutación (2,3,4): 3. Podemos calcular el orden y el signo de las permutaciones con Order y SignPerm. SignPerm((2,1)*(3,5,4)); es -1 pues puede escribirse como un número impar de transposiciones (-1)3=-1: (2,1)*(3,5,4); = (1,2)(3,5,4) =(2,1)*(3,4)*(4,5); Se comprueba que si una permutación es composición de ciclos disjuntos con longitudes l1,…,lm, su orden será el mínimo común múltiplo de dichas longitudes, en este caso, Lcm(2, 3); es 6. |
Comprueba que el conjunto Sn de las permutaciones de {1,…n} con la composición es un grupo (el grupo simétrico) no conmutativo: (2,3,5)*(1,2)(4,5); es (1,2,3,4,5). Sin, embargo, (1,2)(4,5)*(2,3,5); da (1,3,5,4,2). |
|
|
A continuación, se ha definido el grupo formado por las permutaciones (1,2,5) y (3,4), y se ha solicitado sus elementos, su orden y preguntado si es abeliano. |
||
|
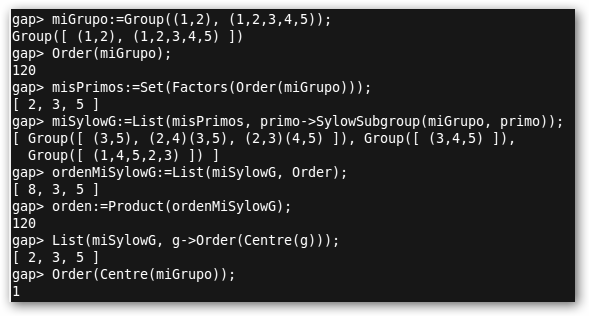
Se crea otro grupo formado por las permutaciones (1,2) y (1,2,3,4,5). Calculamos su orden (120=23*3*5) y la lista “misPrimos” de sus factores (2, 3 y 5). Obtenemos la lista de los p-subgrupos de miGrupo a partir de dichos factores: miSylowG:=List(misPrimos, primo-> SylowSubgroup(miGrupo, primo)); Recuerda la definición: si |G|=prm con m y p coprimos, un subgrupo S de G es un p-subgrupo de Sylow si |S|=pr. |
Si quieres ayuda, por ejemplo, de SylowSubgroup teclea: ?SylowSubgroup. |
|
|
También, solicitamos la lista de los órdenes de dichos subgrupos: ordenMiSylowG:= List(miSylowG, Order); que no son más que las potencias de los factores que dividen al orden del grupo: 23, 3 y 5 y su producto es el orden del grupo (orden:= Product(ordenMiSylowG);). Además, corroboramos que los p-subgrupos tienen centro no trivial: List(miSylowG, g->Order(Centre(g)));. |
||





 paréntesis
necesitamos el teclado en castellano.
paréntesis
necesitamos el teclado en castellano.





 del cuadro lateral izquierdo.
del cuadro lateral izquierdo.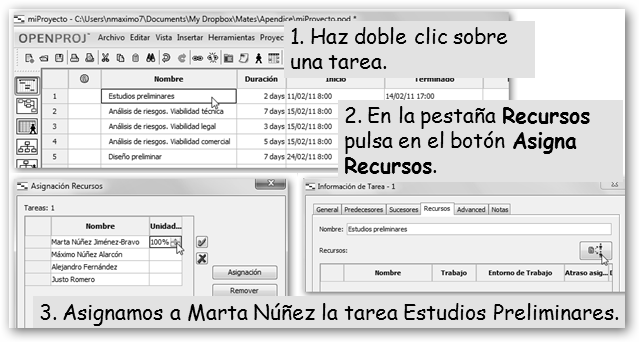

 de la barra lateral izquierda obtenemos la Red PERT.
de la barra lateral izquierda obtenemos la Red PERT. 

 ¡Eso se acabó!
¡Eso se acabó!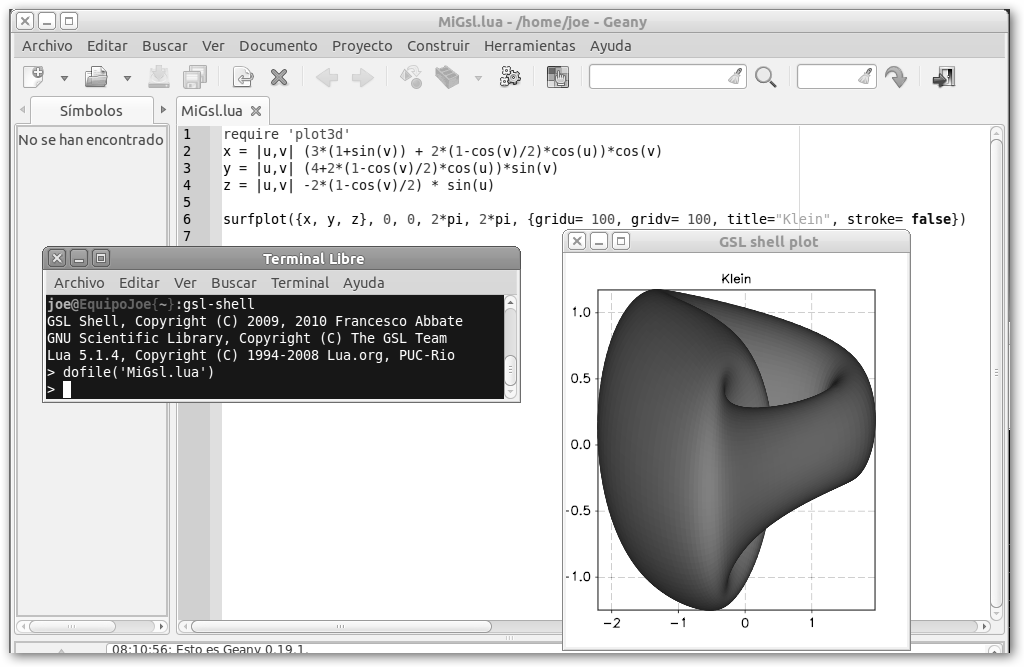



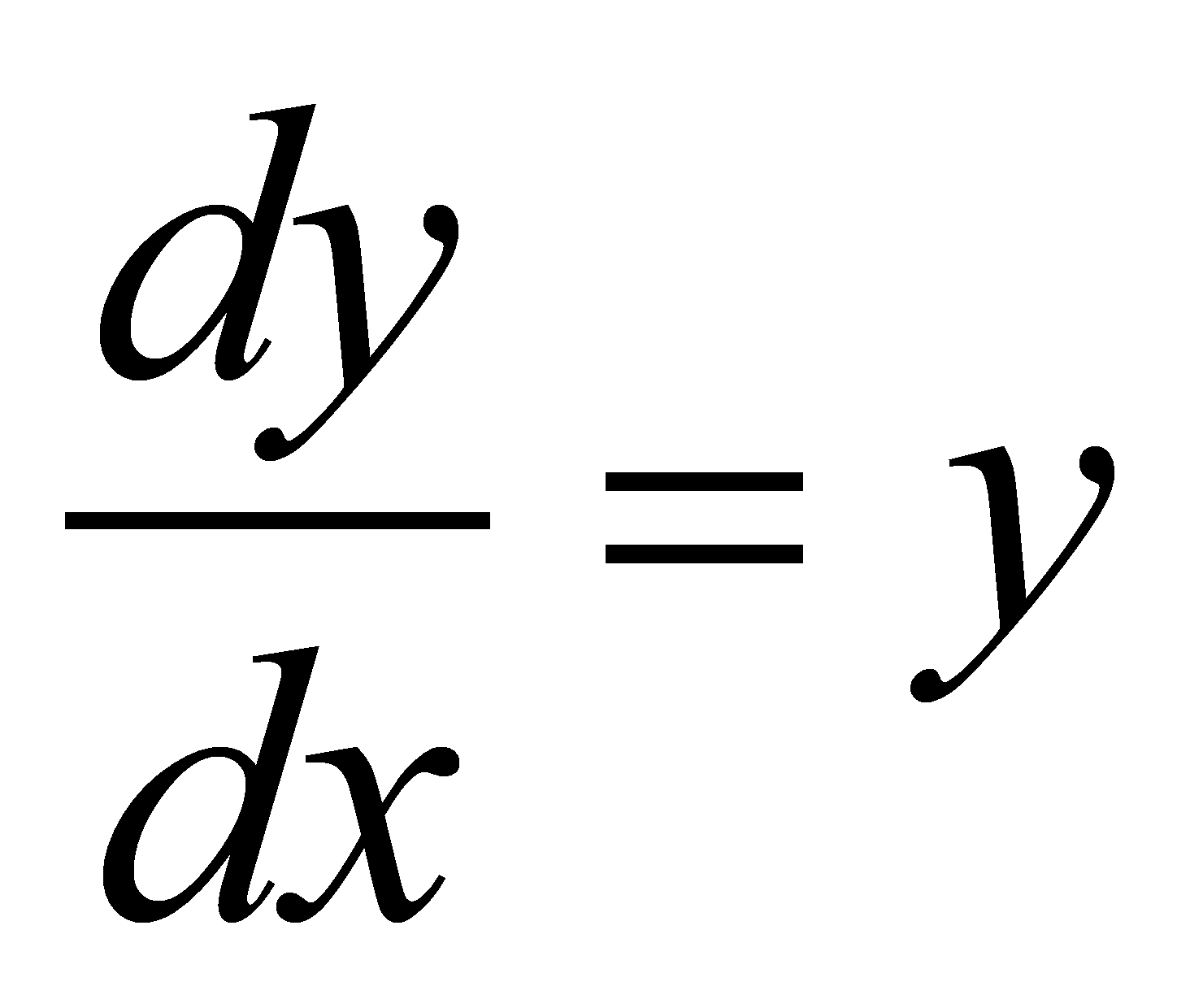 , así como,
, así como,
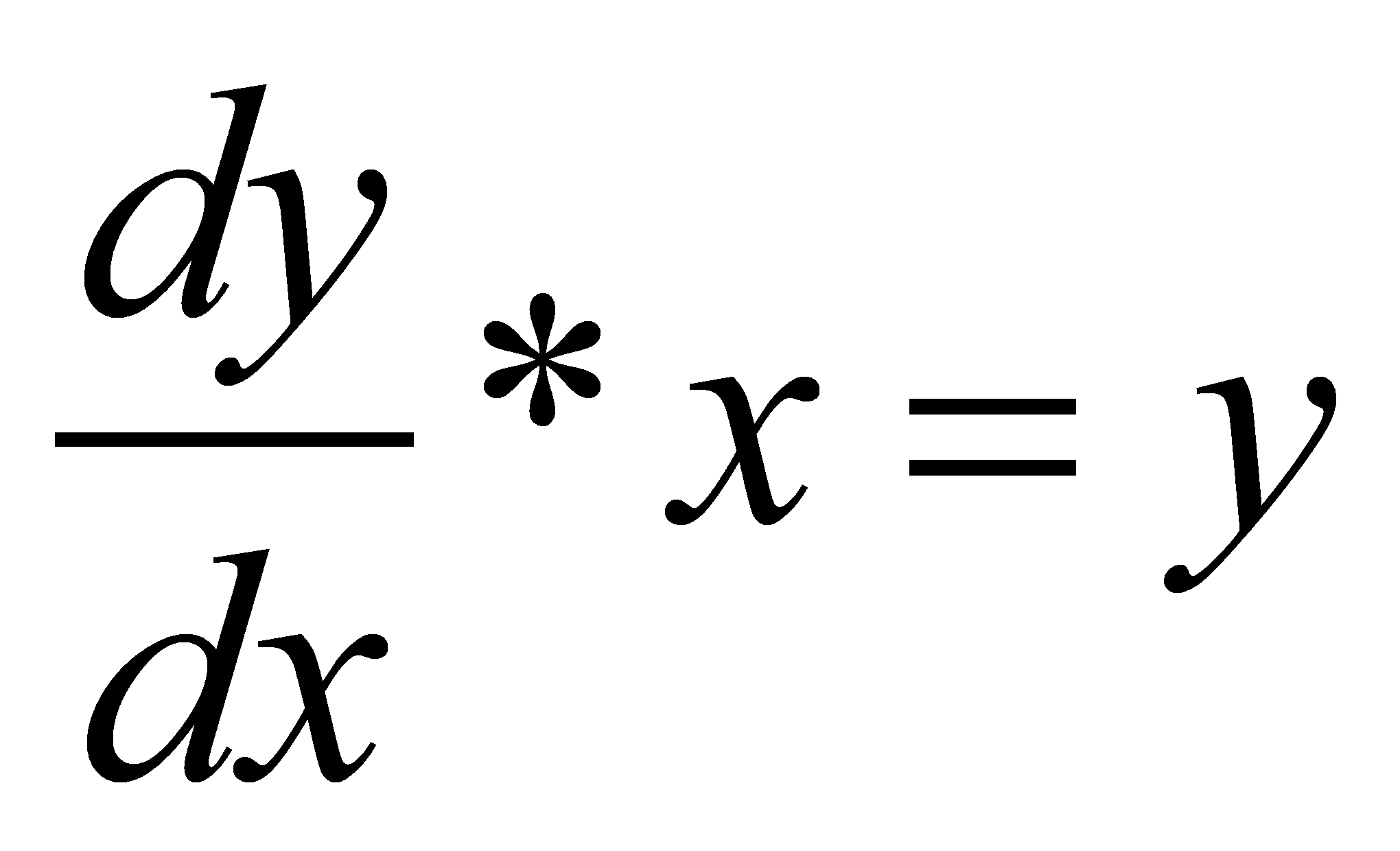 para las condiciones iniciales (0, 1): ex y (0,0),
(1,2) respectivamente: 0 y 2x. Sin embargo, te advierto: ¡No
esperes milagros en la resolución de EDOs en ningún CAS libre!
para las condiciones iniciales (0, 1): ex y (0,0),
(1,2) respectivamente: 0 y 2x. Sin embargo, te advierto: ¡No
esperes milagros en la resolución de EDOs en ningún CAS libre!